Сибирева А.Р. Высшая математика для студентов технических специальностей в формулах и таблицах
Подождите немного. Документ загружается.

21
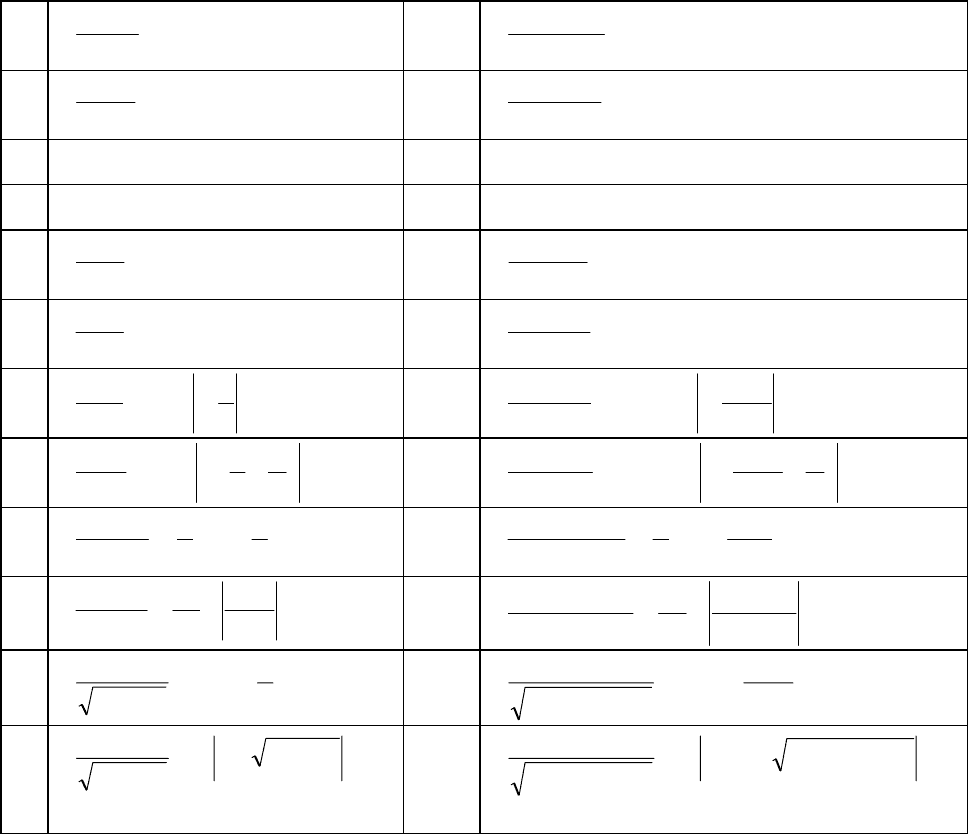
7.
∫
+= Ctgxdx
x
cos
2
1
7.*
∫
+= C)x(tgu)x(du
)x(ucos
2
1
8.
∫
+−= Cxctgdx
x
sin
1
2
8.*
∫
+−= C)x(uctg)x(du
)x(usin
1
2
9.
∫
+= Cxchdxxsh
9.*
∫
+= C)x(uch)x(du)x(ush
10.
∫
+= Cxshdxxch
10.*
∫
+= Cxushxduxuch )( )()(
11.
∫
+= Cxthdx
x
ch
1
2
11.*
∫
+= Cxuthxdu
xuch
)( )(
)(
1
2
12.
∫
+−= Cxcthdx
x
sh
1
2
12.*
∫
+−= C)x(ucth)x(du
)x(ush
1
2
13.
∫
+= C
x
tglndx
xsin
2
1
13.*
∫
+= C
)x(u
tgln)x(du
)x(usin
2
1
14.
∫
++= C)
x
(tglndx
xcos
42
1
π
14.*
∫
++= C)
)x(u
(tgln)x(du
)x(ucos
42
1
π
15.
∫
+=
+
C
a
x
arctg
a
x
a
dx
1
22
15.*
∫
+=
+
C
a
xu
arctg
axua
xdu
)(1
))((
)(
22
16.
∫
+
+
−
=
−
C
ax
ax
ln
a
ax
dx
2
1
22
16.*
∫
+
+
−
=
−
C
a)x(u
a)x(u
ln
a
a))x(u(
)x(du
2
1
22
17.
∫
+=
−
C
a
x
arcsin
xa
dx
22
17.*
∫
+=
−
C
a
)x(u
arcsin
))x(u(a
)x(du
22
18.
∫
+±+=
±
Caxxln
ax
dx
22
22
18.*
∫
+±+=
±
Ca))x(u()x(uln
a))x(u(
)x(du
22
22
В этих формулах a – постоянная,
x
- независимая переменная,
)(xu
–
любая дифференцируемая функция от независимой переменной
x
.
Замечание. Справедливость формул интегрирования, а также каждый
результат интегрирования можно проверить путем дифференцирования, так
как интегрирование есть действие обратное дифференцированию.
5.4. Определенный интеграл
Пусть функция
)x(f определена на отрезке ]b,a[ . Если
1) разделить отрезок произвольным способом на n частичных отрезков дли-
ною
,,...,,,
321 n
xxxx ∆∆∆∆
2) выбрать в каждом частичном отрезке по одной произвольной точке
ξ
1
,ξ
2
,ξ
3
,..., ξ
n
,
3) вычислить значение функции
)(xf в выбранных точках,
4) составить сумму
∑
=
∆=∆++∆+∆+∆
n
i
iinn
x)(fx)(f...x)(fx)(fx)(f
1
332211
ξξξξξ
,
то она называется интегральной суммой функции
)x(f на отрезке ]b,a[ .
22
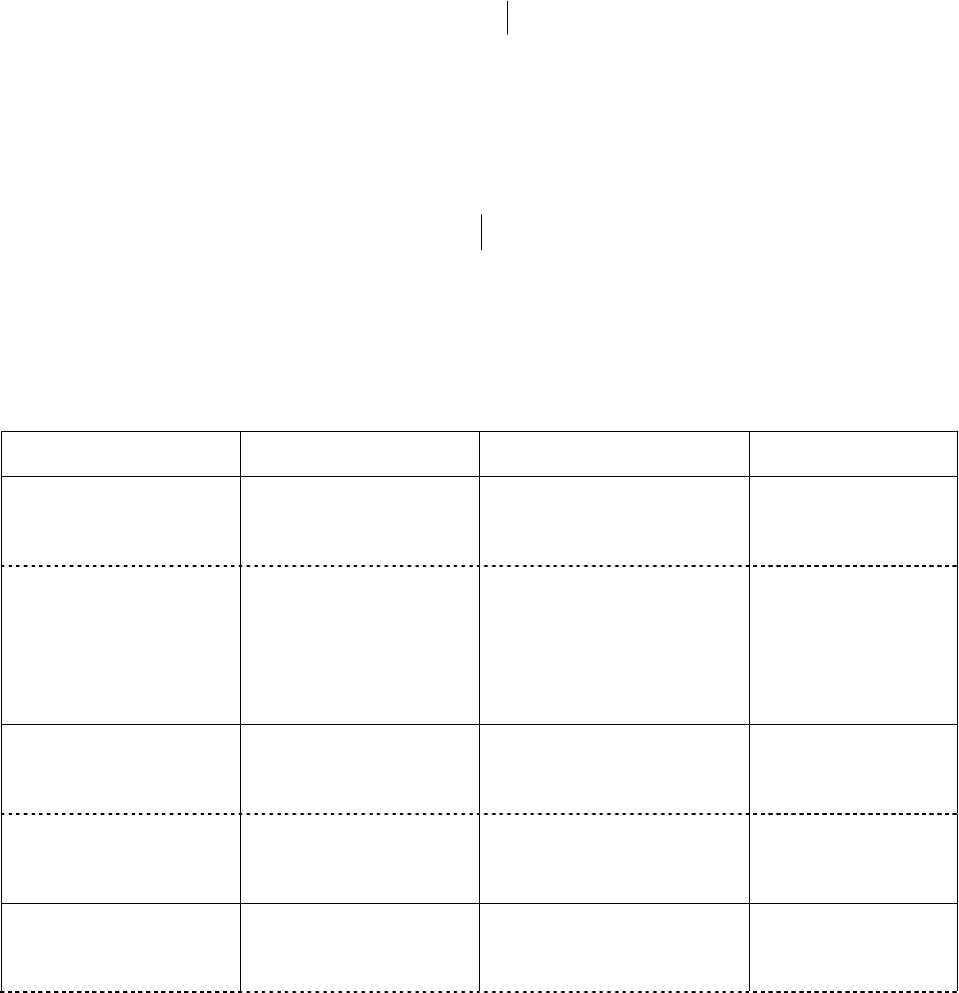
Определение. Предел интегральных сумм
∑
=
∆
n
i
ii
x)(f
1
ξ
функции
)x(fy
=
на отрезке
]b,a[
при 0max →∆
i
x , если он существует, конечен, не зависит от
способа разбиения
]b,a[
на части и выбора точек
i
ξ
,
называют определенным интегралом функции
)x(f
на отрезке
]b,a[
и обо-
значают
⎟
⎠
⎞
⎜
⎝
⎛
∆=
∑
∫
=
→∆
n
i
ii
xmax
b
a
x)(flimdx)x(f
i
1
0
ξ
.
Для вычисления определенного интеграла в случае, когда можно най-
ти соответствующий неопределенный интеграл, служит формула Ньютона-
Лейбница
5.5. Интегрирование по частям
Формула интегрирования по частям имеет вид
∫
∫
−= duuud vvv .
Для определенного интеграла
∫∫
−=
b
a
b
a
b
a
duuud vvv
.
Применение формулы интегрирования по частям целесообразно в тех
случаях, когда последний интеграл будет проще исходного или когда он бу-
дет ему подобен.
Таблица типичных интегралов,
к которым применима формула интегрирования по частям.
∫
vud
u vd
∫
xdxsinx
x
x dxsin
∫
xdxcosx
x
dxxcos
∫
xdxsin)x(P
n
)x(P
n
dxxsin
∫
xdxcos)x(P
n
(где
)(xP
n
- много-
член степени
n )
)x(P
n
dxxcos
Применить
формулу
n раз
∫
⋅ dxex
x
x
dxe
x
∫
⋅ dxax
x
x
dxa
x
∫
⋅ dxe)x(P
x
n
)x(P
n
dxe
x
∫
⋅ dxa)x(P
x
n
)x(P
n
dxa
x
Применить
формулу
n
раз
∫
xdxln
xln dx
∫
xdxlog
a
xlog
a
dx
).a(F)b(F)x(Fdx)x(f
b
a
b
a
−==
∫

23
∫
⋅ xdxln)x(P
n
xln
dx)x(P
n
∫
⋅ xdxlog)x(P
an
xlog
a
dx)x(P
n
∫
dxxarctg
x
arctg
dx
( arcctg x ,
xarcsin
,
xarccos )
(
x
arcct
g
,
x
arcsin
xarccos )
∫
dx(x)arctg xP
n
x
arctg
dx)x(P
n
∫
xdx(x)arcctg P
n
arcctg x
dx)x(P
n
∫
dxbxsine
ax
∫
dxbxcose
ax
ax
e (или
bxsin
)
ax
e (или bxcos )
dxbxsin
(или dxe
ax
)
dxbxcos (или dxe
ax
)
Применить
формулу 2 раза
5.6. Интегрирование дробно-рациональных выражений
Рассмотрим интеграл от дробно-рациональной функции
dx
xQ
xP
m
n
∫
)(
)(
, где
)(xP
n
- многочлен степени n , )(xQ
m
–многочлен степени m .
Для нахождения интеграла
1) если
mn ≥
, разделим )(xP
n
на )(xQ
m
. Представим подынтегральную функ-
цию в виде суммы многочлена и правильной рациональной дроби
)(
)(
xQ
xR
, у
которой степень числителя ниже степени знаменателя.
2) Разложить знаменатель
)(xQ
на простейшие действительные множители.
В общем случае, согласно основной теореме алгебры, это разложение мо-
жет содержать линейные и квадратичные множители
rhkl
)dcxx...()qpxx()bx...()ax(a)x(Q ++++−−=
22
0
,
где квадратичные множители не имеют действительных корней.
3) Написать схему разложения дроби на элементарные слагаемые дроби в
следующем виде
++
−
++
−
+
−
++
−
++
−
+
−
= ...
)bx(
B
...
)bx(
B
bx
B
...
)ax(
A
...
)ax(
A
ax
A
)x(Q
)x(R
k
k
l
l
2
21
2
21
++
++
+
++
++
+
+
++
+
+ ...
)qpxx(
NxM
...
)qpxx(
NxM
qpxx
NxM
h
hh
222
22
2
11
r
rr
dcxx
DxC
dcxx
DxC
dcxx
DxC
)(
...
)(
222
22
2
11
++
+
++
++
+
+
++
+
+ . (*)
4) Освободиться от знаменателей, умножая обе части равенства (*) на
)(xQ .
5) Два многочлена равны, если равны коэффициенты при одинаковых степе-
нях
x
. Составить систему уравнений, приравнивая коэффициенты при
одинаковых степенях х.
6) Решить систему уравнений, найти A
1
,...,A
l
; B
1
,...,B
k
;...;C
1
,D
1
,...,C
r
,D
r
.
7) Подставить найденные значения A
1
,...,A
l
; B
1
,...,B
k
;...;C
1
,D
1
,...,C
r
,D
r
в выра-
жение (*).
8) Найти интегралы от целой части дроби и суммы элементарных дробей.
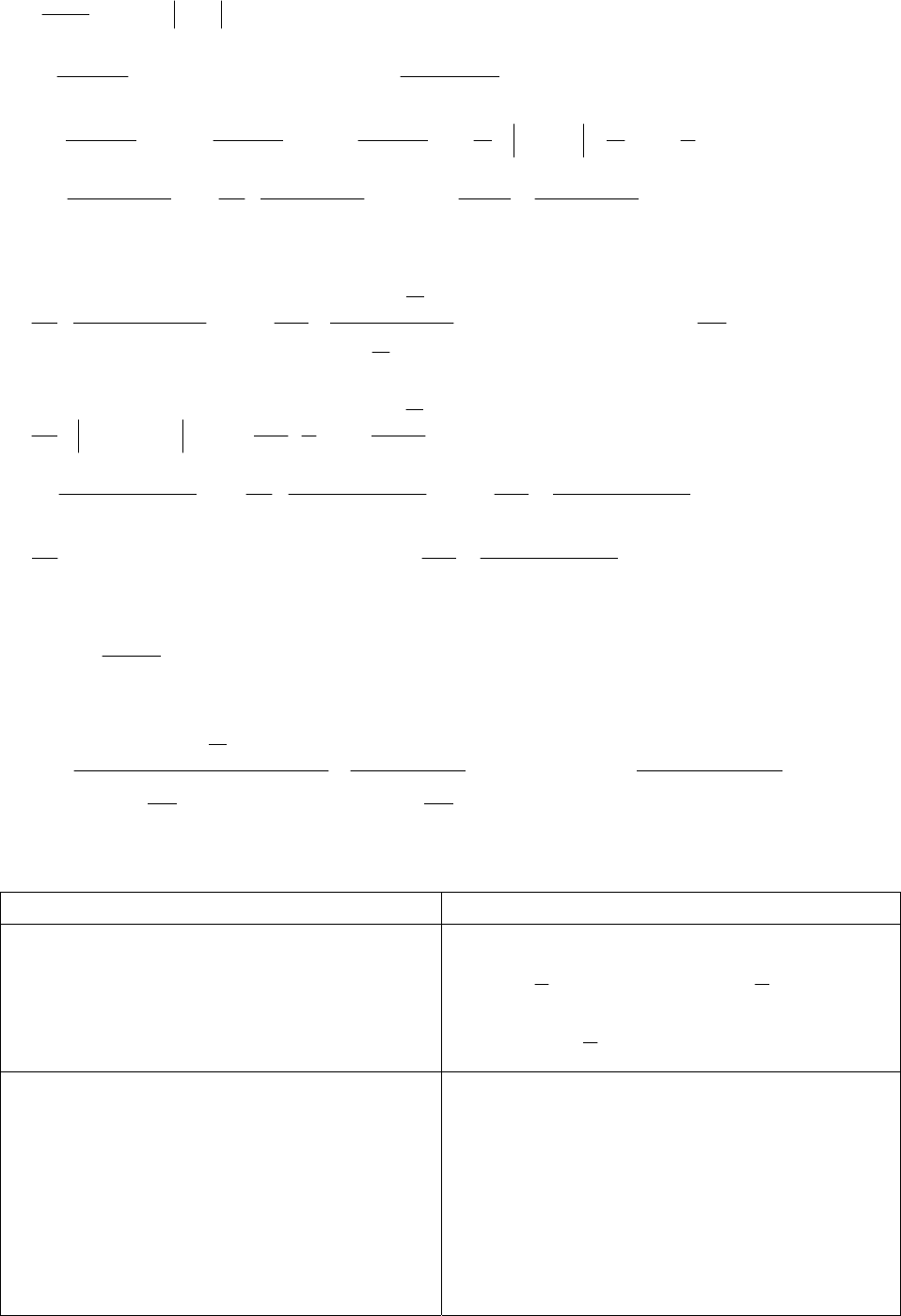
24
Интегрирование элементарных дробей
I.
∫
+−=
−
CaxlnAdx
ax
A
.
II.
()
∫∫
+
+−
−
=−−=
−
+−
−
C
n
)ax(
A)ax(d)ax(Adx
ax
A
n
n
n
1
1
)1(
≠
n .
III.
∫∫∫
+++=
+
+
+
=
+
+
C
a
x
arctg
a
B
axln
A
dx
a
x
Bdx
a
x
x
Adx
a
x
BAx
22
222222
2
1
.
IV.
∫∫ ∫
=
++
⋅
−+
++
+
=
++
+
dx
qpxx
dx
)
pM
N(dx
qpxx
pxM
dx
qpxx
NMx
222
2
2
2
Многочлен
qpxx ++
2
не имеет действительных корней, т.е. 04
2
<− qp .
∫∫
=
++
+
−+
++
++
=
22
2
2
)
2
(
)
2
(
)
2
(
)(
2
a
p
x
p
xd
Mp
N
qpxx
qpxxdM
)0
4
(
2
2
>−=
p
qa
a
p
x
arctg
a
)
Mp
N(qpxxln
M
2
1
22
2
+
−+++=
.
V.
∫∫∫
=
++
−+
++
+
=
++
+
nnn
)qpxx(
dx
)
Mp
N(
)qpxx(
pxM
dx
)qpxx(
NMx
222
2
2
2
∫∫
++
−+++++=
−
.
)qpxx(
dx
)
Mp
N()qpxx(d)qpxx(
M
n
n
2
22
22
Первый интеграл в правой части равенства – интеграл вида
C
n
u
duu
n
n
+
+−
=
+−
−
∫
1
1
, где qpxxu ++=
2
.
Ко второму интегралу применим рекуррентную формулу
m
m
m
I
)
p
q(m
m
)qpxx)(
p
q(m
p
x
I
4
2
12
4
2
2
2
2
2
1
−
−
+
++−
+
=
+
, где
∫
+
+
++
=
12
1
)(
m
m
qpxx
dx
I
.
В нашем случае nm =
+
1 , т.е. 1
−
=
nm .
5.7. Интегрирование тригонометрических выражений
Вид интеграла Способ интегрирования
∫
dxxcosxsin
mn
,
где
n и m – четные
Используем формулы
)cos(sin
αα
21
2
1
2
−= , )cos(cos
αα
21
2
1
2
+= ,
ααα
2
2
1
sincossin =⋅
∫
dxxcosxsin
mn
,
где
n , m –нечетные (оба числа или
одно из них нечетное)
От нечетной степени отделить один
множитель, ко-функцию к отделенно-
му множителю записать под знаком
дифференциала.
Воспользоваться тождеством
1
22
=+ xcosxsin ,
добиться, чтобы в подынтегральном
выражении фигурировала лишь функ-

25
ция, стоящая под знаком дифферен-
циала. Подстановка:
x
cost = (
x
sint
=
).
∫
xdxtg
n
Подстановка
t
x
tg
=
, tarctg
x
=
,
dt
t
dx
2
1
1
+
=
∫
xdxctg
n
Подстановка
t
x
ct
g
=
∫
⋅ dxbxcosaxsin
∫
⋅ dxbxsinaxsin
∫
⋅ dxbxcosaxcos
Используем формулы
],x)basin(x)ba[sin(bxcosaxsin −++=⋅
2
1
],x)bacos(x)ba[cos(bxsinaxsin +−−=⋅
2
1
]x)bacos(x)ba[cos(bxcosaxcos −++=⋅
2
1
.
∫
dx)xcos,x(sinR
,
где
)xcos,x(sinR – рациональная
функция, зависящая от
x
cos,
x
sin
Универсальная подстановка
t
x
tg =
2
,
2
1
2
t
t
xsin
+
= ,
2
2
1
1
t
t
xcos
+
−
=
,
tarctgx 2
⋅
=
,
2
1
2
t
dt
dx
+
⋅
=
∫
dx)xcos,x(sinR
,
где
)xcos,x(sinR)xcos,xsin(R
−
=−
Подстановка
t
x
cos
=
,
2
1 txsin −=
,
tarccos
x
=
,
2
1 t
dx
dx
−
−=
∫
dxxxR )cos,(sin
,
где
)xcos,x(sinR)xcos,x(sinR
−
=−
Подстановка
t
x
sin
=
,
2
1 txcos −=
,
tarcsin
x
=
,
2
1 t
dx
dx
−
=
∫
dx)xcos,x(sinR
,
где
)xcos,x(sinR)xcos,xsin(R
=
−−
Подстановка
t
x
t
g
=
,
2
1 t
t
xsin
+
=
,
2
1
1
t
xcos
+
=
, tarctg
x
=
,
2
1 t
dx
dx
+
=
5.8. Метод подстановки. Метод подстановки, или замены переменной, со-
стоит в том, что при вычислении интеграла
∫
dx)x(f вместо переменной
x
вводится новая переменная
t , связанная с
x
определенной зависимостью
)t(x
ϕ
= , где )t(
ϕ
монотонна и дифференцируема. При этом функцию )t(
ϕ
следует выбирать так, чтобы подынтегральная функция становилась более
удобной для интегрирования
∫
∫
′
=
dt)t()]t([fdx)x(f
ϕϕ
.
Чтобы после интегрирования возвратиться к прежней переменной
x
,
достаточно в полученной функции заменить
t значением, которое находится
из соотношения
)t(x
ϕ
=
, т.е. значением
)x(t
ψ
=
, где
)x(
ψ
обратная функция
для
)t(
ϕ
.
Для определенного интеграла
∫∫
′
=
2
1
t
t
b
a
dt)t()]t([fdx)x(f
ϕϕ
, где )a(t
ψ
=
1
, )b(t
ψ
=
2
.
26
Интегрирование некоторых иррациональных выражений
Вид интеграла Подстановка
∫
dxxxxR
s
r
q
p
n
m
),...,,(
µ
xt = , где ),...,,( sgnНОК
=
µ
,
µ
tx = , dttdx
1−
⋅=
µ
µ
∫
+
+
+
+
dx
dcx
bax
dcx
bax
xR
s
r
n
m
))(,...,)(,(
µ
dcx
bax
t
+
+
=
, где ),...,,( sgnНОК
=
µ
Тригонометрические подстановки
1)
∫
− dxxaxR ),(
22
tsina
x
⋅
=
,
a
x
arcsint
= ,
tcosatsinaaxa ⋅=−=−
22222
,
dttcosadx
=
2)
∫
+ dxxaxR ),(
22
tt
g
a
x
⋅
=
,
a
x
arctgt
= ,
tcos
a
ttgaaxa
=+=+
22222
,
dt
tcos
a
dx
2
=
3)
∫
− dxaxxR ),(
22
tcos
a
x
= ,
x
a
arccost
= ,
ttgaa
tcos
a
ax
2
2
2
22
⋅=−=− ,
dt
tcos
tsina
dx
2
=
R
– рациональная функция от соответствующих выражений.
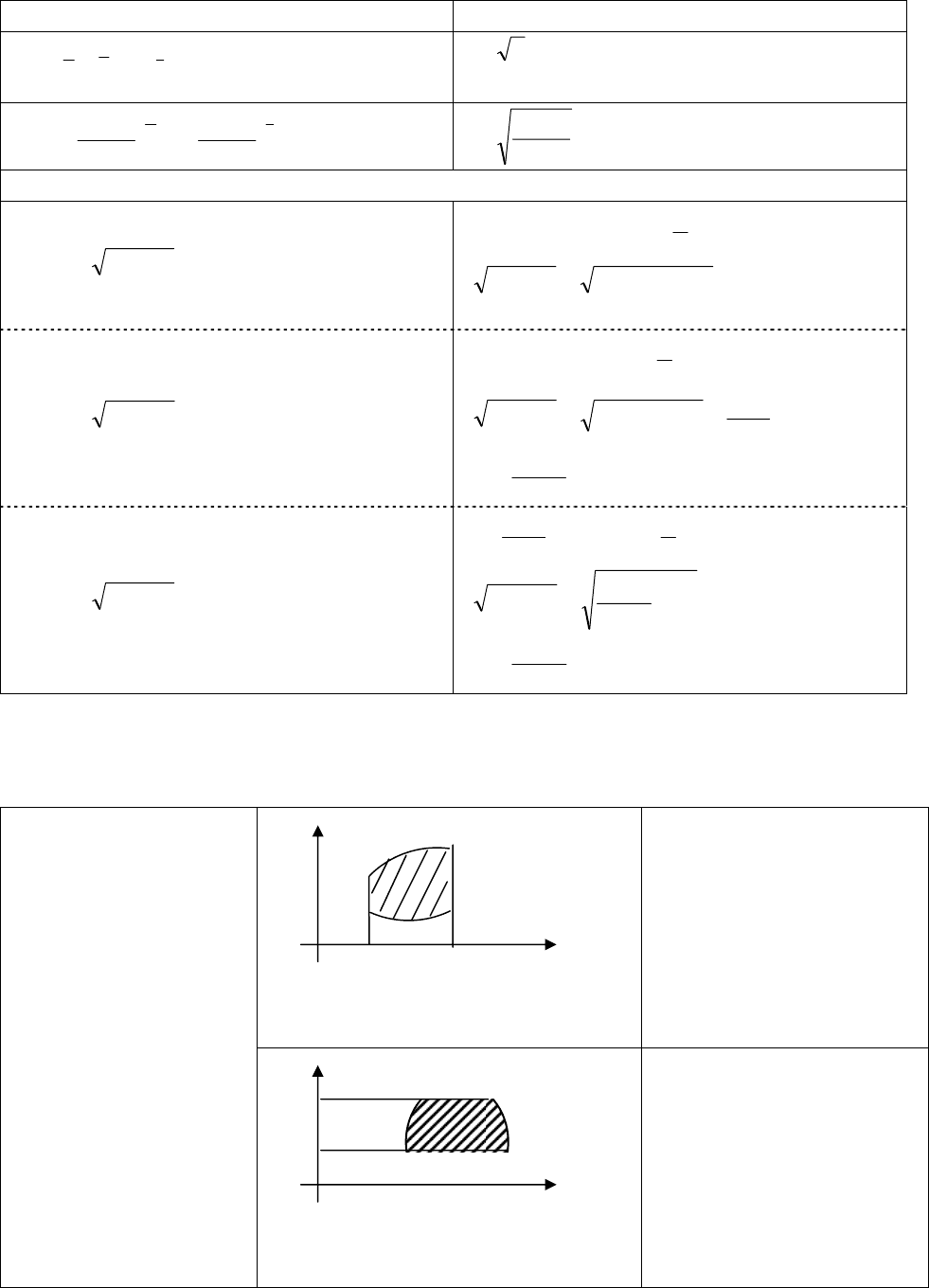
5.9.Геометрические приложения определенного интеграла
Площадь в декарто-
вых координатах
)(xfy = , )(xgy
=
– непрерывны,
)()( xgxf ≥ , ];[ bax
∈
∫
−=
b
a
dxxgxfS ))()((
)( yx
ϕ
= , )( yx
ψ
=
– непрерывны,
)y()y(
ψ
ϕ
≤ , ];[ dcy
∈
∫
−=
d
c
dy))y()y((S
ϕψ
)( yx
ψ
=
)( yx
ϕ
=
d
c
y
x
)(xgy
=
x
a b
y
)(xfy
=

27
Площадь фигуры,
ограниченной кри-
вой, заданной пара-
метрически
⎩
⎨
⎧
=
=
)(
)(
:
tyy
txx
AB
,
)(ty , )(tx , )(tx
′
– непрерывны,
)(tx
– монотонна при ];[
21
ttt
∈
,
)(
1
txa = , )(
2
txb
=
∫
′
=
2
1
t
t
dt)t(x)t(yS
Площадь сектора в
полярных координа-
тах
)( :
ϕ
rrAB = ,
)(
ϕ
r
– непрерывна при
];[
β
α
ϕ
∈
∫
=
β
α
ϕϕ
d)(rS
2
2
1
Длина дуги в декар-
товых координатах
)(xyy =
,
];[ bax
∈
,
)(xy , )(xy
′
–непрерывны на ]b;a[
∫
′
+=
b
a
dx))x(y(l
2
1
Длина дуги кривой,
заданной парамет-
рически
⎩
⎨
⎧
=
=
)(
)(
tyy
txx
,
];[
21
ttt
∈
)(tx
′
, )(ty
′
– непрерывны,
)(tx – монотонна при
];[
21
ttt
∈
∫
′
+
′
=
2
1
22
t
t
dt))t(y())t(x(l
Длина дуги кривой
в полярных коорди-
натах
)(rr
ϕ
= , ];[
β
α
ϕ
∈
, )(
ϕ
r , )(r
ϕ
′
–
непрерывны при
];[
β
α
ϕ
∈
∫
′
+=
β
α
ϕϕϕ
drrl
22
))(()(
Объем тел
∫
=
b
a
dxxSV )(
,
)x(S – площадь попе-
речного сечения
Объем тел вращения
Тело, полученное вращением
криволинейной трапеции
ABCD
вокруг оси
OX . f(x)yBC
=
: – не-
прерывна при
];[ bax
∈
∫
=
b
a
ox
dxxfV )(
2
π
α
β
B
x
O
A
A
B
a b
x
y
a
b
x
)(xS
x
y
A
B
C
D
y
x
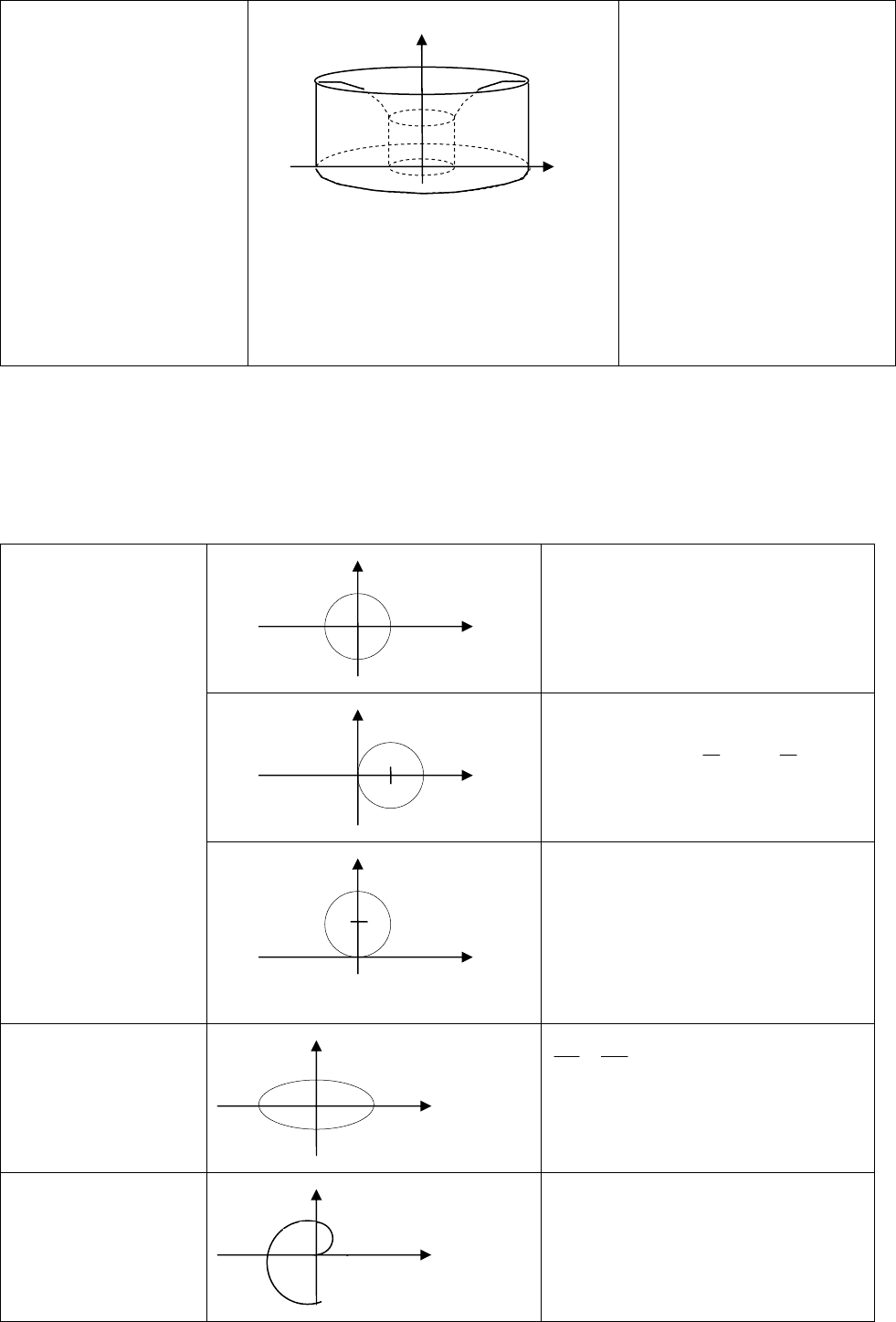
28
Тело, полученное вращением
криволинейной трапеции
ABCD
вокруг оси
OY .
f(x)yBC = : – непрерывна при
];[ bax ∈
∫
=
b
a
oy
dxxxfV )(2
π
5.10. Некоторые кривые, заданные параметрически или в полярных
координатах
Справочный материал, приведенный ниже, полезен для построения
кривых при решении задач темы «Приложения определенных интегралов».
222
ayx =+ ;
a
r
=
;
⎩
⎨
⎧
=
=
tsinay
,tcosax
(
π
20 <≤ t )
222
)( ayax =+− ;
ϕ
cosar 2
=
(
22
π
ϕ
π
≤≤− )
Окружность
222
)( aayx =−+ ;
ϕ
sinar 2
=
(
π
ϕ
≤≤0
)
Эллипс
1
2
2
2
2
=+
b
y
a
x
;
⎩
⎨
⎧
=
=
tsinby
,tcosax
(
π
20 <≤ t )
Спираль Архи-
меда
ϕ
a
r
=
(
);[ +∞∈ 0
ϕ
)
y
x
y
x
a
b
y
x
a
a
2
y
x
a
a2
y
x
a
A
B
C
D
x
y

29
Лемниската
Бернулли
ϕ
22 cosar = (
π
ϕ
20 <≤ )
n-лепестковая
роза
)3sin(
ϕ
ar =
)nsin(ar
ϕ
=
(или
)ncos(ar
ϕ
=
)
Астроида
⎪
⎩
⎪
⎨
⎧
=
=
tay
tax
3
3
sin
cos
, )2;0[
π
∈t
Циклоида
⎩
⎨
⎧
−=
−=
)cos1(
)sin(
tay
ttax
, );(
+
∞−∞∈t
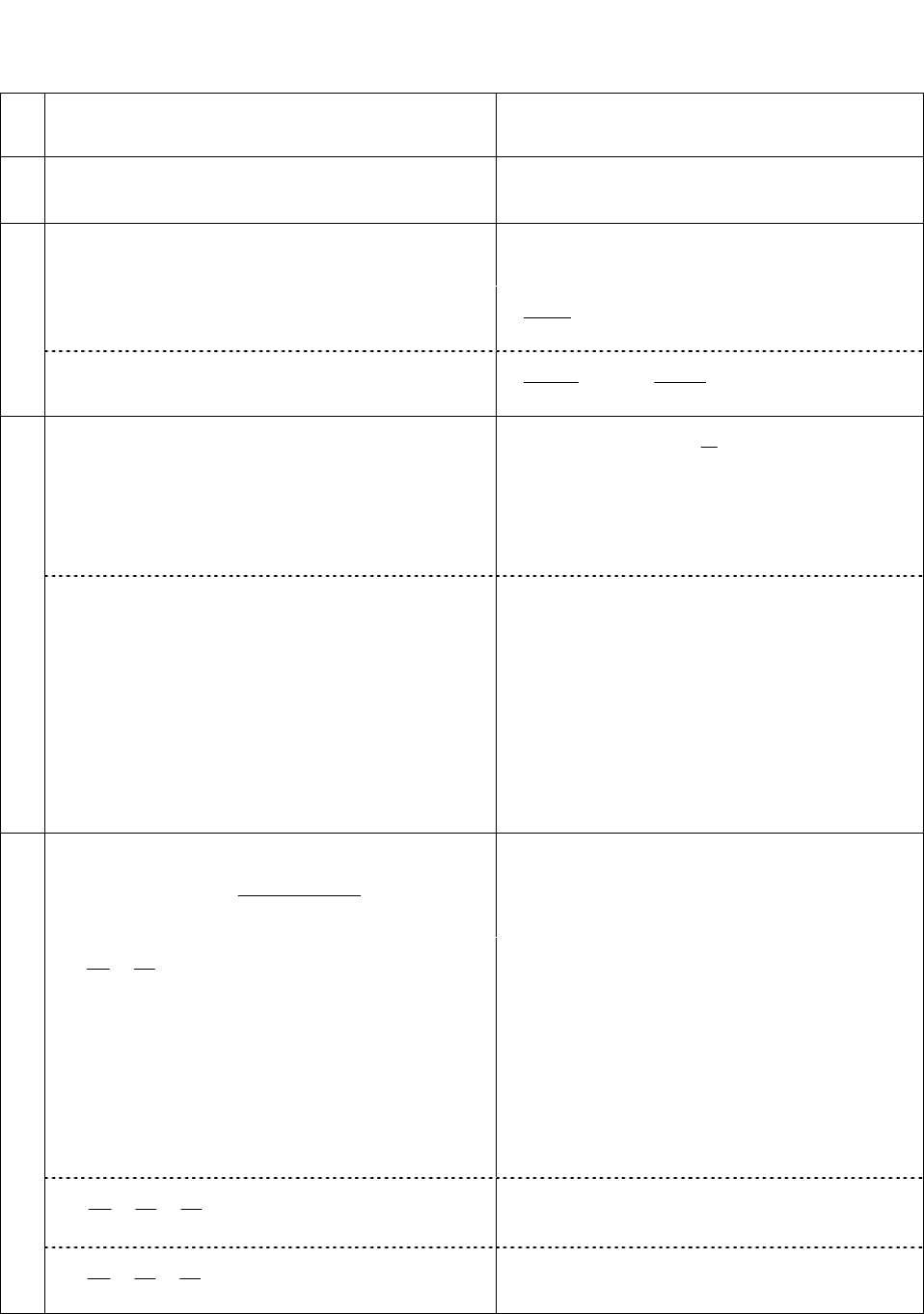
Кардиоида
)cos1(
ϕ
+
=
ar
)2;0[
π
ϕ
∈
)sin1(
ϕ
+
=
ar
)2;0[
π
ϕ
∈
a
a2
y
x
a
a2
x
y
a
a 2
π
x
y
x
y
x
0
a
a
x
y
30
6. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
6.1. Способы решения некоторых видов
дифференциальных уравнений I порядка
Вид уравнения Способ нахождения общего
решения
1. Уравнения с разделенными пере-
менными
dyyQdxxP )()( =
CdyyQdxxP +=
∫
∫
)()(
Уравнения с разделяющимися пере-
менными
a) )()( ygxfy ⋅=
′
,
Cdxxf
yg
dy
+=
∫∫
)(
)(
2.
б)
0
=
⋅+⋅ dy)y(Q)x(Pdx)y(N)x(M
Cdy
yN
yQ
dx
xP
xM
+−=
∫∫
)(
)(
)(
)(
а) Уравнение
);( yxfy =
′
является однородным,
если для любого
∈t R , 0 ≠t
)y;x(f)ty;tx(f = .
Подстановка
x
y
u =
,
откуда
x
uy
⋅
=
, uxuy +
′
=
′
,
приводит к уравнению с разде-
ляющимися переменными.
3.
б) Уравнение
0
=
+ dy)y;x(Qdx)y;x(P
является однородным уравнением,
если
);( yxP и );( yxQ функции одной
степени однородности, то есть
для любого
∈t R, 0 ≠t
)y;x(Pt)ty;tx(P
k
= , )y;x(Qt)ty;tx(Q
k
=
(
k – степень однородности).
Преобразовать уравнение к виду
3а, подстановка из п.3а.
Уравнения, сводимые к однородным
)(
111
cybxa
cbyax
fy
++
++
=
′
а)
11
b
b
a
a
≠
Замена
⎩
⎨
⎧
+=
+=
,y
,ux
β
α
v
где
α
,
β
найдены из системы
уравнений
⎩
⎨
⎧
=++
=++
.cba
,cba
0
0
111
βα
βα
б)
111
c
c
b
b
a
a
≠=
Замена
byaxz
+
=
.
4.
в)
111
c
c
b
b
a
a
==
Разделить переменные.
