Skiadas C.H., Dimotikalis I. (editors) Chaotic Systems: Theory and Applications
Подождите немного. Документ загружается.

288
K.
Qin
and
B.
1.
Dammen
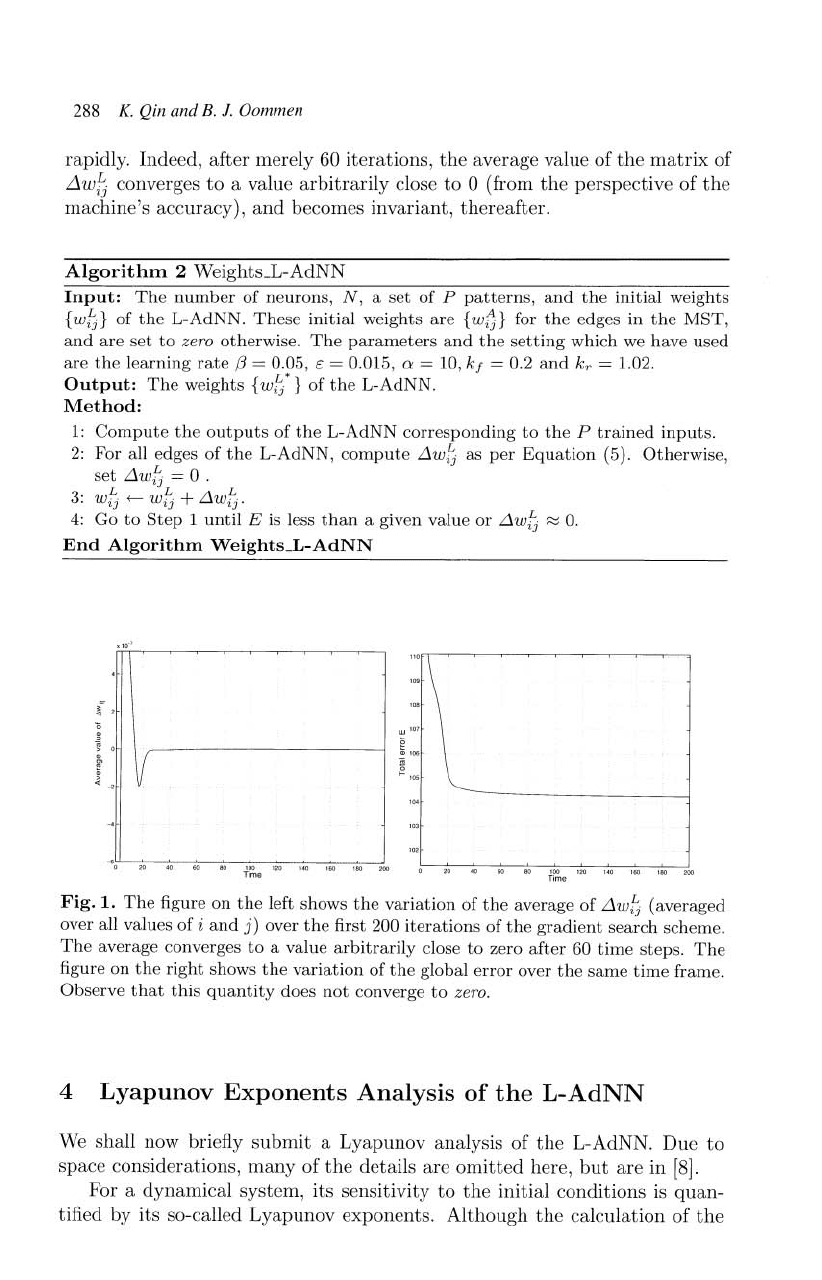
rapidly. Indeed,
after
merely
60
iterations,
the
average value of
the
matrix
of
L1wt
converges
to
a value
arbitrarily
close
to
0 (from
the
perspective
of
the
machine's
accuracy),
and
becomes
invariant,
thereafter.
Algorithm
2 Weights_L-AdNN
Input:
The
number
of
neurons,
N,
a
set
of
P
patterns,
and
the
initial
weights
{wt}
of
the
L-AdNN.
These
initial
weights
are
{wj}
for
the
edges
in
the
MST,
and
are
set
to
zero
otherwise.
The
parameters
and
the
setting
which
we
have
used
are
the
learning
rate
(3
= 0.05, c = 0.015,
Do
= 10, k
f
= 0.2
and
kr
= 1.02.
Output:
The
weights
{wt'}
of
the
L-AdNN.
Method:
1:
Compute
the
outputs
of
the
L-AdNN
corresponding
to
the
P
trained
inputs.
2:
For
all
edges
of
the
L-AdNN,
compute
L1w{j
as
per
Equation
(5).
Otherwise,
set
L1wt = 0 .
3:
wt
<-
wt
+ L1wt·
4:
Go
to
Step
1
until
E is less
than
a
given
value
or
L1wt
;:::;:
O.
End
Algorithm
Weights_L-AdNN
<10
'
f2
"
~
0
~
v
~
80
100 120 140 160
ISO
2'00
Time
W 107
C
rul06
"
"
1-'D5
SO
100 120 140
16.0
Time
Fig.
1.
The
figure
on
the
left
shows
the
variation
of
the
average
of
L1wt
(averaged
over all
values
of
i
and
j)
over
the
first 200
iterations
of
the
gradient
search
scheme.
The
average
converges
to
a
value
arbitrarily
close
to
zero
after
60
time
steps.
The
figure
on
the
right
shows
the
variation
of
the
global
error
over
the
same
time
frame.
Observe
that
this
quantity
does
not
converge
to
zero.
4
Lyapunov
Exponents
Analysis
of
the
L-
AdNN
We shall now briefly
submit
a
Lyapunov
analysis
of
the
L-AdNN.
Due
to
space
considerations,
many
of
the
details
are
omitted
here,
but
are
in
[8].
For a
dynamical
system,
its
sensitivity
to
the
initial
conditions
is
quan-
tified by
its
so-called
Lyapunov
exponents.
Although
the
calculation
of
the

Enhanced Tree-Shaped Adachi-Like Chaotic Neural Network 289
Lyapunov
expo
nents
by
directly
using a
Jacobian
analysis is
not
feasible.
However,
the
specific topology
and
state
update
equations
of
the
L-AdNN
makes
the
tas
k feasible,
as
we
shall
presently
see.
Considering
the
Jacobian
matrix
J
of
the
L-AdNN whose
structure,
topol-
ogy
and
weights
hav
e been
determined
in Section
3.
J
can
be seen
to
have
the
form:
J=(
[J~]
[J~
]
)
[J
ij
]
[J
ij
]
where each
[Ji~]
is
an
N x N
sub-matrix
of
J,
for 1
~
k
~
4, 1
~
i
~
Nand
1
~
j
~
N.
Each
[
Ji~]
is a res
ult
of
taking
the
parti
al derivatives
of
1]f(t +
1)
and
~f(
t +
1)
with
reg
ar
d
to
1]1
(t)
and
~1
(t)
resp
ect
ively as:
Ji~
(t)=
°b~b\~)l)
,
.1
j2
()
_
01J
f(t+l)
J3
()_O';f(t+l)
J 4
()
o.;f(t+l)
£.
.
ij
t -
o';f(t)
,
ij
t -
01Jf(t)'
ij
t
o';f(t)'
or
all 1
~
t
~
Nand
1
~
j
~
N;
By
taking
the
parti
al derivatives
after
considering
the
explicit forms
of
the
state
space
equations
given by
(1)
-
(3),
we
see
that
the
following closed
L*
form expressions for
Ji~(t)
result: (a):
JMt)
= k
f
+
~
.
xf(t)(l
-
xf(t))
L*
when
i =
j;
(b):
Ji~(t)
=
W~j
• •
Tf(t)(l
-
xf(t))
when
i #
j;
(c):
Ji~(t)
=
L*
~xf(t)(l
-
xf(t));
(d):
Ji~(t)
=
-%xf(
t)(l
-
xf(t))
when
i =
j;
(e):
J~(t)
= 0
when
i # j; (f):
Jt(t)
=
kr
-
%xf(t)(l
-
xf(
t))
when
i =
j;
(g):
Ji~(t)
= 0 when i #
j.
To get a
better
insight
of
the
dynamics, we observe, first of all,
the
term
xf(t)(l
-
xf(t))
has
an
asymptotic
value
of
zero for all i. Secondly, since
the
topology
of
the
L-AdNN
is tree-shaped,
wI;'
should
be
0 if
eij
is
not
in
T.
Further,
since
the
spanning
tree
topology does
not
contain
any
circles,
this
implies
wf;'
= 0 for all j = i.
Thus,
the
Jacobian
matrix
has
the
form:
kj
0
...
0 0 0
o 0
o
......
k
f
0
o 0
kr
0
o
o
o 0
o 0 0 . .
..
..
kr
Consequently, J(xo) =
J(xd
=
...
= J(Xk)'
The
Lyapunov
expon
en
ts
can
be
calculated
by
the
eigenvalues of
matrix
L(xo),
L(xo)
= lim
[J(k)
(J(k))TP
/2k
= lim [Jk(JT)k]1/
2k
= 1.
(6)
k---+
oo
k--HXJ

290
K.
Qin and
B.
1.
Oommen
Observe
that
this
matrix
has
2N
eigenvalues.
thus
the
Lyapunov
exponents
are: Al =
A2
=
...
= AN = log
kj,
AN+l = AN+2 =
...
=
A2N
= log k
r
.
By
choosing
the
values
of
the
coefficient as k
f
= 0.2,
kr
= 1.02, we
can
force
the
LLE
to
be
AN+l = AN+2 =
...
= A2N = log
1.02>
0,
rendering
the
L-AdNN
to
be
chaotic.
5
Chaotic
and
PR
Properties
of
the
AdNN
s
We
now briefly
report
the
comparative
PR
properties
of
the
L-AdNN
and
AdNN,
and
refer
the
reader
to
[8]
for
more
detailed
results.
These
properties
have
been
gleaned
as a
result
of
examining
the
Hamming
distance
between
the
input
pattern
and
the
patterns
that
appear
in
the
output.
5.1
Comparative
Chaotic
Properties
In
the
ideal
setting
we would
have
preferred
the
L-AdNN
to
be
chaotic
when
exposed
to
untrained
patterns,
and
the
output
to
appear
periodically
or
more
frequently
when
exposed
to
trained
patterns.
Besides yielding
this
phenomenon,
the
L-AdNN
also goes
through
a
chaotic
phase
and
a
PR
phase
as
some
of
its
parameters
change. We
summarize
the
results
for
the
L-AdNN
l
........
l~ l~
lr-l
l'"
l~~l~~l~~l~iL.i
l
~~
2 4 6
810
2 4 6
810
2 4 6
810
2 4 6
810
2 4 6
810
Fig.
2. The set of patterns used in Adachi et ai's and our experiments. The first
four
patterns
constitute
the
set used
by
Adachi et
al.
Pattern
5
is
an untrained
pattern, which represents
the
digit
5.
by
stating
that
by
using
different
settings
of
a
and
ai,
the
latter
demon-
strates
the
following
amazing
result
in
Figure
3.
From
this
Figure
we see
that
if
the
L-AdNN
is
presented
with
a trained
pattern,
the
output
is
the
same
trained
pattern
occurring
Frequently.
But
the
output
is
Chaotic
for
untrained
patterns.
While
this
phenomenon
is
not
observed
when
ai
= 2
(when
the
L-AdNN
is always
Chaotic),
the
Frequent
behaviour
is
noticeable
when
ai
= 2 +
6Xi.
Since a finer
measure
of
how closely
the
output
mimics
the
input
is
their
Hamming
distance
(which is
exactly
zero
if
the
output
is
an
precise
replica
of
the
input),
we
have
also
tabulated
the
frequency
of
the
Hamming
distance
within
the
first
1!
000
time
intervals
in
Table
1 for
the
various
input
patterns.
Table
1
demonstrates
that
this
distance
is close
to
zero (i.e.,
between
0
and
5)
quite
infrequently,
implying
that
under
these
settings,
the
L-AdNN
is
chaotic.
It
is
worth
mentioning
that
most
of
the
Hamming
distances
are
in

Enhanced Tree-Shaped Adachi-Like Chaotic Neural Network
291
(a)
(b)
Fig.
3.
The
Hamming
distance
between
the
output
and
the
trained
patterns
or
untrained
patterns
while
using
different
settings.
The
input
is
Pattern
4 in
both
(a)
and
(b).
The
external
stimulation
weights
are
ai
= 2
and
ai
= 2 +
6Xi
in
(a)
and
(b) respectively.
The
output
graph
are
displayed
for
pattern
1,
pattern
4
and
pattern
5.
Table
1.
The
frequency
distribution
of
the
Hamming
distance
between
the
input
and
the
output
as
the
measure
occurs
within
10 intervals,
when
the
external
input
is
ai
=
2,
and
the
refractory
factor
ct
= 10.
HamIlling
distance
Input
Pattern
[0,5J
116,19J
[20,29J
[30,39J [40,49J [50,59J [60,69J [70,79J
1180,89J
[90,100J
Pattern
1 1
3
25 129 279
397 143 22 1
0
Pattern
2
3 5 33 121 291 374 146 24 3
0
Pattern
3 1 2 15
117 342 358 146 18 1
0
Pattern
4 1
6
12
157 338 339 121 24 2
0
the
interval
[40,59] - i.e.,
almost
50%
erroneous
pattern,
which is
what
we
expect
from a
truly
noisy
pattern.
If
the
same
settings
are
used
in
the
AdNN,
the
system
behaves
as
an
AM, which
has
been
well
illustrated
by
Adachi
and
his
co-authors
in
their
paper
[1].
5.2
Comparative
PR
Properties
If
the
parameters
of
the
AdNN
are
set
as
prescribed
in
[1],
and
the
AdNN
weights
the
external
inputs
with
ai
= 2 +
6Xi,
the
system
becomes closer
to
mimicing a
PR
phenomenon.
Adachi
et
al
claim
that
such
a
NN
yields
the
stored
pattern
at
the
output
periodically
with
a
small
periodicity. However,
it
turns
out
that
if
the
input
is
an
untrained
pattern,
the
AdNN
can
still retrieve
it
and
the other
four
trained patterns
with
relatively lower frequency.
This
property
is
more
or
less
one
which resembles
an
AM
system
instead
of
a
PR
system.
This
can
be
seen from
Table
2.
As
opposed
to
this, for
the
L-AdNN,
the
most
interesting
scenario occurs
when
C\'
= 10
and
the
weight for
the
external
input
is
ai
= 2 +
6Xi'
In
this
case,
the
system's
output
is
noticeably
chaotic.
But
the
input
pattern
can
be
retrieved
very frequently as long
as
the
input
is
one
of
the
trained
patterns.

292
K.
Qin
and
B.
1.
Oommen
Table
2.
The
AdNN:
In
this
table,
the
input
is
the
untrained
Pattern
5
in
Figure
2.
The
numbers
in
this
table
are
the
frequencies
of
each
pattern
being
retrieved
within
the
first
1,
000
time
intervals.
We
clarify
this
by
explaining
Figure
3 (b)
in
greater
detail.
The
input
is
Pattern
4,
the
output
displays
the
input
(Pattern
4)
or
a
reasonably
similar
pattern
with
a
very
high
frequency
- as
demonstrated
by
the
low
Hamming
distance.
The
Hamming
distance
between
the
output
and
all
the
other
pat-
terns
-
the
trained
and
the
untrained
pattern
- is
noticeably
very
large
(i.e.,
with
almost
50% noise).
The
corresponding
table
of
Hamming
distances
is given
in
Table
3. Con-
sider
the
first
column
of
Table
3.
The
reader
will
observe
that
the
trained
input
patterns
can
be
approximately
retrieved
almost
20%
of
the
time.
On
the
contrary,
when
encountering
an
untrained
input
pattern
(Pattern
5 in
Figure
2), it is
observed
in
the
output
with
a
much
lower frequency - less
than
5%.
Adachi
and
his
co-authors
did
observe
this
for
the
AdNN,
namely
that
the
system
with
the
external
stimulations
yielded a
stored
pattern
with
a
relative
higher
frequency,
and
an
untrained
pattern
with
relative
lower fre-
quency
-
which
phenomenon
can
be
utilized
to
achieve
PR.
The
amazing
point
here
is
that
the
L-AdNN
displays
the
same
phenomenon
even
though
it
merely
has
a
linear-
number
of
connections,
and
the
fact
that
the
weights
used
are
not
directly
obtained
from
the
patterns
themselves,
but
by
migrating
from
the
latter
by
using
a
gradient
search
algorithm.
As far as we know,
anal-
ogous
properties
have
not
been
reported
earlier
for
any
type
of
NN
(chaotic
or
otherwise).
The
unabridged
paper
[8]
also
presents
a
comparative
analysis
of
the
quasi-energy
function
properties
of
the
L-AdNN
and
the
AdNN,
omitted
here
due
to
space
considerations.
Table
3.
The
frequency
distribution
of
the
Hamming
distance
between
the
input
and
the
output
as
the
measure
occurs
within
10
intervals,
when
the
external
input
is
0i
= 2 +
6x;
and
the
refractory
factor
ex
= 10.
Hamming
distance
Input
Pattern
[0,5]
[6,19]
[20,29]
[30,39] [40,49] [50,59] [60,69] [70,79]
[80,89]
[90,100]
Pattern
1
217
342
226
112
63
28
10
2
0 0
Pattern
2
197
369
222
131
58
21 1
J 0 0
Pattern
3
198
325
251
130
57
32
3 4
0 0
Pattern
4
196
357
235
126
54
25
5
2
0 0
Pattern
5
46
495
334
104
18
2
0 1 0 0
6
Conclusions
In
this
paper
we
have
concentrated
on
the
field
of
Chaotic
Pattern
Recog-
nition
(PR),
which is a relatively
new
sub-field
of
PR.
Such
systems,
which
have
only
recently
been
investigated,
demonstrate
chaotic
behavior
under

Enhanced Tree-Shaped Adachi-Like Chaotic Neural Network 293
normal
conditions,
and
resonate
when
it
is
presented
with
a
pattern
that
it
is
trained
with.
The
network
which we
have
investigated
is
the
Adachi
Neural
Network
(AdNN)
[1-5],
which
has
been
shown
to
possess
chaotic
properties,
and
to
also
demonstrate
Associative
Memory
(AM)
and
Pattern
Recognition
(PR)
characteristics.
Because
its
structure
involves a
completely
connected
graph,
the
computational
complexity
of
the
AdNN
is
quadratic
in
the
num-
ber
of
neurons.
In
this
paper
we
have
considered
how
the
computations
can
be
significantly
reduced
by
merely
using
a
linear
number
of
computations.
To achieve this, we
have
extracted
from
the
original
completely
connected
graph,
one
of
its
spanning
trees
and
then
computed
the
best
weights for
this
spanning
tree
by
using
a
gradient-based
algorithm.
Apart
from a Lya-
punov
analysis
and
an
analysis
of
the
quasi-energy
function
found
in
[8],
by
a
detailed
experimental
suite,
we show
that
the
new
linear-time
AdNN-like
network
possesses
chaotic
and
PR
properties
for different
settings.
References
1.M.
Adachi
and
K.
Aihara.
Associative
dynamics
in
a
chaotic
neural
network.
Neural Networks,
10(1):83-98,
1997.
2.M.
Adachi
and
K.
Aihara.
Characteristics
of
associative
chaotic
neural
networks
with
weighted
pattern
storage-a
pattern
is
stored
stronger
than
others.
In
The 6th
International
Conference
on
Neural
Information
Processing, Perth,
Australia,
volume
3,
pages
1028-1032,
1999.
3.M.
Adachi,
K.
Aihara,
and
M.
Kotani.
Pattern
dynamics
of
chaotic
neural
net-
works
with
nearest-neighbor
couplings.
In
Circuits
and
Systems,
1991,
IEEE
International
Sympoisum
on,
Westin
Stanford
and
Westin
Plaza. Singapore,
volume
2,
pages
1180-1183,
June
1991.
4.M.
Adachi,
K.
Aihara,
and
M.
Kotani.
An
analysis
of
associative
dynamics
in
a
chaotic
neural
network
with
external
stimulation.
In
Proceedings
of
1993
International
Joint
Conference
on
Neural Networks, Nagoya, Japan,
volume
1,
pages
409-412,
1993.
5.K.
Aihara,
T.
Takabe,
and
M.
Toyoda.
Chaotic
neural
networks.
Physics Letters
A, 144:333-340, 1990.
6.D.
Calitoiu,
B.J.
Gommen,
and
D.
Nussbaum.
Desynchronzing
of
chaotic
pattern
recognition
neural
network
to
model
inaccurate
parception.
IEEE
Transaction
on
Systems, Man, and Cybernetics-part B:Cybernetics,
37(3):692-704,
2007.
7.D.
Calitoiu,
B.J.
Gommen,
and
D.
Nussbaum.
Periodicity
and
stability
issues
of
a
chaotic
pattern
recognition
Neural
Network.
Pattern
Anal
Applic,
pages
175-188,
2007.
8.Qin
Ke
and
B.
J.
Gommen.
Adachi-like
chaotic
neural
networks
requiring
linear-
time
computations
by
enforcing
a
tree-shaped
topology.
In
Unabridged Version
of
This paper, 2008.
9.Qin
Ke
and
B.
J.
Gommen.
Chaotic
pattern
recognition:
The
spectrum
of
prop-
erties
of
the
adachi
neural
network.
In
The 12th
International
Workshop
on
Structural and
Synaptic
Pattern
Recognition and 7th
International
Workshop
on Statistical
Pattern
Recognition,
December
2008.

294
Clustering
of
Inertial
Particles
In
3D
Steady
Flows
Themistoklis Sapsis
1
and
George Haller
2
1
Massachusetts
Institute
of
Technology
Department
of
Mechanical
Engineering
Cambridge,
MA
02139,
USA
(e-mail:
sapsis@mit.
edu)
2
Massachusetts
Institute
of
Technology
Department
of
Mechanical
Engineering
Cambridge,
MA
02139,
USA
(e-mail:
ghaller@mit.edu)
Abstract:
We
study
the
motion
of
inertial
particles
in
three-dimensional
steady
fluid flows
that
contain
a family
of
two-dimensional
invariant
manifolds.
Using
results
from
Ergodic
Theory
we
derive
a
condition
that
predicts
if
the
considered
invariant
manifold
for
the
flow will
persist
as
an
invariant
manifold
for
inertial
par-
ticles.
We
illustrate
our
results
for
the
three-dimensional
ABC
flow
with
paremeters
corresponding
to
a
non-integrable
case.
Keywords:
inertial
particles,
Ergodic
Theory,
Melnikov
Theory.
1
Introduction
-
Setup
The
motion
of small particles in fluid flows is a
common
phenomenon
encoun-
tered
both
in
nature
(e.g.
contaminant
dispersion
in
the
atmosphere)
as well
as in
many
technological applications (e.g. chemical
systems
involving
partic-
ulate
reactant
mixing).
In
dilute
flows
with
particles
having
different density
from
the
fluid, a
particularly
interesting
behavior
that
has
been
observed
both
numerically
and
experimentally
is
particle
clustering.
This
refers
to
the
tendency
of
particles
to
concentrate
in
narrow
bands
and
is
due
to
the
fact
that
the
equations
of
motion
for
inertial
particles
are
considerably different
from
those
for fluid parcels,
as
inertial
and
viscous effects
playa
significant
role.
Several works have
analyzed
inertial
particle
dynamics
in
either
analyti-
cally defined or numerically
generated
fluid flows (cf. Haller
and
Sapsis
[6]'
Burns
et
al.
[3],
Yannacopoulos
et
al.
[11],
Rubin
et
al.
[9],
Maxey
and
Riley [8]).
In
this
work
we
study
clustering
properties
of small spherical
par-
ticles in three-dimensional
steady
flows
that
contain
a single
or
a family
of
closed
invariant
manifolds.
In
particular,
we
derive a necessary
condition
for
the
persistence of
an
invariant
manifold
that
has
no
stagnation
points
as
an
attractor
for
inertial
particles.
Let
u (x)
represents
the
velocity field a three-dimensional
steady
fluid flow
of
density P
f.
The
fluid fills
the
compact
spatial
region D
with
boundary
aD;

Clustering
of
Inertial Particles in
3D
Steady Flows 295
we assume
that
V is a uniformly
bounded
smooth
manifold for all times. We
also assume
that
u (x) is a
smooth
function for all
of
its
arguments
. We
denote
the
material
derivative
of
the
velocity field by
Du
Dt
= (\7u)
u,
(1)
where
\7
denotes
the
gradient
operator
with
respect
to
the
spatial
variable
x. We also assume
that
u (x) is volume preserving, i.e.
\7.
u =
o.
For a particle p of
den
sity
Pp
immersed
in
the
fluid we denote
with
x (t) its
path.
Let
the
particle
be
spherical
with
radius
a « L,
with
L deno
ting
a
characteristic
length
scale in
the
flow, Re
the
Reynolds number,
and
v (t) =
x (t)
the
Lagrangian
velocity
of
the
spherical
particl
e.
In
this case
the
particle
satisfies
the
Maxey-Riley eq
uation
of
motion
(cf., e
.g
. Maxey
and
Riley
[8],
Benczik et
al.
[2
] or
Babiano
et
at.
[1])
where
1
E = - « 1,
fJ
x= v
.
3R
Du
(x, t)
EV=
U (x, t) - V
+E
- ,
2
Dt
R
fJ
=
St'
2
(a)2
St
= 9 L
Re.
(2a)
(2b)
Note
that
the
larger
the
in
ert
ia
param
ete
r
fJ,
th
e less significant
the
effect
of
inertia; in
the
fJ
-->
00
limit, (2b) describes
th
e
motion
of
a passive ideal
tracer
particle.
The
density
ratio
R distinguishes
neutrally
buoyant
particles
(R = 2
/3)
from aerosols
(0
< R < 2
/3)
a
nd
bubbl
es
(2/3
< R < 2). In
what
follows we will consider only non-n
eutra
lly
buoyant
particles.
Using geo
metric
singular
perturb
ation
theory
Haller
and
Sapsis
[6]
proved
that
for E > 0 small enough,
equation
(2b)
admits
a globally
attracting
invariant slow manifold
that
has
the
form
{
(
3R
)
Du(x
,t) 2 }
ME
= (x, V
s
) : Vs = u (x, t) + E 2 - 1
Dt
+
O(E)
.
(3)
By
reducing
the
dynamics
on
the
slow manifold ME
it
is shown
that
particle
motion
is governed by
the
inertial
eq
'uation
(
3R
)
Du(x,t)
2
x=u(X,t)+E
2 -
1
Dt
+O(E).
(4)

296
T.
Sapsis and C. Haller
2
Attracting
invariant
manifolds
for
inertial
particles
For two-dimensional, steady, flows
the
motion
of
inertial
particles
is governed
by
the
autonomous,
two-dimensional
ODE
(4) from which powerful conclu-
sions
about
the
asymptotic
nature
of
finite-size
particles
can
be
concluded
(cf.
Rubin
et
al.
[9],
Haller
and
Sapsis
[6]).
In
what
follows we provide a
general
result
for
three-dimensional,
volume
preserving
flows
having
a family
of
invariant
manifolds
concerning
the
persistence
of
these
slow manifolds
as
attractors
for
inertial
particles.
Theorem
1.
Let
u (x)
be
a three-dimensional, autonomous, volume-
preserving, vector field and
So
a compact, two-dimensional, invariant mani-
fold, with
unitary
normal vector
fi.
(x) on which the
motion
is non-resonant.
Mor-eover,
we
assume that
Ilu
(x)11
> 0 for all x ESo. Then a necessary con-
dition for the persistence
of
So
as
an invariant manifold for inertial particles
is
e
R
-1)
iT
Du
I (So)
==
lim 2
Ilu
(ip
(t, xo))ll
fi.
(ip
(t, xo)) -
(ip
(t, xo)) dt = 0
T--+CXJ
T 0
Dt
(5)
where xoESo.
In
this case the flow on
So
is ergodic with probability density
function
for
the position
of
an inertial par-ticle on
So
given by
f(x)
=
Iso
Ilu(Y)II-1d!r(y)'
x ESo.
(6)
Proof.
Let
SE
be
a
compact,
two-dimensional,
invariant
manifold
with
a well
defined
interior
for
the
steady
inertial
equation
(4). We
assume
that
SE
varies
smoothly
for f
:::0:
O.
The
phase
space
volume
bounded
by
SE
does
not
change
in
time,
therefore
r \7.
[u
(x) + f
(3R
_
1)
Du
(x)
+
0(f
2
)]
dV
(x)
Jlnt(S,)
2
Dt
= f
(3R
_
1)
r \7.
[DU
(x) +
O(f)]
dV
(x)
2
Jlnt(S,)
Dt
Dividing by f
and
taking
the
f
---+
0 limit, we
obtain
that
1
Du
(x)
\7·--dV
(x) = 0
Int(So)
Dt
must
hold for
the
compact
streamsurface
So
of u (x).
By
applying
the
diver-
gence
theorem
on
Int(So)
we
obtain
1
Du
(x) 1
Du
(x)
~
\7·--dV
(x) =
--n
(x)da
(x) = 0
Int(So)
Dt
So
Dt

Clustering
of
Inertial Particles in
3D
Steady Flows 297
where
dO"
(x) is
the
infini
tesima
l
area
element
(Riemannian
volume)
of
So
at
x.
Let
us now consider
the
flow
of
the
dyn
amical
system
on
the
two dimensional
torus
So.
As we
hav
e
assumed
the
motion
on
So
is non-resonant. In this case,
as
it
is proven by Kolmogorov
[7]
(see also Sinai
[10D,
there
exists
an
infinitely
differentiable change of coordinates where
the
system
reduces
to
dii
dt = 1,
diJ
-=a
dt
(ii,
iJ)
E
S2
(7)
where a is such
that
the
pair
(1,
a)
are
Diophantine
frequencies or equivalently
a
is
norm
ally
approximated
by
rational
numbers
(cf.
Sinai
[10]).
Hence,
any
trajectory
of
(7) will fill
out
densely
the
torus
S2
preserving
the
Lebesgue
measure
on
it.
Thus,
the
flow
on
So
will
be
ergodic
and
by Liouville
Theorem
(see e.g. Sinai
[10])
the
invariant measure will
be
given by
J.L
(x) = Ilu
(x)II-
1
dO"
(x) x E
So.
Hence,
we
can
apply
the
Birkhoff-Khinchin Ergodic
Theorem
to
obtain
r
DUD(X)
ii
(x)dO'
(x) =
lim
-T
1
r lIu
(<p
(t, xo)) II
ii
(<p
(t, xo))
DD
u
(<p
(t, xo)) dt=O
iso
t
T~oo
io
t
for every
Xo
E
So.
Moreover, by considering
the
Radon-Nikodym
derivative
of
the
invariant
measur
e
J.L
(x)
we
obtain
the
probability density function for
a finite-size
particle
on
So,
i.e.
the
concentration
of
in
ert
ial particles on
So
f
(x)
=
J~o
Ilu (y)
11
-
1
dO'
(y) ,
x
ESo
.
This
completes
the
proof
of
the
theorem.
To
estimate
the
quantity
I (So) from a finite
time
interval we exploit
the
Central
Limit
Theorem
for
dynamical
systems (cf.
Burton
and
Denker
[4]).
More specifically by
setting
eR-1)j,T
Du
IT
(So,xo) = 2 T a Il
u(
'P(t, xo))IIfi.(
<p(
t,xo))
Dt
('P(t,xo))dt
(8)
there
exists a positive
number
~
such
th
at
for every
(3
E
lR.
j
1
1(3
(X2)
f(x)dO" (x)
~
~
exp
-2
dx
u
T
v
27r
-<Xl
{l
where
Ul
=
{x
ESo
:
~T
[IT
(So,
x)
-
I(So)]
< (3}. Thus,
the
rate
of
con-
vergence
of
IT
(So,
x)
to
I (So) is
of
order
0
(T
-
1)
.
The
stability
of a streamsurface
So
for which I (So) = 0
can
be
verified
by checking
whether
the
phase
space volume grown
or
shrinks
on
either
side
of
So.
For a
sta
ble
SE
we
must
have
(9)
