Skiadas C.H., Dimotikalis I. (editors) Chaotic Systems: Theory and Applications
Подождите немного. Документ загружается.

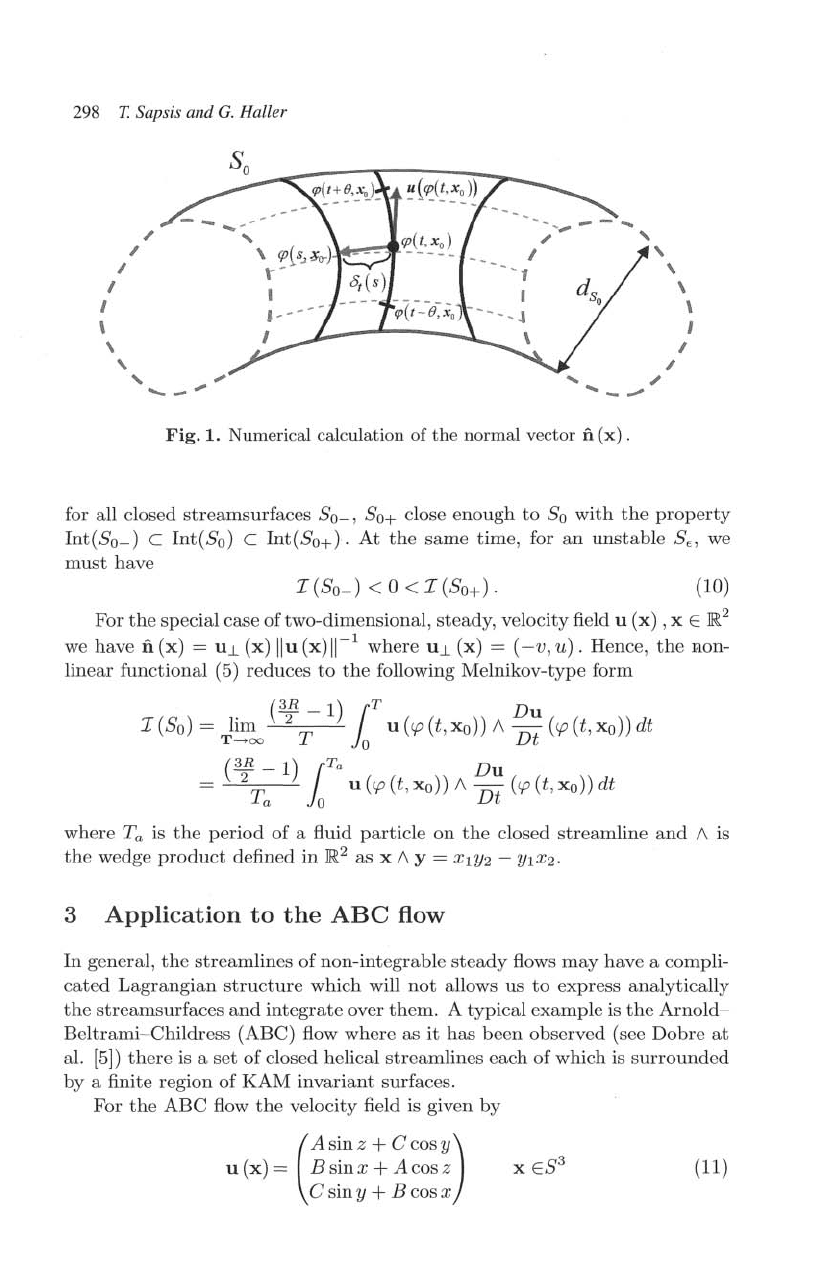
298 T Sapsis and G. Haller
I
I
\
'\
I
"
'\.
.......
-
"",'"
Fig.
1.
Numerical
calculation
of
the
normal
vector
fi
(x)
.
\
\
\
I
I
/
for all closed streamsurfaces
50~
,
5
0
+ close enough
to
50
with
the
property
Int(50~)
C
Int(5
0
)
C
Int(5
0
+
}.
At
the
same
time
, for
an
unstable
5
e
,
we
must
have
(10)
For
the
special case
oftwo
-dimcusional,
ste
ady, velocity field u (x) ,x E
]R2
we have flex) =
U..L
(x)
lI
u(x)
l
l~l
where U
..L
(x) = (- v,
u).
Hence,
the
non-
linear functional
(5)
reduces
to
the
following Melnikov-type form
e
R
-
1)
r
T
Du
I
(So)
=
}~~
2 T
.fa
u(cp(t,xo)) A
Dt
(cp(t,xo))dt
=
(¥T~
1)
laT
a U(cp(t,
XO))
A
~~
(cp
(t,XO)) dt
where
Ta
is
the
period of a fluid particle on
the
closed
st
reamline
and
A is
the
wedge
product
defined in
]R2
as x A y = :rl1/2 -
:t)lX2.
3
Application
to
the
ABC
flow
In
general,
the
streamlines of non-integrable
steady
flows
may
have a compli-
cate
d
Lagran
g
ian
structur
e which will
not
allows us
to
express analytically
the
streamsurfaces
and
integrate
over
them.
A typical example is
th
e Arnold-
Beltrami
- Childress (ABC)
flow
where as
it
has been observed (see Dobre
at
al.
[5])
there
is a set of closed helical streamlines each of which is surrounded
by
a finite region of
KAM
invariant surfaces.
For
the
ABC flow
the
velocity field is given
by
(
ASin Z
+
CCOS
Y)
u (x) =
Bsinx
+
Acos
z
C sin y + B cos x
(11)
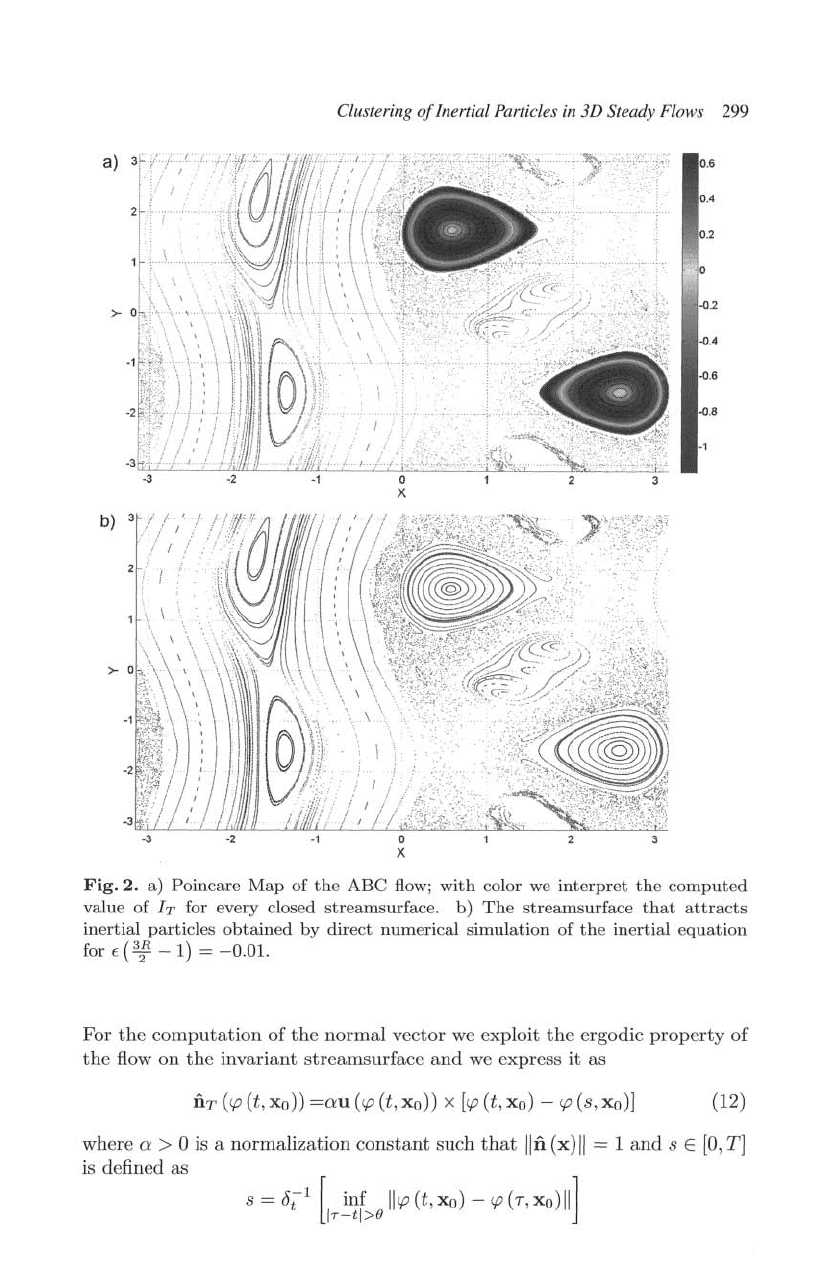
Clustering
of
Inertial Particles in 3D Steady Flows 299
a)
>-
x
Fig.
2.
a)
Poincare
Map
of
the
ABC
flow;
with
col
or
we
interpret
the
comp
uted
value
of
IT for every closed
streams
urfac
e.
b)
The
streamsurface
that
attracts
in
ertia
l
particles
obtained
by direct
numerical
simu
lation
of
the
inerti
al
equation
for
t(
3:
-
1)
=
-0.01.
For
the
computation
of
the
normal vector
we
exploit
the
ergodic
property
of
the
flow
on
the
invariant streamsurface
and
we express
it
as
nT(ip(i,xo))
=O:
U(ip(t,xo)) x
[rp
(t,x
o)
- ip(s,xo)]
(12
)
where
0:
> a
is
a normalization
constant
such
that
lin
(x)11
= 1
and
8 E
[0,
T]
is defined as
8=0;-1
[ inf Ilip(t,XO)-ip(T,
Xo)ll]
I.,.-tl>f)
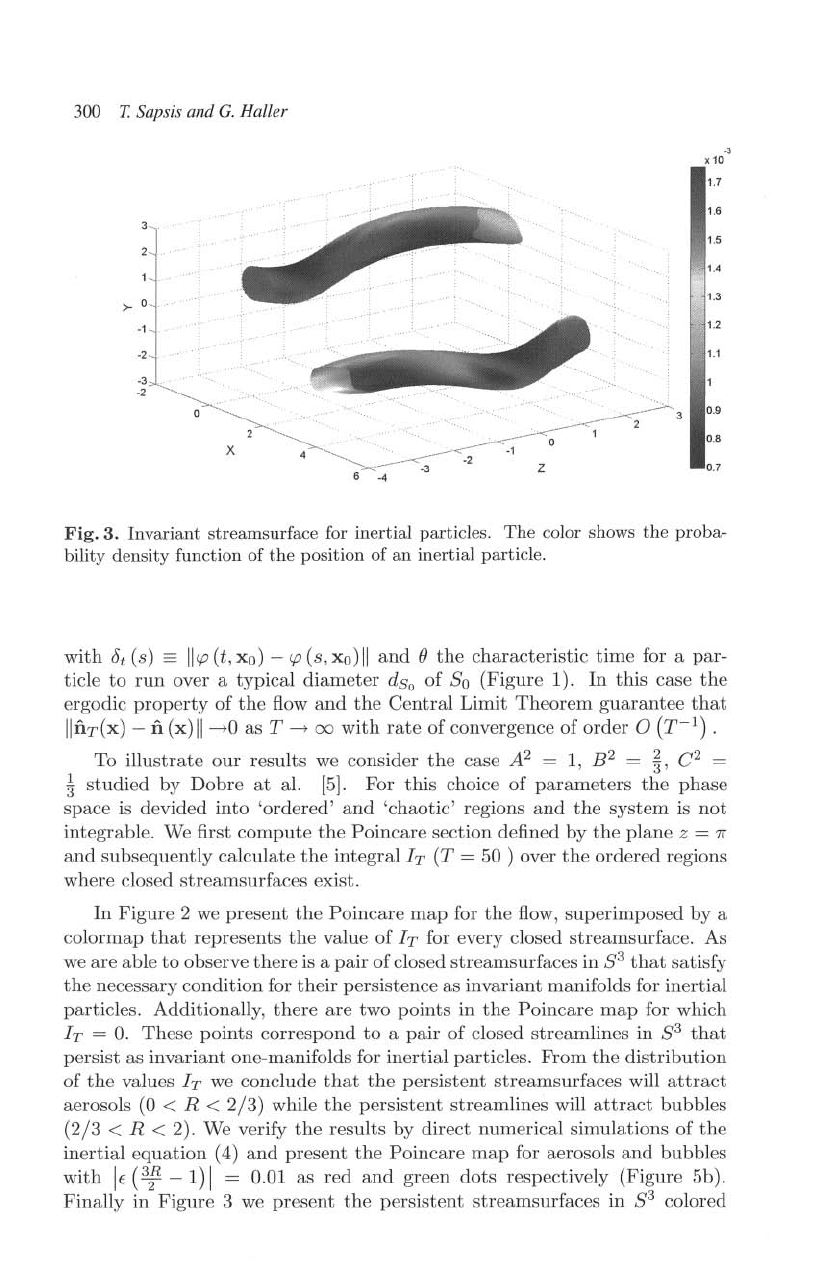
300
T.
Sapsis and
U.
Haller
x
-2
-3
-4
-,
,.
x 10"
I
::
'1.5
~~
f;~~11A
I::
1
:~1'1
'1
'0.9
0,8
0,(
Fig.
3.
Invariant
streamsllrface for
inertial
particles.
The
color
shO\vs
the
proba-,
bility
density
function
of
the
position
of
an
inertial
particle.
with
Ot
(s)
==
11'P(t,xo) - 'P(s,xo)11
and
()
the
characteristic
time
for a
par-
ticle
to
run
over a typical
diameter
ds
o
of
8
0
(Figure 1). In
this
ease
the
ergodic
property
of
the
flow
and
the
Central
Limit
Theorem
gua.rantee
that
IlnT'(x)
-
11
(x)
II~'O
as
T-.,
00
with
rate
of
convergence
of
order
0
(r-l)
.
To
illustrate
our
results
we
consider
the
ease A
2
1, 8
2
=
~)
C
2
=
~
studied
by
Dobre
at
aL
[5].
For this choice
of
parameters
the
phase
space is devided
into
'ordered'
and
'chaotic' regions
and
the
system
is
not
integrable.
vVe
first
compute
the
Poincare
section defined by
the
plane z =
1\
and
sub"equently calculate
the
integral IT' (1' =
50
) over
the
ordered regions
where closed streamsurfaces
exist.
In
Figure 2
we
present
the
F)oincare
map
for
the
flow, superimposed by a
colornlap
that
represents
the
value
of
h· for every closed streamsurface. As
we
are
able
to
observe
there
is a
pair
of
dosed
streamsurfaces
in
S<l
that
satisl:v
the necessary condition for
their
persistence as invariant manifolds for inertial
particles. AdditionaHy.
there
are
two
points
in
the
Poincare
map
for which
IT
O.
These
points
correspond
to
a
pair
of
dosed
streamlines
in
8
3
that
persist as invariant one-manifolds for inertial particles,
From
the
distribution
of
the
valuesTy·
we
conclude
that
the
persistent streamsurfaees will
attract
aerosols
(0
< R < 2/;3) while
the
persistent
streamlines ,\fill
attract
bubbles
(2/;5
< R < 2).
vVe
verify
the
results by direct numerical simulations of
the
inertia.l
equation
(4)
and
present
the
Poincare
map
for aerosols
and
bubbles
with
IE
e2R-l)1
=
(Un
as red
and
green dots respectively (Figure 5b).
Finally in
Figure
:3
we
present
the
persistent
streamsurfaces
in
8
3
colored

Clustering
of
Inertial Particles in
3D
Steady Flows
301
according
to
the
probability
density
function
calculated
through
equation
(6).
4
Conclusions
We have
studied
clustering
properties
of
inertial
particles
in
three-dimensional,
steady
flow fields. Using results
of
Ergodic
theory
we have derived a nec-
essary condition for
the
persistence
of
any
closed
invariant
manifold as a
two-dimensional
invariant
manifold for
inertial
particles.
This
condition
has
the
form
of
a nonlinear functional
that
acts
on
the
unitary
normal
bundle
of
the
streamsurface
and
any
non-resonant
trajectory
that
lies
on
it. We have
illustrated
our
theoretical
findings
through
a
non-integrable
case,
the
ABC
flow,
and
we have
determined
clustering regions for
non-neutrally
buoyant
particles.
Acknowledgements
This
research was
supported
by
NSF
Grant
DMS-04-04845,
AFOSR
Grant
AFOSR
FA 9550-06-0092,
and
an
MIT
Presidential
Fellowship.
References
1.A.
Babiano,
J.
H. E.
Cartwright,
O.
Piro,
and
A.
Provenzale.
Dynamics
of
a
small
neutrally
buoyant
sphere
in a fluid
and
targeting
in
hamiltonian
systems.
Phys.
Rev. Lett., 84:5764, 2000.
2.1.
J.
Benczik,
Z.
Toroczkai,
and
T.
Tel. Selective
sensitivity
of
open
chaotic
flows
on
inertial
tracer
advection:
Catching
particles
with
a stick. Phys. Rev. Lett.,
89:164501,
2002.
3.T.
Burns,
R. Davis,
and
E. Moore. A
perturbation
study
of
particle
dynamics
in
a
plane
wake
flow.
J.
Fluid
Mech., 384:1, 1999.
4.R.
Burton
and
M.
Denker.
On
the
central
limit
theorem
for
dynamical
systems.
Trans.
Amer.
Math. Soc., 302:715, 1987.
5.T.
Dombre,
U. Frisch,
J.
M.
Greene,
M.
Hinon,
A.
Mehr,
and
A. M. Soward.
Chaotic
streamlines
in
the
abc
flows.
J.
Fluid
Mech., 167:353, 1986.
6.G.
Haller
and
T.
Sapsis.
Where
do
inertial
particles
go
in
fluid flows?
Physica
D, 237:573, 2008.
7.A. N. Kolmogorov.
On
dynamical
systems
with
an
integral
invariant
on
the
torus.
Dokl.
Akad.
Nauk, 93:763, 1953.
8.M.
Maxey
and
J.
Riley.
Equation
of
motion
for a
small
rigid
sphere
in a
nonuni-
form
flow. Phys. Fluids, 26:883, 1983.
9.J.
Rubin,
C.
K.
R.
T.
Jones,
and
M. Maxey.
Settling
and
asymptotic
motion
of
aerosol
particles
in a cellular flow field.
J.
Nonlinear
Sci., 5:337, 1995.
W.YA.
G. Sinai.
Introduction
to
ergodic
theory.
Princeton
University Press, 1976.
11.A. N.
Yannacopoulos,
G.
Rowlands,
and
G. P. King.
Influence
of
particle
inertia
and
basset
force
on
tracer
dynamics:
Analytic
results
in
the
small-inertia
limit.
Phys. Rev. E, 55:4148, 1997.

302
A Two Population Model for the
Stock Market Problem
Christos
H.
Skiadas
Technical University
of
Crete, Chania, Crete, Greece
(e-mail:
skiadas@asmda.net)
Abstract: The development
of
the last year disaster in the Stock Markets all over the
world gave rise to reconsidering the previous models used. It is clear that, even in an
organized international or national context, large fluctuations and sudden losses may
occur. This paper explores a two populations' model. The populations are conflicting into
the same environment (a Stock Market) by following the main rules present, that
is
mutual interaction between adopters, potential adopters, word-of-mouth communication
and
of
course by taking into consideration the innovation diffusion process. The
proposed model has special futures expressed by third order terms providing
characteristic stationary points.
Keywords: chaotic modeling, the stock market problem, stock market, innovation
diffusion modeling, Lotka-Volterra, simulation, chaotic simulation.
1.
Introduction
Several attempts to model the stock-market problem can be found in the
literature. Between these models the Lotka-Volterra modeling approach is
of
considerable interest. The model can be used
if
we
assume two interacting
populations and can be generalized to more than two. The case
of
two
interacting populations
is
explored by using two coupled differential equations
and the results found give rise to a limit cycle and the corresponding oscillating
graphs over time, Skiadas,
2009 [7]. However, the Lotka-Volterra system
of
differential equations, a non-linear system
of
the second order, fails to explain
the sudden growth and decline resulting into the stock-market environment and
even more the stability to high or low values (capital gains or losses).
In
view
of
the last year losses in the stock markets globally
it
would be very important to
reconsider the classical Lotka-Volterra theory by introducing into the
corresponding equations terms having to do with the diffusion aspect
of
the
communication process. The proposed model has special futures expressed
by
third order terms providing characteristic stationary points.
It
should be noted
that a seminal paper was published by Harold Hotteling
[1]
during March 1929
few months before the big crash in the New York stock exchange. Hotelling, in
this paper explored the "stability
in
competition" problem. The analysis
proposed was based in a simplification
of
the problem. Only two markets where
competing; however, the results where extremely important and clarified the
situation.
In
this paper
we
accept the same methodology supposing that there is
a stock market with two interacting populations and we explore the arising case.
That is new is the introduction
of
the theories
of
the last decades on the

A
Two
Populatiol1 Model
for
the Stock Market Problem 303
adoption-diffusion
of
innovations in developing the equations
of
the proposed
model.
2. The Model and Simulations
To model the specific situation
we
take into account that two populations x and
yare
present into the stock market and interact each other. Even more to
simplify the case we suppose that the variables
XI
and y, stand for the number
of
players or for the number
of
transactions or for the values
of
the stocks
belonging to each part
of
the players at a specific time period
t.
The aim is to
explore the behavior
of
the two populations during time and especially in the
limits.
A model including the main characteristics
of
two interrelating or even
conflicting popUlations into a stock market can be expressed by the following
set
of
differential equations:
i = a
j
Y + a
2
xy
+ a
3
x(l-
y)
+ a
4
yx(k
-
x)
y
=b
j
x+b
2
xy+b
3
y(k
-x)+b
4
xy(l-
y),
where aj,
a2,
a3,
a4
and bj,
bz,
b
3
,
b
4
are parameters expressing the mutual
interaction
of
the populations X and y. The parameters k and I express the upper
limit
of
the popUlations x and y respectively.
The first term to the right stands for the flows from the one part to the other
whereas the second term expresses the mutual interaction between the active
parts
of
the populations x and
y.
If
we
retain the first two terms to the right the
proposed model is
of
the Lotka-Volterra type.
The non active parts
of
the populations are
(k
-
x)
for x and (l - y) for the
population
y. The interaction
of
these parts with the active popUlations y and x is
expressed with the third terms to the right
of
the above differential equations
(see
[2,
3,4,
5,
6]).
The fourth terms to the right include the terms
x(k
-
x)
and
y(l
-
y)
multiplied by
y and x respectively. These terms account to the rates
of
adoption-diffusion that
is
extremely important in order to express the word-of-mouth communication
between adopters (the active part
of
the players) and potential adopters (the non-
active part
of
the players).
Looking back to the set
of
the two differential equations above we see that
we
have two third degree equations for x and
y.
In the following we check the
influence
of
the third order term to the stock-market model. To this end the
above model is simplified to the following form:
• 2
X =
-ay
+ cyx
. b
2
Y =
x-cxy
,

304
C.
H.
Skiadas
Where
a,
band
c are parameters
of
interaction. Especially the parameter c is
selected to be the same
in
both equations expressing the coupling
of
both
populations
x and y.
The set
of
the last equations takes the form:
i =
-ay
+ cyx
2
=
-cyra;;(.Ja/
c -
x)-
c.xy(Ja/ c - x)
y = bx -
cxy2
=
cx~(.Jb/
c - y)+
c.xy(~
-
y),
The last equations include in the right part side two basic parts
of
the interaction
and the diffusion process where
x = ra;; and y = .J b / c are the upper limit
or the maximum for
x and y respectively.
There
is
a fixed point at (0,
0)
and four other characteristic points at
(x
= ra;; , y = .J b /
c),
(x
= ra;; , y =
-~
)
(x=-ra;;
,y
=~),
(x=-ra;;
,y
=-~)
The last differential equations give the following differential equation for x and
y:
dy
bx-cxy2
dx
-ax+cyx
2
The solution
is
(l-b/c)(X2
-a/c)=h
Where h
is
the integration constant.
The next Figure illustrates characteristic graphs
of
the last equation. The four
characteristic points define a rectangle. Into this space are drawn few
of
the
trajectories
of
the process. The trajectories outside
of
the rectangle diverge
to
infinity.

A
Two
Population Model
for
the Stock Market Problem 305
)
---~.
-
~
--
----
Figure
1.
Characteristic Trajectories for various
h.
As
it is presented in Figure 1 there appear to be positive and negative values for
the stock-market process. To be realistic
we
will move the main part, that is the
rectangle space, inside the first quarter (the positive space)
of
the Cartesian
Coordinates. This
is
achieved by introducing the transformation x*=x-el and
y*=y-
e
2·
The resulting set
of
differential equations is:
x =
-a(y
- e
2
)
+
c(y
- e
2
)(x
- e
j
)2
y =
b(x
- e
j
) -
c(x
- e
j
)(Y - e
2
)2
,
Where x stands for x* and y for y*.
We can also find the corresponding difference equation form for this system by
observing that
.
dx
Lix
x
t
+
1
-
x
t
X = -
""
- = =
Xt+1
-
xr
dt
M
(t
+
1)
- t
. dy
i1y
Yr+l
- Y
r
Y
=
dt
""
---;; =
(t
+
1)
- t =
Yt+j
- Y
r
The resulting difference equations set
is:
X
t
+
1
=xr
-a(Yr
-e
2
)+C(Yr
-e
2
)(x
r
_e
j
)2
Yr+l
= Y
r
+b(xr
-el)-c(x
r
-ej)(Yr
-e
2
)2,
An illustration
of
this difference equations' model appear
in
Figure
2.
There is
an unstable fixed point located at
(e"
e2) and the four fixed points at the corners

306
C.
H.
Skiadas
of
the rectangle. The process can stabilized at any
of
the four points depending
on the starting values
or
on values
of
the parameters. That is extremely
important is that we may have four specific cases when
aJter some time the
process
is stabilized in which:
I.
(x
= e
1
-+;;;t;. y:::: e
2
-+
-Jb/
c);
both gains
2. (x:::: e
J
+
-Ja/
c,)'::::; e
2
-
-Jb/
c
);x
gains,y losses
3. ( X ::: e
J
--
J;;iz,
. y = e
2
+,J
b / c
);
x losses, y gains
4.
(x
= e
j
-,J a / c
,y
::-..:
e
2
-.J
b / c
);
both losses
In Figure
2 the third case appears by means that y gains and x losses. The upper
part
of
the figure illustrates the charactelistic rectangle whereas the time varying
development
of
x and y is presented. The original sinusoidal oscillations give
rise to step
like oscillations and finally to a stable process where x retain losses
and y keep their gains. The process has stopped at the upper left hand side
of
the
charactclistic rectangle indicated
by a small circle (see fjgure 2). The starting
point was inside the characteristic
rectangle and the movement was counter-
clockwise.
-~-----
V U
(-.J
'-------------
Figure 2. The Difference Equations model (Case 3)
For
a simpler presentation
of
the findings
we
use the previous difference
equation without the linear movement expressed
by ej and
ez
by
setting
el=O
and
ez=O.
The resulting form is
J
x
r
+]
:::::
XI
-
aY
t
-+
eytx
t
-
2
Yt+l
==)'/
+bX
t
-ext)'t
'
The Jacobian
of
this map
is

A
7\1'0
Population Modelfor the Stock
Marker
Problem 307
] +2cxy
l(x,),)
= 1
b-cy~
The value
of
the Jacobian at the characteristic point (0, 0) is:
J (0,0)
=:
1 + ab . Assuming positive parameters a and h the point (0,0) is
unstable.
The Jacobian
at the other 4 characteristic points
(±,j
a / c
,±,jb
/
c)
is
J (0,0)
=:
1-
4ab, and for appropriate positive values
of
the parameters the 4
points are stable (attracting).
The resulting graphs are presented in the following four figures (Fig.3-Fig.6)
where the four different cases
of
gains and losses appear for various statiing
values
of
Xo and
Yo.
The parameters selected are a=0.06,
h=O.03
and c=0.025. A
small circle in the appropriate comer
of
the charactetistic rectangle indicates the
stopping case. In Figure 3 this circle
is at the upper light hand comer, in Figure
4
is at the lower right part
of
the rectangle whereas, in Figure 5 the circle is at
the upper left part and in Figure 6 the
circle is located at the lower left hand
side.
In
the latter case both x and y is stabilized at the lower values
of
the
process with losses.
lih
frt,
(T--===
¥@Tl1tj-------
tt~fJt\-m:\-t==
1].1
l::t'
L':t------
Fig. 3
(xo=O.5,
Yo=O)
Fig. 4
(xo=O.55,
Yo=O)
5
(xo=O.6,
Yo=O)
Fig. 6
(xo==O.65,
Yo=O)
Model Simulations
