Смольников А.П. Теория автоматического управления
Подождите немного. Документ загружается.


143
где b(p) и c(p) – характеристические полиномы соответственного контура
регулирования, определенного матрицей
А-ВК и контура оценки состояния,
определенного матрицей
A-LC
b(p)= det[pI - (A - BK)],
c(p)= det[pI - (A - LC)].
Таким образом, динамика замкнутой системы в целом определяется
динамическим поведением контура регулирования и контура оценки
состояния. Однако их динамика может быть
выбрана независимо и не влияет
друг на друга. Если оба полинома устойчивы, то их произведение – также
устойчивый полином.
МОДУЛЬ 2. ДИСКРЕТНЫЕ СИСТЕМЫ АВТОМАТИЧЕКОГО
УПРАВЛЕНИЯ
РАЗДЕЛ 3. ЛИНЕЙНЫЕ ИМПУЛЬСНЫЕ СИСТЕМЫ
16. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ИМПУЛЬСНЫХ СИСТЕМ
16.1. Определение линейных импульсных систем
Импульсными системами автоматического регулирования называются
системы, содержащие
импульсное звено, то есть звено, преобразующее
непрерывное входное воздействие
()
x
t в последовательность
импульсов
()
и
x
t .
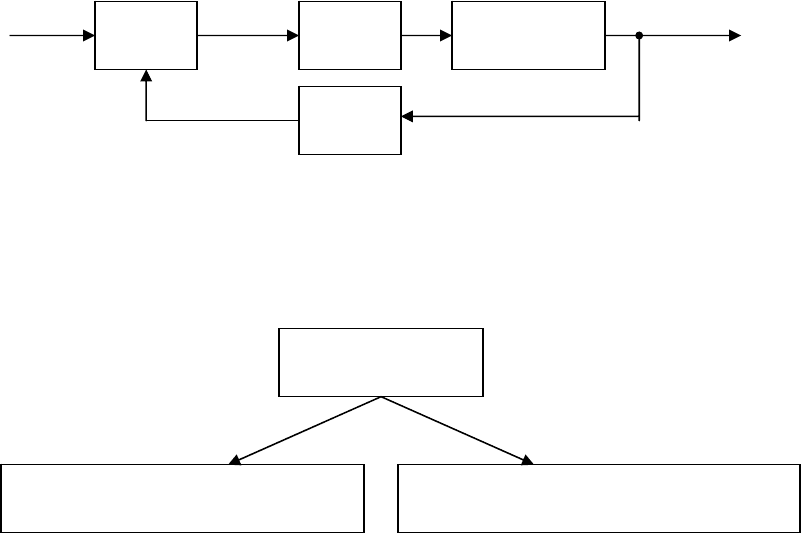
Рис. 16.1. Импульсная система
ИЗ
Управляем
-
u(t) x x
и
y
144
Различают также цифровые системы. В цифровой системе сигналы в
одной или нескольких точках представляются цифровыми кодами, с
которыми оперирует ЭВМ.
Рис. 16.2. Цифровая система
Дискретные системы объединяют все системы, в которых сигналы
имеют цифровую или импульсную форму.
Рис. 16.3
Области применения импульсных систем широки и в основном эти
системы могут быть разделены на две группы:
1) Системы, где информация существует лишь в моменты съема (или
измерения):
• радиолокационные системы;
• системы передачи данных, обслуживающие одновременно несколько
систем управления;
• системы управления с цифровыми вычислительными устройствами.
2) Системы, в которых информация намеренно вводится только в
дискретные моменты времени, хотя она существует непрерывно.
То есть квантование вводится специально в следующих случаях:
• когда систему с квантованием можно сделать более точной за
счет отсутствия нагрузки между моментами съема данных;
• когда система управления позволяет поочередно решать
несколько задач управления;
• при управлении процессами, где благодаря квантованию
достигается более экономичное использование приборов, измеряющих
температуру, давление, расход.
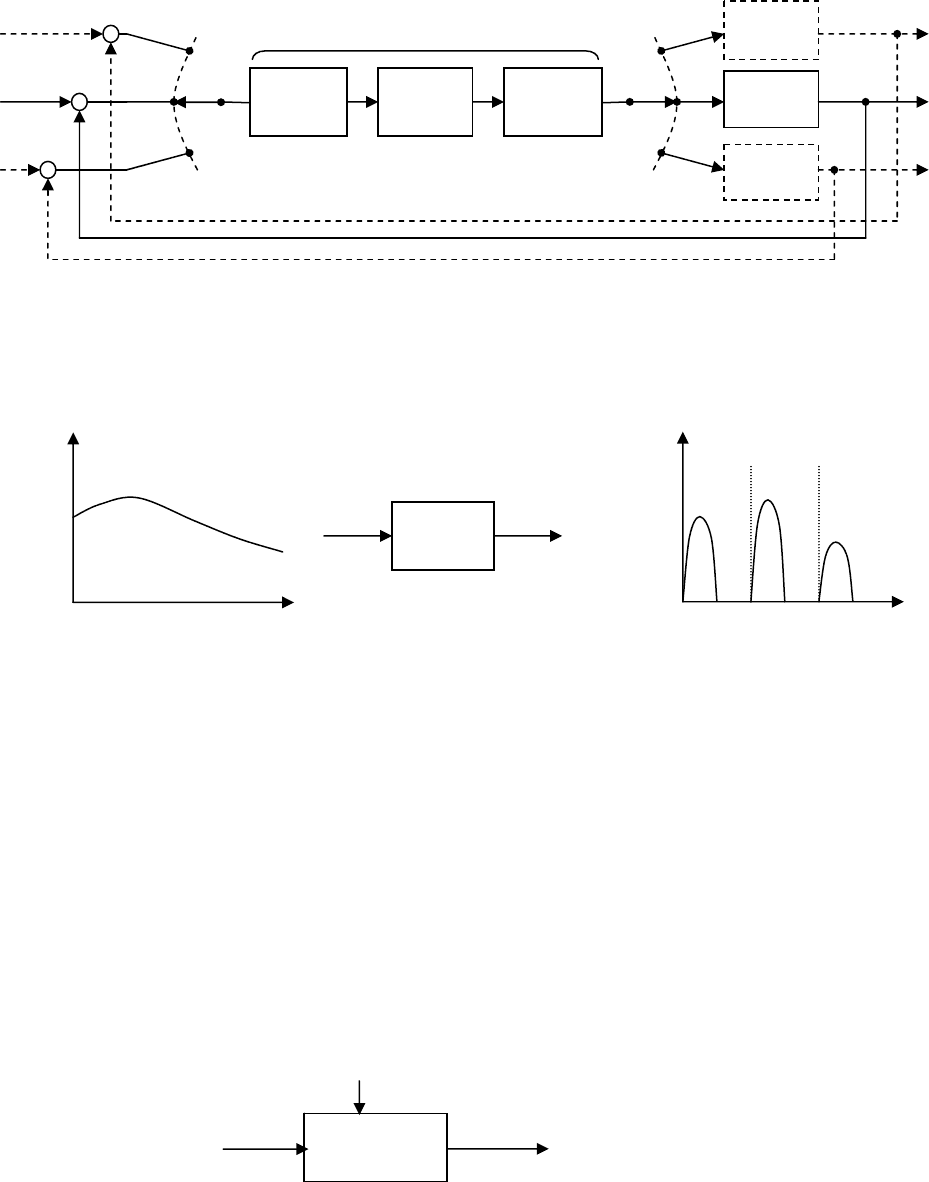
Дискретные
системы
Импульсные
(
квантование по в
р
емени
)
Цифровые
(
квантование по
ур
овню и в
р
емени
)
ЦАП
Управляем
Цифровой.
код
y
АЦП
ЭВМ
145
Особенно большое развитие получили ИС в последние годы, когда в
САУ начали использовать цифровые вычислительные машины и цифровые
устройства.
Рис. 16.4. Пример импульсной системы с ЦВМ
Подобная структура (рис. 16.4) часто встречается в системах АСУ ТП.
Импульсное звено может быть представлено в виде
Рис. 16. 5
ИЗ представляет собой преобразователь или импульсный модулятор,
который преобразует входную функцию ()
x
t в последовательность
импульсов, промодулированных по амплитуде, длительности или частоте.
16.2. Виды модуляции сигналов
16.2.1. Общее понятие амплитудной модуляции сигналов
Амплитудной модуляции соответствует схема
Рис. 16.6
Выходной модулированный амплитудный сигнал
()
и
x
t определяется
выражением:
ЦАП
y
1
АЦП
ЦВМ
Регулятор
Объект
1
Объект
2
Объект
3
y
2
y
3
x
,3
x
1
x
2
-
-
-
Коммутатор Коммутатор
x(t)
t
И
x(t)
x
и
(t)
x
и
(t)
t
0
T
2
АИ
модулятор
()
x
t
()ft
()
и
xt
146
x
и
(t) =
∑
∞
=
−
0
)()(
l
lTtflTx ,
где
() ()
tlT
xlT xt
=
=
– решетчатая функция l = 0,1,2,3,…
T – период квантования ,
ω
0
= 2
π
/T – частота квантования,
f(t) – модулирующая функция
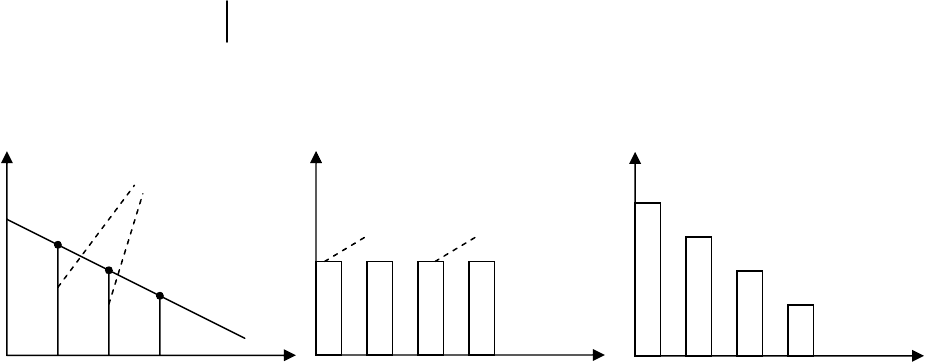
а б в
Рис. 16.7
В общем случае
f(t) =
⎪
⎩
⎪
⎨
⎧
≤≤≠
случаяхдругихв
Ttпри
0
00
в данном случае f(t) =
⎪
⎩
⎪
⎨
⎧
≤≤
≤≤
TtTпри
Ttпри
2/0
2/01
.
Импульсная амплитудная модуляция – это линейная операция.
Если x
1
(t)
→
x
1,И
(t) и x
2
(t)
→
x
2,И
(t), то
с
1
x
1
(t)+ с
2
x
2
(t)
→
с
1
x
1,И
(t)+ с
2
x
2,И
(t).
В качестве модулирующей функции часто используется дельта-
функция, то есть:
f(t)=
δ
(t), тогда x
*
(t) =
∑
∞
=
−
0
)()(
l
lTtlTx
δ
.
Рассмотрим некоторые виды импульсных звеньев.
16.2.2. ИЗ с амплитудной и широтной модуляцией
В САУ наиболее часто встречаются звенья с амплитудной модуляцией.
()
x
t
t
x(0) x(T) x(2T)
x(3T)
T 2T 3T
x(lT)
t
T 2T 3T
f(t)
1
f(t-2T)
∑
∞
=
−
0
)(
l
lTtf
t
T 2T 3T
x
и
(t)
147
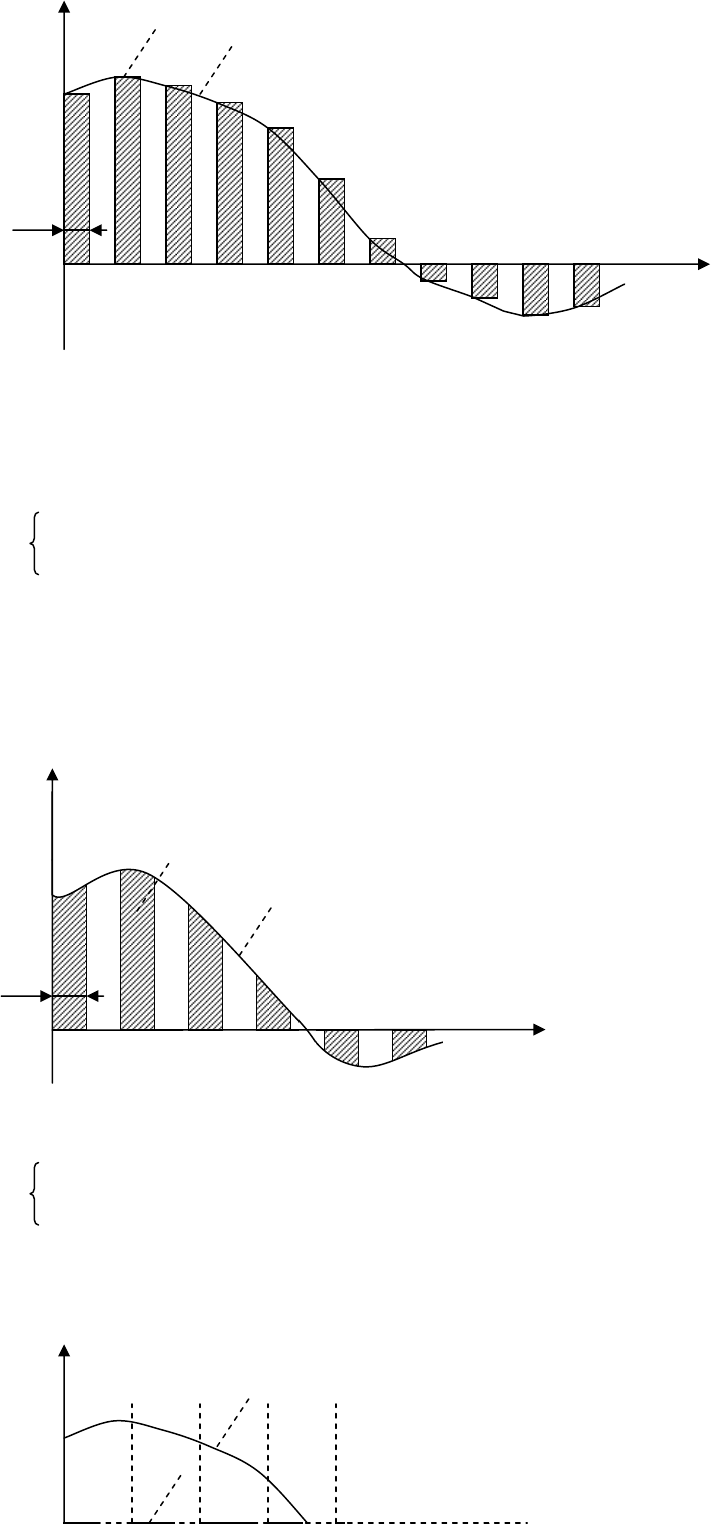
1. ИЗ с амплитудной модуляцией первого рода.
Рис. 16.8
()
и
x
t – представляет собой последовательность прямоугольных
импульсов
длительностью γT, при γ ≤ 1
x
И
= kx(lT) при lT
≤
t
≤
(lT +
γ
T)
x
И
= 0 при (lT +
γ
T)
<
t
<
(l + 1)T
l = 0,1,2,3,…;
γ
= const.
2. ИЗ с амплитудной модуляцией второго рода.
Рис. 16.9
x
И
= kx(t) при lT
≤
t
≤
(lT +
γ
T)
x
И
= 0 при (lT +
γ
T)
<
t
<
(l + 1)T
l = 0,1,2,3,…;
γ
= const.
3
. ИЗ с широтно-импульсной модуляцией (ШИМ).
x
t
T 2T 3T
4T 5T
γT
x
x
И
x
x
x
И
x
t
T 2T 3T 4T 5T
x
x
И
γ
T
148
Рис. 16.10
Звено с ШИМ описывается следующими уравнениями:
x
И
=С sign x[lT] при lT
≤
t
≤
(lT +
γ
T)
x
И
= 0 при (lT +
γ
T)
<
t
<
(l + 1)T
γ
= k /x[lT]/; l = 0,1,2,3,…; С= const.
Если длительность импульсов невелика по сравнению с
длительностью переходных процессов в системе, то системы с широтной
модуляцией импульсов приближаются по своим свойствам к системам с
амплитудной модуляцией и могут быть описаны линейными уравнениями.
16.3. Эквивалентная схема импульсной системы
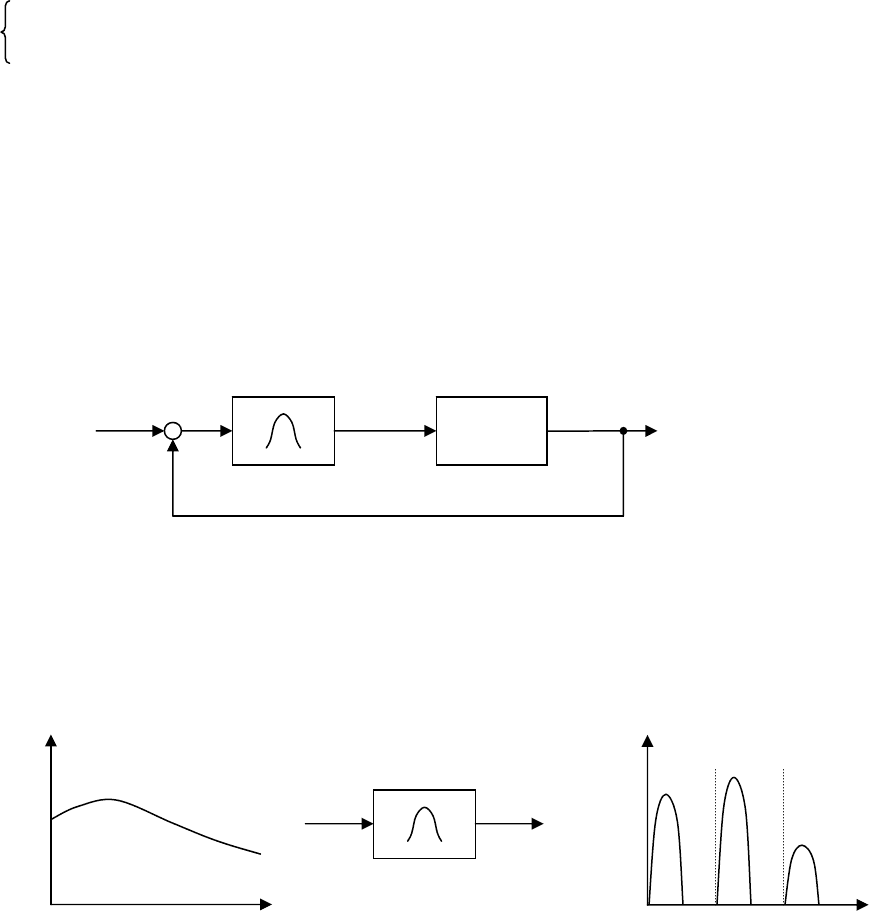
Структурная схема импульсной САУ имеет вид (рис. 16.11).
Рис. 16.11
Система содержит ИЗ и непрерывную часть с передаточной функцией
W
Н
(p). На вход ИЗ подается непрерывная величина, на выходе получаем
последовательность импульсов.
W
Н
(p)
x
вх
-
x x
И
НЧ
x
вых
x(t)
t
x
и
(t)
t
0 T 2T
x(t) x
и
(t)
ИЗ
149
Рис. 16.12
Форма импульсов произвольна и зависит от конкретной реализации
звена. Она характеризуется функцией f(t), равной нулю вне интервала
0
<
t
≤
T.
Рис. 16.13
Для периода 0
≤
t
<
∞
импульсный сигнал
x
и
(t) =
∑
∞
=
−
0
)()(
l
lTtflTx
.
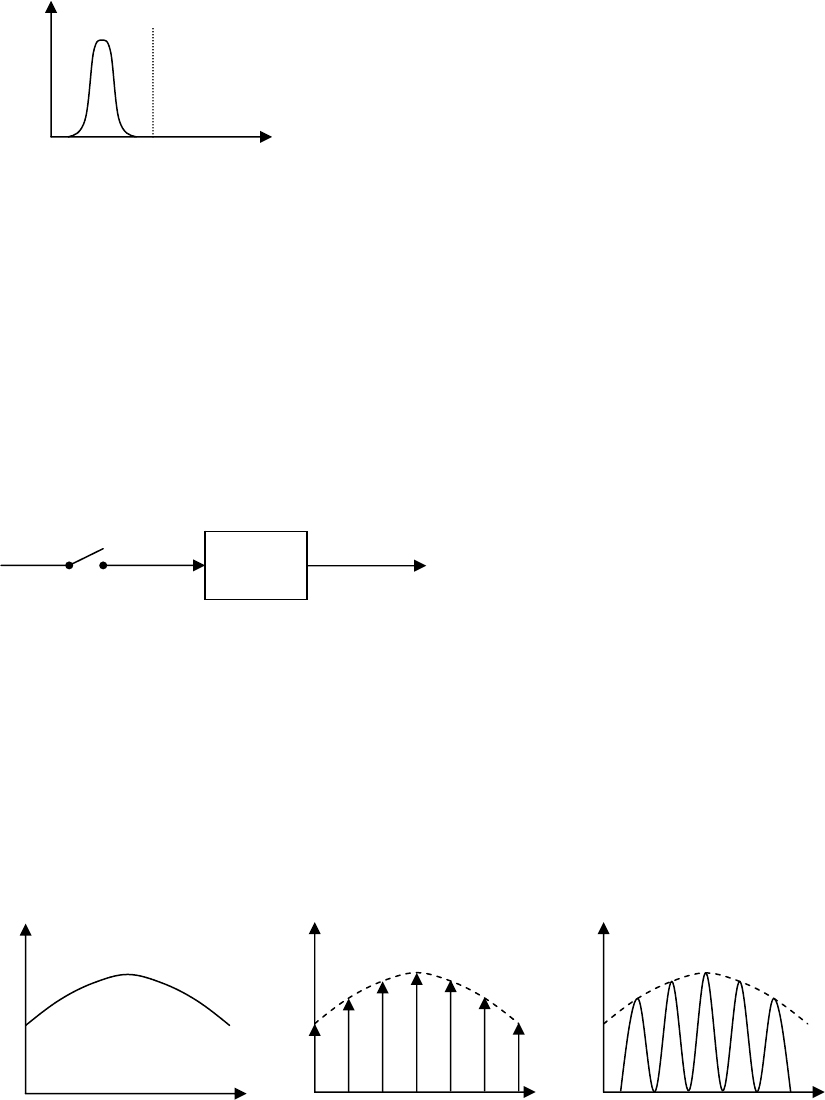
Для расчета заменим реальное ИЗ – идеальным (простейшим)
импульсным звеном (ИИЗ) и формирующим звеном (ФЗ), которые
соединяются последовательно (рис. 16.14).
Рис. 16.14
Сигналы в схеме на рис.16.14 имеют вид (рис. 16.15).
ИИЗ преобразует x(t) в x
*
(t), который представляет собой
последовательность мгновенных импульсов с амплитудой равной
∞ и
периодом Т, причем площадь каждого импульса равна значению x(t) в
момент lT.
а б в
Рис. 16.15
f(t)
t
0
T
W
ф
(p)
x(
t
)
x
*
(
t
)
x
И
(
t
)
ИИЗ
ФЗ
x(t)
t
x
*
(t)
t
x
И
(t)
t
T 2T 3T 4T

150
При t = lT следует x
*
(lT) = x(lT)*
δ
(0), то есть амплитуда→∞, поэтому
изображение x
*
(t) условное и импульсы (рис. 16.15,б) изображаются разной
длины условно пропорциональной их площади.
Допустим, что при t
<
0 , x(t) = 0. Тогда последовательность
импульсов x
*
(t) может быть записана:
x
*
(t) =
∑
∞
=
−
0
)()(
l
lTtlTx
δ
,
где x(lT) – значение входного сигнала в момент времени lT,
δ
(t) –
дельта-функция со свойствами:
() 1()tt
δ
′
=
);
∫
∞
∞−
dtt)(
δ
=1; функция
δ
(t) равна
нулю везде, кроме точки t = 0.
На входе формирующего звена в момент времени t = lT действует
импульс x
*
(t), площадь которого равна x(lT)
×
1.
Формирующее звено должно иметь реакцию на единичный импульс
(то есть весовую функцию), тождественную форме действующих в системе
импульсов
() ()
ф
wt ft
=
Для этого передаточная функция ФЗ должна быть равна
изображению функции f(t), так как изображением единичного импульса
является единица, то есть
() ()
ф
Wp Fp
=
.
Таким образом, передаточная функция ФЗ W
ф
(p) зависит от формы
импульса на выходе реального ИЗ и определяется по выражению:
W
ф
(p)=
∫∫
∞
−
∞
−
=
00
)()( dtetfdtetw
ptpt
ф
.
Для распространенного случая, когда формируются импульсы
прямоугольной формы (длительности
γ
T), передаточная функция
формирователя имеет вид:
W
ф
(p) =
p
e
Tp
γ
−
−1
.
Если
γ
=1, то
W
ф
(p) =
p
e
pT−
−1
.
Такой формирователь называют фиксатором нулевого порядка и он
преобразует импульсный сигнал в ступенчатый.
Следовательно, выходной сигнал формирующего звена будет иметь
вид последовательности импульсов с формой f(t), то есть
151
x
и
(t) =
0
() ( )
ф
l
x
lT w t lT
∞
=
−
∑
.
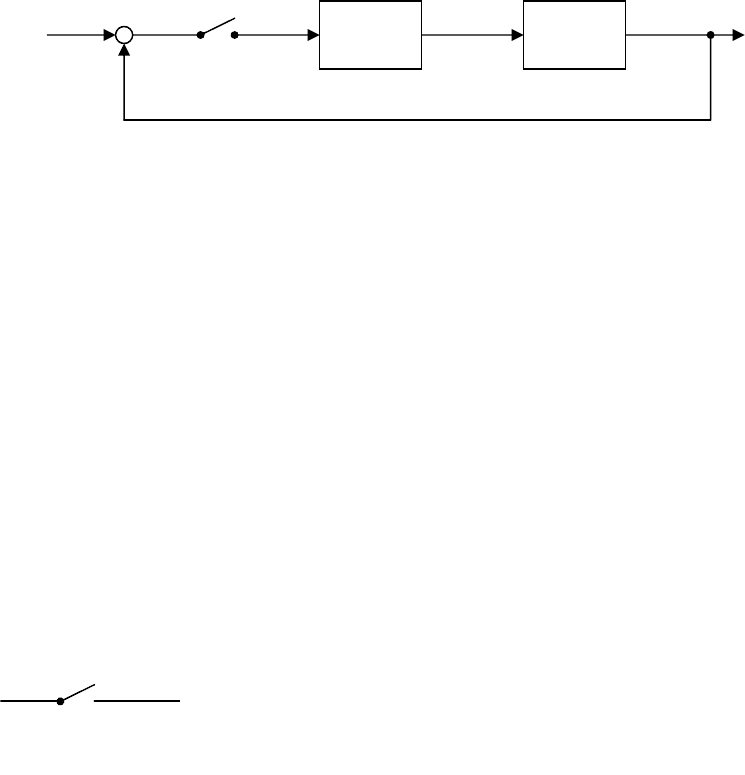
С учетом этого получим эквивалентную схему импульсной системы.
Рис. 16.16
ФЗ и непрерывная часть соединены последовательно и образуют
приведенную НЧ с передаточной функцией
W
фн
(p) = W
ф
(p) W
н
(p).
Важной особенностью ИС является недопустимость перемещения ИЗ
через непрерывное звено в структурных схемах.
16.4. Применение преобразований Фурье и Лапласа для
дискретных сигналов
Рассмотрим идеальное импульсное звено (рис. 6.17).
Пусть при t
<
0 , x(t) = 0, тогда сигнал x
*
(t) равен сумме
модулированных и смещенных единичных импульсных функций
x
*
(t) =
∑
∞
=
−
0
)()(
l
lTtlTx
δ
. (16.1)
Изображение последовательности x
*
(t) определяется формулой
прямого преобразования Лапласа
X
*
(p) =
∫
∞
−
0
*
)( dtetx
pt
. (16.2)
Подставив (16.1) в (16.2) и изменив порядок выполнения операций,
получим
X
*
(p) =
∑
∫
∞
=
∞
−
−
0
0
)()(
l
pt
dtelTtlTx
δ
. (16.3)
Интеграл будет равен
∫
∞
−
−
0
)()( dtelTtlTx
pt
δ
= x(lT) e
-plT
W
ф
(p)
x
x
*
ИИЗ
W
Н
(p)
x
вх
–
x
И
x
вых
x
x
*
ИИЗ
Рис.16.17

152
Здесь учитывается, что подынтегральное выражение всюду равно
нулю, за исключением моментов времени t = lT и интеграл от импульсной
функции равен 1 по определению. Тогда
X
*
(p) =
∑
∞
=
−
0
)(
l
plT
elTx (16.4)
Выражение (16.4) называют дискретным преобразованием Лапласа.
Изображение X
*
(p) соответствует трансцендентной функции от p,
поэтому целесообразно произвести замену переменной:
e
pT
= z. (16.5)
Тогда (16.4) примет вид
X(z) =
∑
∞
=
−
0
)(
l
l
zlTx
. (16.6)
Выражение (16.6) называют z-преобразованием дискретного сигнала.
Преобразование Фурье для сигнала x
*
(t) имеет вид:
X
*
(j
ω
) =
∫
∞
−
0
*
)( dtetx
tj
ω
(16.7)
Аналогичным способом можно получить дискретное преобразование
Фурье:
X
*
( j
ω
) =
0
()
j
lT
l
xlT e
ω
∞
−
=
∑
, (16.8)
где X
*
( j
ω
) – изображение Фурье или спектр.
Важной особенностью спектра дискретного сигнала является его
периодичность по оси частот с периодом
2
И
T
π
ω
= .
Это вытекает из (16.8)
()
2
и
jrlT
j
lT jrl j lT
eeee
ω
ω
ω
πω
−+
−− −
==,
где r = 0, 1, 2,…
Пример 1.
Сигнал x(t) представляет собой единичную функцию, то есть x(t) =
1(t). Тогда дискретная функция имеет вид
x
*
(t) =
∑
∞
=
−⋅
0
)(1
l
lTt
δ
Изображение
