Stewart J. Calculus
Подождите немного. Документ загружается.

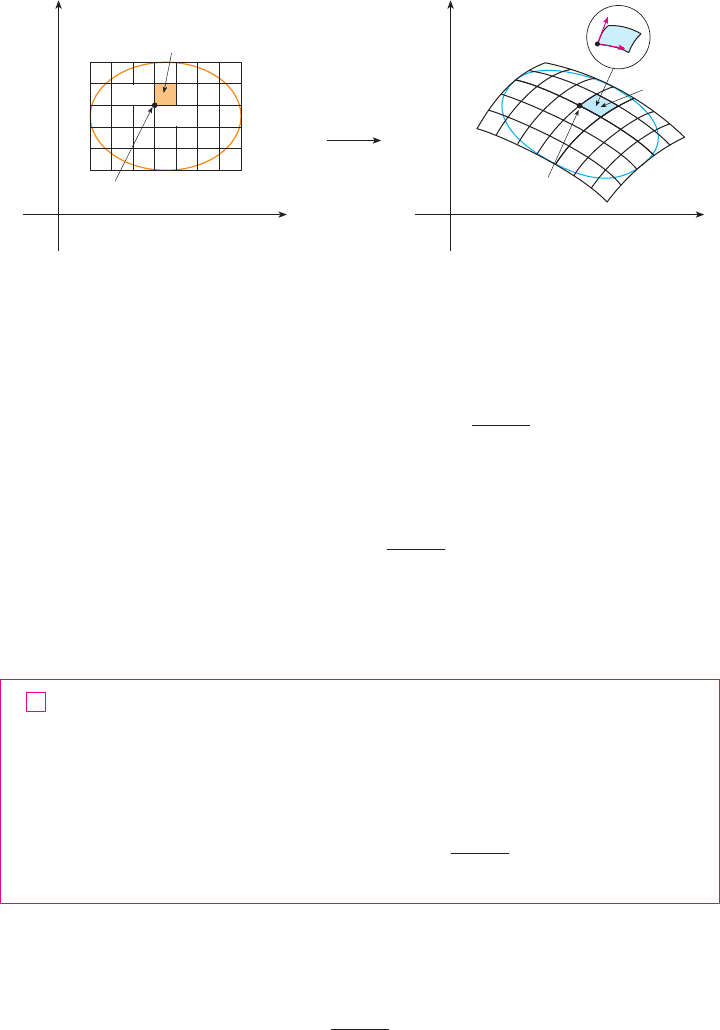
Next we divide a region in the -plane into rectangles and call their images in the
-plane . (See Figure 6.)
Applying the approximation (8) to each we approximate the double integral of
over as follows:
where the Jacobian is evaluated at . Notice that this double sum is a Riemann sum
for the integral
The foregoing argument suggests that the following theorem is true. (A full proof is
given in books on advanced calculus.)
CHANGE OF VARIABLES IN A DOUBLE INTEGRAL Suppose that is a trans-
formation whose Jacobian is nonzero and that maps a region in the -plane onto
a region in the -plane. Suppose that is continuous on and that and are
type I or type II plane regions. Suppose also that is one-to-one, except perhaps
on the boundary of . Then
Theorem 9 says that we change from an integral in and to an integral in and by
expressing and in terms of and and writing
Notice the similarity between Theorem 9 and the one-dimensional formula in Equation 2.
Instead of the derivative , we have the absolute value of the Jacobian, that is,
.
ⱍ
共x, y兲兾共u, v兲
ⱍ
dx兾du
dA 苷
冟
共x, y兲
共u, v兲
冟
du dv
v
uyx
vuyx
yy
R
f 共x, y兲 dA 苷
yy
S
f
(
x共u, v兲, y共u, v兲
)
冟
共x, y兲
共u, v兲
冟
du dv
S
T
SRRfxyR
uvS
C
1
T
9
yy
S
f
(
t共u, v兲, h共u, v兲
)
冟
共x, y兲
共u, v兲
冟
du dv
共u
i
, v
j
兲
⬇
兺
m
i苷1
兺
n
j苷1
f
(
t共u
i
, v
j
兲, h共u
i
, v
j
兲
)
冟
共x, y兲
共u, v兲
冟
u v
yy
R
f 共x, y兲 dA ⬇
兺
m
i苷1
兺
n
j苷1
f 共x
i
, y
j
兲 A
R
fR
ij
,
FIGURE 6
T
0
y
x
R
0
√
u
S
Î√
Îu
(u
i
, √
j
)
S
ij
(x
i
, y
j
)
R
ij
R
ij
xy
S
ij
uvS
1052
||||
CHAPTER 16 MULTIPLE INTEGRALS
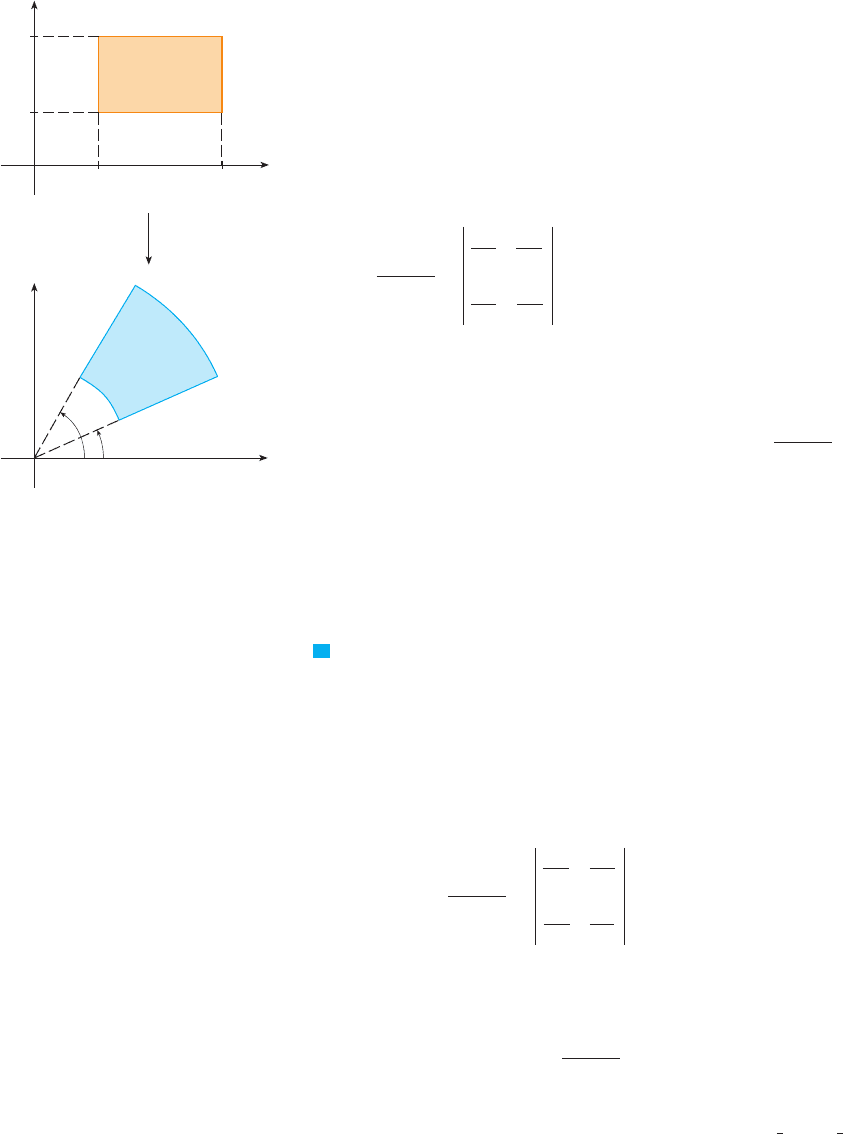
As a first illustration of Theorem 9, we show that the formula for integration in polar
coordinates is just a special case. Here the transformation from the -plane to the
-plane is given by
and the geometry of the transformation is shown in Figure 7. maps an ordinary rectangle
in the -plane to a polar rectangle in the -plane. The Jacobian of is
Thus Theorem 9 gives
which is the same as Formula 16.4.2.
EXAMPLE 2 Use the change of variables , to evaluate the integral
, where is the region bounded by the -axis and the parabolas
and , .
SOLUTION The region is pictured in Figure 2 (on page 1050). In Example 1 we discov-
ered that , where is the square . Indeed, the reason for making
the change of variables to evaluate the integral is that is a much simpler region than .
First we need to compute the Jacobian:
Therefore, by Theorem 9,
M
苷
y
1
0
共2v 4v
3
兲
dv 苷
[
v
2
v
4
]
0
1
苷 2
苷 8
y
1
0
y
1
0
共u
3
v uv
3
兲 du dv 苷 8
y
1
0
[
1
4
u
4
v
1
2
u
2
v
3
]
u苷1
u苷0
dv
yy
R
y dA 苷
yy
S
2uv
冟
共x, y兲
共u, v兲
冟
dA 苷
y
1
0
y
1
0
共2uv兲4共u
2
v
2
兲 du dv
共x, y兲
共u, v兲
苷
ⱍ
x
u
y
u
x
v
y
v
ⱍ
苷
冟
2u
2v
2v
2u
冟
苷 4u
2
4v
2
0
RS
关0, 1兴 关0, 1兴ST 共S 兲 苷 R
R
y 0y
2
苷 4 4x
y
2
苷 4 4xxRxx
R
y dA
y 苷 2uvx 苷 u
2
v
2
V
苷
y
y
b
a
f 共r cos
, r sin
兲
r dr d
yy
R
f 共x, y兲 dx dy 苷
yy
S
f 共r cos
, r sin
兲
冟
共x, y兲
共r,
兲
冟
dr d
共x, y兲
共r,
兲
苷
ⱍ
x
r
y
r
x
y
ⱍ
苷
冟
cos
sin
r sin
r cos
冟
苷 r cos
2
r sin
2
苷 r 0
Txyr
T
y 苷 h共r,
兲 苷 r sin
x 苷 t共r,
兲 苷 r cos
xy
r
T
SECTION 16.9 CHANGE OF VARIABLES IN MULTIPLE INTEGRALS
||||
1053
FIGURE 7
The polar coordinate transformation
0
y
x
¨=∫
r=b
¨=å
r=a
∫
å
R
0
¨
∫
å
r
ab
¨=∫
r=a
¨=å
r=b
S
T
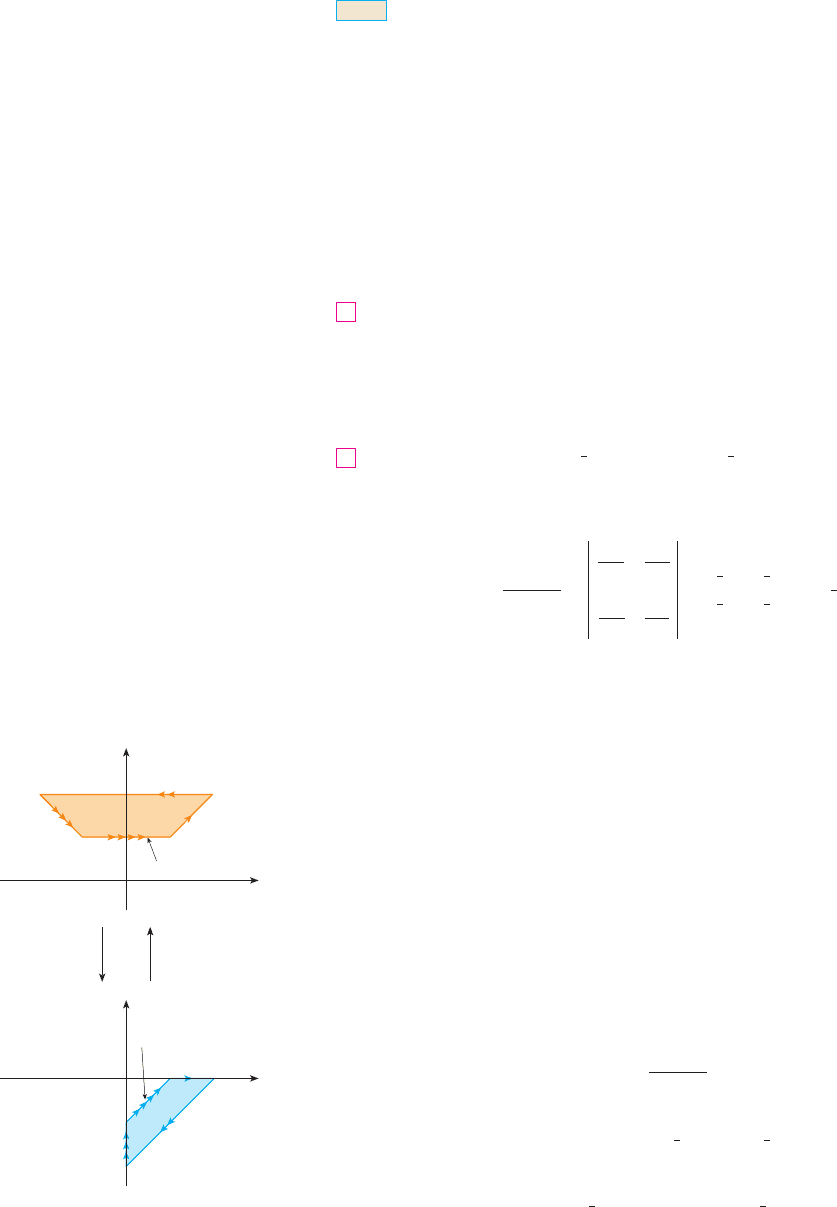
Example 2 was not a very difficult problem to solve because we were given a
suitable change of variables. If we are not supplied with a transformation, then the first step
is to think of an appropriate change of variables. If is difficult to integrate, then the
form of may suggest a transformation. If the region of integration is awkward,
then the transformation should be chosen so that the corresponding region in the -plane
has a convenient description.
EXAMPLE 3
Evaluate the integral , where is the trapezoidal region with
vertices , , , and .
SOLUTION
Since it isn’t easy to integrate , we make a change of variables sug-
gested by the form of this function:
These equations define a transformation from the -plane to the -plane.
Theorem 9 talks about a transformation from the -plane to the -plane. It is
obtained by solving Equations 10 for and :
The Jacobian of is
To find the region in the -plane corresponding to , we note that the sides of lie on
the lines
and, from either Equations 10 or Equations 11, the image lines in the -plane are
Thus the region is the trapezoidal region with vertices , , , and
shown in Figure 8. Since
Theorem 9 gives
M
苷
1
2
y
2
1
共e e
1
兲v
dv 苷
3
4
共e e
1
兲
苷
y
2
1
y
v
v
e
u兾
v
(
1
2
)
du d
v
苷
1
2
y
2
1
[
v
e
u兾
v
]
u苷
v
u苷
v
d
v
yy
R
e
共xy兲兾共xy兲
dA 苷
yy
S
e
u兾
v
冟
共x, y兲
共u,
v
兲
冟
du d
v
S 苷
兵
共u,
v
兲
ⱍ
1
v
2,
v
u
v
其
共1, 1兲
共2, 2兲共2, 2兲共1, 1兲S
v
苷 1u 苷
vv
苷 2u 苷
v
u
v
x y 苷 1x 苷 0x y 苷 2y 苷 0
RRu
v
S
共x, y兲
共u,
v
兲
苷
ⱍ
x
u
y
u
x
v
y
v
ⱍ
苷
冟
1
2
1
2
1
2
1
2
冟
苷
1
2
T
y 苷
1
2
共u
v
兲x 苷
1
2
共u
v
兲
11
yx
xyu
v
T
u
v
xyT
1
v
苷 x yu 苷 x y
10
e
共xy兲兾共xy兲
共0, 1兲共0, 2兲共2, 0兲共1, 0兲
R
xx
R
e
共xy兲兾共xy兲
dA
u
v
S
Rf 共x, y兲
f 共x, y兲
NOTE
1054
||||
CHAPTER 16 MULTIPLE INTEGRALS
FIGURE 8
TT–!
0
√
u
(_2,2) (2,2)
(_1,1) (1,1)
√=2
√=1
u=√u=_√
S
0
y
_1
_2
x
12
x-y=2
x-y=1
R
Openmirrors.com
TRIPLE INTEGRALS
There is a similar change of variables formula for triple integrals. Let be a transfor-
mation that maps a region in -space onto a region in -space by means of the
equations
The Jacobian of is the following determinant:
Under hypotheses similar to those in Theorem 9, we have the following formula for triple
integrals:
EXAMPLE 4 Use Formula 13 to derive the formula for triple integration in spherical
coordinates.
SOLUTION Here the change of variables is given by
We compute the Jacobian as follows:
Since , we have . Therefore
and Formula 13 gives
which is equivalent to Formula 16.8.3. M
yyy
R
f 共x, y, z兲 dV 苷
yyy
S
f 共
sin
cos
,
sin
sin
,
cos
兲
2
sin
d
d
d
冟
共x, y, z兲
共
,
,
兲
冟
苷
ⱍ
2
sin
ⱍ
苷
2
sin
sin
00
苷
2
sin
cos
2
2
sin
sin
2
苷
2
sin
sin
共
sin
2
cos
2
sin
2
sin
2
兲
苷 cos
共
2
sin
cos
sin
2
2
sin
cos
cos
2
兲
苷 cos
冟
sin
sin
sin
cos
cos
cos
cos
sin
冟
sin
冟
sin
cos
sin
sin
sin
sin
sin
cos
冟
共x, y, z兲
共
,
,
兲
苷
ⱍ
sin
cos
sin
sin
cos
sin
sin
sin
cos
0
cos
cos
cos
sin
sin
ⱍ
z 苷
cos
y 苷
sin
sin
x 苷
sin
cos
V
yyy
R
f 共x, y, z兲 dV 苷
yyy
S
f
(
x共u, v, w兲, y共u, v, w兲, z共u, v, w兲
)
冟
共x, y, z兲
共u, v, w兲
冟
du dv dw
13
共x, y, z兲
共u, v, w兲
苷
ⱍ
x
u
y
u
z
u
x
v
y
v
z
v
x
w
y
w
z
w
ⱍ
12
3 3T
z 苷 k共u, v, w兲y 苷 h共u, v, w兲x 苷 t共u, v, w兲
xyzRuvwS
T
SECTION 16.9 CHANGE OF VARIABLES IN MULTIPLE INTEGRALS
||||
1055
1056
||||
CHAPTER 16 MULTIPLE INTEGRALS
;
16. , where is the region bounded by the curves
, , , ; , .
Illustrate by using a graphing calculator or computer to
draw .
17. (a) Evaluate , where is the solid enclosed by the
ellipsoid . Use the transfor-
mation , , .
(b) The earth is not a perfect sphere; rotation has resulted in
flattening at the poles. So the shape can be approximated
by an ellipsoid with km and km.
Use part (a) to estimate the volume of the earth.
18. If the solid of Exercise 17(a) has constant density , find its
moment of inertia about the -axis.
19–23 Evaluate the integral by making an appropriate change of
variables.
19. , where is the parallelogram enclosed by
the lines , , , and
20. , where is the rectangle enclosed by the
lines , , , and
, where is the trapezoidal region
with vertices , , , and
22. , where is the region in the first
quadrant bounded by the ellipse
23. , where is given by the inequality
24. Let be continuous on and let be the triangular
region with vertices , , and . Show that
yy
R
f 共x y兲 dA 苷
y
1
0
uf共u兲 du
共0, 1兲共1, 0兲共0, 0兲
R关0, 1兴f
ⱍ
x
ⱍ
ⱍ
y
ⱍ
1Rxx
R
e
xy
dA
9x
2
4y
2
苷 1
R
xx
R
sin共9x
2
4y
2
兲
dA
共0, 1兲共0, 2兲共2, 0兲共1, 0兲
R
yy
R
cos
冉
y x
y x
冊
dA
21.
x y 苷 3x y 苷 0x y 苷 2x y 苷 0
R
xx
R
共x y兲e
x
2
y
2
dA
3x y 苷 8
3x y 苷 1x 2y 苷 4x 2y 苷 0
R
yy
R
x 2y
3x y
dA
z
k
c 苷 6356a 苷 b 苷 6378
z 苷 c
wy 苷 bvx 苷 au
x
2
兾a
2
y
2
兾b
2
z
2
兾c
2
苷 1
E
xxx
E
dV
R
v 苷 xy
2
u 苷 xyxy
2
苷 2xy
2
苷 1xy 苷 2xy 苷 1
R
xx
R
y
2
dA
1–6 Find the Jacobian of the transformation.
1. ,
2. ,
3. ,
4. ,
5. ,,
6. ,,
7–10 Find the image of the set under the given transformation.
;
8. is the square bounded by the lines , , ,
;,
9. is the triangular region with vertices , , ;
,
10. is the disk given by ; ,
11–16 Use the given transformation to evaluate the integral.
11. , where is the triangular region with
vertices , , and ; ,
12. , where is the parallelogram with
vertices , , , and ;
,
, where is the region bounded by the ellipse
;,
14. , where is the region bounded
by the ellipse ;
,
15. , where is the region in the first quadrant bounded
by the lines and and the hyperbolas ,
;,y 苷
vx 苷 u兾vxy 苷 3
xy 苷 1y 苷 3xy 苷 x
R
xx
R
xy dA
y 苷
s
2
u
s
2兾3
vx 苷
s
2
u
s
2兾3
v
x
2
xy y
2
苷 2
R
xx
R
共x
2
xy y
2
兲
dA
y 苷 3
vx 苷 2u9x
2
4y
2
苷 36
R
xx
R
x
2
dA
13.
y 苷
1
4
共v 3u兲x 苷
1
4
共u v兲
共1, 5兲共3, 1兲共1, 3兲共1, 3兲
R
xx
R
共4x 8y兲 dA
y 苷 u 2
vx 苷 2u v共1, 2兲共2, 1兲共0, 0兲
R
xx
R
共x 3y兲 dA
y 苷 b
vx 苷 auu
2
v
2
1S
y 苷
vx 苷 u
2
共0, 1兲共1, 1兲共0, 0兲S
y 苷 u共1
v
2
兲x 苷 vv 苷 1
v 苷 0u 苷 1u 苷 0S
x 苷 2u 3
v, y 苷 u v
S 苷 兵共u, v兲
ⱍ
0 u 3, 0 v 2其
7.
S
z 苷 u v
2
y 苷 w u
2
x 苷 v w
2
z 苷 w兾uy 苷 v兾wx 苷 u兾v
y 苷 e
st
x 苷 e
st
y 苷 e
r
cos
x 苷 e
r
sin
y 苷 u兾vx 苷 uv
y 苷 u 3vx 苷 5u v
EXERCISES
16.9

REVIEW
CONCEPT CHECK
16
(b) What properties does possess?
(c) What are the expected values of and ?
6. (a) Write the definition of the triple integral of over a
rectangular box .
(b) How do you evaluate ?
(c) How do you define if is a bounded solid
region that is not a box?
(d) What is a type 1 solid region? How do you evaluate
if is such a region?
(e) What is a type 2 solid region? How do you evaluate
if is such a region?
(f) What is a type 3 solid region? How do you evaluate
if is such a region?
7. Suppose a solid object occupies the region and has density
function . Write expressions for each of the following.
(a) The mass
(b) The moments about the coordinate planes
(c) The coordinates of the center of mass
(d) The moments of inertia about the axes
8. (a) How do you change from rectangular coordinates to cylin-
drical coordinates in a triple integral?
(b) How do you change from rectangular coordinates to
spherical coordinates in a triple integral?
(c) In what situations would you change to cylindrical or
spherical coordinates?
9. (a) If a transformation is given by
, what is the Jacobian of ?
(b) How do you change variables in a double integral?
(c) How do you change variables in a triple integral?
Ty 苷 h共u,
v兲
x 苷 t共u,
v兲,T
共x, y, z兲
E
E
xxx
E
f 共x, y, z兲 dV
Exxx
E
f 共x, y, z兲 dV
Exxx
E
f 共x, y, z兲 dV
E
xxx
E
f 共x, y, z兲 dV
xxx
B
f 共x, y, z兲 dV
B
f
YX
f
1. Suppose is a continuous function defined on a rectangle
.
(a) Write an expression for a double Riemann sum of .
If , what does the sum represent?
(b) Write the definition of as a limit.
(c) What is the geometric interpretation of if
? What if takes on both positive and negative
values?
(d) How do you evaluate ?
(e) What does the Midpoint Rule for double integrals say?
(f) Write an expression for the average value of .
2. (a) How do you define if is a bounded region
that is not a rectangle?
(b) What is a type I region? How do you evaluate
if is a type I region?
(c) What is a type II region? How do you evaluate
if is a type II region?
(d) What properties do double integrals have?
3. How do you change from rectangular coordinates to polar coor-
dinates in a double integral? Why would you want to make the
change?
4. If a lamina occupies a plane region and has density function
, write expressions for each of the following in terms of
double integrals.
(a) The mass
(b) The moments about the axes
(c) The center of mass
(d) The moments of inertia about the axes and the origin
5. Let be a joint density function of a pair of continuous
random variables and .
(a) Write a double integral for the probability that lies
between and and lies between and .dcYba
X
YX
f
共x, y兲
D
D
xx
D
f 共x, y兲 dA
D
xx
D
f 共x, y兲 dA
D
xx
D
f 共x, y兲 dA
f
xx
R
f 共x, y兲 dA
ff 共x, y兲 0
xx
R
f 共x, y兲 dA
xx
R
f 共x, y兲 dA
f 共x, y兲 0
f
R 苷 关a, b兴 关c, d 兴
f
Determine whether the statement is true or false. If it is true, explain why.
If it is false, explain why or give an example that disproves the statement.
1.
2.
3.
4.
y
1
1
y
1
0
e
x
2
y
2
sin y dx dy 苷 0
y
2
1
y
4
3
x
2
e
y
dy dx 苷
y
2
1
x
2
dx
y
4
3
e
y
dy
y
1
0
y
x
0
s
x y
2
dy dx 苷
y
x
0
y
1
0
s
x y
2
dx dy
y
2
1
y
6
0
x
2
sin共x y兲 dx dy 苷
y
6
0
y
2
1
x
2
sin共x y兲 dy dx
5. If is the disk given by , then
6.
7.
The integral
represents the volume enclosed by the cone
and the plane .
8. The integral represents the moment of
inertia about the -axis of a solid with constant density .kEz
xxx
E
kr
3
dz dr d
z 苷 2
z 苷
s
x
2
y
2
y
2
0
y
2
0
y
2
r
dz dr d
y
4
1
y
1
0
(
x
2
s
y
)
sin共x
2
y
2
兲
dx dy 9
yy
D
s
4 x
2
y
2
dA 苷
16
3
x
2
y
2
4D
TRUE-FALSE QUIZ
CHAPTER 16 REVIEW
||||
1057
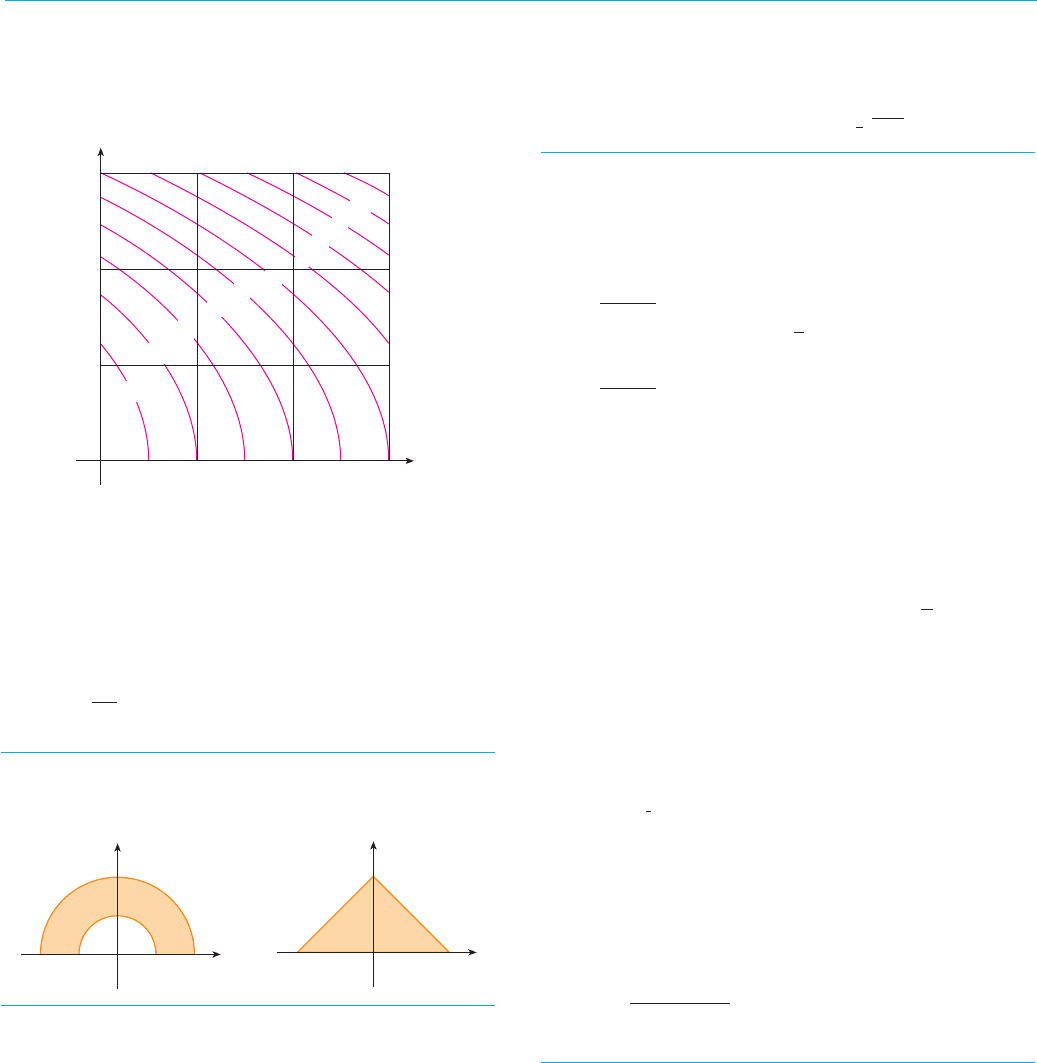
1. A contour map is shown for a function on the square
. Use a Riemann sum with nine terms to
estimate the value of . Take the sample points to
be the upper right corners of the squares.
2. Use the Midpoint Rule to estimate the integral in Exercise 1.
3–8 Calculate the iterated integral.
3. 4.
5. 6.
7. 8.
9–10 Write as an iterated integral, where is the
region shown and f is an arbitrary continuous function on .
9. 10.
11. Describe the region whose area is given by the integral
12. Describe the solid whose volume is given by the integral
and evaluate the integral.
y
兾2
0
y
兾2
0
y
2
1
2
sin
d
d
d
y
兾2
0
y
sin 2
0
r dr d
0
4
y
x
R
4_4
0
42_2_4
y
x
R
2
4
R
R
xx
R
f 共x, y兲 dA
y
1
0
y
y
0
y
1
x
6xyz dz dx dy
y
0
y
1
0
y
s
1y
2
0
y sin x dz dy dx
y
1
0
y
e
x
x
3xy
2
dy dx
y
1
0
y
x
0
cos共x
2
兲 dy dx
y
1
0
y
1
0
ye
xy
dx dy
y
2
1
y
2
0
共y 2xe
y
兲 dx dy
y
0
1
1
123
2
3
2
3
4
5
8
9
10
6
7
x
xx
R
f 共x, y兲 dA
R 苷 关0, 3兴 关0, 3兴
f
13–14 Calculate the iterated integral by first reversing the order of
integration.
13. 14.
15–28 Calculate the value of the multiple integral.
15. , where ,
16. , where ,
17. ,
where is bounded by , ,
18. , where is the triangular region with
vertices , , and
19. , where is the region in the first quadrant bounded by
the parabolas and
20. , where is the region in the first quadrant that lies
above the hyperbola and the line and below the
line
21. , where is the region in the first
quadrant bounded by the lines and and the
circle
22. , where is the region in the first quadrant that lies
between the circles and
23. , where
,,
24. , where is the solid tetrahedron with vertices
, , , and
25. , where is bounded by the paraboloid
and the plane
26. , where is bounded by the planes , ,
and the cylinder in the first octant
27. , where lies above the plane , below the plane
, and inside the cylinder
28. , where is the solid hemisphere that
lies above the -plane and has center the origin and radius 1
29–34 Find the volume of the given solid.
29. Under the paraboloid and above the rectangle
30. Under the surface and above the triangle in the
-plane with vertices , , and 共4, 0兲共2, 1兲共1, 0兲xy
z 苷 x
2
y
R 苷 关0, 2兴 关1, 4兴
z 苷 x
2
4y
2
xy
H
xxx
H
z
3
s
x
2
y
2
z
2
dV
x
2
y
2
苷 4z 苷 y
z 苷 0E
xxx
E
yz dV
y
2
z
2
苷 1x y 苷 2
z 苷 0y 苷 0E
xxx
E
z dV
x 苷 0x 苷 1 y
2
z
2
Exxx
E
y
2
z
2
dV
共0, 0, 1兲共0, 1, 0兲
(
1
3
, 0, 0
)
共0, 0, 0兲
T
xxx
T
xy dV
0 z x y其0 y xE 苷 兵共x, y, z兲
ⱍ
0 x 3
xxx
E
xy dV
x
2
y
2
苷 2x
2
y
2
苷 1
D
xx
D
x dA
x
2
y
2
苷 9
y 苷
s
3
xy 苷 0
D
xx
D
共x
2
y
2
兲
3兾2
dA
y 苷 2
y 苷 xxy 苷 1
D
xx
D
y dA
x 苷 8 y
2
x 苷 y
2
Dxx
D
y dA
共0, 1兲共1, 1兲共0, 0兲
D
yy
D
1
1 x
2
dA
x 苷 1y 苷 0y 苷
s
x
D
yy
D
y
1 x
2
dA
y
2
x y 2其D 苷 兵共x, y兲
ⱍ
0 y 1xx
D
xy
dA
0 y 3其R 苷 兵共x, y兲
ⱍ
0 x 2xx
R
ye
xy
dA
y
1
0
y
1
s
y
ye
x
2
x
3
dx dy
y
1
0
y
1
x
cos共y
2
兲
dy dx
EXERCISES
1058
||||
CHAPTER 16 MULTIPLE INTEGRALS

44. A lamp has three bulbs, each of a type with average lifetime
800 hours. If we model the probability of failure of the
bulbs by an exponential density function with mean 800,
find the probability that all three bulbs fail within a total of
1000 hours.
45. Rewrite the integral
as an iterated integral in the order .
46. Give five other iterated integrals that are equal to
47. Use the transformation , to evaluate
, where is the square with vertices
, , , and .
48. Use the transformation , , to
find the volume of the region bounded by the surface
and the coordinate planes.
49. Use the change of variables formula and an appropriate trans-
formation to evaluate , where is the square with
vertices , , , and .
50. The Mean Value Theorem for double integrals says that
if is a continuous function on a plane region that is of
type I or II, then there exists a point in such that
Use the Extreme Value Theorem (15.7.8) and Property
16.3.11 of integrals to prove this theorem. (Use the proof of
the single-variable version in Section 6.5 as a guide.)
51. Suppose that is continuous on a disk that contains the
point . Let be the closed disk with center and
radius . Use the Mean Value Theorem for double integrals
(see Exercise 50) to show that
52. (a) Evaluate , where is an integer and
is the region bounded by the circles with center the
origin and radii and , .
(b) For what values of does the integral in part (a) have a
limit as ?
(c) Find , where is the region
bounded by the spheres with center the origin and radii
and , .
(d) For what values of does the integral in part (c) have a
limit as ?r l 0
n
0
r
R
R
r
E
yyy
E
1
共x
2
y
2
z
2
兲
n兾2
dV
r l 0
n
0
r
R
Rr
D
n
yy
D
1
共x
2
y
2
兲
n兾2
dA
lim
r
l
0
1
r
2
yy
D
r
f 共x, y兲 dA 苷 f 共a, b兲
r
共a, b兲D
r
共a, b兲
f
yy
D
f 共x, y兲 dA 苷 f 共x
0
, y
0
兲
A共D兲
D共x
0
, y
0
兲
Df
共1, 1兲共2, 0兲共1, 1兲共0, 0兲
R
xx
R
xy dA
s
x
s
y
s
z
苷 1
z 苷
w
2
y 苷 v
2
x 苷 u
2
共1, 3兲共2, 2兲共1, 1兲共0, 2兲
R
xx
R
共x y兲兾共 x y兲 dA
v 苷 x yu 苷 x y
y
2
0
y
y
3
0
y
y
2
0
f 共x, y, z兲 dz dx dy
dx dy dz
y
1
1
y
1
x
2
y
1y
0
f 共x, y, z兲 dz dy dx
31. The solid tetrahedron with vertices , , ,
and
32. Bounded by the cylinder and the planes
and
33. One of the wedges cut from the cylinder by
the planes and
34. Above the paraboloid and below the half-cone
35. Consider a lamina that occupies the region bounded by
the parabola and the coordinate axes in the first
quadrant with density function .
(a) Find the mass of the lamina.
(b) Find the center of mass.
(c) Find the moments of inertia and radii of gyration about
the - and -axes.
36. A lamina occupies the part of the disk that lies
in the first quadrant.
(a) Find the centroid of the lamina.
(b) Find the center of mass of the lamina if the density func-
tion is .
37. Find the centroid of a right circular cone with height
and base radius . (Place the cone so that its base is in the
-plane with center the origin and its axis along the positive
-axis.)
38. Find the moment of inertia of the cone in Exercise 37 about
its axis (the -axis).
39. Use polar coordinates to evaluate
40. Use spherical coordinates to evaluate
;
41. If is the region bounded by the curves and
, find the approximate value of the integral .
(Use a graphing device to estimate the points of intersection
of the curves.)
42. Find the center of mass of the solid tetrahedron with vertices
, , , and density function
.
43. The joint density function for random variables and is
(a) Find the value of the constant .
(b) Find .
(c) Find .P共X Y 1兲
P共X 2, Y 1兲
C
f 共x, y兲 苷
再
C共x y兲
0
if 0 x 3, 0 y 2
otherwise
YX
共x, y, z兲 苷 x
2
y
2
z
2
共0, 0, 3兲共0, 2, 0兲共1, 0, 0兲共0, 0, 0兲
CAS
xx
D
y
2
dAy 苷 e
x
y 苷 1 x
2
D
y
2
2
y
s
4y
2
0
y
s
4x
2
y
2
s
4x
2
y
2
y
2
s
x
2
y
2
z
2
dz dx dy
y
3
0
y
s
9x
2
s
9x
2
共x
3
xy
2
兲 dy dx
z
z
xy
a
h
共x, y兲 苷 xy
2
x
2
y
2
a
2
yx
共x, y兲 苷 y
x 苷 1 y
2
D
z 苷
s
x
2
y
2
z 苷 x
2
y
2
z 苷 mxz 苷 0
x
2
9y
2
苷 a
2
y z 苷 3
z 苷 0x
2
y
2
苷 4
共2, 2, 0兲
共0, 2, 0兲共0, 0, 1兲共0, 0, 0兲
CHAPTER 16 REVIEW
||||
1059

1060
1. If denotes the greatest integer in , evaluate the integral
where .
2. Evaluate the integral
where max means the larger of the numbers and .
3. Find the average value of the function on the interval .
4. If , , and are constant vectors, is the position vector , and is given by
the inequalities , , , show that
5. The double integral is an improper integral and could be defined as
the limit of double integrals over the rectangle as . But if we expand the
integrand as a geometric series, we can express the integral as the sum of an infinite series.
Show that
6. Leonhard Euler was able to find the exact sum of the series in Problem 5. In 1736 he proved
that
In this problem we ask you to prove this fact by evaluating the double integral in Problem 5.
Start by making the change of variables
This gives a rotation about the origin through the angle . You will need to sketch the
corresponding region in the -plane.
[Hint: If, in evaluating the integral, you encounter either of the expressions
or , you might like to use the identity
and the corresponding identity for .]
7. (a) Show that
(Nobody has ever been able to find the exact value of the sum of this series.)
y
1
0
y
1
0
y
1
0
1
1 xyz
dx dy dz 苷
兺
n苷1
1
n
3
sin
cos
苷 sin共共
兾2兲
兲
共cos
兲兾共1 sin
兲共1 sin
兲兾cos
uv
兾4
y 苷
u v
s
2
x 苷
u v
s
2
兺
n苷1
1
n
2
苷
2
6
y
1
0
y
1
0
1
1 xy
dx dy 苷
兺
n苷1
1
n
2
t l 1
关0, t兴 关0, t兴
y
1
0
y
1
0
1
1 xy
dx dy
yyy
E
共a ⴢ r兲共b ⴢ r兲共c ⴢ r兲 dV 苷
共
兲
2
8
ⱍ
a ⴢ 共b c兲
ⱍ
0 c ⴢ r
0 b ⴢ r
0 a ⴢ r
Ex i y j z krcba
[0, 1]f 共x兲 苷
x
1
x
cos共t
2
兲
dt
y
2
x
2
兵x
2
, y
2
其
y
1
0
y
1
0
e
max兵x
2
, y
2
其
dy dx
R 苷 兵共x, y兲
ⱍ
1 x 3, 2 y 5其
yy
R
冀x y冁 dA
x冀x冁
PROBLEMS PLUS

1061
(b) Show that
Use this equation to evaluate the triple integral correct to two decimal places.
8. Show that
by first expressing the integral as an iterated integral.
9. (a) Show that when Laplace’s equation
is written in cylindrical coordinates, it becomes
(b) Show that when Laplace’s equation is written in spherical coordinates, it becomes
10. (a) A lamina has constant density and takes the shape of a disk with center the origin and
radius . Use Newton’s Law of Gravitation (see Section 14.4) to show that the magnitude
of the force of attraction that the lamina exerts on a body with mass located at the point
on the positive -axis is
[Hint: Divide the disk as in Figure 4 in Section 16.4 and first compute the vertical com-
ponent of the force exerted by the polar subrectangle .]
(b) Show that the magnitude of the force of attraction of a lamina with density that occupies
an entire plane on an object with mass located at a distance from the plane is
Notice that this expression does not depend on .
11. If is continuous, show that
y
x
0
y
y
0
y
z
0
f 共t兲 dt dz dy 苷
1
2
y
x
0
共x t兲
2
f 共t兲 dt
f
d
F 苷 2
Gm
dm
R
ij
F 苷 2
Gm
d
冉
1
d
1
s
R
2
d
2
冊
z共0, 0, d 兲
m
R
2
u
2
2
u
cot
2
u
1
2
2
u
2
1
2
sin
2
2
u
2
苷 0
2
u
r
2
1
r
u
r
1
r
2
2
u
2
2
u
z
2
苷 0
2
u
x
2
2
u
y
2
2
u
z
2
苷 0
y
0
arctan
x arctan x
x
dx 苷
2
ln
y
1
0
y
1
0
y
1
0
1
1 xyz
dx dy dz 苷
兺
n苷1
共1兲
n1
n
3
PROBLEMS PLUS
