Stewart J. Calculus

By applying the Mean Value Theorem to on the interval , we ﬁnd that there is a

number between and such that

that is,

Thus we have

(since )

Therefore, by Deﬁnition 1,

We recognize this expression as being equal to

by the deﬁnition of a deﬁnite integral. This integral exists because the function

is continuous. Thus we have proved the following theorem:

THE ARC LENGTH FORMULA If is continuous on , then the length of

the curve , , is

If we use Leibniz notation for derivatives, we can write the arc length formula as

follows:

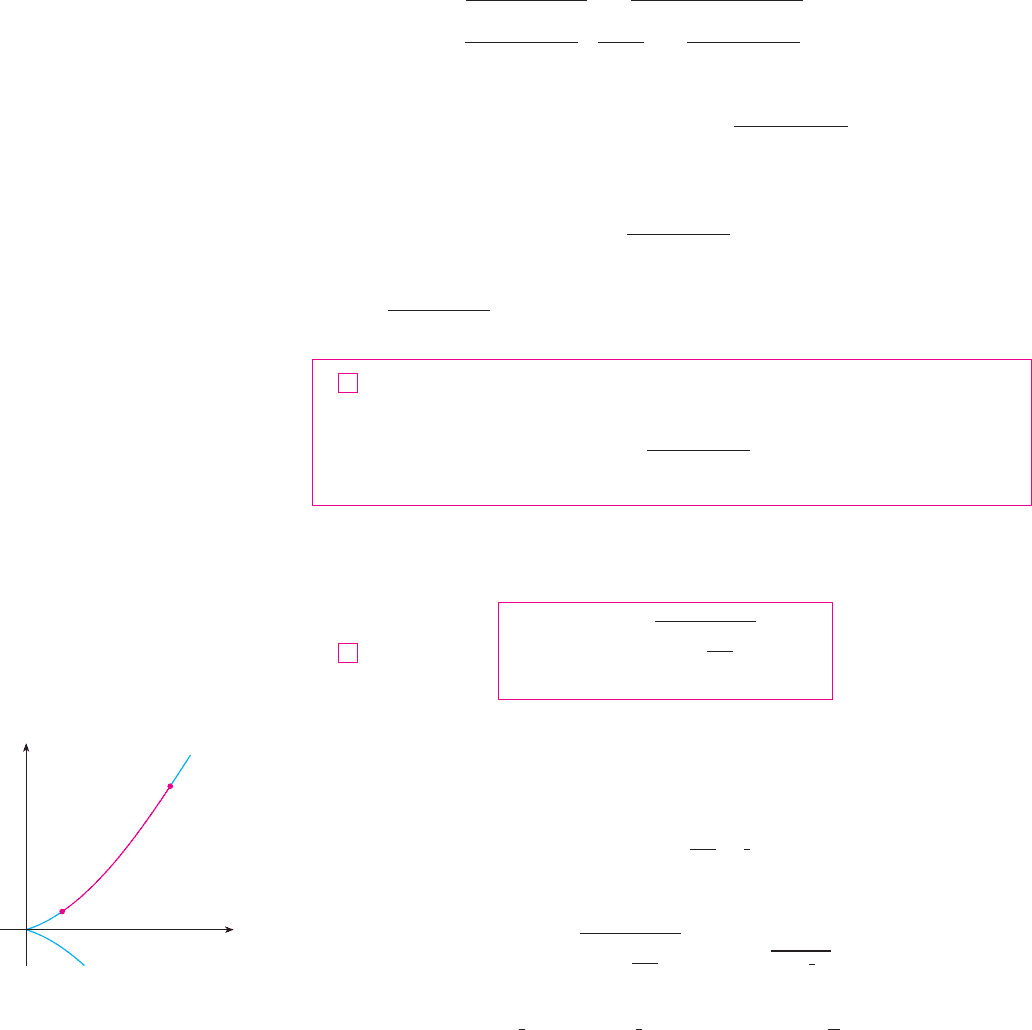
EXAMPLE 1 Find the length of the arc of the semicubical parabola between the

points and . (See Figure 5.)

SOLUTION For the top half of the curve we have

and so the arc length formula gives

If we substitute , then . When , ; when , .u ! 10x ! 4u !

13

4

x ! 1du !

9

4

dxu ! 1 "

9

4

x

L !

y

4

1

'

1 "

(

dy

dx

)

2

dx !

y

4

1

s

1 "

9

4

x

dx

dy

dx

!

3

2

x

1*2

y ! x

3*2

"4, 8#"1, 1#

y

2

! x

3

L !

y

b

a

'

1 "

(

dy

dx

)

2

dx

3

L !

y

b

a

s

1 " % f $"x#&

2

dx

a & x & by ! f "x#

%a, b&f $

2

t"x# !

s

1 " % f $"x#&

2

y

b

a

s

1 " % f $"x#&

2

dx

! lim

n

l

%

$

n

i!1

s

1 " % f $"x

i

*

#&

2

#xL ! lim

n

l

%

$

n

i!1

!

P

i!1

P

i

!

#x ' 0!

s

1 " % f $"x

i

*

#&

2

#x!

s

1 " [ f $"x

i

*

#&

2

s

"#x#

2

!

s

"#x#

2

" % f $"x

i

*

# #x&

2

!

P

i!1

P

i

!

s

"#x#

2

" "#y

i

#

2

#y

i

! f $"x

i

*

# #x

f "x

i

# ! f "x

i!1

# ! f $"x

i

*

#"x

i

! x

i!1

#

x

i

x

i!1

x

i

*

%x

i!1

, x

i

&f

562

|| ||

CHAPTER 9 FURTHER APPLICATIONS OF INTEGRATION

(4,8)

F I G U R E 5

0

x

y

(1,1)

¥=˛

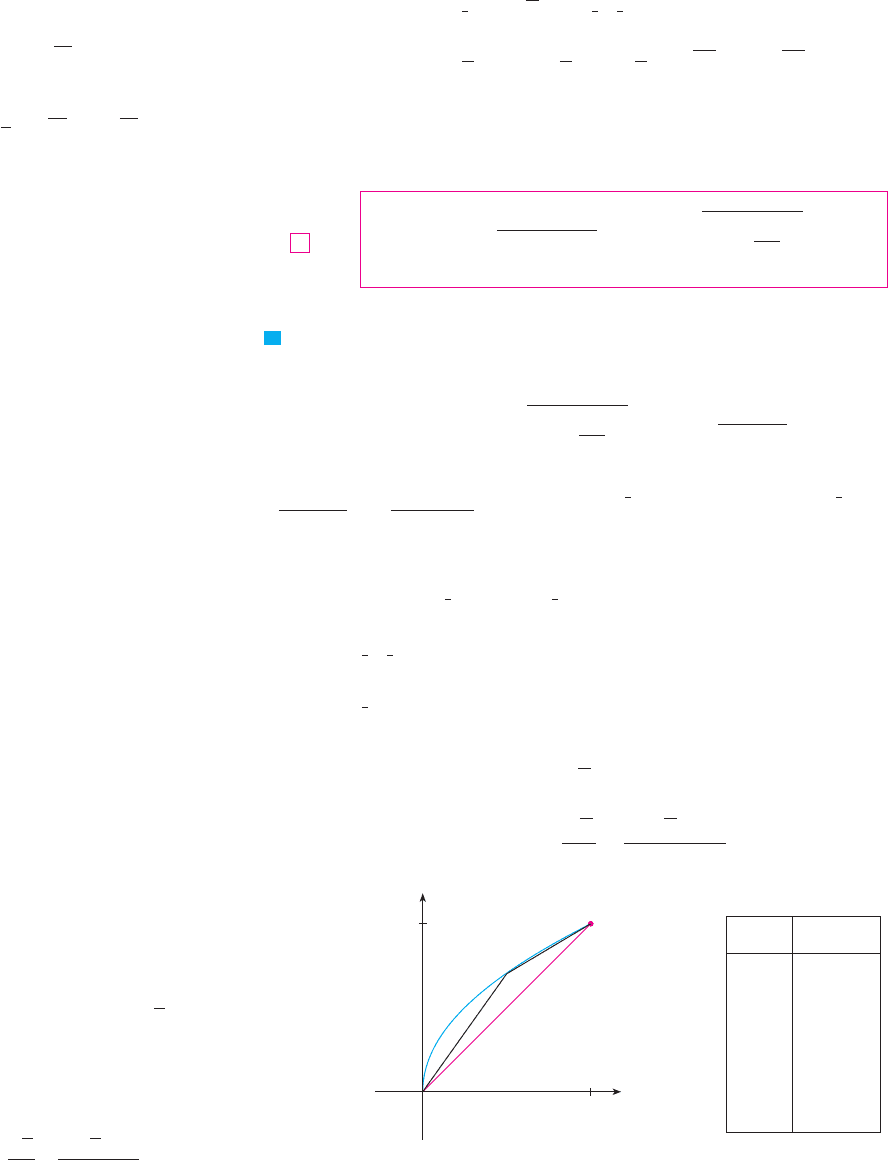
Therefore

M

If a curve has the equation , , and is continuous, then by inter-

changing the roles of and in Formula 2 or Equation 3, we obtain the following formula

for its length:

EXAMPLE 2 Find the length of the arc of the parabola from to .

SOLUTION Since , we have , and Formula 4 gives

We make the trigonometric substitution , which gives and

. When , , so ; when ,

, so , say. Thus

(from Example 8 in Section 8.2)

(We could have used Formula 21 in the Table of Integrals.) Since , we have

, so and

M

0

x

y

1

x=¥

F I G U R E 6

L !

s

5

2

"

ln

(

s

5

" 2

)

4

sec

(

!

s

5

sec

2

(

! 1 " tan

2

(

! 5

tan

(

! 2

!

1

4

(

sec

(

tan

(

" ln

!

sec

(

" tan

(

!

)

!

1

2

!

1

2

[

sec

)

tan

)

" ln

!

sec

)

" tan

)

!

]

0

(

L !

y

(

0

sec

)

!

1

2

sec

2

)

d

)

!

1

2

y

(

0

sec

3

)

d

)

! tan

!1

2 !

(

tan

)

! 2

y ! 1

)

! 0tan

)

! 0y ! 0

s

1 " 4y

2

!

s

1 " tan

2

)

! sec

)

dy !

1

2

sec

2

)

d

)

y !

1

2

tan

)

L !

y

1

0

'

1 "

(

dx

dy

)

2

dy !

y

1

0

s

1 " 4y

2

dy

dx*dy ! 2yx ! y

2

"1, 1#"0, 0#y

2

! x

V

L !

y

d

c

s

1 " %t$"y#&

2

dy !

y

d

c

'

1 "

(

dx

dy

)

2

dy

4

yx

t$"y#c & y & dx ! t"y#

!

1

27

(

80

s

10

! 13

s

13

)

!

8

27

[

10

3*2

!

(

13

4

)

3*2

]

L !

4

9

y

10

13*4

s

u

du !

4

9

!

2

3

u

3*2

]

13*4

10

SECTION 9.1 ARC LENGTH

|| ||

563

N As a check on our answer to Example 1, notice

from Figure 5 that the arc length ought to be

slightly larger than the distance from to

, which is

According to our calculation in Example 1, we

have

Sure enough, this is a bit greater than the length

of the line segment.

L !

1

27

(

80

s

10

! 13

s

13

)

+ 7.633705

s

58

+ 7.615773

"4, 8#

"1, 1#

N Figure 6 shows the arc of the parabola whose

length is computed in Example 2, together with

polygonal approximations having and

line segments, respectively. For

the approximate length is , the diago-

nal of a square. The table shows the approxima-

tions that we get by dividing into

equal subintervals. Notice that each time we

double the number of sides of the polygon, we

get closer to the exact length, which is

L !

s

5

2

"

ln

(

s

5

" 2

)

4

+ 1.478943

n%0, 1&L

n

L

1

!

s

2

n ! 1n ! 2

n ! 1

n

1 1.414

2 1.445

4 1.464

8 1.472

16 1.476

32 1.478

64 1.479

L

n

Because of the presence of the square root sign in Formulas 2 and 4, the calculation of

an arc length often leads to an integral that is very difﬁcult or even impossible to evaluate

explicitly. Thus we sometimes have to be content with ﬁnding an approximation to the

length of a curve, as in the following example.

EXAMPLE 3

(a) Set up an integral for the length of the arc of the hyperbola from the

point to the point .

(b) Use Simpson’s Rule with to estimate the arc length.

SOLUTION

(a) We have

and so the arc length is

(b) Using Simpson’s Rule (see Section 8.7) with , , , , and

, we have

M

THE ARC LENGTH FUNCTION

We will ﬁnd it useful to have a function that measures the arc length of a curve from a par-

ticular starting point to any other point on the curve. Thus if a smooth curve has the

equation , , let be the distance along from the initial point

to the point . Then is a function, called the arc length function, and,

by Formula 2,

(We have replaced the variable of integration by so that does not have two meanings.)

We can use Part 1 of the Fundamental Theorem of Calculus to differentiate Equation 5

(since the integrand is continuous):

ds

dx

!

s

1 " % f $"x#&

2

!

'

1 "

(

dy

dx

)

2

6

xt

s"x# !

y

x

a

s

1 " % f $"t#&

2

dt

5

sQ"x, f "x##P

0

"a, f "a##

Cs"x#a & x & by ! f "x#

C

+ 1.1321

+

#x

3

% f "1# " 4 f "1.1# " 2 f "1.2# " 4 f "1.3# " * * * " 2 f "1.8# " 4 f "1.9# " f "2#&

L !

y

2

1

'

1 "

1

x

4

dx

f "x# !

s

1 " 1*x

4

#x ! 0.1n ! 10b ! 2a ! 1

L !

y

2

1

'

1 "

(

dy

dx

)

2

dx !

y

2

1

'

1 "

1

x

4

dx !

y

2

1

s

x

4

" 1

x

2

dx

dy

dx

! !

1

x

2

y !

1

x

n ! 10

(

2,

1

2

)

"1, 1#

xy ! 1

V

564

|| ||

CHAPTER 9 FURTHER APPLICATIONS OF INTEGRATION

N Checking the value of the deﬁnite integral

with a more accurate approximation produced by

a computer algebra system, we see that the

approximation using Simpson’s Rule is accurate

to four decimal places.

Equation 6 shows that the rate of change of with respect to is always at least 1 and is

equal to 1 when , the slope of the curve, is 0. The differential of arc length is

and this equation is sometimes written in the symmetric form

The geometric interpretation of Equation 8 is shown in Figure 7. It can be used as a

mnemonic device for remembering both of the Formulas 3 and 4. If we write , then

from Equation 8 either we can solve to get (7), which gives (3), or we can solve to get

which gives (4).

EXAMPLE 4 Find the arc length function for the curve taking

as the starting point.

SOLUTION If , then

Thus the arc length function is given by

For instance, the arc length along the curve from to is

M

s"3# ! 3

2

"

1

8

ln 3 ! 1 ! 8 "

ln 3

8

+ 8.1373

"3, f "3##"1, 1#

! x

2

"

1

8

ln x ! 1

!

y

x

1

(

2t !

1

8t

)

dt ! t

2

"

1

8

ln t

]

1

x

s"x# !

y

x

1

s

1 " % f $"t#&

2

dt

s

1 " % f $"x#&

2

! 2x "

1

8x

! 4x

2

"

1

2

"

1

64x

2

!

(

2x "

1

8x

)

2

1 " % f $"x#&

2

! 1 "

(

2x !

1

8x

)

2

! 1 " 4x

2

!

1

2

"

1

64x

2

f $"x# ! 2x !

1

8x

f "x# ! x

2

!

1

8

ln x

P

0

"1, 1#y ! x

2

!

1

8

ln x

V

ds !

'

1 "

(

dx

dy

)

2

dy

L !

x ds

"ds#

2

! "dx#

2

" "dy#

2

8

ds !

'

1 "

(

dy

dx

)

2

dx

7

f $"x#

xs

SECTION 9.1 ARC LENGTH

|| ||

565

F I G U R E 7

0

x

y

dx

ds

dy

Îs Îy

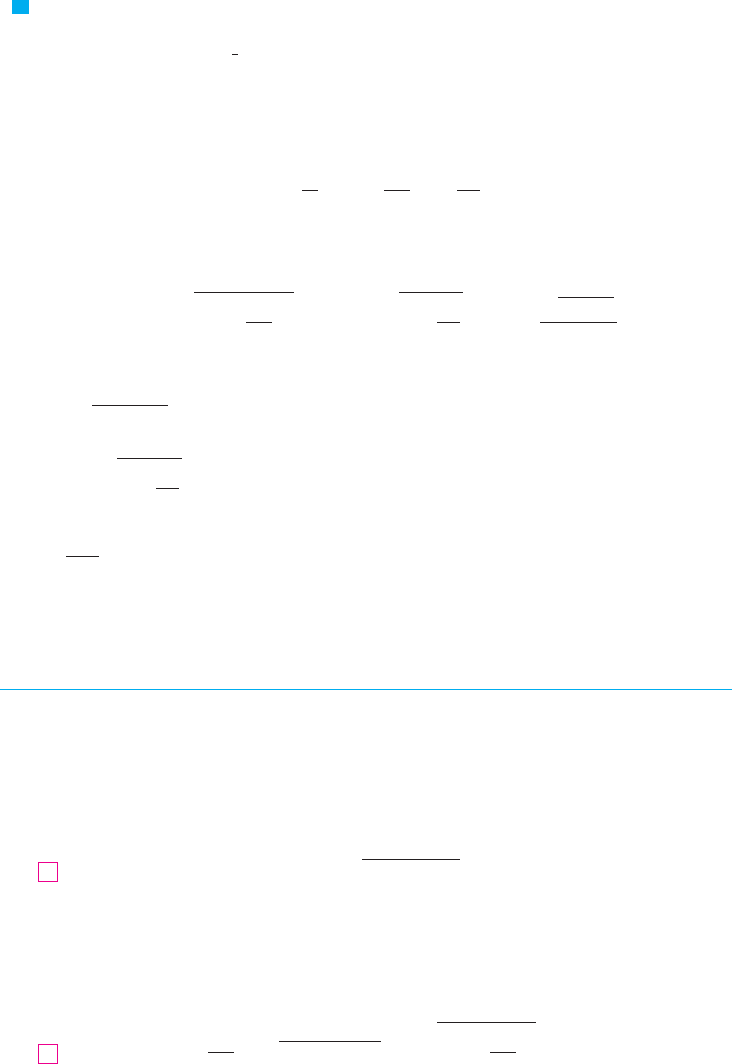
F I G U R E 9

F I G U R E 8

P¸

1

8

y=≈- lnx

1

8

0 x

y

1

0 x

y

1 x

1

s(x)=≈+ lnx-1

s(x)

566

|| ||

CHAPTER 9 FURTHER APPLICATIONS OF INTEGRATION

15. ,

16.

17.

,

18. , ,

;

19–20 Find the length of the arc of the curve from point to

point .

19. , ,

20. , ,

;

21–22 Graph the curve and visually estimate its length. Then ﬁnd

its exact length.

21. ,

22. ,

23–26 Use Simpson’s Rule with to estimate the arc

length of the curve. Compare your answer with the value of the

integral produced by your calculator.

23. ,

24. ,

25. ,

26. ,

1 & x & 3y ! x ln x

0 & x &

+

*3y ! sec x

1 & y & 2x ! y "

s

y

0 & x & 5y ! xe

!x

n ! 10

1

2

& x & 1

y !

x

3

6

"

1

2x

1 & x & 3y !

2

3

"x

2

! 1#

3*2

Q"8, 8#P"1, 5#x

2

! " y ! 4#

3

Q

(

1,

1

2

)

P

(

!1,

1

2

)

y !

1

2

x

2

Q

P

a ' 0a & x & by ! ln

(

e

x

" 1

e

x

! 1

)

0 & x & 1y ! e

x

y !

s

x ! x

2

" sin

!1

(

s

x

)

0 & x &

1

2

y ! ln"1 ! x

2

#

1. Use the arc length formula (3) to ﬁnd the length of the curve

, . Check your answer by noting that

the curve is a line segment and calculating its length by the

distance formula.

2. Use the arc length formula to ﬁnd the length of the curve

, . Check your answer by noting that

the curve is part of a circle.

3–6 Set up, but do not evaluate, an integral for the length of the

curve.

3. ,

4. ,

5. ,

6.

7–18 Find the length of the curve.

,

8.

, ,

9. ,

10. ,

,

12. ,

,

14. , 0 & x & 1y ! 3 "

1

2

cosh 2x

0 & x &

+

*4y ! ln"sec x#

13.

0 & x &

+

*3y ! ln"cos x#

1 & y & 9x !

1

3

s

y

"y ! 3#

11.

1 & y & 2x !

y

4

8

"

1

4y

2

1 & x & 2y !

x

5

6

"

1

10x

3

y ' 00 & x & 2y

2

! 4"x " 4#

3

0 & x & 1y ! 1 " 6x

3* 2

7.

x

2

a

2

"

y

2

b

2

! 1

1 & y & 4x ! y " y

3

0 & x & 1y ! xe

!x

2

0 & x & 2

+

y ! cos x

0 & x & 1y !

s

2 ! x

2

!1 & x & 3y ! 2x ! 5

E X E R C I S E S

9.1

N Figure 8 shows the interpretation of the arc

length function in Example 4. Figure 9 shows the

graph of this arc length function. Why is

negative when is less than ?1x

s"x#

SECTION 9.1 ARC LENGTH

|| ||

567

the distance traveled by the prey from the time it is dropped

until the time it hits the ground. Express your answer correct

to the nearest tenth of a meter.

38. The Gateway Arch in St. Louis (see the photo on page 465)

was constructed using the equation

for the central curve of the arch, where and are measured

in meters and . Set up an integral for the length

of the arch and use your calculator to estimate the length

correct to the nearest meter.

A manufacturer of corrugated metal rooﬁng wants to produce

panels that are 28 in. wide and 2 in. thick by processing ﬂat

sheets of metal as shown in the ﬁgure. The proﬁle of the roof-

ing takes the shape of a sine wave. Verify that the sine curve

has equation and ﬁnd the width of a ﬂat

metal sheet that is needed to make a 28-inch panel. (Use your

calculator to evaluate the integral correct to four signiﬁcant

digits.)

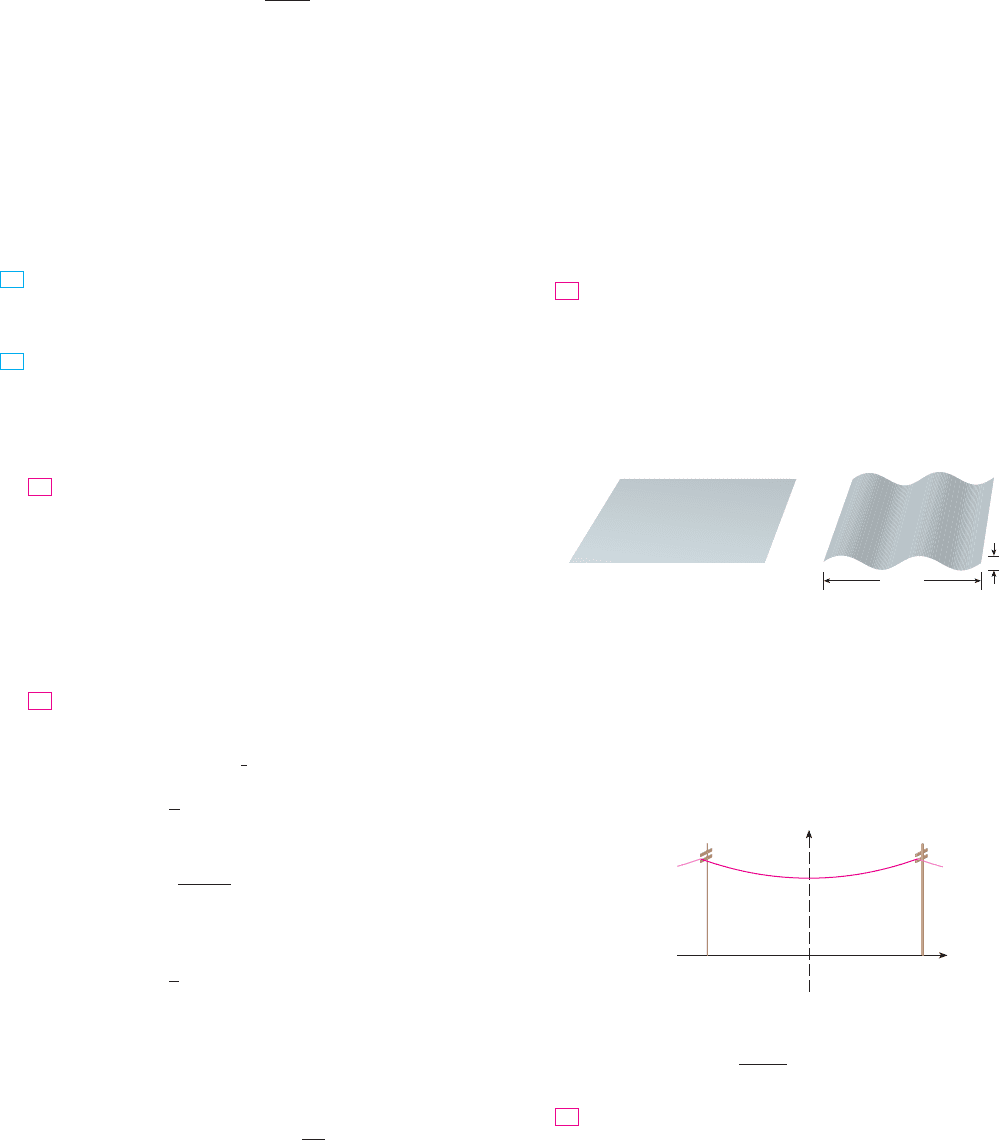
40. (a) The ﬁgure shows a telephone wire hanging between

two poles at and . It takes the shape of a

catenary with equation . Find the

length of the wire.

;

(b) Suppose two telephone poles are 50 ft apart and the

length of the wire between the poles is 51 ft. If the lowest

point of the wire must be 20 ft above the ground, how

high up on each pole should the wire be attached?

41. Find the length of the curve

;

The curves with equations , , , , . . . , are

called fat circles. Graph the curves with , , , , and

to see why. Set up an integral for the length of the fat

circle with . Without attempting to evaluate this inte-

gral, state the value of .lim

k

l

%

L

2k

n ! 2k

L

2k

10

864n ! 2

86n ! 4x

n

" y

n

! 1

42.

1 & x & 4y ! x

x

1

s

t

3

! 1 dt

y

0

x

_b b

y ! c " a cosh"x*a#

x ! bx ! !b

28 in

2 in

w

wy ! sin"

+

x*7#

39.

!

x

!

& 91.20

yx

y ! 211.49 ! 20.96 cosh 0.03291765x

;

27. (a) Graph the curve , .

(b) Compute the lengths of inscribed polygons with , ,

and sides. (Divide the interval into equal subintervals.)

Illustrate by sketching these polygons (as in Figure 6).

(c) Set up an integral for the length of the curve.

(d) Use your calculator to ﬁnd the length of the curve to four

decimal places. Compare with the approximations in

part (b).

;

28. Repeat Exercise 27 for the curve

29. Use either a computer algebra system or a table of integrals to

ﬁnd the exact length of the arc of the curve that lies

between the points and .

30. Use either a computer algebra system or a table of integrals to

ﬁnd the exact length of the arc of the curve that lies

between the points and . If your CAS has trouble

evaluating the integral, make a substitution that changes the

integral into one that the CAS can evaluate.

Sketch the curve with equation and use sym-

metry to ﬁnd its length.

32. (a) Sketch the curve .

(b) Use Formulas 3 and 4 to set up two integrals for the arc

length from to . Observe that one of these is

an improper integral and evaluate both of them.

(c) Find the length of the arc of this curve from

to .

Find the arc length function for the curve with

starting point .

;

34. (a) Graph the curve , .

(b) Find the arc length function for this curve with starting

point .

(c) Graph the arc length function.

35. Find the arc length function for the curve

with starting point .

36. A steady wind blows a kite due west. The kite’s height above

ground from horizontal position to is given

by

.

Find the distance traveled by the

kite.

37. A hawk ﬂying at at an altitude of 180 m accidentally

drops its prey. The parabolic trajectory of the falling prey is

described by the equation

until it hits the ground, where is its height above the ground

and is the horizontal distance traveled in meters. Calculatex

y

y ! 180 !

x

2

45

15 m*s

y ! 150 !

1

40

"x ! 50#

2

x ! 80 ftx ! 0

"0, 1#y ! sin

!1

x "

s

1 ! x

2

P

0

(

1,

7

12

)

x ' 0y !

1

3

x

3

" 1*"4x#

P

0

"1, 2#

y ! 2x

3*2

33.

"8, 4#

"!1, 1#

"1, 1#"0, 0#

y

3

! x

2

x

2*3

" y

2*3

! 1

31.

"1, 1#"0, 0#

y ! x

4*3

CAS

"2, ln 2#"1, 0#

y ! ln x

CAS

0 & x & 2

+

y ! x " sin x

4

2n ! 1

0 & x & 4

y ! x

s

3

4 ! x

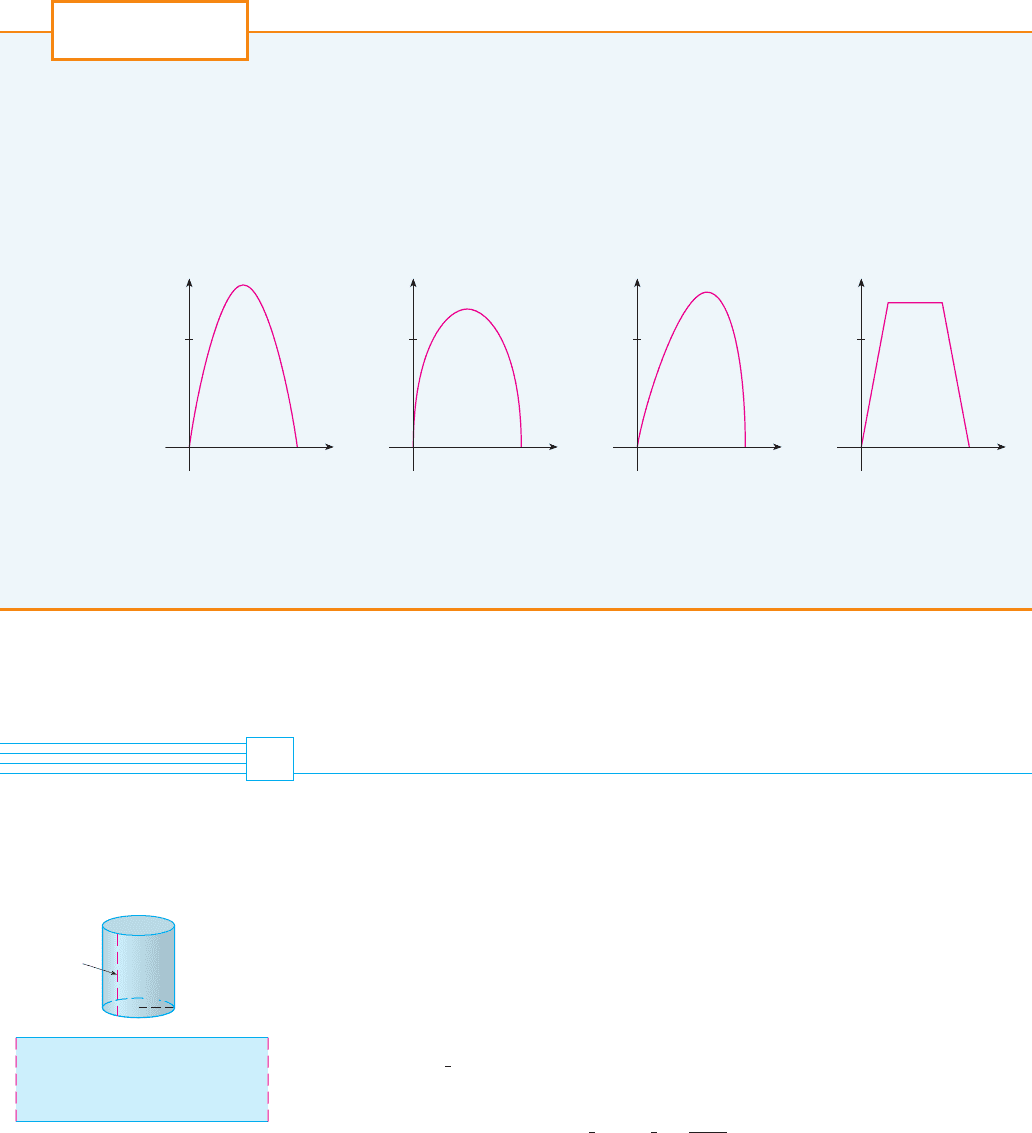
The curves shown are all examples of graphs of continuous functions that have the following

properties.

1.

2.

3.

The area under the graph of from 0 to 1 is equal to 1.

The lengths of these curves, however, are different.

Try to discover formulas for two functions that satisfy the given conditions 1, 2, and 3. (Your

graphs might be similar to the ones shown or could look quite different.) Then calculate the arc

length of each graph. The winning entry will be the one with the smallest arc length.

LÅ3.249

x

y

0 1

1

LÅ2.919

x

y

0 1

1

LÅ3.152

x

y

0 1

1

LÅ3.213

x

y

0 1

1

L

f

f "x# , 0 for 0 & x & 1

f "0# ! 0 and f "1# ! 0

f

ARC LENGTH CONTEST

D I S C O V E R Y

P R O J E C T

568

|| ||

CHAPTER 9 FURTHER APPLICATIONS OF INTEGRATION

AREA OF A SURFACE OF REVOLUTION

A surface of revolution is formed when a curve is rotated about a line. Such a surface is

the lateral boundary of a solid of revolution of the type discussed in Sections 6.2 and 6.3.

We want to deﬁne the area of a surface of revolution in such a way that it corresponds

to our intuition. If the surface area is , we can imagine that painting the surface would

require the same amount of paint as does a ﬂat region with area .

Let’s start with some simple surfaces. The lateral surface area of a circular cylinder with

radius and height is taken to be because we can imagine cutting the cylin-

der and unrolling it (as in Figure 1) to obtain a rectangle with dimensions and .

Likewise, we can take a circular cone with base radius and slant height , cut it along

the dashed line in Figure 2, and ﬂatten it to form a sector of a circle with radius and cen-

tral angle . We know that, in general, the area of a sector of a circle with radius

and angle is (see Exercise 35 in Section 8.3) and so in this case the area is

Therefore we deﬁne the lateral surface area of a cone to be .A !

+

rl

A !

1

2

l

2

)

!

1

2

l

2

(

2

+

r

l

)

!

+

rl

1

2

l

2

)

l

)

! 2

+

r*l

l

lr

h2

+

r

A ! 2

+

rhhr

A

9.2

h

2πr

F I G U R E 1

h

r

cut

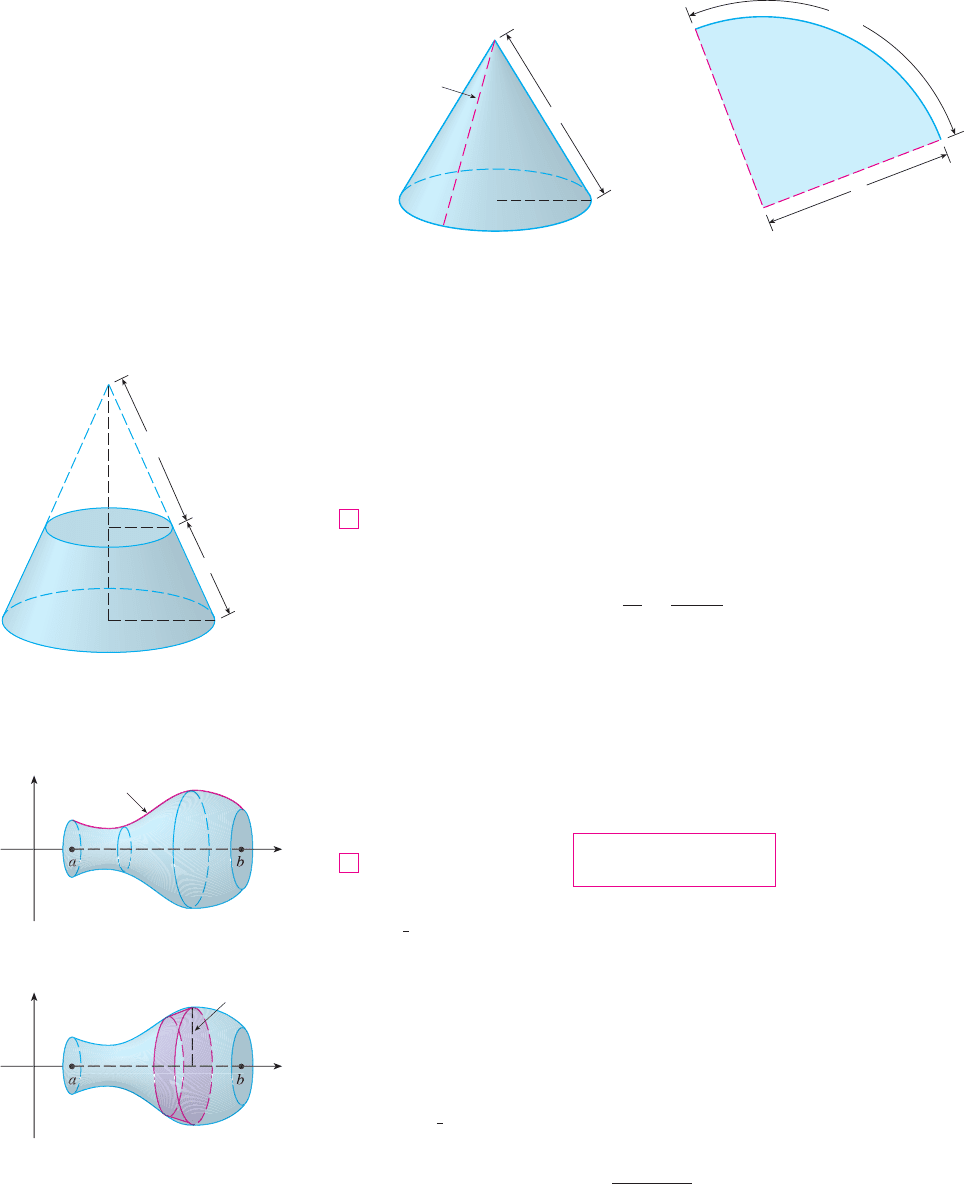
What about more complicated surfaces of revolution? If we follow the strategy we used

with arc length, we can approximate the original curve by a polygon. When this polygon

is rotated about an axis, it creates a simpler surface whose surface area approximates the

actual surface area. By taking a limit, we can determine the exact surface area.

The approximating surface, then, consists of a number of bands, each formed by rotat-

ing a line segment about an axis. To ﬁnd the surface area, each of these bands can be

considered a portion of a circular cone, as shown in Figure 3. The area of the band (or frus-

tum of a cone) with slant height and upper and lower radii and is found by sub-

tracting the areas of two cones:

From similar triangles we have

which gives

or

Putting this in Equation 1, we get

or

where is the average radius of the band.

Now we apply this formula to our strategy. Consider the surface shown in Figure 4,

which is obtained by rotating the curve , , about the -axis, where is

positive and has a continuous derivative. In order to deﬁne its surface area, we divide the

interval into n subintervals with endpoints and equal width , as we

did in determining arc length. If , then the point lies on the curve. The

part of the surface between and is approximated by taking the line segment

and rotating it about the -axis. The result is a band with slant height and aver-

age radius so, by Formula 2, its surface area is

2

+

y

i!1

" y

i

2

!

P

i!1

P

i

!

r !

1

2

"y

i!1

" y

i

#

l !

!

P

i!1

P

i

!

x

P

i!1

P

i

x

i

x

i!1

P

i

"x

i

, y

i

#y

i

! f "x

i

#

#xx

0

, x

1

, . . . , x

n

%a, b&

fxa & x & by ! f "x#

r !

1

2

"r

1

" r

2

#

A ! 2

+

rl

2

A !

+

"r

1

l " r

2

l#

"r

2

! r

1

#l

1

! r

1

lr

2

l

1

! r

1

l

1

" r

1

l

1

r

1

!

l

1

" l

r

2

A !

+

r

2

"l

1

" l# !

+

r

1

l

1

!

+

%"r

2

! r

1

#l

1

" r

2

l&

1

r

2

r

1

l

¨

2πr

F I G U R E 2

l

r

cut

SECTION 9.2 AREA OF A SURFACE OF REVOLUTION

|| ||

569

r¡

r™

l¡

l

F I G U R E 3

F I

G U

R E

4

0

x

y

y=ƒ

(

a) Sur

f

ace o

f

r

e

v

olution

P¸

P

i-1

P

i

P

n

y

i

0

x

y

(

b)

A

pproximatin

g

ban

d

As in the proof of Theorem 9.1.2, we have

where is some number in . When is small, we have and

also , since is continuous. Therefore

and so an approximation to what we think of as the area of the complete surface of revo-

lution is

This approximation appears to become better as and, recognizing (3) as a Riemann

sum for the function , we have

Therefore, in the case where is positive and has a continuous derivative, we deﬁne the

surface area of the surface obtained by rotating the curve , , about

the -axis as

With the Leibniz notation for derivatives, this formula becomes

If the curve is described as , , then the formula for surface area

becomes

and both Formulas 5 and 6 can be summarized symbolically, using the notation for arc

length given in Section 9.1, as

S !

y

2

!

y ds

7

S !

y

d

c

2

!

y

!

1 "

"

dx

dy

#

2

dy

6

c # y # dx ! t$y%

S !

y

b

a

2

!

y

!

1 "

"

dy

dx

#

2

dx

5

S !

y

b

a

2

!

f $x%

s

1 " & f $$x%'

2

dx

4

x

a # x # by ! f $x%

f

lim

n

l

%

(

n

i!1

2

!

f $x

i

*

%

s

1 " & f $$x

i

*

%'

2

&x !

y

b

a

2

!

f $x%

s

1 " & f $$x%'

2

dx

t$x% ! 2

!

f $x%

s

1 " & f $$x%'

2

n l %

(

n

i!1

2

!

f $x

i

*

%

s

1 " & f $$x

i

*

%'

2

&x

3

2

!

y

i'1

" y

i

2

)

P

i'1

P

i

)

* 2

!

f $x

i

*

%

s

1 " & f $$x

i

*

%'

2

&x

fy

i'1

! f $x

i'1

% * f $x

i

*

%

y

i

! f $x

i

% * f $x

i

*

%&x&x

i'1

, x

i

'x

i

*

)

P

i'1

P

i

)

!

s

1 " & f $$x

i

*

%'

2

&x

570

|| ||

CHAPTER 9 FURTHER APPLICATIONS OF INTEGRATION

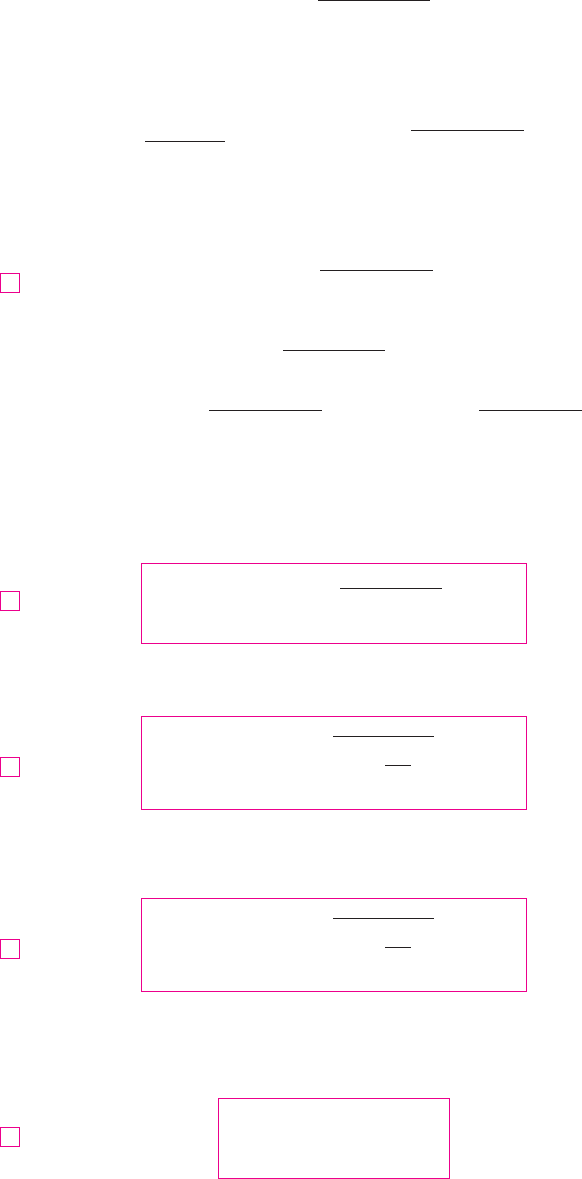
For rotation about the -axis, the surface area formula becomes

where, as before, we can use either

or

These formulas can be remembered by thinking of or as the circumference of a

circle traced out by the point on the curve as it is rotated about the -axis or -axis,

respectively (see Figure 5).

EXAMPLE 1 The curve , , is an arc of the circle .

Find the area of the surface obtained by rotating this arc about the -axis. (The surface is

a portion of a sphere of radius 2. See Figure 6.)

SOLUTION We have

and so, by Formula 5, the surface area is

M

! 4

!

y

1

'1

1 dx ! 4

!

$2% ! 8

!

! 2

!

y

1

'1

s

4 ' x

2

s

4 ' x

2

dx

! 2

!

y

1

'1

s

4 ' x

2

!

1 "

x

2

4 ' x

2

dx

S !

y

1

'1

2

!

y

!

1 "

"

dy

dx

#

2

dx

dy

dx

!

1

2

$4 ' x

2

%

'1+2

$'2x% !

'x

s

4 ' x

2

x

2

" y

2

! 4'1 # x # 1y !

s

4 ' x

2

V

F I G U R E 5 (a) Rotation about x-axis: S=j2πyds

(x,y)

y

circumference=2πy

x

0

y

(b) Rotation about y-axis: S=j2πxds

(x,y)

x

circumference=2πx

x

0

y

yx$x, y%

2

!

x2

!

y

ds !

!

1 "

"

dx

dy

#

2

dyds !

!

1 "

"

dy

dx

#

2

dx

S !

y

2

!

x ds

8

y

SECTION 9.2 AREA OF A SURFACE OF REVOLUTION

|| ||

571

N Figure 6 shows the portion of the sphere

whose surface area is computed in Example 1.

1

x

y

F I G U R E 6

Stewart J. Calculus

Подождите немного. Документ загружается.