Stewart J. College Algebra: Concepts and Contexts

Подождите немного. Документ загружается.

454 CHAPTER 5

■

Quadratic Functions and Models

example

Ticket Sales

A hockey team plays in an arena that has a seating capacity of 15,000 spectators.

With the ticket price set at $14, average attendance at recent games has been 9500.

A market survey indicates that for each dollar the ticket price is lowered, the aver-

age attendance increases by 1000.

(a) Find a function that models the revenue in terms of ticket price.

(b) At what ticket price is the revenue $100,000?

Solution

(a) In Example 5 of Section 5.3 we found the following function that models the

revenue R in terms of the ticket price x:

(b) We want to find the ticket price for which .

Model

Revenue is 100,000

Divide by 1000

Subtract 100

The expression on the left-hand side of this equation does not factor easily, so

we use the Quadratic Formula where a is , b is 23.5, and c is .

Using a calculator, we find

So the revenue is $100,000 when the ticket price is $17.92 or $5.58.

x L 17.92

orx L 5.58

- 23.5 ; 2152.25

- 2

x =

- 23.5 ; 21- 23.5 2

- 41- 121- 1002

21- 12

- 100-1

- 23.5x + 100 = 0

100 =-x

+ 23.5x

100,000 =-1000x

+ 23,500x

R1x 2=-1000x

+ 23,500x

R1x 2= 100,000

R1x 2=-1000x

+ 23,500x

150,000

_30,000

x=5.58 x=17.92

y=100,000

A graph of the revenue function R

shows that revenue is $100,000

when the ticket price is about $5.58

and $17.92.

(b) Suppose the lot has an area of 2900 square feet. Then

Model

Area of lot is 2900

Expand

Subtract 2900

Factor

Zero-Product Property

Since the width of a lot must be a positive number, we conclude that the width

is 50 feet. The length of the lot is feet.

■ NOW TRY EXERCISE 65 ■

w + 8 = 50 + 8 = 58

w = 50orw =-58

0 = 1w - 50 21w + 58 2

0 = w

+ 8w - 2900

2900 = w

+ 8w

2900 = w1w + 82

A1w 2= w1w + 82

SECTION 5.4

■

Quadratic Equations: Getting Information from a Model 455

Model

Revenue is 0

Divide by 1000

Factor

Zero-Product Property

According to this model, a ticket price of $23.50 is just too high; at that price,

no one attends the hockey game. (Of course the revenue is also zero if the

ticket price is zero.)

■ NOW TRY EXERCISE 67 ■

x = 0orx = 23.5

0 = x1- x + 23.52

0 =-x

+ 23.5x

0 =-1000x

+ 23,500x

R1x 2=-1000x

+ 23,500x

R1x 2= 0

150,000

_30,000

A graph of the revenue function R

shows that when the ticket

price x is 0 or $23.50 (the

x -intercepts of the graph).

R1x 2= 0

example

Model Rocket

A model rocket is shot straight upward with an initial speed of 800 ft/s, and the

height of the rocket is given by

where h is measured in feet and t in seconds.

(a) How many seconds does it take for the rocket to reach a height of 8000 feet?

(b) How long will it take the rocket to hit the ground?

Solution

(a) We want to find the time t such that .

Model

Height is 8000

Divide by 800

Subtract 10 and switch sides

The expression on the left-hand side does not factor easily, so we use the

Quadratic Formula where a is 0.02, b is , and c is 10.

Using a calculator, we find

So the rocket is at a height of 8000 feet after about 13.8 seconds and again

after 36.2 seconds.

(b) At ground level the height is 0, so we must solve the equation

Model

Height is 0

Factor

Zero-Product Property

t = 0ort = 50

0 = 16t1- t + 502

0 =-16t

+ 800t

h = 800t - 16t

t L 13.8ort L 36.2

1 ; 20.20

0.04

t =

1 ; 21- 12

- 410.02 21102

210.02 2

- 1

0.02t

- t + 10 = 0

10 = t - 0.02t

8000 = 800t - 16t

h = 800t - 16t

h = 8000

h = 800t - 16t

11,000

_1000

t=13.8 t=36.2

y=8000

A graph of the height function h

shows that the rocket reaches a

height of 8000 ft at times of about

13.8 s and 36.2 s.

11,000

_1000

A graph of the height function h

shows that when t is

about 0 or 50 seconds (the

t -intercepts of the graph).

h1t 2= 0

456 CHAPTER 5

■

Quadratic Functions and Models

Check your knowledge of factoring quadratic expressions by doing the following

problems. You can review this topic in

Algebra Toolkit B.2

on page T33.

1. Factor each expression by factoring out common factors.

(a) (b)

2. Factor the given expression using the Difference of Squares Formula.

(a) (b)

3. Factor the perfect square.

(a) (b)

4. Factor each expression by trial and error.

(a) (b)

- 7u - 32s

- s - 3

- t - 12x

+ 5x + 6

1u + 22

+ 101u + 22+ 259r

- 24r + 16

- 12t + 36x

+ 8x + 16

41w - 22

- 491u + 12

- 36

- 16x

- 36

12r + 3213r + 4 2- 513r + 4221x + 12

+ 1x + 12

- 6tx

+ x

According to this model, the rocket hits the ground after 50 seconds. (Of

course the rocket is also at ground level at time 0.)

■ NOW TRY EXERCISE 63 ■

Notice that the model in Example 8 is valid only for . For values of

t outside this interval the height h would be negative (that is, the rocket would be

traveling below ground level).

0 … t … 50

5.4 Exercises

CONCEPTS

Fundamentals

1. The Quadratic Formula gives us the solutions of the equation .

(a) State the Quadratic Formula:

______________.

(b) In the equation ,

_______, _______, and

_______. So the solution of the equation is ______.

2. To solve the quadratic equation , we can do the following.

(a) Factor the equation as , so the solutions are

_______

and _______.

(b) Use the Quadratic Formula to get

______________, so the solutions are

_______ and _______.

3. Let , and let .

(a) If , then the number of x-intercepts for the graph of f is

_______.

(b) If , then the number of x-intercepts for the graph of f is

_______.

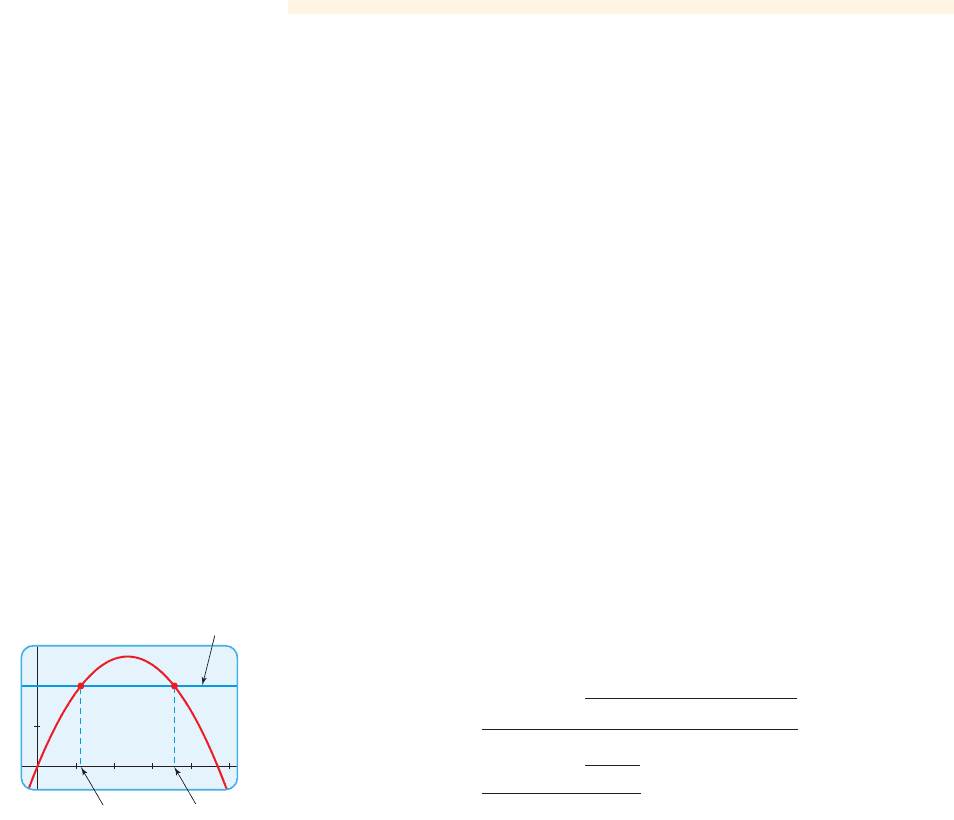
4. The graph of a quadratic function is shown at the top of the next page.

(a) The x-intercepts are

_______.

f 1x 2= ax

+ bx + c

D 6 0

D = 0

D 7 0

D = b

- 4acf 1x 2= ax

+ bx + c

x =

1x - ____2

1x + ____2= 0

- 4x - 5 = 0

x =c =

b =a =

- x - 4 = 0

x =

+ bx + c = 0

SECTION 5.4

■

Quadratic Equations: Getting Information from a Model 457

(b) The discriminant of the equation is _______ (positive, 0, or

negative).

_______.

Think About It

5. Consider the quadratic function .

(a) The graph is a parabola that opens

_______.

(b) The x-intercepts are

_______ and _______.

x-coordinate of the vertex is

_____________.

6. Consider the quadratic function .

(a) The graph is a parabola that opens

_____________.

(b) The x-intercepts are

_______ and _______.

x-coordinate of the vertex is

_______.

(d) Using the formula we found in part (c), we find that the x-coordinate of the vertex

of is

_______.

7–16

■ Solve the equation by factoring.

7. 8.

9. 10.

11. 12.

13. 14.

15. 16.

17–20

■ A graph of a quadratic function f is given.

(a) Find the x-intercepts.

(b) Find an equation that represents the function f (as in Example 3).

17. 18.

+ 1 = 4x6x

+ 5x = 4

= 4w + 32y

+ 7y + 3 = 0

- 4x - 15 = 03s

- 5s - 2 = 0

+ 8t + 12 = 0t

- 7t + 12 = 0

+ 3x = 4x

+ x = 12

y = 1x - 3 21x - 5 2

y = 1x - m 21x - n 2

y = 1x - 2 21x - 4 2

+ bx + c = 0

SKILLS

135

3_1

19. 20.

1_3

1_2

Graph for Exercise 4

458 CHAPTER 5

■

Quadratic Functions and Models

21–26

■ Solve the equation by both factoring and using the Quadratic Formula.

21. 22.

23. 24.

25. 26.

27–38

■ Find all real solutions of the equation.

27. 28.

29. 30.

31. 32.

33. 34.

35. 36.

37. 38.

39–42

■ Solve the quadratic equation algebraically and graphically, correct to three

decimal places.

39. 40.

41. 42.

43–48

■ A quadratic function is given.

(a) Find the discriminant of the equation . How many real solutions

does this equation have?

(b) Use the answer to part (a) to determine the number of x-intercepts for the graph of

the function , and then graph the function to confirm your

answer.

43. 44.

45. 46.

47. 48.

49–52

■ A graph of a quadratic function is shown.

(a) Find the x-intercept(s), if there are any.

(b) Is the discriminant positive, negative, or 0?

(d) Find an equation that represents the function f.

49. 50.

+ bx + c = 0

D = b

- 4ac

f 1x 2= ax

+ bx + c

f 1x 2= 9x

- 4x +

f 1x 2= 32x

+ 40x + 13

f 1x 2= 0.1x

- 0.38x + 0.361f 1x 2= x

+ 2.20x + 1.21

f 1x 2= x

- 6x + 9f 1x2= x

- 6x + 1

f 1x 2= ax

+ bx + c

+ bx + c = 0

f 1x 2= ax

+ bx + c

- 1.800x + 0.810 = 0x

- 2.450x + 1.501 = 0

- 2.450x + 1.500 = 0x

- 0.011x - 0.064 = 0

25y

+ 70y + 49 = 010y

- 16y + 5 = 0

- 7x + 5 = 0x

- 15x + 1 = 0

2 + 2z + 3z

= 0w

= 31w - 12

- 6s + 1 = 0s

s +

= 0

- 6y - 9 = 0y

+ 12y - 27 = 0

- 8t + 4 = 0t

+ 3t + 1 = 0

+ 7x + 4 = 02x

+ x - 3 = 0

+ 30x + 200 = 0x

- 7x + 10 = 0

+ 5x - 6 = 0x

- 2x - 15 = 0

1_1

(_1, 1)

SECTION 5.4

■

Quadratic Equations: Getting Information from a Model 459

51. 52.

53–60

■ A quadratic function is given.

(a) Find the x-intercepts of the graph of f.

(b) Sketch the graph of f and label the x- and y-intercepts and the vertex.

53. 54.

55. 56.

57. 58.

59. 60.

61. Height of a Ball If a ball is thrown directly upward with a velocity of 12 m/s, its

height (in meters) after t seconds is modeled by .

(a) When does the ball reach a height of 5 meters?

(b) Does the ball reach a height of 8 meters?

(d) Identify the points on the graph that correspond to your solutions to parts (a)–(c).

f 1t 2= 12t - 4.9t

f 1x 2= 2x

+ 8x + 11f 1x 2= 3x

- 12x + 13

f 1x 2= 1 - x - x

f 1x 2=-x

- 3x + 3

f 1x 2= 5x

+ 30x + 4f 1x 2= 3x

- 6x + 1

f 1x 2= x

- 8x + 8f 1x2= x

+ 2x - 1

f 1x 2= ax

+ bx + c

CONTEXTS

2015105

62. Path of a Ball A ball is thrown across a playing field from a height of 5 ft above the

ground at an angle of to the horizontal at a speed of 20 ft/s. It can be deduced from

physical principles that the path of the ball is modeled by the function

where x is the distance in feet that the ball has traveled horizontally.

(a) At what horizontal distance x is the ball 7 ft high?

(b) Does the ball reach a height of 10 ft?

(d) Identify the points on the graph in the margin that correspond to your solutions to

parts (a)–(c).

f 1x2=-

120 2

+ x + 5

45°

460 CHAPTER 5

■

Quadratic Functions and Models

63. Height of a Rocket A model rocket shot straight upward with an initial velocity of

m/s will reach a height of h meters in t seconds, where the height h is modeled by

(a) When does the rocket reach a height of 20 m?

(b) When does the rocket reach the highest point of its path?

(d) Graph the function h and identify the points on the graph that correspond to your

solutions to parts (a)–(c).

64. Height of a Ball A ball is thrown straight upward with an initial velocity of ft/s. It

will reach a height of h feet in t seconds, where the height h is modeled by the function

(a) Show that the ball reaches its maximum height when .

(b) Show that the ball reaches a maximum height of .

65. Dimensions of a Lot A rectangular building lot is 40 ft longer than it is wide. (See

the figure to the left.)

(a) Find a function A that models the area of the lot.

(b) If the lot has an area of , then what are the dimensions of the lot?

66. Width of a Lawn A factory is to be built on a lot measuring 180 ft by 240 ft. A local

building code specifies that a lawn of uniform width and equal in area to the factory

must surround the factory. Let w be the width of the lawn, as shown in the figure.

(a) Find a function A that models the area of the factory in terms of w.

(b) What must the width of the lawn be, and what are the dimensions of the factory?

11,700 ft

√

>64

t = √

>32

h1t 2=-16t

+ √

√

h1t 2=-4.9t

+ 25t

√

67. Stadium Revenue A baseball team plays in a stadium that holds 55,000 spectators.

With the ticket price at $10, the average attendance at recent games has been 27,000. A

market survey indicates that for every dollar the ticket price is lowered, attendance

increases by 3000. (See Exercise 33 in Section 5.3.)

(a) Find a function that models the revenue in terms of ticket price.

(b) What ticket price is so high that no revenue is generated?

they charge to meet this goal?

68. Bird Feeders A community bird-watching society makes and sells simple bird

feeders to raise money for its conservation activities. The materials for each feeder cost

$6, and the society sells an average of 20 feeders per week at a price of $10 each. The

society has been considering raising the price, so it conducts a survey and finds that for

every dollar increase, it loses two sales per week. (See Exercise 34 in Section 5.3.)

(a) Find a function P that models weekly profit in terms of price per feeder.

(b) What ticket price is so high that no profit is generated?

nature center. What price should the society charge per feeder to meet this goal?

x+40

SECTION 5.5

■

Fitting Quadratic Curves to Data 461

5.5 Fitting Quadratic Curves to Data

■

Modeling Data with Quadratic Functions

IN THIS SECTION… we learn how to model data using the quadratic function of

best fit.

The importance of proper tire inflation cannot be overestimated. A car’s tendency to

skid as well as the tire’s potential to overheat and explode are some of the safety fac-

tors associated with tire inflation. Proper tire inflation also affects a car’s ability to

handle tight curves, which is the reason race car drivers pay special attention to tire

pressure. Today, many passenger cars have a Tire Pressure Monitoring (TPM) sys-

tem, which continually monitors tire pressure and warns the driver of unsafe pres-

sure levels. The first passenger vehicle to adopt a TPM system was the Porsche 959

in 1986.

Gas mileage and tire wear are also affected by tire inflation. So what exactly is

proper pressure? And how can we determine the proper tire pressure? To find the tire

pressure that maximizes tire life, researchers perform experiments in which tires un-

der different inflation pressures are rolled along special surfaces. The data exhibit an

increasing and then decreasing pattern, so a quadratic function is appropriate for

modeling the data.

■

The data give tire life for different inflation pressures.

■

The model is a quadratic function that best fits the data.

■

Our goal is to use the model to predict the inflation pressure that gives the

longest tire life.

We’ll see in this section how this modeling technique works, and we’ll solve the tire

inflation problem in Example 2.

■ Modeling Data with Quadratic Functions

We have learned how to fit a line to data (Section 2.5). The line models the increas-

ing or decreasing trend of the data. If the data exhibit more variability, such as an in-

crease followed by a decrease, then to model the data we need a curve rather than a

line. Figure 1 shows a scatter plot with two possible models that appear to fit the data.

Which model appears to fit the data better?

543

(a) Linear model

54321

(b) Quadratic model

figure 1

Proper tire inflation is

particularly important in driving

on roads with tight curves, such

as this section of Pacific Coast

Highway in California.

462 CHAPTER 5

■

Quadratic Functions and Models

We can use a graphing calculator to find a quadratic model that fits any given

set of data.

example

Finding the Quadratic Curve of Best Fit

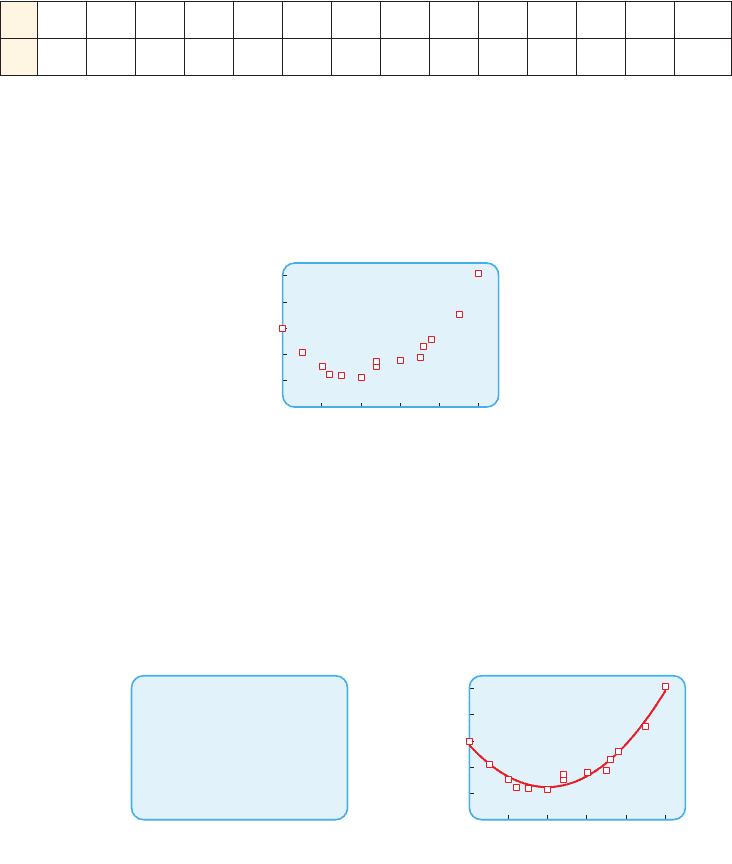
(a) Make a scatter plot of the data in Table 1. Is it appropriate to model the data

by a quadratic function?

(b) Use a graphing calculator to find the quadratic model that best fits the data.

Draw a graph of the model.

x 0.0 0.5 1.0 1.2 1.5 2.0 2.4 2.4 3.0 3.5 3.6 3.8 4.5 5.0

y 6.0 4.2 3.1 2.5 2.4 2.3 3.5 3.1 3.6 3.8 4.6 5.2 7.1 10.2

table 1

5.5

figure 2 Scatter plot of data

Solution

(a) A scatter plot is shown in Figure 2. From the data we see that the y-values

appear to decrease and then increase, so a quadratic model is appropriate.

5.5

(b) Graph of quadratic model(a) Result of QuadReg command

QuadReg

y=ax

+bx+c

a=.80589

b=-3.1959

c=5.6699

figure 3

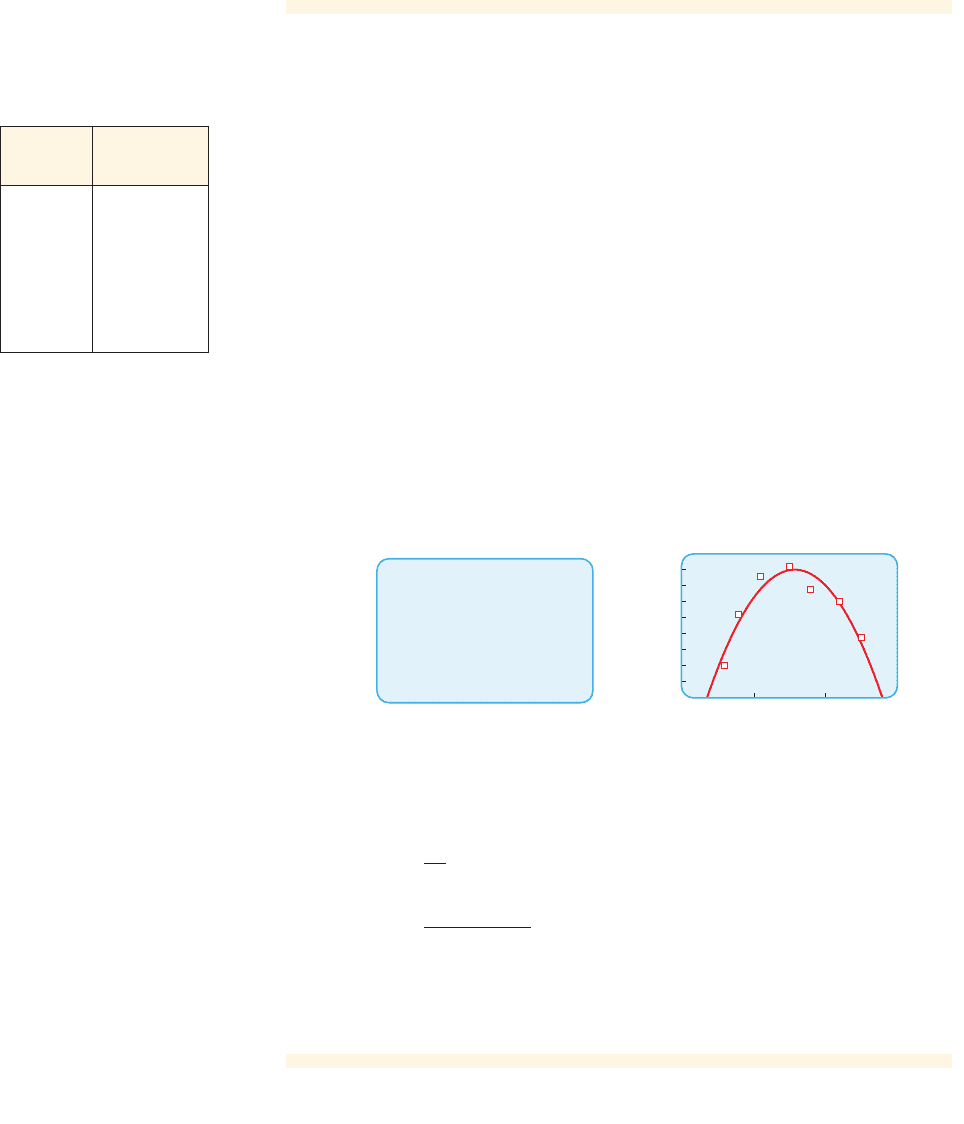
(b) Using the QuadReg command on a graphing calculator, we obtain the result

in Figure 3(a). Thus, the quadratic function of best fit is

A graph of this function together with the scatter plot is shown in Figure 3(b).

y = 0.80589x

- 3.1959x + 5.6699

SECTION 5.5

■

Fitting Quadratic Curves to Data 463

Model

Replace x by 6

Calculator

■ NOW TRY EXERCISE 5 ■

= 15.507

= 0.80589162

- 3.195916 2+ 5.6699

y = 0.80589x

- 3.1959x + 5.6699

example

Proper Tire Inflation

Car tires need to be inflated properly. Overinflation or underinflation can cause pre-

mature tread wear. The data in Table 2 show tire life (in thousands of miles) for dif-

ferent inflation pressures for a certain type of tire.

(a) Find the quadratic function that best fits the data.

(b) Draw a graph of the quadratic model from part (a) together with a scatter plot

of the data.

longest tire life.

Solution

(a) Using the QuadReg command on a graphing calculator, we obtain the

quadratic function that best fits the data.

(See Figure 4(a).)

(b) The graph and scatter plot are shown in Figure 4(b).

y =-0.27543x

+ 19.7485x - 273.55

(

)(

)

QuadReg

y=ax

+bx+c

a=-.2754277382

b=19.7485275

c=-273.552

figure 4

table 2

Pressure

21lb

Tire life

1mi ⴛ 1000 2

26 50

28 66

31 78

35 81

38 74

42 70

45 59

from Section 5.3, we see that the maximum value occurs at

Formula

Replace b by 19.7485 and a by

Calculator

So the inflation pressure that gives the maximum tire life is about 36 lb/in

■ NOW TRY EXERCISE 9 ■

= 35.8503

- 0.27543 =-

19.7485

21- 0.275432

x =-