Суляндзига Е.П., Ушакова Г.А. Тесты по математике: Предел, производная, элементы алгебры и геометрии
Подождите немного. Документ загружается.


33
Ответ
:
( )
6
5
'
8
8 3 .
5
y x
-
= - +
Пример 25
. Найти производную функции
( )
3
1
4 5
y
cos x
=
+
.
Решение
Преобразуем заданную функцию
( )
( )
( )
( )
( )
3
3 3
1 1
4 5
4 5
4 5
y cos x
cos x
cos x
-
= = = +
+
+
.
Сначала надо дифференцировать степенную функцию
( )
3
...
-
, затем
тригонометрическую
(
)
...
cos
, и только потом линейную
4 5
x
+
. Согласно
правилу дифференцирования сложной функции будем иметь
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
'
3 4
'
4 4
4 5 3 4 5 4 5 4
4 5 4 5
12 12 .
4 5
4 5
y cos x cos x sin x
sin x sin x
cos x
cos x
- -
ж ц
ч
з
= + = - + Ч- + Ч =
ч
чз
и ш
+ +
= =
+
+
Ответ
:
( )
6
5
'
8
8 3 .
5
y x
-
= - +
Пример 26
. Найти производную функции
( )
3
1
4 5
y
cos x
=
+
.
Решение
Преобразуем функцию
( )
( )
( )
( )
( )
3
3 3
1 1
4 5
4 5
4 5
y cos x
cos x
cos x
-
= = = +
+
+
.
Сначала дифференцируем степенную функцию
( )
3
...
-
, затем тригоно-
метрическую
(
)
...
cos
, и только потом линейную
4 5
x
+
. Согласно правилу
дифференцирования сложной функции получим
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
'
3 4
'
'
4 4 4
4 5 3 4 5 4 5 4
4 5 4 5 4 5
12 12 . : 12 .
4 5 4 5
4 5
y cos x cos x sin x
sin x sin x sin x
Ответ y
cos x cos x
cos x
- -
ж ц
ч
з
= + = - + Ч- + Ч =
ч
чз
и ш
+ + +
= = =
+ +
+
34
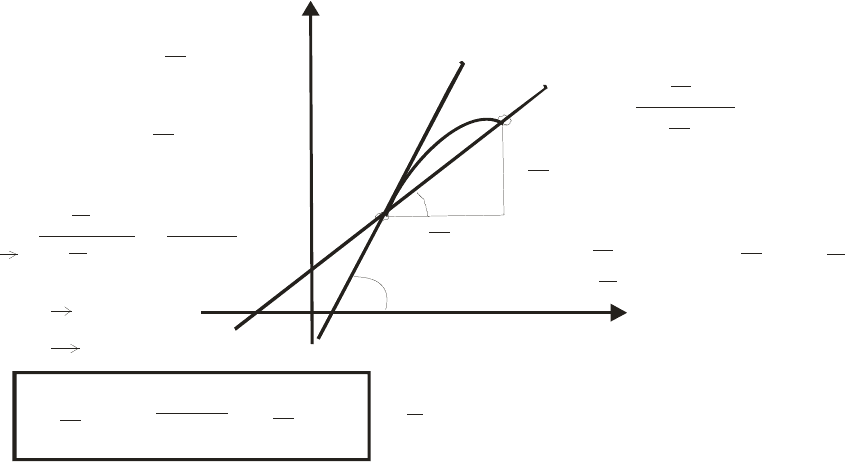
Уравнение касательной
Рассмотрим функцию
(
)
y f x
=
.
Точка
(
)
0 0; 0
M x y
принадлежит графику
этой функции. Надо написать уравнение касательной к графику этой
функции, проходящей через точку
(
)
0 0; 0
M x y
.
Воспользуемся геометрическим смыслом производной функции в точ-
ке – это тангенс угла наклона касательной с положительным направлени-
ем оси
Ox
. На рис.
1 выполнены построение касательной и получение ис-
комого уравнения.
M
M
M
0
0
00
0
0
0
0
0
0
M
x
x
x
x
x
x
x
x
x
x
x
x
x
x
α
α
α
y
y
y
y
y
y
dy
y
y
y
y
y
=
=
tg
tg
tg
=
k
k
(
(
(
)
)
)
;
;
заданная
точка
точка
текущая
β
lim
0
0
=
dx
= tg
β
tg
β
0
α
(x
0
)
y
y
при x
0
0
0
0
(x
(x
x
)=
dy
)
dx
уравнение касательной
уравнение секущей
Рис.1 Уравнение касательной к графику функции
Дифференциал функции
Это очень важное понятие. Но так складываются обстоятельства, что
мало кто из учащихся даст определение дифференциала функции: диф-
ференциал функции – это главная линейная часть приращения функции.
Дифференциал функции обозначаем
dy
и находим как
'
dy y dx
=
. А ведь для
инженера это первое правило приближенного вычисления некоторого зна-
чения:
( ) ( ) ( )
' '
0 0 0
.
y dy y y dx f x x f x f x x
∆ ≈ → ∆ ≈ → + ∆ ≈ + ∆
Напомним, что
для аргумента
,
x dx
∆ =
для функции
y dy
∆ ≈
. Можно сказать, что использо-
вание калькулятора, и тем более персональных компьютеров, сделало не-
надобной эту работу.

35
Область, где не обойтись без знания дифференциала функции остает-
ся интегрирование. Если усвоить свойство дифференциала функции та-
кое, как
инвариантность формы
, т.е.
неизменность формы
, то в про-
стейших случаях в неопределенном и определенном интегралах можно
обойтись без замены переменной. Это свойство можно назвать иначе:
подведением множителя, стоящего перед знаком дифференциала, за знак
дифференциала.
Пример 27.
Преобразовать дифференциалы десяти заданных функ-
ции, используя свойство
инвариантности формы
дифференциала.
1)
,
xdx
2)
(
)
3 2 ,
x dx
+
3)
2
,
x dx
4)
1
,
2
dx
x
+
5)
3
,
2 1
dx
x
−
6)
,
sinxdx
7)
,
cos3xdx
8)
(
)
2 ,
cos 3x dx
+
9)
2
1
,
1 4
dx
x
+
10)
2
1
.
1 9
dx
x−
Решение
Будем использовать свойства линейности дифференциала, где
,
k C
−
произвольные постоянные:
( ) ( )
1
, ,
dx d x C dx d kx
k
= ± =
( )
1
.
dx d kx C
k
= ±
Следите за решениями и попытайтесь объяснить каждый шаг.
1)
2
1
,
2
xdx dx
=
2)
( )
(
)
2
1
3 2 3 2 ,
2
x dx d x x
+ = +
3)
2 3
1
,
3
x dx dx
=
4)
( )
1
2 ,
2
dx dln x
x
= +
+
5)
( )
3 3
2 1 ,
2 1 2
dx ln x
x
= −
−
6)
cos ,
sinxdx d x
= −
7)
1
,
3
cos3xdx dsin3x
=
8)
( ) ( )
1
2 2 ,
3
cos 3x dx dsin 3x+ = +
9)
( ) ( )
( ) ( )
2 2 2
1 1 1 1 1
2 2 ,
2 2
1 4
1 2 1 2
dx dx d x darctg x
x
x x
= = =
+
+ +
10)
( ) ( )
( ) ( )
2 2 2
1 1 1 1 1
3 3 .
3 3
1 9
1 3 1 3
dx dx d x darcsin x
x
x x
= = =
−
− −

36
Правило Лопиталя
8
Правило Лопиталя – это правило раскрытия неопределенностей вида
0
0
и
∞
∞
. Суть его в том, что предел отношения функций сводится к пределу
отношения производных рассматриваемых функций. Если в пределе от-
ношения производных вновь присутствует неопределенность одного из
указанного вида, то процесс продолжается, в качестве же исходных функ-
ций выступают производные. Это правило было найдено И. Бернулли и
сообщено им Г. Лопиталю, который опубликовал его в 1696 г.
Рассмотрим отношение двух функций
(
)
f x
и
(
)
g x
:
(
)
( )
f x
g x
.
Пусть функции
(
)
f x
и
(
)
g x
дифференцируемы в некоторой окрест-
ности точки
0
x
, кроме, может быть, самой этой точки. Полагаем, что
( )
'
0
g x
№
для всех значений аргумента из этой окрестности. Тогда, если
(
)
(
)
0 0
lim lim 0
x x x x
f x g x
® ®
= =
( в отношении
(
)
( )
f x
g x
имеем неопределенность ви-
да
0
0
) и существует
( )
( )
0
'
'
lim
x x
f x
g x
→
, то существует и
(
)
( )
0
lim
x x
f x
g x
→
, при этом
( )
( )
( )
( )
0 0
'
'
0
lim lim
0
x x x x
f x f x
g x
g x
→ →
= =
.
П р и м е ч а н и е . Если
( )
( )
( )
( )
0 0
'
'
0 0
lim lim
0 0
x x x x
f x f x
g x
g x
→ →
= = =
, то приме-
нение правила Лопиталя надо продолжить:
( )
( )
( )
( )
( )
( )
0 0 0
'
'
"
0 0
lim lim lim
0 0 "
x x x x x x
f x f x f x
g x g x
g x
→ → →
= = = =
.
Пусть функции
(
)
f x
и
(
)
g x
дифференцируемы в некоторой окрест-
ности точки
0
x
, кроме, может быть, самой этой точки. Полагаем, что
( )
'
0
g x
№
для всех значений аргумента из этой окрестности. Тогда, если
8
Гийом Франсуа Антуан де Лопиталь (Guillaume Francois Antoine de Lhopital) (1661−1704) − фран-
цузский математик. Автор первого печатного учебника по дифференциальному исчислению (1696 г.), в
основу которого были положены лекции И. Бернулли.

37
(
)
(
)
0 0
lim lim
x x x x
f x g x
® ®
= = Ґ
(в отношении
(
)
( )
f x
g x
имеем неопределенность
вида
∞
∞
) и существует
( )
( )
0
'
'
lim
x x
f x
g x
→
, то существует и
(
)
( )
0
lim
x x
f x
g x
→
, причем
( )
( )
( )
( )
0 0
'
'
lim lim
x x x x
f x f x
g x
g x
→ →
∞
= =
∞
.
П р и м е ч а н и е . Если
( )
( )
( )
( )
0 0
'
'
lim lim
x x x x
f x f x
g x
g x
→ →
∞ ∞
= = =
∞ ∞
, то приме-
нение правила Лопиталя надо продолжить:
( )
( )
( )
( )
( )
( )
0 0 0
'
'
"
lim lim lim
"
x x x x x x
f x f x f x
g x g x
g x
→ → →
∞ ∞
= = = =
∞ ∞
.
Применение правила Лопиталя
.
Пример 28
. Найти
0
1
lim
x
x
e
sinx
→
−
.
Решение
0 0
1 0 1
lim lim 1.
0 1
x x
x x
e e
sinx cosx
→ →
−
= = = =
Ответ
:
0
1
lim 1.
x
x
e
sinx
→
−
=
Пример 28
. Найти
3
lim
2
x
sin x
sin x
π
→
.
Решение
3 0 3 3 3 1 3
lim lim .
2 0 2 2 2 1 2
x x
sin x cos x
sin x cos x
π π
→ →
−
= = = ⋅ = −
Ответ
:
3 3
lim
2 2.
x
sin x
sin x
π
→
= −

38
Пример 30
. Найти
2
lim
2
x
x tgx
π
π
→
− ⋅
.
Решение
2
2
2 2 2 2
0 1
2
lim lim lim lim 1.
1
2 0
x x x x
x
x tgx sin x
ctgx
sin x
π π π π
π
π
→ → → →
−
−
− ⋅ = = = = =
−
Ответ
:
2
lim 1.
2
x
x tgx
π
π
→
− ⋅ =
Рассмотрим три функции: натуральный логарифм
lnx
, степенную
n
x
и показательную
.
x
a
Поведение каждой из них при условии
x
→ ∞
из-
вестно. Они неограниченно возрастают:
lim ; lim ; lim .
n x
x x x
lnx x a
→∞ →∞ →∞
= ∞ = ∞ = ∞
Но какая из них растет быстрее по сравнению с другой, а какая мед-
леннее? Чтобы ответить на этот вопрос, надо изучить поведение отноше-
ния двух исследуемых функций при условии
x
→ ∞
. А поскольку отноше-
ние этих двух функций при
x
→ ∞
дает неопределенность вида
∞
∞
, то
здесь уместно использовать правило Лопиталя.
Пример 31
. Найти
3
lim
x
ln x
x
→∞
.
Решение
1
3
3 1 1
3
lim lim lim 0.
1
x x x
ln x
x
x x
→∞ →∞ →∞
⋅
= = = =
∞
Ответ
:
3
lim 0
x
ln x
x
→∞
=
.
Вывод
: функция
3
y ln x
=
(натуральный логарифм) при
x
→ ∞
рас-
тет медленнее, чем линейная функция
.
y x
=
Изобразите графики этих
функций на плоскости
.
xOy
39
Пример 32
. Найти
3
2
lim
x
ln x
x
→∞
.
Решение
3 2 3
1
2
2 1 1 1
2
lim lim lim 0.
3
3
x x x
ln x
x
x x x
→∞ →∞ →∞
⋅
= = = =
∞
Ответ
:
3
2
lim 0.
x
ln x
x
→∞
=
Вывод
. Логарифмическая функция
2
y ln x
=
(натуральный лога-
рифм) при
x
→ ∞
растет медленнее, чем степенная функция
3
.
y x
=
Изо-
бразите графики этих функций на плоскости
.
xOy
Пример 33
. Найти
lim
2
x
x
x
→∞
.
Решение
1 1
lim lim 0.
2 2 2
x x
x x
x
ln
→∞ →∞
= = =
∞
Ответ
:
lim 0.
2
x
x
x
→∞
=
Вывод
. Линейная функция
y x
=
при
x
→ ∞
растет медленнее, чем
показательная функция
2 .
x
y =
Изобразите графики этих функций на плос-
кости
.
xOy
Пример 34
. Найти
3
lim
2
x
x
x
→∞
.
Решение
( )
( )
3 2
2
3
3 3 2
lim lim lim
2 2 2
2 2
6 6
lim 0.
2 2
x x
x
x x x
x
x
x x x
ln
ln
ln
→∞ →∞ →∞
→∞
∞ ∞ ⋅ ∞
= = = = = =
∞ ∞ ∞
= = =
∞
Ответ
:
3
lim 0.
2
x
x
x
→∞
=

40
Вывод
. Степенная функция
3
y x
=
при
x
→ ∞
растет медленнее,
чем показательная функция
2 .
x
y =
Изобразите графики этих функций на
плоскости
.
xOy
Возникает вопрос
. Справедливы ли следующие утверждения?
1. Логарифмическая функция при
x
→ ∞
растет медленнее, чем сте-
пенная функция;
2. Степенная функция при
x
→ ∞
растет медленнее, чем показатель-
ная функция.
3. Логарифмическая функция при
x
→ ∞
растет медленнее, чем пока-
зательная функция.
Внимание
. Речь идет о логарифмической функции с любым основа-
нием, а не только о натуральном логарифме.
3. ФУНКЦИЯ. ОБЛАСТЬ ОПРЕДЕЛЕНИЯ
Предположим, даны две переменные величины
x
и
y
. Переменная
x
независимая, ее называют
аргументом
. Переменная
y
зависит от
x
,
закон
f
описывает эту зависимость, например,
2
y x
=
. Здесь закон
f
есть
возведение независимой переменной
x
в квадрат. Зависимость
y
от
x
за-
писывается
(
)
y f x
=
, и
y
называется
функцией
от
x
.
Множество значений переменной
x
, при которых функция
(
)
y f x
=
имеет смысл, называется
областью определения
функции
либо
обла-
стью допустимых значений
функции.
Пример 35
. Найти область определения функции
3 5
2
x
y
x
+
=
−
.
Решение
Заданная функция
3 5
2
x
y
x
+
=
−
– рациональная функция, т.е. отношение
двух линейных выражений
3 5
x
+
и
2
x
−
. В знаменателе находится ли-
нейное выражение
2
x
−
. Для того, чтобы функция
3 5
2
x
x
+
−
имела смысл,
необходимо и достаточно, чтобы знаменатель этой дроби был отличен от
нуля:
2 0
x
− ≠
, т.е.
2
x
≠
. Отсюда вывод: областью определения заданной
функции
3 5
2
x
y
x
+
=
−
является вся вещественная ось за исключением
2
x
=
.
Этот факт записывается:
(
)
(
)
;2 2; .
x
∈ −∞ +∞
U
Ответ
:
(
)
(
)
;2 2; .
x
∈ −∞ +∞
U
41
Пример 36.
Найти область определения функции
(
)
3
y ln x
= +
.
Решение
Функция
y
−
натуральный логарифм, т.е. логарифмическая функция,
основание которой есть иррациональное число е
≈
2,718:
(
)
(
)
3 3
e
y log x ln x
= + = +
. Известно, что аргумент логарифмической функции
должен быть положительным. В нашем случае аргументом функции явля-
ется выражение
3
x
+
. Следовательно, область определения функции
(
)
3
y ln x
= +
записывается в виде неравенства
3 0
x
+ >
, или
3
x
> −
, что рав-
носильно выражению
(
)
3; .
x
∈ − ∞
Ответ
:
(
)
3; .
x
∈ − ∞
4.
НЕПРЕРЫВНОСТЬ ФУНКЦИИ
Говоря о непрерывности функции
(
)
y f x
=
в точке
x a
=
, надо заметить,
что существует несколько определений непрерывности.
Первое определение
Функция
(
)
y f x
=
непрерывна в точке
x a
=
, если бесконечно малому
приращению аргумента
x
∆
соответствует бесконечно малое приращения
функции
y
∆
.
Второе определение
Функция
(
)
y f x
=
непрерывна в точке
x a
=
, если выполнены требова-
ния:
1. Функция
(
)
y f x
=
определена в точке
x a
=
, т.е. существует
(
)
f a
;
2. Существует предел функции
(
)
y f x
=
при
x
, стремящемся к
a
сле-
ва, т.е. существует
(
)
0
lim
x a
f x
→ −
.
Существует предел функции
(
)
y f x
=
при
x
, стремящемся к
a
справа, т.е.
существует
(
)
+0
lim
x a
f x
→
.
3. Предел функции слева равен пределу функции справа, т.е.
(
)
(
)
0 +0
lim lim
x a x a
f x f x
→ − →
=
, и оба этих предела равны значению функции в
точке
x a
=
, т.е.
(
)
(
)
(
)
0 +0
lim lim
x a x a
f x f x f a
→ − →
= =
.
Надо заметить, что второе определение есть руководство к реше-
нию задачи на установление непрерывности функции в точке.
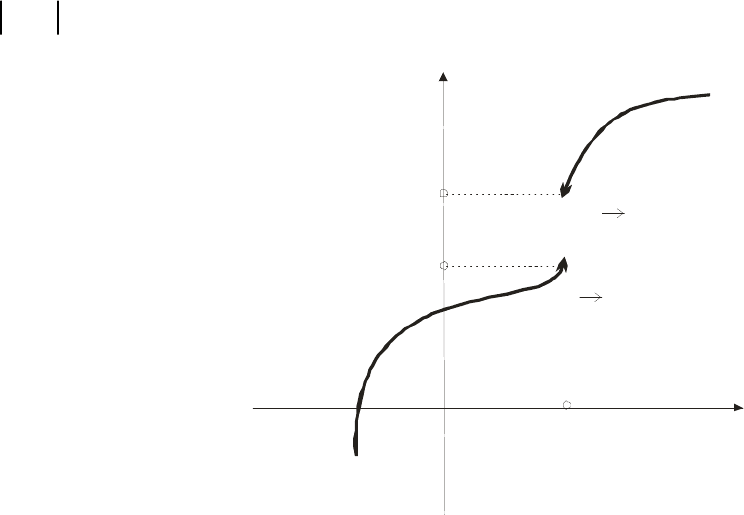
42
Функция называется непрерывной на некотором множестве Х, если
она непрерывна во всех точках этого множества.
Точки, в которых нарушается непрерывность функции, называются
точками разрыва функции. Различают разрывы первого рода и второго
рода.
Говорят, что функция
(
)
y f x
=
в точке
x a
=
имеет разрыв первого
рода (рис.2), его еще называют конечный скачок, если:
1. Существует предел функции при
x
, стремящемся к
a
слева, т.е.
существует
(
)
0
lim
x a
f x b
→ −
=
;
2. Существует предел функции при
x
, стремящемся к
a
справа, т.е.
существует
(
)
+0
lim
x a
f x c
→
=
;
3. Но эти пределы не равны, т.е.
b c
≠
. Абсолютная величина разности
b c
−
, называется скачком функции
(
)
y f x
=
в точке
x a
=
.
x
y
a
b
c
a - точка разрыва
1-го рода
lim f(x) = b
lim f(x) = c
x a - 0
x a + 0
|b-c| -
x=a
скачок
функции
в точке
Рис. 2. Разрыв функции 1-го рода:
(
)
0
lim
x a
f x b
→ −
=
,
(
)
0
lim
x a
f x c
→ +
=
,
b c
≠
Говорят, что функция
(
)
y f x
=
имеет в точке
x a
=
разрыв второго
рода, если не существует или равен
±∞
хотя бы один из односторонних
пределов при
x a
→
, и следовательно не существует
(
)
lim
x a
f x
→
(рис. 3).
