Tan S.T. Finite Mathematics for the Managerial, Life, and Social Sciences
Подождите немного. Документ загружается.


222 4 LINEAR PROGRAMMING: AN ALGEBRAIC APPROACH
xyzu√ wP Constant
2 1 11000 180
1 3 20100 300
2 1 20010 240
6 5 40001 0
xy zu√ wP Constant
1 0.5 0.50.5000 90
1 3 2 0 100 300
2 1 2 0 010 240
6 5 40001 0
To solve this problem, we introduce slack variables u, √,
and w and use the simplex method, obtaining the following
sequence of simplex tableaus:
The Simplex Method: Solving Maximization Problems
Graphing Utility
A graphing utility can be used to solve a linear programming problem by the simplex
method, as illustrated in Example 1.
EXAMPLE 1
(Refer to Example 5, Section 4.1.) The problem reduces to the fol-
lowing linear programming problem:
Maximize P 6x 5y 4z
subject to 2x y z 180
x 3y 2z 300
2x y 2z 240
x 0, y 0, z 0
With u, √, and w as slack variables, we are led to the following sequence of simplex
tableaus, where the first tableau is entered as the matrix A:
The last tableau is final, and we see that x 150, y 140,
and P 2020. Therefore, LaCrosse should make 150
model-A grates and 140 model-B grates this week. The
profit will be $2020.
Ratio
—
1200
3
400
720
3
240
Pivot
씮
row
앖
Pivot column
R
2
3R
1
⎯⎯⎯→
R
4
8R
1
Pivot row 씮
앖
Pivot column
Ratio
150
1
150
480
2
240
240
2/3
360
R
1
⎯→
1
3
R
1
R
3
⎯⎯⎯→
R
2
2R
3
R
4
R
3
2
3
2
3
xyu√ wP Constant
2 31000 720
4 30100 1200
1 00010 150
6 80001 0
xyu√ wPConstant
2
3
1
1
3
000 240
4 30100 1200
1 00010 150
6 80001 0
xy u√ wP Constant
2
3
1
1
3
0 0 0 240
201100 480
10 00 10 150
2
3
0
8
3
0 0 1 1920
xy u√ wP Constant
01
1
3
0
2
3
0 140
00112 0 180
10 00 10 150
00
8
3
0
2
3
1 2020
USING
TECHNOLOGY
Ratio
240
2
120
300
1
300
180
2
90
Pivot
씮
row
*rowÓ
1
2
, A, 1Ô 䉴 B
⎯⎯⎯⎯⎯⎯⎯→
앖
Pivot
column
*rowⴙ(1, B, 1, 2) 䉴 C
⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯→
*rowⴙ(2, C, 1, 3) 䉴 B
*rowⴙ(6, B, 1, 4) 䉴 C
87533_04_ch4_p201-256 1/30/08 9:52 AM Page 222

4.1 THE SIMPLEX METHOD: STANDARD MAXIMIZATION PROBLEMS 223
The final simplex tableau is the same as the one obtained earlier. We see that
x 48, y 84, z 0, and P 708. Hence, Ace Novelty should produce 48 type-A
souvenirs, 84 type-B souvenirs, and no type-C souvenirs—resulting in a profit of
$708 per day.
Excel
Solver is an Excel add-in that is used to solve linear programming problems. When
you start the Excel program, check the Tools menu for the Solver command. If it
is not there, you will need to install it. (Check your manual for installation
instructions.)
EXAMPLE 2
Solve the following linear programming problem:
Maximize P 6x 5y 4z
subject to 2x y z 180
x 3y 2z 300
2x y 2z 240
x 0, y 0, z 0
Solution
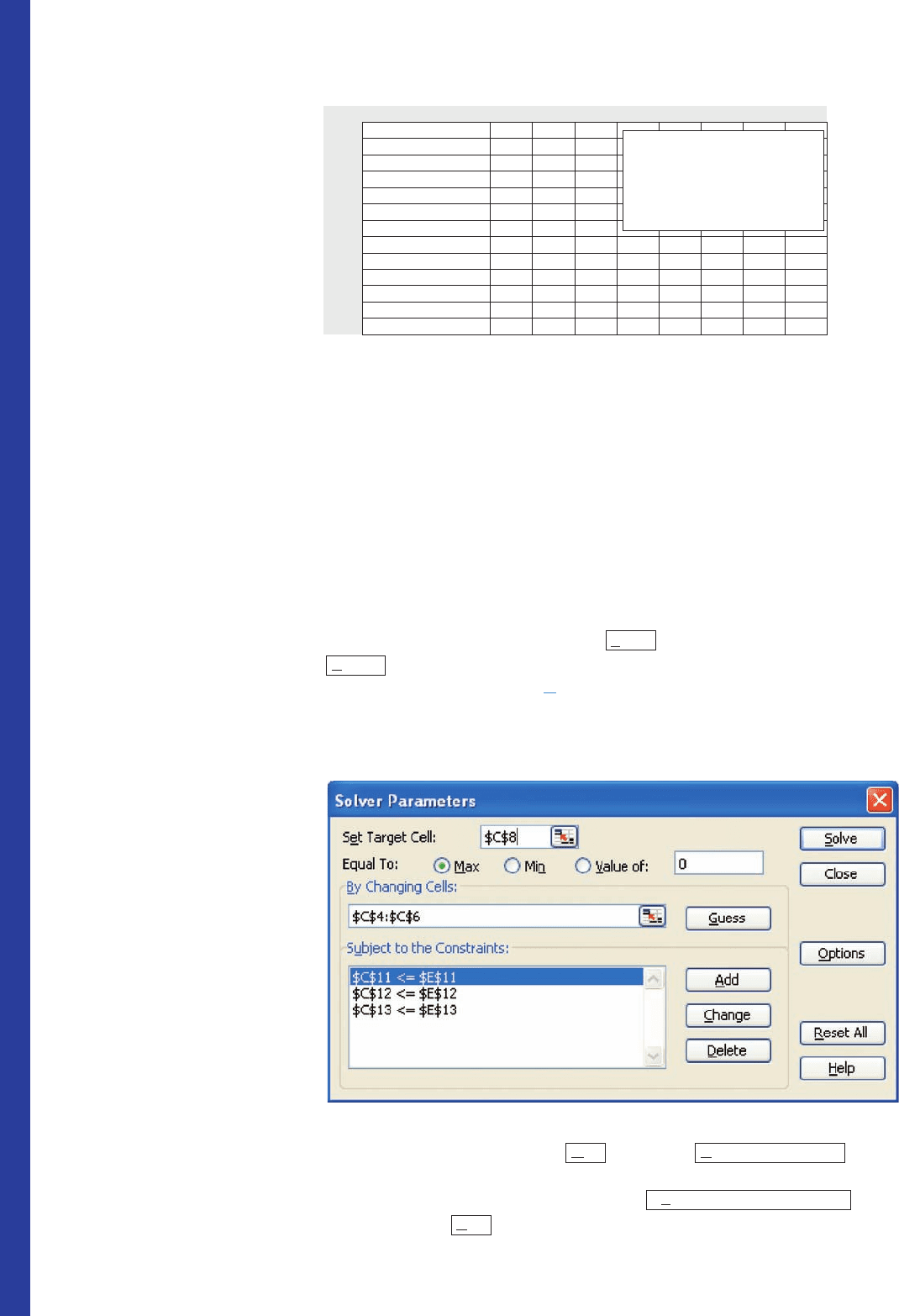
1. Enter the data for the linear programming problem onto a spreadsheet. Enter the
labels shown in column A and the variables with which we are working under
Decision Variables in cells B4:B6, as shown in Figure T1. This optional step will
help us organize our work.
xy z u√ wP Constant
1 0.5 0.5 0.5000 90
0 2.5 1.5 0.5 1 0 0 210
00 1 1 010 60
0 2 1 3 0 0 1 540
(continued)
Ratio
210
2.5
84
90
0.5
180
*rowÓ
2
1
.5
, C, 2Ô 䉴 B
⎯⎯⎯⎯⎯⎯⎯→
앖
Pivot
column
Pivot
씮
row
*rowⴙ(0.5, B, 2, 1) 䉴 C
———————————씮
*rowⴙ(2, C, 2, 4) 䉴 B
Note: Boldfaced words/characters enclosed in a box (for example, ) indicate that an action (click, select, or press)
is required. Words/characters printed blue (for example, Chart sub-t
ype:) indicate words/characters that appear on the screen.
Words/characters printed in a typewriter font (for example, =(—2/3)*A2+2) indicate words/characters that need to be typed
and entered.
Enter
xy z u√ wP Constant
1 0.5 0.5 0.5 0 0 0 90
0 1 0.6 0.2 0.4 0 0 84
00 11010 60
0 2 1 3001 540
xy z u √ wP Constant
1 0 0.2 0.6 0.2 0 0 48
0 1 0.6 0.2 0.4 0 0 84
001 10 10 60
0 0 0.2 2.6 0.8 0 1 708
87533_04_ch4_p201-256 1/30/08 9:52 AM Page 223
224 4 LINEAR PROGRAMMING: AN ALGEBRAIC APPROACH
For the moment, the cells that will contain the values of the variables (C4:C6) are
left blank. In C8 type the formula for the objective function: =6*C4+5*C5+
4*C6. In C11 type the formula for the left-hand side of the first constraint:
=2*C4+C5+C6. In C12 type the formula for the left-hand side of the second
constraint: =C4+3*C5+2*C6. In C13 type the formula for the left-hand side of
the third constraint: =2*C4+C5+2*C6. Zeros will then appear in cell B8 and
cells C11:C13. In cells D11:D13, type <= to indicate that each constraint is of the
form . Finally, in cells E11:E13, type the right-hand value of each constraint—
in this case, 180, 300, and 240, respectively. Note that we need not enter the
nonnegativity constraints x 0, y 0, and z 0. The resulting spreadsheet is
shown in Figure T1, where the formulas that were entered for the objective func-
tion and the constraints are shown in the comment box.
2. Use Solver to solve the problem. Click on the menu bar and then click
. The Solver Parameters dialog box will appear.
a. The pointer will be in the Set
Target Cell: box (refer to Figure T2). High-
light the cell on your spreadsheet containing the formula for the objective
function—in this case, C8.
Then, next to Equal To: select . Select the box
and highlight the cells in your spreadsheet that will contain the values of the
variables—in this case, C4:C6. Select the box
and then click . The Add Constraint dialog box will appear (Figure T3).
Add
Subject to the Constraints:
By Changing Cells:Max
S
olver
Tools
ABCDEFGHI
1
Maximization Problem
2
3
Decision Variables
4
5
6
7
8
Objective Function
9
10
Constraints
11
180
12
300
13
0
240
Formulas for indicated cells
C8: = 6
*
C4 + 5
*
C5 + 4
*
C6
C11: = 2
*
C4 + C5 + C6
C12: = C4 + 3
*
C5 + 2
*
C6
C13: = 2
*
C4 + C5 + 2
*
C6
z
y
x
<=
0
<=
0
0
<=
FIGURE T1
Setting up the spreadsheet for Solver
FIGURE T2
The completed Solver Parameters dialog
box
87533_04_ch4_p201-256 1/30/08 9:52 AM Page 224
4.1 THE SIMPLEX METHOD: STANDARD MAXIMIZATION PROBLEMS 225
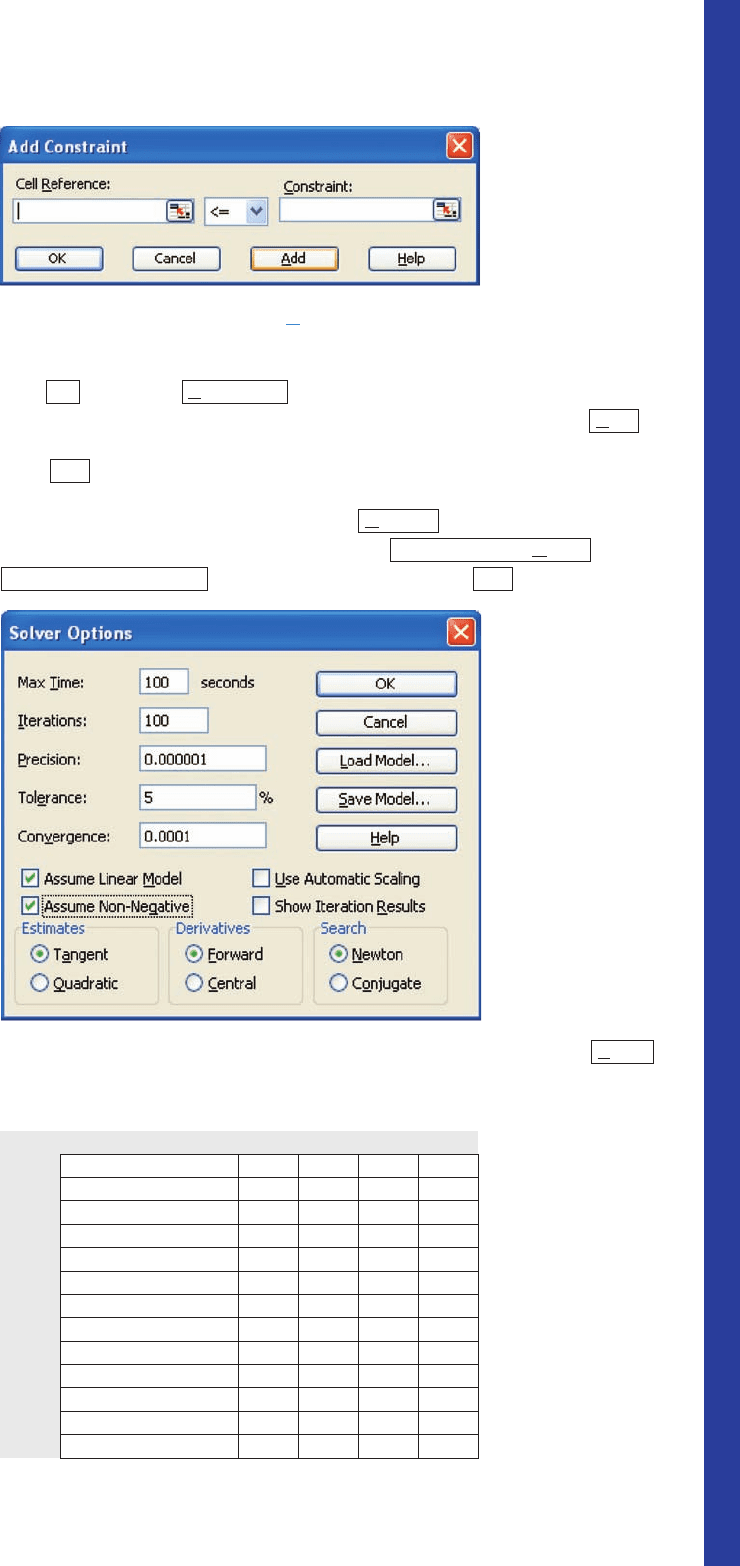
b. The pointer will appear in the Cell Reference: box. Highlight the cells on your
spreadsheet that contain the formula for the left-hand side of the first constraint—
in this case, C11. Next, select the symbol for the appropriate constraint—in this
case, . Select the box and highlight the value of the right-hand
side of the first constraint on your spreadsheet—in this case, 180. Click
and then follow the same procedure to enter the second and third constraint.
Click . The resulting Solver Parameters dialog box shown in Figure T2 will
appear.
c. In the Solver Parameters dialog box, click (see Figure T2). In the
Solver Options dialog box that appears, select and
constraints (Figure T4). Click .
d. In the Solver Parameters dialog box that appears (see Figure T2), click .
A Solver Results dialog box will then appear and at the same time the answers
will appear on your spreadsheet (Figure T5).
ABCDE
1
Maximization Problem
2
3
Decision Variables
4
5
6
7
8
Objective Function
9
10
Constraints
11
180
12
300
13
240
240
z
y
x
<=
300
<=
180
708
0
84
48
<=
Solve
OK
Assume Non-Negative
Assume Linear Model
Options
OK
Add
Constraint:<=
FIGURE T3
The Add Constraint dialog box
FIGURE T4
The Solver Options dialog box
(continued)
FIGURE
T5
Completed spreadsheet after using Solver
87533_04_ch4_p201-256 1/30/08 9:52 AM Page 225

226 4 LINEAR PROGRAMMING: AN ALGEBRAIC APPROACH
3. Read off your answers. From the spreadsheet, we see that the objective function
attains a maximum value of 708 (cell C8) when x 48, y 84, and z 0 (cells
C4:C6).
Solve the linear programming problems.
1. Maximize P 2x 3y 4z 2w
subject to x 2y 3z 2w 6
2x 4y z w 4
3x 2y 2z 3w 12
x 0, y 0, z 0, w 0
2. Maximize P 3x 2y 2z w
subject to 2 x y z 2w 8
2x y 2z 3w 20
x y z 2w 8
4x 2y z 3w 24
x 0, y 0, z 0, w 0
3. Maximize P x y 2z 3w
subject to 3 x 6y 4z 2w 12
x 4y 8z 4w 16
2x y 4z w 10
x 0, y 0, z 0, w 0
4. Maximize P 2x
4y 3z 5w
subject to x 2y 3z 4w 8
2x 2y 4z 6w 12
3x 2y z 5w 10
2x 8y 2z 6w 24
x 0, y 0, z 0, w 0
TECHNOLOGY EXERCISES
4.2 The Simplex Method: Standard Minimization Problems
Minimization with ⱕ Constraints
In the last section, we developed a procedure, called the simplex method, for solving
standard linear programming problems. Recall that a standard maximization problem
satisfies three conditions:
1. The objective function is to be maximized.
2. All the variables involved are nonnegative.
3. Each linear constraint may be written so that the expression involving the variables
is less than or equal to a nonnegative constant.
In this section, we see how the simplex method may be used to solve certain
classes of problems that are not necessarily standard maximization problems. In par-
ticular, we see how a modified procedure may be used to solve problems involving the
minimization of objective functions.
We begin by considering the class of linear programming problems that calls for
the minimization of objective functions but otherwise satisfies Conditions 2 and 3 for
standard maximization problems. The method used to solve these problems is illus-
trated in the following example.
EXAMPLE 1
Minimize C 2x 3y
subject to 5x 4y 32
x 2y 10
x 0, y 0
Solution
This problem involves the minimization of the objective function and is
accordingly not a standard maximization problem. Note, however, that all other
87533_04_ch4_p201-256 1/30/08 9:52 AM Page 226

4.2 THE SIMPLEX METHOD: STANDARD MINIMIZATION PROBLEMS 227
conditions for a standard maximization problem hold true. To solve a problem of
this type, we observe that minimizing the objective function C is equivalent to maxi-
mizing the objective function P C. Thus, the solution to this problem may be
found by solving the following associated standard maximization problem: Maxi-
mize P 2x 3y subject to the given constraints. Using the simplex method with u
and √ as slack variables, we obtain the following sequence of simplex tableaus:
The last tableau is in final form. The solution to the standard maximization problem
associated with the given linear programming problem is x 4, y 3, and P 17,
so the required solution is given by x 4, y 3, and C 17. You may verify
that the solution is correct by using the method of corners.
The Dual Problem
Another special class of linear programming problems we encounter in practical appli-
cations is characterized by the following conditions:
1. The objective function is to be minimized.
2. All the variables involved are nonnegative.
3. All other linear constraints may be written so that the expression involving the vari-
ables is greater than or equal to a constant.
Such problems are called standard minimization problems.
xyu√ P Constant
5 4100 32
1 2010 10
2 3001 0
xyu√ P Constant
5 4100 32
1
2
10
1
2
05
2 3001 0
xyu √ P Constant
30120 12
1
2
10
1
2
05
1
2
00
3
2
115
xyu √ P Constant
10
1
3
2
3
04
1
2
10
1
2
05
1
2
00
3
2
115
xy u √ P Constant
10
1
3
2
3
04
01
1
6
5
6
03
00
1
6
7
6
117
Ratio
10
2
5
32
4
8
Pivot
씮
row
앖
Pivot
column
R
2
⎯→
1
2
R
1
4R
2
⎯⎯⎯→
R
3
3R
2
앖
Pivot
column
Ratio
5
1/2
10
12
3
4
Pivot
row
—
씮
R
1
⎯→
1
3
R
2
R
1
⎯⎯⎯→
R
3
R
1
1
2
1
2
Explore & Discuss
Refer to Example 1.
1. Sketch the feasible set S for
the linear programming
problem.
2. Solve the problem using the
method of corners.
3. Indicate on S the corner
points corresponding to each
iteration of the simplex pro-
cedure and trace the path
leading to the optimal
solution.
87533_04_ch4_p201-256 1/30/08 9:52 AM Page 227
228 4 LINEAR PROGRAMMING: AN ALGEBRAIC APPROACH
A convenient method for solving this type of problem is based on the following
observation. Each maximization linear programming problem is associated with a
minimization problem, and vice versa. For the purpose of identification, the given
problem is called the primal problem; the problem related to it is called the dual
problem. The following example illustrates the technique for constructing the dual of
a given linear programming problem.
EXAMPLE 2
Write the dual problem associated with the following problem:
Minimize the objective function C 6x 8y
subject to 40x 10y 2400
10x 15y 2100
5x 15y 1500
x 0, y 0000
Solution
We first write down the following tableau for the given primal problem:
Next, we interchange the columns and rows of the foregoing tableau and head the three
columns of the resulting array with the three variables u, √, and w, obtaining the tableau
Interpreting the last tableau as if it were part of the initial simplex tableau for a stan-
dard maximization problem—with the exception that the signs of the coefficients
pertaining to the objective function are not reversed—we construct the required dual
problem as follows:
Maximize the objective function P 2400u 2100√ 1500w
subject to 40u 10√ 5w 6
10u 15√ 15w 8
u 0, √ 0, w 0
The connection between the solution of the primal problem and that of the dual prob-
lem is given by the following theorem. The theorem, attributed to John von Neumann
(1903–1957), is stated without proof.
THEOREM 1
The Fundamental Theorem of Duality
A primal problem has a solution if and only if the corresponding dual problem
has a solution. Furthermore, if a solution exists, then:
a. The objective functions of both the primal and the dual problem attain the
same optimal value.
b. The optimal solution to the primal problem appears under the slack variables
in the last row of the final simplex tableau associated with the dual problem.
Primal
problem
xyConstant
40 10 2400
10 15 2100
5 15 1500
68
u √ w Constant
40 10 5 6
10 15 15 8
2400 2100 1500
Dual
problem
87533_04_ch4_p201-256 1/30/08 9:52 AM Page 228
4.2 THE SIMPLEX METHOD: STANDARD MINIMIZATION PROBLEMS 229
Armed with this theorem, we will solve the problem posed in Example 2.
EXAMPLE 3
Complete the solution to the problem posed in Example 2.
Solution
Observe that the dual problem associated with the given (primal) prob-
lem is a standard maximization problem. The solution may thus be found using the
simplex algorithm. Introducing the slack variables x and y, we obtain the system of
linear equations
40u 10√ 5w x 6
10u 15√ 15w y 8
2400u 2100√ 1500w P 0
Continuing with the simplex algorithm, we obtain the following sequence of simplex
tableaus:
The last tableau is final. The fundamental theorem of duality tells us that the
solution to the primal problem is x 30 and y 120 with a minimum value for C
of 1140. Observe that the solution to the dual (maximization) problem may be read
from the simplex tableau in the usual manner: u , √ , w 0, and P 1140.
13
25
1
50
u √ wxyPConstant
40 10 5100 6
10 15 15010 8
2400 2100 1500 0 0 1
冨
0
u √ wxyPConstant
1
1
4
1
8
4
1
0
00
2
3
0
10 15 15 0 1 0 8
2400 2100 1500 0 0 1
冨
0
u √ wxyPConstant
1
1
4
1
8
4
1
0
00
2
3
0
0
2
2
5
5
4
5
1
4
10
1
2
3
0 1500 1200 60 0 1
冨
360
u √ wxyPConstant
1
1
4
1
8
4
1
0
00
2
3
0
01
1
1
1
0
5
1
0
2
2
5
0
1
2
3
5
0 1500 1200 60 0 1
冨
360
u √ wxyPConstant
10
2
3
0
1
3
00
5
1
0
0
5
1
0
01
1
1
1
0
5
1
0
2
2
5
0
1
2
3
5
0 0 450 30 120 1
冨
1140
Pivot
씮
row
앖
Pivot
column
R
2
10R
1
⎯⎯⎯⎯⎯→
R
3
2400R
1
Ratio
8
10
4
5
6
40
3
20
Ratio
13/2
25/2
13
25
3/20
1/4
3
5
Solution for the
primal problem
R
2
⎯→
2
25
R
1
⎯→
1
40
R
1
R
2
⎯⎯⎯⎯⎯→
R
3
1500R
2
1
4
Pivot
row
앖
Pivot
column
씮
87533_04_ch4_p201-256 1/30/08 9:52 AM Page 229

Note that the maximum value of P is equal to the minimum value of C, as guaran-
teed by the fundamental theorem of duality. The solution to the primal problem
agrees with the solution of the same problem solved in Section 3.3, Example 2,
using the method of corners.
Notes
1. We leave it to you to demonstrate that the dual of a standard minimization problem
is always a standard maximization problem provided that the coefficients of the
objective function in the primal problem are all nonnegative. Such problems can
always be solved by applying the simplex method to solve the dual problem.
2. Standard minimization problems in which the coefficients of the objective function
are not all nonnegative do not necessarily have a dual problem that is a standard
maximization problem.
EXAMPLE 4
Minimize C 3x 2y
subject to 8x y 80
8x 5y 240
x 5y 100
x 0, y 0
Solution
We begin by writing the dual problem associated with the given primal
problem. First, we write down the following tableau for the primal problem:
Next, interchanging the columns and rows of this tableau and heading the three
columns of the resulting array with the three variables, u, √, and w, we obtain the
tableau
Interpreting the last tableau as if it were part of the initial simplex tableau for a standard
maximization problem—with the exception that the signs of the coefficients pertaining
to the objective function are not reversed—we construct the dual problem as follows:
Maximize the objective function P 80u 240√ 100w subject to the constraints
8u 8√ w 3
u 5√ 5w 2
where u 0, √ 0, and w 0. Having constructed the dual problem, which is a
standard maximization problem, we now solve it using the simplex method. Intro-
ducing the slack variables x and y, we obtain the system of linear equations
8u 8√ w x 3
u 5√ 5w y 2
80u 240√ 100w P 0
230 4 LINEAR PROGRAMMING: AN ALGEBRAIC APPROACH
xy Constant
81 80
8 5 240
1 5 100
32
u √ w Constant
881 3
155 2
80 240 100
87533_04_ch4_p201-256 1/30/08 9:52 AM Page 230
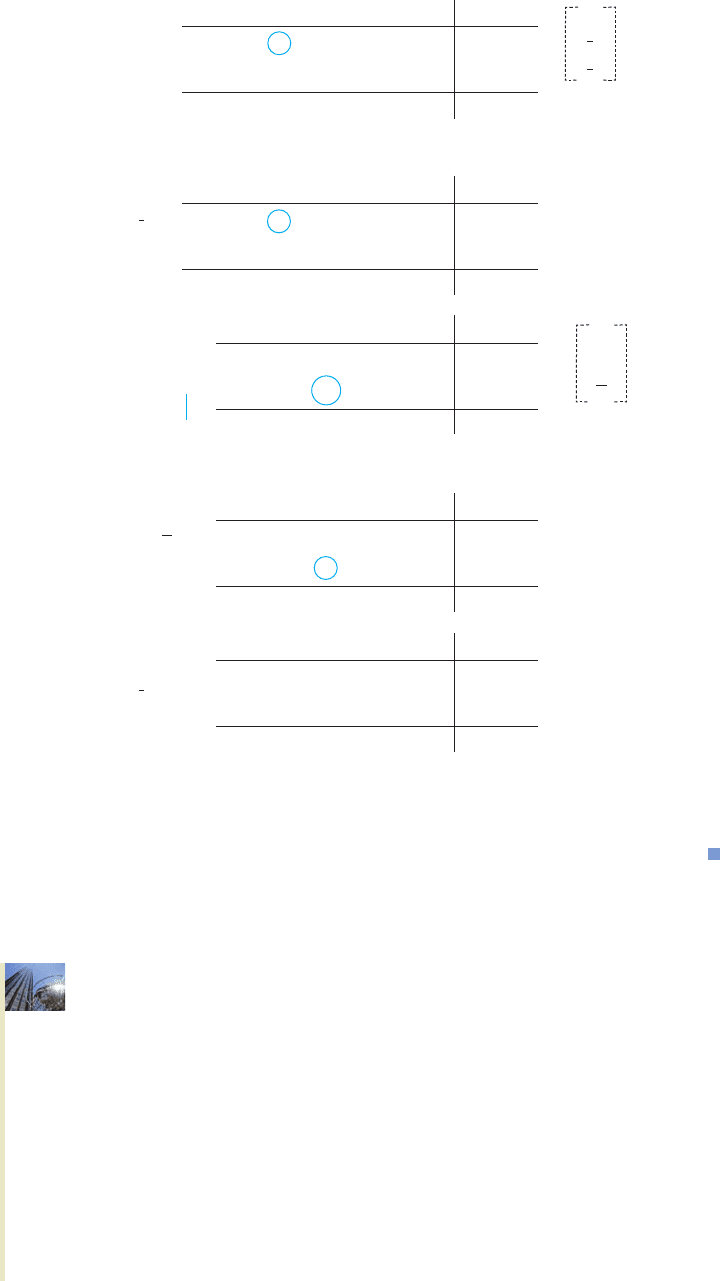
Continuing with the simplex algorithm, we obtain the following sequence of simplex
tableaus:
The last tableau is final. The fundamental theorem of duality tells us that the solution
to the primal problem is x 20 and y 16 with a minimum value for C of 92.
Our last example illustrates how the warehouse problem posed in Section 3.2 may be
solved by duality.
APPLIED EXAMPLE 5
A Warehouse Problem Complete the solu-
tion to the warehouse problem given in Section 3.2, Example 4 (page 167).
Minimize
C 20x
1
8x
2
10x
3
12x
4
22x
5
18x
6
(13)
subject to
x
1
x
2
x
3
400
x
4
x
5
x
6
600
x
1
x
4
200
x
2
x
5
300
(14)
x
3
x
6
400
x
1
0, x
2
0, . . . , x
6
0
4.2 THE SIMPLEX METHOD: STANDARD MINIMIZATION PROBLEMS 231
u √ wx y P Constant
8 8 1100 3
1 5 5010 2
80 240 100001 0
u √ wx y P Constant
11
1
8
1
8
00
3
8
1 5 5010 2
80 240 100001 0
u √ wxyPConstant
11
1
8
1
8
00
3
8
40
3
8
5
5
8
10
1
8
160 0 70 30 0 1 90
u √ wxyPConstant
11
1
8
1
8
00
3
8
3
3
2
5
01
1
7
3
8
5
0
3
1
5
160 0 70 30 0 1 90
u √ wx yPConstant
3
3
9
5
10
1
7
3
1
5
0
1
3
3
5
3
3
2
5
01
1
7
3
8
5
0
3
1
5
96 0 0 20 16 1 92
Pivot
씮
row
앖
Pivot column
Ratio
2
5
3
8
Ratio
3
1
35
R
2
5R
1
⎯⎯⎯⎯→
R
3
240R
1
Pivot
row
씮
앖
Pivot column
Solution for the
primal problem
R
1
⎯→
1
8
R
2
⎯→
8
35
R
1
R
2
⎯⎯⎯⎯→
R
3
70R
2
1
8
87533_04_ch4_p201-256 1/30/08 9:52 AM Page 231
