Tan S.T. Finite Mathematics for the Managerial, Life, and Social Sciences
Подождите немного. Документ загружается.


242 4 LINEAR PROGRAMMING: AN ALGEBRAIC APPROACH
Section 4.1 showed how we can use the simplex method to solve standard maximization
problems; Section 4.2 showed how, thanks to duality, we can use it to solve standard min-
imization problems provided that the coefficients in the objective function are all non-
negative.
In this section, we see how the simplex method can be incorporated into a method
for solving nonstandard problems—problems that do not fall into either of the two
previous categories. We begin by recalling the characteristics of standard problems.
Standard Maximization Problem
1. The objective function is to be maximized.
2. All variables involved in the problem are nonnegative.
3. Each linear constraint may be written so that the expression involving the variables
is less than or equal to a nonnegative constant.
Standard Minimization Problem (Restricted Version—See Condition 4)
1. The objective function is to be minimized.
2. All variables involved in the problem are nonnegative.
3. Each linear constraint may be written so that the expression involving the variables
is greater than or equal to a constant.
4. All coefficients in the objective function are nonnegative.
Note
Recall that if all coefficients in the objective function are nonnegative, then a
standard minimization problem can be solved by using the simplex method to solve
the associated dual problem.
We now give some examples of linear programming problems that do not fit into these
two categories of problems.
EXAMPLE 1
Explain why the following linear programming problem is not a
standard maximization problem.
Maximize P x 2y
subject to 4x 3y 18
x 3y 3
x 0, y 0
Solution
This is not a standard maximization problem because the second con-
straint,
x 3y 3
violates Condition 3. Observe that multiplying both sides of this inequality by 1
yields
x 3y 3 Recall that multiplying both sides of an inequality by
a negative number reverses the inequality sign.
Now the last equation still violates Condition 3 because the constant on the right is
negative.
Observe that the constraints in Example 1 involve both less than or equal to con-
straints () and greater than or equal to constraints (). Such constraints are called
mixed constraints. We will solve the problem posed in Example 1 later.
4.3 The Simplex Method: Nonstandard Problems
87533_04_ch4_p201-256 1/30/08 9:52 AM Page 242

EXAMPLE 2
Explain why the following linear programming problem is not a
restricted standard minimization problem.
Minimize C 2x 3y
subject to x y 5
x 3y 9
2x y 2
x 0, y 0
Solution
Observe that the coefficients in the objective function C are not all
nonnegative. Also, Condition 3 is violated. Therefore, the problem is not a
restricted standard minimization problem. By constructing the dual problem, you
can convince yourself that the latter is not a standard maximization problem and
thus cannot be solved using the methods described in Sections 4.1 and 4.2.
Again, we will solve this problem later.
EXAMPLE 3
Explain why the following linear programming problem is not a
standard maximization problem. Show that it cannot be rewritten as a restricted stan-
dard minimization problem.
Maximize P x 2y
subject to 2x 3y 12
x 3y 3
x 0, y 00
Solution
The constraint equation x 3y 3 is equivalent to the two inequal-
ities
x 3y 3 and x 3y 3
If we multiply both sides of the second inequality by 1, then it can be written in
the form
x 3y 3
Therefore, the two given constraints are equivalent to the three constraints
2x 3y 12
x 3y 3
x 3y 3
The third inequality violates Condition 3 for a standard maximization problem.
Next, we see that the given problem is equivalent to the following:
Minimize C x 2y
subject to 2 x 3y 12
x 3y 3
x 3y 3
x 0, y 0
Since the coefficients of the objective function are not all nonnegative, we conclude
that the given problem cannot be rewritten as a restricted standard minimization
problem. You will be asked to solve this problem in Exercise 11.
4.3 THE SIMPLEX METHOD: NONSTANDARD PROBLEMS 243
87533_04_ch4_p201-256 1/30/08 9:52 AM Page 243
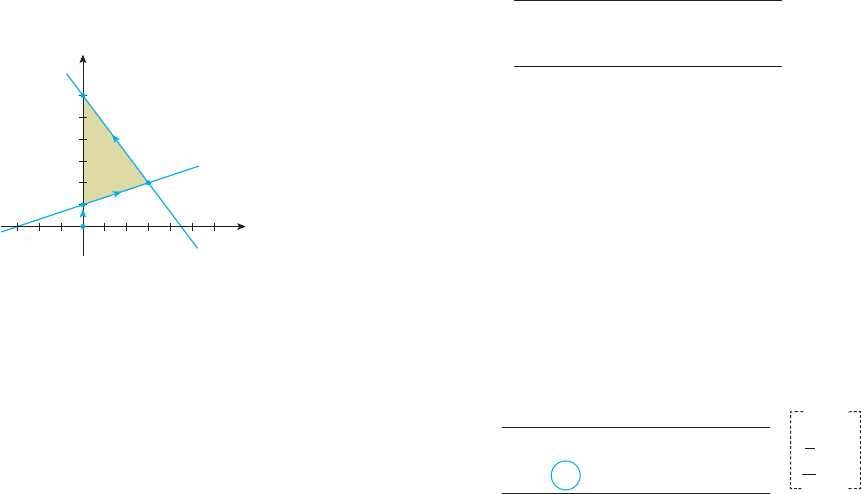
The Simplex Method for Solving Nonstandard Problems
To describe a technique for solving nonstandard problems, let’s consider the problem
of Example 1:
Maximize P x 2y
subject to 4x 3y 18
x 3y 3
x 0, y 00
As a first step, we rewrite the constraints so that the second constraint involves a
constraint. As in Example 1, we obtain
4x 3y 18
x 3y 3
x 0, y 0
Disregarding the fact that the constant on the right of the second inequality is nega-
tive, let’s attempt to solve the problem using the simplex method for problems in stan-
dard form. Introducing the slack variables u and √ gives the system of linear equations
4x 3y u 18
x 3y √ 3
x 2y P 0
The initial simplex tableau is
Interpreting the tableau in the usual fashion, we see that
x 0 y 0 u 18 √ 3 P 0
Since the value of the slack variable √ is negative, we see that this cannot be a feasi-
ble solution (remember, all variables must be nonnegative). In fact, you can see from
Figure 6 that the point (0, 0) does not lie in the feasible set associated with the given
problem. Since we must start from a feasible point when using the simplex method for
problems in standard form, we see that this method is not applicable at this juncture.
Let’s find a way to bring us from the nonfeasible point (0, 0) to any feasible point,
after which we can switch to the simplex method for problems in standard form. This
can be accomplished by pivoting as follows. Referring to the tableau
notice the negative number 3 lying in the column of constants and above the lower
horizontal line. Locate any negative number to the left of this number (there must
always be at least one such number if the problem has a solution). For the problem
under consideration there is only one such number, the number 3 in the y-column.
244 4 LINEAR PROGRAMMING: AN ALGEBRAIC APPROACH
FIGURE 6
S is the feasible set for the problem.
y
x
0
(0, 1)
(0, 6)
(3, 2)
– x
S
+ 3y = 3
4x + 3y = 18
xyu√ P Constant
4 3100 18
1 3010 3
1 2001
冨
0
xyu√ P Constant
4 3100 18
1 3010 3
1 2001
冨
0
Pivot
씮
row
앖
Pivot column
Ratio
3
3
1
18
3
6
87533_04_ch4_p201-256 1/30/08 9:52 AM Page 244
This column is designated as the pivot column. To find the pivot element, we form the
positive ratios of the numbers in the column of constants to the corresponding num-
bers in the pivot column (above the last row). The pivot row is the row corresponding
to the smallest ratio, and the pivot element is the element common to both the pivot
row and the pivot column (the number circled in the foregoing tableau). Pivoting
about this element, we have
Interpreting the last tableau in the usual fashion, we see that
x 0 y 1 u 15 √ 0 P 2
Observe that the point (0, 1) is a feasible point (see Figure 6). Our iteration has
brought us from a nonfeasible point to a feasible point in one iteration. Observe, too,
that all the constants in the column of constants are now nonnegative, reflecting the
fact that (0, 1) is a feasible point, as we have just noted.
We can now use the simplex method for problems in standard form to complete
the solution to our problem.
4.3 THE SIMPLEX METHOD: NONSTANDARD PROBLEMS 245
R
1
3R
2
⎯⎯⎯→
R
3
2R
2
R
2
⎯→
1
3
xyu√ P Constant xyu √ P Constant
4 31 00 18 501 10 15
1
3
10
1
3
01
1
3
10
1
3
01
1 20 01 0
5
3
00
2
3
12
xyu √ P Constant
501 10 15
1
3
10
1
3
01
5
3
00
2
3
12
xyu √ P Constant
10
1
5
1
5
03
1
3
10
1
3
01
5
3
00
2
3
12
xy u √ P Constant
10
1
5
1
5
03
01
1
1
5
1
4
5
02
00
1
3
1
3
17
xy u √ P Constant xyu√ P Constant
50 1 1 0 15 50110 15
01
1
1
5
1
4
5
02
4
3
1
1
3
00 6
00
1
3
1
3
17
5
3
0
2
3
01 12
Ratio
3
—
Pivot
씮
row
앖
Pivot
column
Ratio
15
—
Pivot
row
—
씮
앖
Pivot
column
5R
1
⎯→
R
1
⎯→
1
5
R
2
R
1
⎯⎯⎯→
R
3
R
1
5
3
1
3
R
2
R
1
⎯⎯⎯→
R
3
R
1
1
3
4
15
87533_04_ch4_p201-256 1/30/08 9:52 AM Page 245

246 4 LINEAR PROGRAMMING: AN ALGEBRAIC APPROACH
All entries in the last row are nonnegative and so the tableau is final. We see that the
optimal solution is
x 0 y 6 u 0 √ 15 P 12
Observe that the maximum of P occurs at (0, 6) (see Figure 6). The arrows indicate
the path that our search for the maximum of P has taken us on.
Before looking at further examples, let’s summarize the method for solving non-
standard problems.
We now apply the method to solve the nonstandard problem posed in Example 2.
EXAMPLE 4
Solve the problem of Example 2:
Minimize C 2x 3y
subject to x y 5
x 3y 9
2x y 2
x 0, y 0
Solution
We first rewrite the problem as a maximization problem with constraints
using , which gives the following equivalent problem:
Maximize P C 2x 3y
subject to x y 5
x 3y 9
2x y 2
x 0, y 0
Introducing slack variables u, √, and w and following the procedure for solving
nonstandard problems outlined previously, we obtain the following sequence of
tableaus:
The Simplex Method for Solving Nonstandard Problems
1. If necessary, rewrite the problem as a maximization problem (recall that min-
imizing C is equivalent to maximizing C).
2. If necessary, rewrite all constraints (except x 0, y 0, z 0, . . .) using
less than or equal to () inequalities.
3. Introduce slack variables and set up the initial simplex tableau.
4. Scan the upper part of the column of constants of the tableau for negative
entries.
a. If there are no negative entries, complete the solution using the simplex
method for problems in standard form.
b. If there are negative entries, proceed to step 5.
5. a. Pick any negative entry in a row in which a negative entry in the column
of constants occurs. The column containing this entry is the pivot column.
b. Compute the positive ratios of the numbers in the column of constants to
the corresponding numbers in the pivot column (above the last row). The
pivot row corresponds to the smallest ratio. The intersection of the pivot
column and the pivot row determines the pivot element.
c. Pivot the tableau about the pivot element. Then return to step 4.
87533_04_ch4_p201-256 1/30/08 9:52 AM Page 246
All the entries in the last row are nonnegative and hence the tableau is final. We see
that the optimal solution is
x 1 y 4 u 0 √ 4 w 0 C P 10
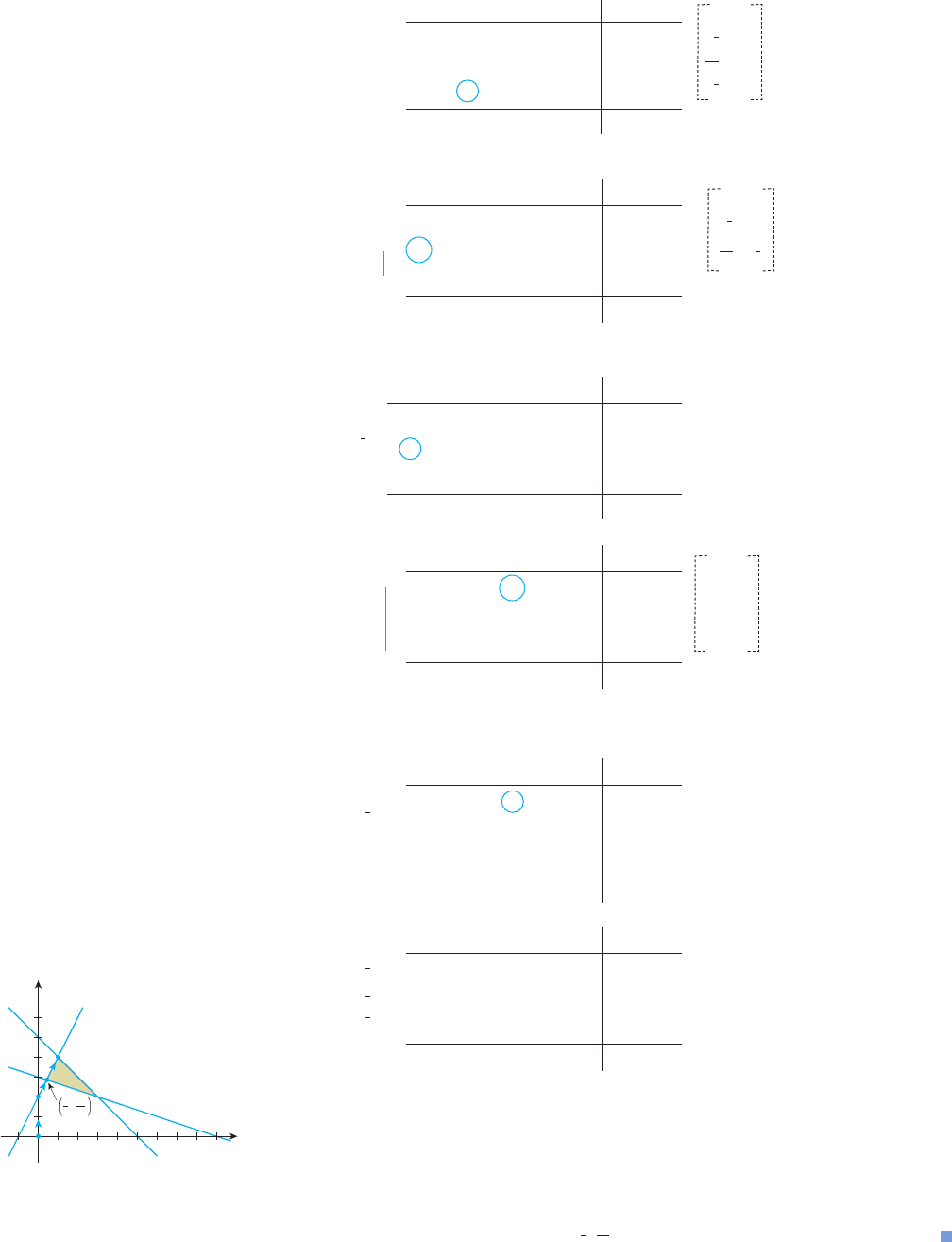
The feasible set S for this problem is shown in Figure 7. The path leading from the
nonfeasible initial point (0, 0) to the optimal point (1, 4) goes through the nonfeasi-
ble point (0, 2) and the feasible point ( ), in that order.
3
7
,
20
7
4.3 THE SIMPLEX METHOD: NONSTANDARD PROBLEMS 247
xyu√ wP Constant
111000 5
1 30100 9
2 10010 2
2 30001 0
xyu √ wP Constant
301010 3
7001 30 3
2100 10 2
4000 31 6
xyu √ wP Constant
301 010 3
100
1
7
3
7
0
3
7
210010 2
400031 6
xyu √ wP Constant
001
3
7
2
7
0
1
7
2
100
1
7
3
7
0
3
7
010
2
7
1
7
0
2
7
0
000
4
7
9
7
1
5
7
4
xyu √ wP Constant
00
7
3
1
2
3
04
100
1
7
3
7
0
3
7
010
2
7
1
7
0
2
7
0
000
4
7
9
7
1
5
7
4
xyu√ wP Constant
00
7
3
1
2
3
04
10
1
3
0
1
3
01
01
2
3
0
1
3
04
00
4
3
0
5
3
110
Pivot
씮
row
앖
Pivot column
Ratio
2
1
2
9
3
3
5
1
5
Column 1 could have
been chosen as the
pivot column as
well.
Ratio
3
7
3
7
3
3
1
R
1
R
3
⎯⎯⎯→
R
2
3R
3
R
4
3R
3
Pivot
row
씮
앖
Pivot
column
R
1
3R
2
⎯⎯⎯→
R
3
2R
2
R
4
4R
2
Pivot
row
씮
앖
Pivot
column
Ratio
4
—
—
We now use the
simplex method for
problems in standard
form to complete the
problem.
R
1
⎯→
7
3
R
2
⎯⎯→
1
7
R
2
R
1
⎯⎯⎯→
R
3
R
1
R
4
R
1
4
7
2
7
1
7
y
x
(0, 2)
(1, 4)
S
3
7
20
7
–2x + y = 2
x + y = 5
x + 3y = 9
,
FIGURE 7
The feasible set S and the path leading
from the initial nonfeasible point
(0, 0) to the optimal point (1, 4)
87533_04_ch4_p201-256 1/30/08 9:52 AM Page 247

APPLIED EXAMPLE 5
Production Planning Rockford manufactures
two models of exercise bicycles—a standard model and a deluxe model—
in two separate plants, plant I and plant II. The maximum output at plant I is
1200 per month, and the maximum output at plant II is 1000 per month. The
profit per bike for standard and deluxe models manufactured at plant I is $40 and
$60, respectively; the profit per bike for standard and deluxe models manufac-
tured at plant II is $45 and $50, respectively.
For the month of May, Rockford received an order for 1000 standard models
and 800 deluxe models. If prior commitments dictate that the number of deluxe
models manufactured at plant I not exceed the number of standard models manu-
factured there by more than 200, find how many of each model should be pro-
duced at each plant so as to satisfy the order and at the same time maximize
Rockford’s profit.
Solution
Let x and y denote the number of standard and deluxe models to be
manufactured at plant I. Since the number of standard and deluxe models re-
quired are 1000 and 800, respectively, we see that the number of standard and
deluxe models to be manufactured at plant II are (1000 x) and (800 y),
respectively. Rockford’s profit will then be
P 40x 60y 45(1000 x) 50(800 y)
85,000 5x 10y
Since the maximum output of plant I is 1200, we have the constraint
x y 1200
Similarly, since the maximum output of plant II is 1000, we have
(1000 x) (800 y) 1000
or, equivalently,
x y 800
Finally, the additional constraints placed on the production schedule at plants I
and II translate into the inequalities
y x 200
x 1000
y 800
To summarize, the problem at hand is the following nonstandard problem:
Maximize P 85,000 5x 10y
subject to x y 1200
x y 800
x y 200
x 1000
y 800
x 0, y 000 0
Let’s introduce the slack variables, u, √, w, r, and s. Using the simplex method for
nonstandard problems, we obtain the following sequence of tableaus:
248 4 LINEAR PROGRAMMING: AN ALGEBRAIC APPROACH
87533_04_ch4_p201-256 1/30/08 9:52 AM Page 248
4.3 THE SIMPLEX METHOD: NONSTANDARD PROBLEMS 249
xyu√ wr s P Constant
1 1100000 1,200
1 1010000 800
1 1001000 200
1 0000100 1,000
0 1000010 800
5 10000001 85,000
xyu√ wr s P Constant
1 11 00000 1,200
11010000 800
1 10 01000 200
1 00 00100 1,000
0 10 00010 800
5 10 0 0 0 0 0 1 85,000
xyu√ wr s P Constant
0 01 10000 400
1101 0 0 0 0 800
0201 1 0 0 0 1,000
0 10 10100 200
0 10 00010 800
0 150 50001 81,000
xyu√ wr s P Constant
0 01 10000 400
1101 0 0 0 0 800
010
1
2
1
2
0 0 0 500
0 10 10100 200
0 10 00010 800
0 150 50001 81,000
xyu √ wrsP Constant
001 1 0000 400
100
1
2
1
2
0 0 0 300
010
1
2
1
2
0 0 0 500
000
1
2
1
2
100 700
000
1
2
1
2
010 300
000
5
2
1
2
5
0 0 1 88,500
Pivot
씮
row
앖
Pivot column
Ratio
—
—
1000
1
1000
800
1
800
1200
1
1200
R
2
⎯→
Ratio
—
—
800
1
800
1000
2
500
800
1
800
We now use the
simplex method
for standard
problems.
R
1
R
2
R
3
R
2
⎯⎯⎯→
R
4
R
2
R
6
5R
2
Pivot
row
씮
앖
Pivot column
앖
Pivot column
Ratio
—
—
300
1/2
600
700
1/2
1400
400
1
400
R
2
R
3
R
4
R
3
———
씮
R
5
R
3
R
6
15R
3
Pivot row 씮
R
3
⎯→
1
2
R
2
R
1
R
3
R
1
⎯⎯⎯→
R
4
R
1
R
5
R
1
R
6
R
1
5
2
1
2
1
2
1
2
1
2
xy u√ wrsP Constant
00 11 0000 400
10
1
2
0
1
2
0 0 0 500
01
1
2
0
1
2
000 700
00
1
2
0
1
2
100 500
00
1
2
0
1
2
010 100
00
5
2
0
1
2
5
0 0 1 89,500
87533_04_ch4_p201-256 1/30/08 9:52 AM Page 249

250 4 LINEAR PROGRAMMING: AN ALGEBRAIC APPROACH
All entries in the last row are nonnegative, and the tableau is final. We see that
x 500, y 700, and P 89,500. This tells us that plant I should manufacture
500 standard and 700 deluxe exercise bicycles and that plant II should manufac-
ture (1000 500), or 500, standard and (800 700), or 100, deluxe models.
Rockford’s profit will then be $89,500.
1. Solve the following nonstandard problem using the method
of this section:
Maximize P 2x 3y
subject to x y 40
x 2y 10
x 0, y 0
2. A farmer has 150 acres of land suitable for cultivating
crops A and B. The cost of cultivating crop A is $40/acre
and that of crop B is $60/acre. The farmer has a maximum
of $7400 available for land cultivation. Each acre of crop
A requires 20 labor-hours, and each acre of crop B requires
25 labor-hours. The farmer has a maximum of 3300 labor-
hours available. She has also decided that she will cultivate
at least 70 acres of crop A. If she expects to make a profit
of $150/acre on crop A and $200/acre on crop B, how
many acres of each crop should she plant in order to max-
imize her profit?
Solutions to Self-Check Exercises 4.3 can be found on
page 253.
1. Explain why the following linear programming problem is
not a standard maximization problem.
Maximize P 2x 3y
subject to 4x 2y 20
2x 3y 5
x 0, y 0
2. Explain why the following linear programming problem is
not a restricted standard minimization problem.
Minimize C 3x y
subject to x y 5
3x 5y 16
x 0, y 0
3. Explain why the following linear programming problem is
not a standard maximization problem.
Maximize P x 3y
subject to 3x 4y 16
2x 3y 5
x 0, y 0
Can it be rewritten as a restricted standard minimization
problem? Why or why not?
Explore & Discuss
Refer to Example 5.
1. Sketch the feasible set S for the linear programming problem.
2. Solve the problem using the method of corners.
3. Indicate on S the points (both nonfeasible and feasible) corresponding to each iteration of
the simplex method, and trace the path leading to the optimal solution.
4.3 Self-Check Exercises
4.3 Concept Questions
87533_04_ch4_p201-256 1/30/08 9:52 AM Page 250

4.3 THE SIMPLEX METHOD: NONSTANDARD PROBLEMS 251
4.3 Exercises
In Exercises 1–4, rewrite each linear programming prob-
lem as a maximization problem with constraints involv-
ing inequalities of the form ⱕ a constant (with the excep-
tion of the inequalities x ⱖ 0, y ⱖ 0, and z ⱖ 0).
1. Minimize C 2x 3y
subject to 3x 5y 20
3x y 16
2x y 1
x 0, y 0
2. Minimize C 2x 3y
subject to x y 10
x 2y 12
2x y 12
x 0, y 0
3. Minimize C 5x 10y z
subject to 2x y z 4
x 2y 2z 2
2x 4y
3z 12
x 0, y 0, z 0
4. Maximize P 2x y 2z
subject to x 2y z 10
3x 4y 2z 5
2x 5y 12z 20
x 0, y 0, z 0
In Exercises 5–20, use the method of this section to solve
each linear programming problem.
5. Maximize P x 2y
subject to 2 x 5y 20
x 5y 5
x 0, y 0
6. Maximize P 2x 3y
subject to x 2y 8
x y 2
x 0, y 0
7. Minimize C 2x y
subject to x 2y 6
3x 2y 12
x 0, y 0
8. Minimize C 2x 3y
subject to x 3y 60
2x
y 45
x 40
x 0, y 0
9. Maximize P x 4y
subject to x 3y 6
2x 3y 6
x 0, y 0
10. Maximize P 5x y
subject to 2x y 8
x y 2
x 0, y 0
11. Maximize P x 2y
subject to 2 x 3y 12
x 3y 3
x 0, y 0
12. Minimize C x
2y
subject to 4x 7y 70
2x y 20
x 0, y 0
13. Maximize P 5x 4y 2z
subject to x 2y 3z 24
x y z 6
x 0, y 0, z 0
14. Maximize P x 2y z
subject to 2x 3y 2z 12
x 2y 3z 6
x 0, y 0, z 0
15. Minimize C
x 2y z
subject to x 2y 3z 10
2x y 2z 15
2x y 3z 20
x 0, y 0, z 0
16. Minimize C 2x 3y 4z
subject to x 2y z 8
x 2y 2z 10
2x 4y 3z 12
x 0, y 0, z 0
87533_04_ch4_p201-256 1/30/08 9:52 AM Page 251
