Таран Т.А. Основы дискретной математики

Подождите немного. Документ загружается.

Òàðàí Ò. À.

Îñíîâû

äèñêðåòíîé

ìàòåìàòèêè

Êèåâ

«Ïðîñâ³òà»

2003

Òàðàí Ò. À.

Îñíîâû äèñêðåòíîé ìàòåìàòèêè. Ê.: Ïðîñâ³òà, 2003. 288ñ.

Àííîòàöèÿ àííîòàöèÿ àííîòàöèÿ àííîòàöèÿ àííîòàöèÿ

àííîòàöèÿ àííîòàöèÿ àííîòàöèÿ àííîòàöèÿ àííîòàöèÿ àííîòàöèÿ

àííîòàöèÿ àííîòàöèÿ àííîòàöèÿ àííîòàöèÿ àííîòàöèÿ.

Àííîòàöèÿ àííîòàöèÿ àííîòàöèÿ àííîòàöèÿ àííîòàöèÿ

àííîòàöèÿ àííîòàöèÿ àííîòàöèÿ.

Èë. 103. Òàáë. 25. Ñïèñîê ëèò.: ñ. 287 (48 íàçâ.)

Àííîòàö³ÿ àííîòàöèÿ àííîòàöèÿ àííîòàöèÿ àííîòàöèÿ

àííîòàöèÿ àííîòàöèÿ àííîòàöèÿ àííîòàöèÿ àííîòàöèÿ àííîòàöèÿ

àííîòàöèÿ àííîòàöèÿ àííîòàöèÿ.

Àííîòàö³ÿ àííîòàöèÿ àííîòàöèÿ àííîòàöèÿ àííîòàöèÿ

àííîòàöèÿ àííîòàöèÿ àííîòàöèÿ.

ÁÁÊ ????? ?????

Ò ??

ISBN-966-7115-

Ïðåäèñëîâèå

Äèñêðåòíàÿ ìàòåìàòèêà ÿâëÿåòñÿ áàçîâûì êóðñîì ïðè

ïîäãîòîâêå ñïåöèàëèñòîâ ïî èíôîðìàöèîííûì òåõíîëîãèÿì è

èñêóññòâåííîìó èíòåëëåêòó. Îäíàêî, íåñìîòðÿ íà òî, ÷òî

âû÷èñëèòåëüíàÿ òåõíèêà è ïðîãðàììèðîâàíèå ñóùåñòâóþò óæå

áîëåå ïÿòèäåñÿòè ëåò, äî ñèõ ïîð íåò òàêîãî ó÷åáíèêà, êîòîðûé

ñòàë áû «êëàññè÷åñêèì» äëÿ ýòîé äèñöèïëèíû. Ó÷åáíèêè ïî

äèñêðåòíîé ìàòåìàòèêå â çíà÷èòåëüíîé ñòåïåíè îòðàæàþò îáëàñòü

èíòåðåñîâ è ñèìïàòèè èõ àâòîðîâ. Ýòî âî ìíîãîì îáóñëîâëåíî

ðàçíîîáðàçèåì ìàòåðèàëà, êîòîðûé îòíîñÿò ê êóðñó «Äèñêðåòíàÿ

ìàòåìàòèêà». Ïðåäëàãàåìûé ó÷åáíèê íå ÿâëÿåòñÿ èñêëþ÷åíèåì â

ýòîì îòíîøåíèè. Êíèãà íàïèñàíà ïî ìàòåðèàëàì ëåêöèé, êîòîðûå

â òå÷åíèå íåñêîëüêèõ ëåò ÷èòàþòñÿ àâòîðîì â Íàöèîíàëüíîì

òåõíè÷åñêîì óíèâåðñèòåòå Óêðàèíû «Êèåâñêèé ïîëèòåõíè÷åñêèé

èíñòèòóò». Ýòî âòîðîå èçäàíèå ó÷åáíèêà, ïåðâîå èçäàíèå âûøëî â

1998 ã. â èçäàòåëüñòâå «Ïðîñâ³òà».

Öåëüþ ó÷åáíèêà ÿâëÿåòñÿ èçëîæåíèå îñíîâíûõ ïîíÿòèé è

ìåòîäîâ, íåîáõîäèìûõ äëÿ èçó÷åíèÿ ïîñëåäóþùèõ äèñöèïëèí

ñïåöèàëüíîñòåé «ïðèêëàäíàÿ ìàòåìàòèêà», «èíôîðìàöèîííûå

òåõíîëîãèè» è ïð., ôîðìèðîâàíèå ìèðîâîççðåíèÿ íà äèñêðåòíóþ

ìàòåìàòèêó è ëîãèêó êàê íà ôóíäàìåíòàëüíóþ íàóêó, èñïîëüçóåìóþ

äëÿ ôîðìàëèçàöèè çíàíèé. Ïîýòîìó â êíèãó âêëþ÷åíû îñíîâíûå

ðàçäåëû, èñïîëüçóåìûå â íîâûõ èíôîðìàöèîííûõ òåõíîëîãèÿõ,

òàêèõ êàê ñèñòåìû îáðàáîòêè äàííûõ, ìîäåëèðîâàíèå ñëîæíûõ

ñèñòåì, ñèñòåìû èñêóññòâåííîãî èíòåëëåêòà.

Êíèãà ñîñòîèò èç 15 ãëàâ. Óñëîâíî åå ìîæíî ðàçäåëèòü íà äâå

÷àñòè. Ïåðâàÿ ÷àñòü ñîäåðæèò òðàäèöèîííûå ðàçäåëû äèñêðåòíîé

ìàòåìàòèêè: òåîðèþ ìíîæåñòâ, òåîðèþ îòíîøåíèé è îòîáðàæåíèé,

îñíîâû òåîðèè ãðàôîâ. Â ïîñëåäíåå âðåìÿ â òåîðèè èñêóññòâåííîãî

èíòåëëåêòà âñå ÷àùå èñïîëüçóþòñÿ òàêèå ñòðóêòóðû, êàê ðåøåòêè,

ïîýòîìó â ó÷åáíèê âêëþ÷åíû îñíîâû òåîðèè ðåøåòîê è èõ ïðåäñòàâ-

ëåíèé. Âòîðàÿ ÷àñòü ó÷åáíèêà ïîñâÿùåíà ìàòåìàòè÷åñêîé ëîãèêå.

Ïðè èçëîæåíèè îñíîâ ìàòåìàòè÷åñêîé ëîãèêè îñíîâíîå âíèìà-

íèå óäåëÿåòñÿ ïðèìåíåíèþ ëîãè÷åñêèõ ìåòîäîâ äëÿ ôîðìàëèçàöèè

çíàíèé è ðàññóæäåíèé. Ïðè èçëîæåíèè ìàòåìàòè÷åñêîé ëîãèêè

âåäóùèìè ÿâëÿþòñÿ èäåè, ñâÿçàííûå ñ ïîíÿòèåì àêñèîìàòè÷åñêîãî

ìåòîäà, åãî èñïîëüçîâàíèåì äëÿ ïîñòðîåíèÿ ôîðìàëüíûõ ñèñòåì,

îòîáðàæåíèåì ôîðìàëüíîé ñèñòåìû íà ìîäåëè è ïðèìåíåíèåì ýòîãî

ìàòåìàòè÷åñêîãî àïïàðàòà äëÿ ôîðìàëèçàöèè è èññëåäîâàíèÿ

ïðîáëåìíûõ îáëàñòåé. Ïîýòîìó ïðè èçëîæåíèè ëîãèêè ïðèâîäèòñÿ

áîëüøîå êîëè÷åñòâî ñîäåðæàòåëüíûõ ëîãè÷åñêèõ çàäà÷.

Íåñìîòðÿ íà òî, ÷òî ó÷åáíèê ïðåäíàçíà÷åí äëÿ èíæåíåðîâ, â

êíèãó âêëþ÷åíû íåêîòîðûå äîâîëüíî àáñòðàêòíûå ðàçäåëû îñíî-

Ï³äï. äî äðóêó ??.??.2003. Ôîðìàò 84õ108/32. Ïàï³ð îôñ. Ñïîñ³á äðóêó  îôñåò.

Óì. äðóê. àðê. ??,??. Îáë.-âèä. àðê. ??,??. Çàì. ¹ . Íàêëàä ???? ïð.

Íàâ÷àëüíå âèäàííÿ

Òàðàí Òåòÿíà Àðõèï³âíà

Îñíîâè äèñêðåòíî¿ ìàòåìàòèêè

(Ðîñ³éñüêîþ ìîâîþ)

Â àâòîðñüê³é ðåäàêö³¿

Êîìïþòåðíà âåðñòêà Ì. ª. Ï³ãóðíîâ

Äèçàéí îáêëàäèíêè ?. ?. ?????????

Ðåöåíçåíòû: ?. ?. ?????????

?. ?. ?????????

4 Ïðåäèñëîâèå

Ãëàâà 1. ÌÍÎÆÅÑÒÂÀ

1.1. Ïîíÿòèå ìíîæåñòâà

Ñîçäàòåëåì òåîðèè ìíîæåñòâ áûë Ãåîðã Êàíòîð

. Îñíîâîé ýòîé

òåîðèè ÿâëÿåòñÿ ïîíÿòèå ìíîæåñòâà.

Îïðåäåëåíèå 1.1. (ïî Êàíòîðó) Ìíîæåñòâî S åñòü ëþáîå

ñîáðàíèå îïðåäåëåííûõ è ðàçëè÷èìûõ ìåæäó ñîáîé îáúåêòîâ

íàøåé èíòóèöèè èëè èíòåëëåêòà, ìûñëèìîå êàê åäèíîå öåëîå.

Ýòè îáúåêòû íàçûâàþòñÿ ýëåìåíòàìè ìíîæåñòâà.

Îïðåäåëåíèå Êàíòîðà íå ÿâëÿåòñÿ òî÷íûì ìàòåìàòè÷åñêèì

îïðåäåëåíèåì, ýòî èíòóèòèâíîå îïðåäåëåíèå ïîíÿòèÿ ìíîæåñòâà.

Â äàëüíåéøåì ìû óâèäèì, ÷òî òî÷íîå ìàòåìàòè÷åñêîå îïðåäåëå-

íèå ìíîæåñòâà âûçûâàåò ñåðüåçíûå çàòðóäíåíèÿ.

Ñóùåñòâåííûì ïóíêòîì êàíòîðîâñêîãî ïîíèìàíèÿ ìíîæåñòâà

ÿâëÿåòñÿ òî, ÷òî ñîáðàíèå îáúåêòîâ «ìûñëèòñÿ êàê åäèíîå öåëîå», ò.å.

ñàìî ðàññìàòðèâàåòñÿ êàê îäèí ïðåäìåò. Ñàìè æå «îáúåêòû íàøåé

èíòóèöèè èëè èíòåëëåêòà» ìîãóò áûòü ñîâåðøåííî ïðîèçâîëüíûìè:

ìíîæåñòâî ìîæåò ñîñòîÿòü, íàïðèìåð, èç ñòóäåíòîâ äàííîãî êóðñà,

çâåçä íà íåáå èëè ïðîñòûõ ÷èñåë, îïðåäåëåíèå íå íàêëàäûâàåò íèêàêèõ

îãðàíè÷åíèé íà ïðèðîäó ïðåäìåòîâ, âõîäÿùèõ â ìíîæåñòâî. Â

ìàòåìàòèêå â êà÷åñòâå ýëåìåíòîâ ìíîæåñòâ îáû÷íî âûñòóïàþò òàêèå

îáúåêòû, êàê òî÷êè, êðèâûå, ÷èñëà, ìíîæåñòâà ÷èñåë è ò. ï. Êàíòî-

ðîâñêàÿ ôîðìóëèðîâêà ïîçâîëÿåò òàêæå ðàññìàòðèâàòü ìíîæåñòâà,

ýëåìåíòû êîòîðûõ ïî òîé èëè èíîé ïðè÷èíå íåëüçÿ òî÷íî óêàçàòü.

Â êàíòîðîâñêîé êîíöåïöèè ìíîæåñòâà óêàçûâàåòñÿ, ÷òî ýëåìåí-

òû ìíîæåñòâà äîëæíû áûòü «ðàçëè÷èìûìè» îáúåêòàìè, ò.å. ìíîæå-

ñòâî íå ìîæåò ñîäåðæàòü äâóõ îäèíàêîâûõ ýëåìåíòîâ. Ýïèòåò «îïðå-

äåëåííûé» ïîíèìàåòñÿ â òîì ñìûñëå, ÷òî åñëè äàíî êàêîå-ëèáî

ìíîæåñòâî è íåêîòîðûé ïðåäìåò, òî ìîæíî îïðåäåëèòü, ÿâëÿåòñÿ

ýòîò ïðåäìåò ýëåìåíòîì äàííîãî ìíîæåñòâà èëè íåò. Îòñþäà âûòå-

êàåò, ÷òî ìíîæåñòâî ïîëíîñòüþ îïðåäåëÿåòñÿ ñâîèìè ýëåìåíòàìè.

Â äàëüíåéøåì áóäåì èñïîëüçîâàòü ñòàíäàðòíûå îáîçíà÷åíèÿ

÷èñëîâûõ ìíîæåñòâ: Nìíîæåñòâî íàòóðàëüíûõ ÷èñåë; Z

ìíîæåñòâî öåëûõ ÷èñåë; Q ìíîæåñòâî ðàöèîíàëüíûõ ÷èñåë; R

ìíîæåñòâî âåùåñòâåííûõ ÷èñåë; Cìíîæåñòâî êîìïëåêñíûõ ÷èñåë.

Îá ýëåìåíòàõ ãîâîðÿò, ÷òî îíè ïðèíàäëåæàò ìíîæåñòâó, è

çàïèñûâàþò ýòî òàê: x ∈ A (÷èòàåòñÿ: «x ïðèíàäëåæèò ìíîæåñòâó

A», èëè «x ÿâëÿåòñÿ ýëåìåíòîì ìíîæåñòâà A»). Äîïóñêàåòñÿ çàïèñü:

, x

, ..., x

∈A, åñëè âñå ýòè ýëåìåíòû ïðèíàäëåæàò ìíîæåñòâó A.

Çàïèñü x∉A îçíà÷àåò, ÷òî x íå ïðèíàäëåæèò ìíîæåñòâó A.

Ãåîðã Êàíòîð (Cantor) (18451918)  íåìåöêèé ìàòåìàòèê.

âàíèé ìàòåìàòèêè: èññëåäîâàíèå ñâîéñòâ èñ÷èñëåíèÿ ïðåäèêàòîâ,

ôîðìàëèçàöèÿ àðèôìåòèêè è òåîðåìà Ã¸äåëÿ î íåïîëíîòå. Çíà÷åíèå

òåîðåìû Ãåäåëÿ âûõîäèò çà ðàìêè ôîðìàëüíîé àðèôìåòèêè è èìååò

îáùåìàòåìàòè÷åñêèé õàðàêòåð. Ýòà òåîðåìà ãîâîðèò î íåâîçìîæ-

íîñòè ïîëíîé ôîðìàëèçàöèè ñêîëüêî-íèáóäü ñëîæíîé ìàòåìàòè÷åñ-

êîé òåîðèè è ÷àñòî èñïîëüçóåòñÿ ïðè îáñóæäåíèè ìåòîäîëîãè÷åñêèõ

ïðîáëåì ôîðìàëèçàöèè, ñðàâíèòåëüíûõ âîçìîæíîñòåé ÷åëîâåêà è

êîìïüþòåðà è ò.ä. Ïîýòîìó çíàêîìñòâî ñ òåîðåìîé Ãåäåëÿ ñëåäóåò

ñ÷èòàòü ýëåìåíòîì ìàòåìàòè÷åñêîé êóëüòóðû, íåîáõîäèìûì íå

òîëüêî äëÿ ïðîôåññèîíàëîâ-ìàòåìàòèêîâ,  ïîäîáíî òîìó, êàê çíà-

íèå î íåâîçìîæíîñòè âå÷íîãî äâèãàòåëÿ íåîáõîäèìî íå òîëüêî äëÿ

ïðîôåññèîíàëîâ-ôèçèêîâ.

Ïîñëåäíÿÿ ãëàâà ïîñâÿùåíà èçëîæåíèþ îñíîâ òåîðèè àëãîðèò-

ìîâ. Îñíîâíîå âíèìàíèå óäåëÿåòñÿ èçó÷åíèþ ïðîáëåìû âû÷èñëè-

ìîñòè è ñâÿçè åå ñ ïðîáëåìàìè ëîãè÷åñêîãî âûâîäà.

Ìíîãèå ðàçäåëû, òàêèå, êàê «Êîìáèíàòîðèêà», «Àáñòðàêòíûå

àëãåáðû», «Òåîðèÿ àâòîìàòîâ», íå âîøëè â äàííîå èçäàíèå. Â îñíîâ-

íîì ýòî îáúÿñíÿåòñÿ òåì, ÷òî îíè ÷èòàþòñÿ â äðóãèõ êóðñàõ, à

òàêæå îãðàíè÷åííîñòüþ îáúåìà êíèãè.

Àâòîð âûðàæàåò áëàãîäàðíîñòü Î. Ï. Êóçíåöîâó çà ñîâìåñòíóþ

ðàáîòó íàä ãëàâîé «Òåîðèÿ ãðàôîâ», à òàêæå çà öåííûå çàìå÷àíèÿ,

âûñêàçàííûå èì ïðè ÷òåíèè ðóêîïèñè. Àâòîð òàêæå ãëóáîêî áëàãî-

äàðåí Ñ. Â. Ñèðîòå, ãëàâíîìó ðåäàêòîðó èçäàòåëüñòâà «Ïðîñâ³òà»,

áåç êîòîðîãî ýòà êíèãà íå áûëà áû èçäàíà, è Ì. Å. Ïèãóðíîâó,

âçÿâøåìó íà ñåáÿ òðóä ïî ïîäãîòîâêå ìàêåòà êíèãè, à òàêæå ñâîèì

ðåöåíçåíòàì ....

6 7ÌíîæåñòâàÃëàâà 1

Îäíîçíà÷íî îïðåäåëåííîå ìíîæåñòâî X, ýëåìåíòàìè êîòîðîãî

ÿâëÿþòñÿ ïðåäìåòû x

, x

, ..., x

, áóäåì îáîçíà÷àòü X={x

, x

, ..., x

Â ÷àñòíîñòè, {x}  òàê íàçûâàåìîå åäèíè÷íîå ìíîæåñòâî,  åñòü

îäíîýëåìåíòíîå ìíîæåñòâî, åäèíñòâåííûì ýëåìåíòîì êîòîðîãî

ÿâëÿåòñÿ x. Åñëè ìíîæåñòâî X êîíå÷íîå, òî êîëè÷åñòâî ýëåìåíòîâ

â ìíîæåñòâå îáîçíà÷àåòñÿ |X|. Íàïðèìåð, åñëè X={a, b, c}, òî |X|=3.

Ïîðÿäîê ñëåäîâàíèÿ ýëåìåíòîâ â ìíîæåñòâå íå èìååò çíà÷åíèÿ.

Íàïðèìåð, {a, b, c} è {c, a, b}  ýòî îäíî è òî æå ìíîæåñòâî.

Ýëåìåíòû êàêîãî-ëèáî ìíîæåñòâà ñàìè ìîãóò áûòü ìíî-

æåñòâàìè. Íàïðèìåð, ìíîæåñòâî A={{1, 3}, {2, 4}, {5, 6}} åñòü

ìíîæåñòâî èç òðåõ ýëåìåíòîâ (|A|=3), à èìåííî: {1, 3}, {2, 4} è

{5,6}. Ìíîæåñòâà B={{1, 2}, {2, 3}} è C={1, 2, 3}  ðàçëè÷íûå

ìíîæåñòâà, òàê êàê ýëåìåíòàìè ïåðâîãî ÿâëÿþòñÿ {1, 2}, {2, 3}, è

|B|= 2, à ýëåìåíòàìè âòîðîãî1, 2 è 3, |C| = 3. Ìíîæåñòâà D={{1,2}}

è G={1,2} òàêæå ðàçëè÷íû, òàê êàê ïåðâîå  îäíîýëåìåíòíîå

ìíîæåñòâî, èìåþùåå åäèíñòâåííûì ñâîèì ýëåìåíòîì {1, 2}, à âòîðîå

èìååò ñâîèìè ýëåìåíòàìè 1 è 2.

Íà îñíîâàíèè êàíòîðîâñêîãî ïîíèìàíèÿ ìíîæåñòâà ìîæíî äàòü

îïðåäåëåíèå ìíîæåñòâà ÷åðåç åãî ñâîéñòâà, êîòîðûå ïîñòóëèðóþòñÿ

êàê èíòóèòèâíûå ïðèíöèïû.

1.1.1. Èíòóèòèâíûé ïðèíöèï îáúåìíîñòè

Èíòóèòèâíûé ïðèíöèï îáúåìíîñòè ôîðìóëèðóåòñÿ ñëåäóþùèì

îáðàçîì.

Äâà ìíîæåñòâà ðàâíû òîãäà è òîëüêî òîãäà, êîãäà îíè ñîñòîÿò

èç îäíèõ è òåõ æå ýëåìåíòîâ.

Ðàâåíñòâî ìíîæåñòâ îáîçíà÷àåòñÿ: A=B, íåðàâåíñòâî  A≠B.

Äîêàçàòåëüñòâî ðàâåíñòâà êàêèõ-ëèáî äâóõ êîíêðåòíûõ

ìíîæåñòâ A è B ñîñòîèò èç äâóõ ÷àñòåé: íåîáõîäèìî äîêàçàòü, ÷òî

åñëè x∈A, òî x∈B, è îáðàòíîå: åñëè x∈B, òî x∈A.

Ïðèìåð 1. Äîêàæåì, ÷òî ìíîæåñòâî A âñåõ ÷åòíûõ ïîëîæè-

òåëüíûõ öåëûõ ÷èñåë ðàâíî ìíîæåñòâó B ïîëîæèòåëüíûõ öåëûõ

÷èñåë, ïðåäñòàâèìûõ â âèäå ñóììû äâóõ íå÷åòíûõ ïîëîæèòåëüíûõ

öåëûõ ÷èñåë.

Äîïóñòèì ñíà÷àëà, ÷òî x∈A, è äîêàæåì, ÷òî x∈B. Äåéñòâèòåëü-

íî, åñëè x∈A, òî x=2m, òàê ÷òî x=(2m1)+1. Ýòî è îçíà÷àåò,

÷òî x∈B.

Ïðåäïîëîæèì òåïåðü, ÷òî x∈B, è âûâåäåì îòñþäà, ÷òî x∈A.

Åñëè x∈B, òî x=(2p1)+(2q1), îòêóäà x=2(p+q1), èç

÷åãî ñëåäóåò, ÷òî x∈A.

Òàêèì îáðàçîì, ìû äîêàçàëè, ÷òî ìíîæåñòâà A è B ñîñòîÿò èç

îäíèõ è òåõ æå ýëåìåíòîâ, ñëåäîâàòåëüíî, A=B.

1.1.2. Èíòóèòèâíûé ïðèíöèï àáñòðàêöèè

Îáîçíà÷åíèå ìíîæåñòâà ñ ïîìîùüþ ïåðå÷èñëåíèÿ åãî ýëåìåíòîâ

ñëèøêîì ãðîìîçäêî, ÷òîáû åãî èñïîëüçîâàòü äëÿ çàäàíèÿ ìíîæåñòâ,

èìåþùèõ, õîòÿ è êîíå÷íîå, íî áîëüøîå ÷èñëî ýëåìåíòîâ, è âîâñå

íåïðèìåíèìî äëÿ áåñêîíå÷íûõ ìíîæåñòâ.

Îïðåäåëåíèå 1.2. Áóäåì ïîíèìàòü ïîä âûñêàçûâàíèåì ïîâåñòâî-

âàòåëüíîå ïðåäëîæåíèå, êîòîðîå ìîæíî îõàðàêòåðèçîâàòü êàê

èñòèííîå èëè ëîæíîå. Òîãäà ïîä îäíîìåñòíûì ïðåäèêàòîì

(ôîðìîé) îò x  P(x) áóäåì ïîíèìàòü êîíå÷íóþ ïîñëåäîâàòåëü-

íîñòü, ñîñòîÿùóþ èç ñëîâ è ñèìâîëà x, òàêóþ, ÷òî åñëè êàæäîå

âõîæäåíèå x â ýòó ïîñëåäîâàòåëüíîñòü çàìåíèòü îäíèì è òåì

æå èìåíåì íåêîòîðîãî ïðåäìåòà ñîîòâåòñòâóþùåãî ðîäà, òî â

ðåçóëüòàòå ïîëó÷èòñÿ âûñêàçûâàíèå. Íàïðèìåð, êàæäîå èç

ñëåäóþùèõ âûðàæåíèé åñòü ïðåäèêàò îò x:

5 äåëèò x; õ

+x+1 > 0; x ëþáèò Äæîíà; õ

=2; 0 < x.

Òåïåðü ìîæíî ñôîðìóëèðîâàòü èíòóèòèâíûé ïðèíöèï

àáñòðàêöèè.

Ëþáîé îäíîìåñòíûé ïðåäèêàò P(x) îïðåäåëÿåò íåêîòîðîå

ìíîæåñòâî A òàêèì îáðàçîì, ÷òî ýëåìåíòàìè ìíîæåñòâà A ÿâëÿþò-

ñÿ òå è òîëüêî òå ïðåäìåòû à, äëÿ êîòîðûõ P(a) åñòü èñòèííîå

âûñêàçûâàíèå.

Ïîñêîëüêó ìíîæåñòâà, ñîñòîÿùèå èç îäíèõ è òåõ æå ýëåìåíòîâ,

ðàâíû, òî ëþáîé ïðåäèêàò P(x) îïðåäåëÿåò â òî÷íîñòè îäíî, âïîëíå

îïðåäåëåííîå, ìíîæåñòâî, îáû÷íî îáîçíà÷àåìîå â ìàòåìàòèêå ÷åðåç

{x | P(x)}, ÷òî ÷èòàåòñÿ òàê: «ìíîæåñòâî âñåõ òàêèõ x, ÷òî P(x)».

Òàêèì îáðàçîì, a∈ {x | P(x)} â òîì è òîëüêî òîì ñëó÷àå, åñëè P(a)

èñòèííîå âûñêàçûâàíèå. Ìîæíî ñêàçàòü, ÷òî ðåøåíèå âîïðîñà, ÿâëÿ-

åòñÿ ëè äàííûé ïðåäìåò a ýëåìåíòîì ìíîæåñòâà {x | P(x)}, åñòü

ðåøåíèå âîïðîñà, îáëàäàåò ëè a íåêîòîðûì îïðåäåëåííûì ñâîéñòâîì

(êà÷åñòâîì). Ïîýòîìó, êîãäà äëÿ îïðåäåëåíèÿ íåêîòîðîãî ìíîæåñòâà

A èñïîëüçóþò êàêîé-íèáóäü ïðåäèêàò P(x), åãî îáû÷íî íàçûâàþò

îïðåäåëÿþùèì ñâîéñòâîì ìíîæåñòâà A. Â òàêîì ñëó÷àå ïðèíöèï

àáñòðàêöèè ìîæíî ñôîðìóëèðîâàòü â âèäå óòâåðæäåíèÿ: «Êàæäîå

ñâîéñòâî îïðåäåëÿåò íåêîòîðîå ìíîæåñòâî».

Ââåäåíèå â îáðàùåíèå áåñêîíå÷íûõ ìíîæåñòâ ñ ïîìîùüþ

îïðåäåëÿþùèõ èõ ñâîéñòâ  ïðîöåäóðà, õîðîøî èçâåñòíàÿ èç

àíàëèòè÷åñêîé ãåîìåòðèè. Íàïðèìåð, îêðóæíîñòü ðàäèóñà 2 íà

ïëîñêîñòè ñ öåíòðîì â íà÷àëå êîîðäèíàò åñòü ìíîæåñòâî âñåõ òàêèõ

x, ÷òî x íàõîäèòñÿ íà ðàññòîÿíèè â äâå åäèíèöû îò íà÷àëà êîîðäèíàò.

Ñëåäóþùèå âûðàæåíèÿ ïðåäñòàâëÿþò ñîáîé ìíîæåñòâà,

îïðåäåëåííûå ïîñðåäñòâîì íåêîòîðûõ ñâîéñòâ:

A ={x | x ∈ N, x < 10} = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9};

8 9ÌíîæåñòâàÃëàâà 1

B ={x | x åñòü ôóíêöèÿ, íåïðåðûâíàÿ íà çàìêíóòîì îòðåçêå

äåéñòâèòåëüíûõ ÷èñåë îò 0 äî 1}.

Äëÿ îáîçíà÷åíèÿ ìíîæåñòâ èñïîëüçóþòñÿ è ðàçëè÷íûå âèäîèç-

ìåíåíèÿ îñíîâíîé ñêîáî÷íîé çàïèñè. Íàïðèìåð, C={x∈R | 0≤x≤1}

îáîçíà÷àåò ìíîæåñòâî âñåõ äåéñòâèòåëüíûõ ÷èñåë, ëåæàùèõ â

èíòåðâàëå [0,1], à D={x∈Q

| x

< 2}  ìíîæåñòâî âñåõ ïîëîæè-

òåëüíûõ ðàöèîíàëüíûõ ÷èñåë, êâàäðàòû êîòîðûõ ìåíüøå ÷èñëà 2.

Âìåñòî òîãî ÷òîáû ïèñàòü {y | y=2x, ãäå x åñòü öåëîå ÷èñëî}, ìû

ìîæåì íàïèñàòü {2x | x∈Z}. Àíàëîãè÷íî ÷åðåç {x

| x∈Z}

îáîçíà÷àåòñÿ ìíîæåñòâî êâàäðàòîâ öåëûõ ÷èñåë.

Ïðèíöèï îáúåìíîñòè, ïðèíöèï àáñòðàêöèè è ïðèíöèï âûáîðà

(ïîêà, çà íåíàäîáíîñòüþ, íå ñôîðìóëèðîâàííûé)  ýòî òà îñíîâà,

íà êîòîðîé ñòðîèòñÿ êàíòîðîâñêàÿ òåîðèÿ ìíîæåñòâ. Îñíîâíîå

ïîíÿòèå, èñïîëüçóåìîå ïðè ôîðìóëèðîâêå ýòèõ ïðèíöèïîâ, ýòî

ïðèíàäëåæíîñòü ýëåìåíòà ìíîæåñòâó.

1.1.3. Îòíîøåíèå âêëþ÷åíèÿ

Ââåäåì åùå äâà îòíîøåíèÿ ìåæäó ìíîæåñòâàìè.

Îïðåäåëåíèå 1.3. Åñëè A è B åñòü ìíîæåñòâà, òî ãîâîðÿò, ÷òî A

âêëþ÷åíî â B, åñëè êàæäûé ýëåìåíò ìíîæåñòâà A ÿâëÿåòñÿ òàêæå

ýëåìåíòîì ìíîæåñòâà B (ñèìâîëè÷åñêàÿ çàïèñü: A ⊆ B èëè

B⊇A). Â ýòîì ñëó÷àå ãîâîðÿò òàêæå, ÷òî ìíîæåñòâî A åñòü

ïîäìíîæåñòâî ìíîæåñòâà B.

Òàêèì îáðàçîì, A ⊆ B îçíà÷àåò, ÷òî äëÿ êàæäîãî x, åñëè x ∈ A,

òî x ∈ B.

Ìíîæåñòâî A ñòðîãî âêëþ÷åíî â B, èëè B ñòðîãî âêëþ÷àåò A,

èëè A åñòü ñîáñòâåííîå ïîäìíîæåñòâî B, åñëè A ⊆ B è A ≠ B

(ñèìâîëè÷åñêè: A ⊂ B).

Íàïðèìåð, ìíîæåñòâî ÷åòíûõ ÷èñåë ñòðîãî âêëþ÷åíî â

ìíîæåñòâî Z öåëûõ ÷èñåë, à ìíîæåñòâî Q ðàöèîíàëüíûõ ÷èñåë

ñòðîãî âêëþ÷àåò Z.

Îñíîâíûå ñâîéñòâà îòíîøåíèÿ âêëþ÷åíèÿ:

• X ⊆ X ðåôëåêñèâíîñòü,

• X ⊆ Y è Y ⊆ Z âëå÷åò X ⊆ Z òðàíçèòèâíîñòü,

• X ⊆ Y è Y ⊆ X âëå÷åò X=Y àíòèñèììåòðè÷íîñòü.

Ïîñëåäíåå ñâîéñòâî âûðàæàåò â òåðìèíàõ îòíîøåíèÿ âêëþ÷åíèÿ

äâà øàãà â äîêàçàòåëüñòâå ðàâåíñòâà äâóõ ìíîæåñòâ: äëÿ òîãî, ÷òîáû

äîêàçàòü, ÷òî X=Y, íàäî äîêàçàòü, ÷òî X ⊆ Y, à çàòåì, ÷òî Y ⊆ X.

Èç ïðèíöèïà îáúåìíîñòè ñëåäóåò, ÷òî ìîæåò áûòü òîëüêî îäíî

ìíîæåñòâî, íå èìåþùåå ýëåìåíòîâ. Ýòî ìíîæåñòâî íàçûâàþò

ïóñòûì ìíîæåñòâîì è îáîçíà÷àþò åãî ñèìâîëîì ∅. Ïóñòîå ìíîæå-

ñòâî åñòü ïîäìíîæåñòâî ëþáîãî ìíîæåñòâà.

Êàæäîå ìíîæåñòâî A≠∅ èìååò, ïî êðàéíåé ìåðå, äâà ðàçëè÷íûõ

ïîäìíîæåñòâà: ñàìî A è ∅, ò.å. A ⊆ A è ∅⊆A. Êðîìå òîãî, êàæäûé

ýëåìåíò ìíîæåñòâà A îïðåäåëÿåò íåêîòîðîå ïîäìíîæåñòâî

ìíîæåñòâà A: åñëè a∈A, òî {à} ⊆ A. Ïîäìíîæåñòâàìè ìíîæåñòâà

A áóäóò òàêæå ìíîæåñòâà, ñîñòàâëåííûå èç äâóõ ýëåìåíòîâ

ìíîæåñòâà A, òðåõ ýëåìåíòîâ, è òàê äàëåå. Â ðåçóëüòàòå ìû ïîëó÷èì

ìíîæåñòâî âñåõ ïîäìíîæåñòâ ìíîæåñòâà A.

Îïðåäåëåíèå 1.4. Ìíîæåñòâî âñåõ ïîäìíîæåñòâ ìíîæåñòâà A

íàçûâàåòñÿ ìíîæåñòâîì-ñòåïåíüþ ìíîæåñòâà A è îáîçíà÷àåòñÿ

℘(A).

Íàïðèìåð, åñëè A={1, 2, 3}, òî ℘(A)={{1, 2, 3}, {1, 2}, {1, 3},

{2, 3}, {1}, {2}, {3}, ∅}.

Ïîä÷åðêíåì ðàçëè÷èå ìåæäó îòíîøåíèÿìè ïðèíàäëåæíîñòè è

âêëþ÷åíèÿ: åñëè B ⊆ A, òî B ∈ ℘(A), à åñëè à ∈ A, òî {a} ⊆ A è

{a}∈ ℘(A).

Òåðìèí «ìíîæåñòâî-ñòåïåíü ìíîæåñòâà A» ïðèíÿò â êà÷åñòâå

íàèìåíîâàíèÿ ìíîæåñòâà âñåõ ïîäìíîæåñòâ ìíîæåñòâà A îòòîãî,

÷òî äëÿ êîíå÷íîãî ìíîæåñòâà A, ñîñòîÿùåãî èç n ýëåìåíòîâ, ℘(A)

èìååò 2

ýëåìåíòîâ.

Äîêàæåì ýòî óòâåðæäåíèå.

Áóäåì îáîçíà÷àòü C

êîëè÷åñòâî âñåâîçìîæíûõ ïåðåñòàíîâîê

èç n ïî k, îïðåäåëÿåìîå ôîðìóëîé:

)!(!

knk

−

. Â êîíå÷íîì ìíîæå-

ñòâå À, ñîñòîÿùåì èç n ýëåìåíòîâ, ñîäåðæàòñÿ: ïóñòîå ïîäìíîæåñòâî

∅, Ñ

îäíîýëåìåíòíûõ ïîäìíîæåñòâ, Ñ

äâóõýëåìåíòíûõ

ïîäìíîæåñòâ, ... , Ñ

k- ýëåìåíòíûõ ïîäìíîæåñòâ, ... , 1=Ñ



ñàìî ìíîæåñòâî À. Èòîãî: C

+C

+...+C

...+C

=

=(1+1)

= 2

ïîäìíîæåñòâ.

1.2. Îïåðàöèè íàä ìíîæåñòâàìè

Ïðîäîëæàÿ îïèñàíèå ìåòîäîâ ïîëó÷åíèÿ íîâûõ ìíîæåñòâ èç

óæå ñóùåñòâóþùèõ, ìû ââåäåì äâå îïåðàöèè, ïðè ïîìîùè êîòîðûõ

èç äâóõ ìíîæåñòâ ñòðîèòñÿ íîâîå ìíîæåñòâî.

Îïðåäåëåíèå 1.5. Îáúåäèíåíèå ìíîæåñòâ A è B (îáîçíà÷àåòñÿ

÷åðåç A∪B è ÷èòàåòñÿ êàê «îáúåäèíåíèå A è B») åñòü ìíîæåñòâî

âñåõ ïðåäìåòîâ, êîòîðûå ÿâëÿþòñÿ ýëåìåíòàìè ìíîæåñòâà A èëè

B, ò.å. A ∪ B={x | x ∈ A èëè x ∈ B}.

Çäåñü ïîäðàçóìåâàåòñÿ íå èñêëþ÷àþùèé ñìûñë ñëîâà «èëè».

Òàêèì îáðàçîì, ïî îïðåäåëåíèþ, x∈A ∪ B òîãäà è òîëüêî òîãäà,

êîãäà x åñòü ýëåìåíò õîòÿ áû îäíîãî èç ìíîæåñòâ A è B.

Íàïðèìåð: {1, 2, 3} ∪ {1, 3, 4}={1, 2, 3, 4}.

10 11

Îïðåäåëåíèå 1.6. Ïåðåñå÷åíèå ìíîæåñòâ A è B (îáîçíà÷àåòñÿ

÷åðåç A∩B è ÷èòàåòñÿ êàê «ïåðåñå÷åíèå A è B») åñòü ìíîæåñòâî

âñåõ ïðåäìåòîâ, êîòîðûå ÿâëÿþòñÿ ýëåìåíòàìè îáîèõ ìíîæåñòâ

A è B, ò.å. A∩B={x | x ∈ A è x ∈ B}.

Òàêèì îáðàçîì, ïî îïðåäåëåíèþ, x ∈ A ∩ B òîãäà è òîëüêî òîãäà,

êîãäà x ÿâëÿåòñÿ îäíîâðåìåííî ýëåìåíòîì ìíîæåñòâà A è ýëåìåíòîì

ìíîæåñòâà B.

Íàïðèìåð: {1, 2, 3} ∩ {1, 3, 4}={1, 3}.

Äëÿ âñÿêîé ïàðû ìíîæåñòâ A è B èìåþò ìåñòî ñëåäóþùèå

âêëþ÷åíèÿ:

∅ ⊆ A ∩ B ⊆ A ⊆ A ∪ B.

Îïðåäåëåíèå 1.7. Äâà ìíîæåñòâà A è B íàçûâàþòñÿ íåïåðåñåêàþùè-

ìèñÿ (èëè äèçúþíêòíûìè), åñëè A∩B=∅, è ïåðåñåêàþùèìèñÿ,

åñëè A∩B ≠ ∅. Ñèñòåìà ìíîæåñòâ íàçûâàåòñÿ ðàñ÷ëåíåííîé, åñëè

ëþáàÿ ïàðà åå ðàçëè÷íûõ ýëåìåíòîâ ÿâëÿåòñÿ íåïåðåñåêàþùåéñÿ.

Îïðåäåëåíèå 1.8. Ðàçáèåíèåì ìíîæåñòâà Õ áóäåì íàçûâàòü

òàêóþ ðàñ÷ëåíåííóþ ñèñòåìó U íåïóñòûõ è ðàçëè÷íûõ

ïîäìíîæåñòâ ìíîæåñòâà Õ, ãäå êàæäûé ýëåìåíò ìíîæåñòâà Õ

ÿâëÿåòñÿ â òî æå âðåìÿ ýëåìåíòîì íåêîòîðîãî (ñëåäîâàòåëüíî,

â òî÷íîñòè îäíîãî) ýëåìåíòà ñèñòåìû U.

Íàïðèìåð, {{1, 2}, {3}, {4, 5}} åñòü ðàçáèåíèå ìíîæåñòâà {1, 2, 3, 4, 5}.

Îïðåäåëåíèå 1.9. Àáñîëþòíîå äîïîëíåíèå ìíîæåñòâà A

(îáîçíà÷àåòñÿ ÷åðåç A′ èëè ¬A)  ýòî ìíîæåñòâî âñåõ ýëåìåíòîâ,

íå ÿâëÿþùèõñÿ ýëåìåíòàìè ìíîæåñòâà A: {x | x∉ A}.

Îïðåäåëåíèå 1.10. Îòíîñèòåëüíîå äîïîëíåíèå ìíîæåñòâà B äî

ìíîæåñòâà A  ýòî ìíîæåñòâî A∩B′; îíî îáû÷íî îáîçíà÷àåòñÿ

÷åðåç A\B (èíîãäà AB), ÷òî ÷èòàåòñÿ êàê «A ìèíóñ B».

Òàêèì îáðàçîì A\B = A∩B′ åñòü ñîêðàùåíèå äëÿ {x ∈ A | x∉B},

ò.å. ýòî ìíîæåñòâî òåõ ýëåìåíòîâ ìíîæåñòâà A, êîòîðûå íå ÿâëÿþòñÿ

ýëåìåíòàìè ìíîæåñòâà B.

Îïðåäåëåíèå 1.11. Ñèììåòðè÷åñêàÿ ðàçíîñòü ìíîæåñòâ A è B,

îáîçíà÷àåìàÿ ÷åðåç À÷B (èíîãäà èñïîëüçóþòñÿ îáîçíà÷åíèÿ

A∆B èëè A+B), îïðåäåëÿåòñÿ ñëåäóþùèì îáðàçîì: x∈A÷B

òîãäà è òîëüêî òîãäà, êîãäà x ïðèíàäëåæèò ðîâíî îäíîìó èç

ìíîæåñòâ À è Â:

A÷B = {x |(x ∈ A è x ∉ B) èëè (x ∉ A è x ∈ B)}.

Èç îïðåäåëåíèÿ ñëåäóåò, ÷òî A÷B=(A\B) ∪ (B\A).

Íåòðóäíî ïîêàçàòü, ÷òî ýòà îïåðàöèÿ êîììóòàòèâíà: A÷B=B÷A,

àññîöèàòèâíà: (A÷B)÷C=A÷(B÷C) è äèñòðèáóòèâíà

îòíîñèòåëüíî ïåðåñå÷åíèÿ: (A÷B)∩C=(A∩C)÷(B∩C). Êðîìå

òîãî, A÷A=∅ è A÷∅=A.

Åñëè âñå ðàññìàòðèâàåìûå â õîäå êàêîãî-ëèáî ðàññóæäåíèÿ ìíî-

æåñòâà ÿâëÿþòñÿ ïîäìíîæåñòâàìè íåêîòîðîãî ìíîæåñòâà U, òî ýòî

ìíîæåñòâî U íàçûâàþò óíèâåðñàëüíûì ìíîæåñòâîì (äëÿ ýòîãî ðàñ-

ñóæäåíèÿ). Íàïðèìåð, äëÿ ýëåìåíòàðíîé àðèôìåòèêè óíèâåðñàëü-

íûì ìíîæåñòâîì ñëóæèò Z, à äëÿ àíàëèòè÷åñêîé ãåîìåòðèè ïëîñ-

êîñòè  ìíîæåñòâî âñåõ óïîðÿäî÷åííûõ ïàð äåéñòâèòåëüíûõ ÷èñåë.

Äëÿ ãðàôè÷åñêîé èëëþñòðàöèè îòíîøåíèé, êîòîðûå ìîãóò èìåòü

ìåñòî ìåæäó ïîäìíîæåñòâàìè êàêîãî-ëèáî óíèâåðñàëüíîãî

ìíîæåñòâà U, ÷àñòî èñïîëüçóþò òàê íàçûâàåìûå äèàãðàììû Âåííà

ïî èìåíè àíãëèéñêîãî ñâÿùåííèêà Äæîíà Âåííà (18341923)

ïðèìåíÿâøåãî èõ â ñâîèõ èññëåäîâàíèÿõ ïî ëîãèêå. Äèàãðàììà

Âåííà ïðåäñòàâëÿåò ñîáîé ñõåìàòè÷åñêîå èçîáðàæåíèå ìíîæåñòâ â

âèäå òî÷å÷íûõ ìíîæåñòâ: óíèâåðñàëüíîå ìíîæåñòâî U èçîáðàæàåòñÿ

ìíîæåñòâîì òî÷åê íåêîòîðîãî ïðÿìîóãîëüíèêà, à åãî ïîäìíîæåñòâî

A  â âèäå êðóãà èëè êàêîé-íèáóäü äðóãîé ïðîñòîé îáëàñòè âíóòðè

ýòîãî ïðÿìîóãîëüíèêà. Ïðàâèëüíåå, îäíàêî, áûëî áû íàçâàòü èõ

äèàãðàììàìè Ýéëåðà, ïîñêîëüêó çàäîëãî äî Âåííà èõ óïîòðåáëÿë

çíàìåíèòûé øâåéöàðñêèé ìàòåìàòèê Ëåîíàðä Ýéëåð (17071783)

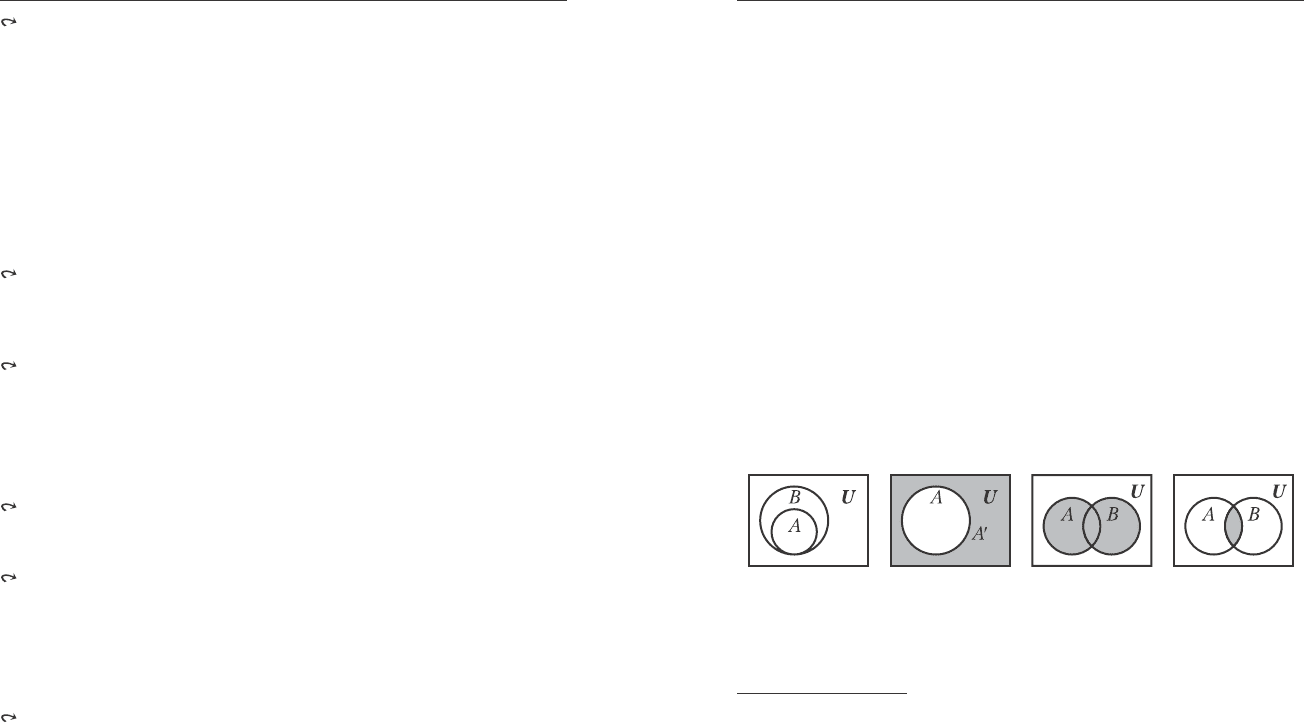
Íèæå íà ðèñ. 1.1. ïîêàçàíû îñíîâíûå îïåðàöèè íàä ìíîæåñòâàìè.

Ðèñ. 1.1. Äèàãðàììû Âåííà è êðóãè Ýéëåðà.

ÌíîæåñòâàÃëàâà 1

Âïðî÷åì, ñòàâ äîêòîðîì íàóê è, áóäó÷è èçáðàí â Àêàäåìèþ  àíãëèéñêîå

Êîðîëåâñêîå îáùåñòâî, Âåíí ïîëíîñòüþ îòêàçàëñÿ îò öåðêîâíîé äåÿòåëüíîñòè â

ïîëüçó çàíÿòèé ìàòåìàòè÷åñêîé ëîãèêîé è äàæå îôîðìèë ïèñüìåííûé äîêóìåíò,

óäîñòîâåðÿþùèé åãî íåñïîñîáíîñòü ê èñïîëíåíèþ îáÿçàííîñòåé ñâÿùåííèêà.

Â «Ïèñüìàõ íåìåöêîé ïðèíöåññå» (1768) Ë. Ýéëåð, îáúÿñíÿÿ ñâîåé êîððåñ-

ïîíäåíòêå ïðîñòîòó àðèñòîòåëåâîé ñèëëîãèñòèêè, ñèñòåìàòè÷åñêè èçîáðàæàë

îòäåëüíûå ìíîæåñòâà îáúåêòîâ êðóãàìè íà ïëîñêîñòè. Ñîîòâåòñòâóþùèå

äèàãðàììû, ìàëî îòëè÷àþùèåñÿ îò äèàãðàìì Âåííà, ÷àñòî íàçûâàþò êðóãàìè

Ýéëåðà. Âïðî÷åì, ïîäîáíûå ãðàôè÷åñêèå èëëþñòðàöèè òåîðåòèêî-

ìíîæåñòâåííûõ è ëîãè÷åñêèõ çàâèñèìîñòåé âñòðå÷àëèñü è äî Ýéëåðà, íàïðèìåð

â âåñüìà ïðèìå÷àòåëüíûõ, íî, ê ñîæàëåíèþ, îñòàâøèõñÿ íåîïóáëèêîâàííûìè

çàìåòêàõ ïî ëîãèêå Ãîòôðèäà Âèëüãåëüìà Ëåéáíèöà (16461716).

Îòíîøåíèå

âêëþ÷åíèÿ:

A ⊆ B, A∩B=A.

Àáñîëþòíîå

äîïîëíåíèå: A′.

Îáúåäèíåíèå

ìíîæåñòâ

A∪B.

Ïåðåñå÷åíèå

ìíîæåñòâ

A∩B.

12 13

1.3. Àëãåáðà ìíîæåñòâ

1.3.1. Îïðåäåëåíèå àëãåáðû ìíîæåñòâ

Îïðåäåëåíèå 1.12. Àëãåáðà  ýòî ìíîæåñòâî îáúåêòîâ ñ

îïðåäåëåííûìè íà íåì îïåðàöèÿìè, îòâå÷àþùèìè íåêîòîðûì

ñâîéñòâàì. Îáû÷íî àáñòðàêòíàÿ àëãåáðà çàäàåòñÿ êàê äâîéêà

A=<Ì, Σ>, ãäå Ì  ìíîæåñòâî îáúåêòîâ àëãåáðû (íîñèòåëü

àëãåáðû), Σ  ìíîæåñòâî îïåðàöèé (ñèãíàòóðà àëãåáðû).

Ìíîæåñòâî îïåðàöèé îïèñûâàåòñÿ ñâîèìè ñâîéñòâàìè, êîòîðûå

çàäàþòñÿ ñèñòåìîé àêñèîì äàííîé àëãåáðû.

Ìû áóäåì ðàññìàòðèâàòü àëãåáðó ïîäìíîæåñòâ íåêîòîðîãî

óíèâåðñàëüíîãî ìíîæåñòâà U. Äëÿ êðàòêîñòè â äàëüíåéøåì áóäåì

íàçûâàòü åå ïðîñòî àëãåáðîé ìíîæåñòâ.

Îïðåäåëåíèå 1.13. Îïðåäåëèì àëãåáðó ìíîæåñòâ êàê ÷åòâåðêó:

<M, ∪, ∩, ′>, ãäå M  ìíîæåñòâî-ñòåïåíü óíèâåðñàëüíîãî

ìíîæåñòâà U, à ìíîæåñòâî îïåðàöèé ñîñòîèò èç îïåðàöèé

îáúåäèíåíèÿ (∪), ïåðåñå÷åíèÿ (∩) è äîïîëíåíèÿ (′) ìíîæåñòâà

äî ìíîæåñòâà U.

Â ñîäåðæàòåëüíîé òåîðèè ìíîæåñòâ ñ ïîìîùüþ îòíîøåíèÿ

ïðèíàäëåæíîñòè ýëåìåíòîâ ìíîæåñòâó ìîæíî äîêàçàòü ñëåäóþùóþ

òåîðåìó.

Òåîðåìà 1.1. Äëÿ ëþáûõ ïîäìíîæåñòâ A, B è C íåêîòîðîãî

óíèâåðñóìà U ñëåäóþùèå ðàâåíñòâà ÿâëÿþòñÿ òîæäåñòâàìè:

1) A ∪ (B ∪ C)=(A ∪ B) ∪ C,

A ∩ (B ∩ C)=(A ∩ B) ∩ C (àññîöèàòèâíîñòü);

2) A ∪ B=B ∪ A, A ∩ B=B ∩ A (êîììóòàòèâíîñòü);

3)A∩(B∪C)=(A∩B)∪(A∩C),

A∪(B∩C)=(A∪B)∩(A∪C)(äèñòðèáóòèâíîñòü);

4) A ∪ ∅=A, A ∩ U=A;

5) A ∪ A′=U, A ∩ A′=∅.

Èç ýòèõ òîæäåñòâ, ïðèíÿòûõ êàê àêñèîìû, ìîæåò áûòü âûâåäåíà

ëþáàÿ òåîðåìà àëãåáðû ìíîæåñòâ áåç èñïîëüçîâàíèÿ ïîíÿòèÿ

ïðèíàäëåæíîñòè. Èç ïðèâåäåííûõ âûøå äåñÿòè òîæäåñòâ âèäíî,

÷òî êàæäîå ïðàâîå òîæäåñòâî ïîëó÷åíî èç ëåâîãî çàìåíîé ñèìâîëà

∪ íà ∩ è íàîáîðîò, à òàêæå çàìåíîé ∅ íà U è íàîáîðîò.

Îïðåäåëåíèå 1.14. Ðàâåíñòâî, ïîëó÷åííîå èç èñõîäíîãî çàìåíîé

âñåõ ñèìâîëîâ U íà ∅, ∅ íà U, ∪ íà ∩, ∩ íà ∪, íàçûâàåòñÿ

äâîéñòâåííûì èñõîäíîìó.

Â ïðèâåäåííîì âûøå ñïèñêå òîæäåñòâ 15 êàæäîå òîæäåñòâî

èìååò äâîéñòâåííîå åìó òîæäåñòâî. Òàêèì îáðàçîì, ìû ïðèõîäèì

ê ïðèíöèïó äâîéñòâåííîñòè: äëÿ ëþáîé òåîðåìû àëãåáðû ìíîæåñòâ

äâîéñòâåííîå åé óòâåðæäåíèå òàêæå ÿâëÿåòñÿ òåîðåìîé.

1.3.2. Òåîðåìû àëãåáðû ìíîæåñòâ

Òåîðåìà 1.2. Äëÿ ïðîèçâîëüíûõ ïîäìíîæåñòâ A è B íåêîòîðîãî

óíèâåðñàëüíîãî ìíîæåñòâà U ñïðàâåäëèâû ñëåäóþùèå

óòâåðæäåíèÿ:

6) åñëè äëÿ âñÿêîãî A A ∪ B=A, òî B=∅,

åñëè äëÿ âñÿêîãî A A∩B=A, òî B=U;

7) åñëè A ∪ B=U è A ∩ B=∅, òî B=A′;

8) A′′=A,

9) ∅′=U, U′=∅;

10) A ∪ A=A, A ∩ A=A (çàêîíû èäåìïîòåíòíîñòè);

11)A ∪ U=U, A ∩ ∅=∅;

12)A ∪(A ∩ B)=A, A ∩ (A ∪ B)=A (çàêîíû ïîãëîùåíèÿ);

13) (A ∪ B)′=A′ ∩ B′, (A ∩ B)′=A′ ∪ B′ (çàêîíû äå Ìîðãàíà)

Äîêàæåì íåêîòîðûå óòâåðæäåíèÿ, èñïîëüçóÿ òîëüêî òîæäåñòâà

15.

Óòâåðæäåíèå 6.

Äîêàçàòåëüñòâî. Ïîñêîëüêó ïî óñëîâèþ A ∪ B=A äëÿ âñåõ A,

òî ýòî âåðíî è äëÿ A=∅, ò.å. ∅ ∪ B=∅. Òîãäà èç 2) ñëåäóåò:

∅∪B=B ∪ ∅, ò.å. B ∪ ∅=∅. Ñ äðóãîé ñòîðîíû, ñîãëàñíî 4),

B∪∅= B. Îòñþäà ñëåäóåò, ÷òî B = ∅.

Óòâåðæäåíèå 7.

Äîêàçàòåëüñòâî (â ñêîáêàõ óêàçàíû íîìåðà ïðèìåíÿåìûõ

àêñèîì è óòâåðæäåíèé).

B = (4) = B ∪ ∅ =(5)= B∪(A∩A′) =(3)= (B∪A)∩(B∪A′)=

=(2)= (A∪B)∩(B∪A′) =(ïî óñë.)= U∩(B∪A′) = (5)=

=(A∪A′)∩(B∪A′) =(2)= (A′∪A)∩ (A′∪B)=(3)=

=A′∪(A∩B)=(ïî óñë.)= A′∪∅ =(4)= A′.

Äîêàçàòåëüñòâî óòâåðæäåíèÿ 8 ñëåäóåò èç óòâåðæäåíèÿ 7: àêñè-

îìû 5 ìîæíî ïåðåïèñàòü â âèäå: A′∪A=U, A ∩ A′=∅ â ñèëó

êîììóòàòèâíîñòè îïåðàöèé ∪ è ∩ (àêñèîìû 2). Òîãäà, ïî óòâåðæäå-

íèþ 7, A=A′′.

Äîêàçàòåëüñòâî îñòàëüíûõ óòâåðæäåíèé ïðåäëàãàåòñÿ ÷èòàòåëþ

ïðîâåñòè ñàìîñòîÿòåëüíî.

ÌíîæåñòâàÃëàâà 1

Îãàñòåñ äå Ìîðãàí (De Morgan) (18061871)  øîòëàíäñêèé ìàòåìàòèê è

ëîãèê. Çàíèìàëñÿ àëãåáðîé, òåîðèåé ðÿäîâ. Íåçàâèñèìî îò Äæ. Áóëÿ ïðèøåë

ê îñíîâíûì èäåÿì ìàòåìàòè÷åñêîé ëîãèêè.

1.4. Ïàðàäîêñ Áåðòðàíà Ðàññåëà

Íåîãðàíè÷åííîå ïðèìåíåíèå ïðèíöèïà àáñòðàêöèè âûçûâàåò

âîçíèêíîâåíèå ïàðàäîêñîâ â êàíòîðîâñêîé òåîðèè ìíîæåñòâ. Â

1902ã. Áåðòðàí Ðàññåë

îòêðûë ïàðàäîêñ, îñíîâàííûé íà îäíîì

ëèøü îïðåäåëåíèè ìíîæåñòâà.

Ìíîæåñòâà ëèáî ÿâëÿþòñÿ ýëåìåíòàìè ñàìèõ ñåáÿ, ëèáî íå

ÿâëÿþòñÿ. Òàê, ìíîæåñòâî àáñòðàêòíûõ ïîíÿòèé ñàìî ÿâëÿåòñÿ

àáñòðàêòíûì ïîíÿòèåì, à ìíîæåñòâî âñåõ çâåçä íà íåáå íå ÿâëÿåòñÿ

çâåçäîé. Ìíîæåñòâî çâóêîâ òàêæå ÿâëÿåòñÿ çâóêîì. Àíàëîãè÷íî,

ìíîæåñòâî âñåõ ìíîæåñòâ ñàìî åñòü ìíîæåñòâî.

Ðàññìîòðèì M  ìíîæåñòâî âñåõ ìíîæåñòâ, ÿâëÿþùèõñÿ ýëåìåí-

òàìè ñàìèõ ñåáÿ, è N  ìíîæåñòâî âñåõ ìíîæåñòâ, íå ÿâëÿþùèõñÿ

ýëåìåíòàìè ñàìèõ ñåáÿ. Ê êàêîìó æå èç ýòèõ äâóõ ìíîæåñòâ îòíåñòè

ìíîæåñòâî N? Èíûìè ñëîâàìè, ÿâëÿåòñÿ ëè N ýëåìåíòîì ñàìîãî

ñåáÿ? Åñëè N ÿâëÿåòñÿ ýëåìåíòîì ñåáÿ, ò.å. N∈N, çíà÷èò N

ÿâëÿåòñÿ ýëåìåíòîì M, ò.å. N ∈ M, íî òîãäà, ïî îïðåäåëåíèþ

ìíîæåñòâà M, N ∉ N, ò.å. N íå ÿâëÿåòñÿ ýëåìåíòîì ñàìîãî ñåáÿ.

Ïîëó÷èëè ïðîòèâîðå÷èå. Ñ äðóãîé ñòîðîíû, åñëè N íå ÿâëÿåòñÿ

ýëåìåíòîì ñàìîãî ñåáÿ, òî N åñòü ýëåìåíò N, à íå M, è N ÿâëÿåòñÿ

ýëåìåíòîì ñàìîãî ñåáÿ, ÷òî îïÿòü ÿâëÿåòñÿ ïðîòèâîðå÷èåì.

Ïàðàäîêñ Áåðòðàíà Ðàññåëà èçâåñòåí â ïîïóëÿðíîé ôîðìå êàê

ïàðàäîêñ áðàäîáðåÿ (ïàðèêìàõåðà). Â îäíîé äåðåâíå áðàäîáðåé

îáÿçóåòñÿ áðèòü âñåõ òåõ è òîëüêî òåõ æèòåëåé, êîòîðûå íå áðåþòñÿ

ñàìè. Êàê áûòü ñàìîìó áðàäîáðåþ: äîëæåí ëè îí áðèòü ñàìîãî

ñåáÿ? Î÷åâèäíî, ÷òî ëþáîé îòâåò ïðèâîäèò ê ïðîòèâîðå÷èþ.

Ïîñêîëüêó áîëüøèíñòâî ðàçäåëîâ ìàòåìàòèêè èñïîëüçóåò òåîðåòè-

êî-ìíîæåñòâåííûå ïîíÿòèÿ è ñàìà òåîðèÿ ìíîæåñòâ ìîæåò ñ÷èòàòüñÿ

îñíîâîé ýòèõ ðàçäåëîâ, òî îáíàðóæåííûå ïàðàäîêñû â íà÷àëå 20-ãî

âåêà ïîñòàâèëè ïîä ñîìíåíèå äîñòîâåðíîñòü âñåé ìàòåìàòè÷åñêîé

íàóêè â öåëîì. Âûõîäîì èç ñîçäàâøåãîñÿ ïîëîæåíèÿ áûëà àêñèîìàòè-

çàöèÿ òåîðèè ìíîæåñòâ. Îäèí èç âàðèàíòîâ òàêîé àêñèîìàòèçàöèè,

ñèñòåìà àêñèîì ÖåðìåëîÔðåíêåëÿ, áóäåò ïðèâåäåí â ãëàâå 4.

Ãëàâà 1

Áåðòðàí Ðàññåë (Russel) (18721970)  âûäàþùèéñÿ àíãëèéñêèé ìàòåìàòèê

è ôèëîñîô, ëîãèê, îáùåñòâåííûé äåÿòåëü. Îñíîâîïîëîæíèê àíãëèéñêîãî íåîðå-

àëèçìà è íåîïîçèòèâèçìà. Îäèí èç êëàññèêîâ ìàòåìàòè÷åñêîé ëîãèêè, ëàóðåàò

Íîáåëåâñêîé ïðåìèè ïî ëèòåðàòóðå (1950). (Íà ðóññêèé ÿçûê ïåðåâåäåíà

«Èñòîðèÿ çàïàäíîé ôèëîñîôèè» Á. Ðàññåëà è íåêîòîðûå äðóãèå åãî ôèëîñîô-

ñêèå è ëèòåðàòóðíî-ôèëîñîôñêèå ïðîèçâåäåíèÿ, à òàêæå íàó÷íî-ôàíòàñòè-

÷åñêèå ðàññêàçû). Îïóáëèêîâàííûå â 19101913 ãã. äâóõòîìíûå «Îñíîâàíèÿ

ìàòåìàòèêè» Áåðòðàíà Ðàññåëà è Àëüôðåäà Íîðòà Óàéòõåäà (18611947) ñîäåð-

æàò îäíó èç íàèáîëåå èçâåñòíûõ è ïðîäóìàííûõ ñèñòåì ëîãè÷åñêîãî îáîñíîâà-

íèÿ ìàòåìàòèêè, îêàçàâøóþ áîëüøîå âëèÿíèå íà Ä.Ãèëüáåðòà (18621947).

Ãëàâà 2. ÒÅÎÐÈß ÎÒÍÎØÅÍÈÉ

2.1. Îñíîâíûå ïîíÿòèÿ

Äëÿ îáîçíà÷åíèÿ êàêîé-ëèáî ñâÿçè ìåæäó îáúåêòàìè èëè

ïîíÿòèÿìè â ìàòåìàòèêå ÷àñòî ïîëüçóþòñÿ ïîíÿòèåì «îòíîøåíèå».

Íàïðèìåð, ñâîéñòâî ýëåìåíòà ïðèíàäëåæàòü èëè íå ïðèíàäëåæàòü

ìíîæåñòâó ÿâëÿåòñÿ îòíîøåíèåì «x∈X», ïðè÷åì, åñëè ýëåìåíò

ïðèíàäëåæèò ìíîæåñòâó, òî îòíîøåíèå âûïîëíåíî, à åñëè íå

ïðèíàäëåæèò, òî íå âûïîëíåíî. Âêëþ÷åíèå ìíîæåñòâà â äðóãîå

ìíîæåñòâî «X ⊆ Y» òàêæå ÿâëÿåòñÿ îòíîøåíèåì. Íà ìíîæåñòâå

ëþäåé çàäàíî îòíîøåíèå ðîäñòâà, íàïðèìåð, «x  îòåö y». Åñëè

âçÿòü êîíêðåòíûõ ëþäåé è ïîäñòàâèòü èõ èìåíà âìåñòî x è y, òî ìû

ïîëó÷èì èñòèííîå èëè ëîæíîå âûñêàçûâàíèå, íàïðèìåð: «Ëàèé

îòåö Ýäèïà» èñòèííîå âûñêàçûâàíèå, «Ïîëèá  îòåö Ýäèïà»



ëîæíîå. Â ýòîì ñìûñëå îòíîøåíèå òàêæå ÿâëÿåòñÿ ïðåäèêàòîì,

êîòîðûé îáðàùàåòñÿ â èñòèííîå èëè ëîæíîå âûñêàçûâàíèå ïðè

ïîäñòàíîâêå â íåãî êîíêðåòíûõ ýëåìåíòîâ èç îáëàñòè îïðåäåëåíèÿ.

Ðàññìîòðèì åùå îäíó îïåðàöèþ íàä ìíîæåñòâàìè.

Îïðåäåëåíèå 2.1. Äåêàðòîâûì ïðîèçâåäåíèåì ìíîæåñòâ X è Y

íàçûâàåòñÿ ìíîæåñòâî âñåõ óïîðÿäî÷åííûõ ïàð <x, y>, òàêèõ,

÷òî x∈X è y∈Y.

Ýòî îáîçíà÷àåòñÿ êàê X×Y ={<x, y> | x ∈ X, y ∈ Y}.

Óïîðÿäî÷åííàÿ ïàðà ýëåìåíòîâ <x,ó> îäíîçíà÷íî îïðåäåëÿåòñÿ

÷åðåç x è y. Êðîìå òîãî, åñëè <x,ó>=<u,v>, òî x=u è ó=v.

Ïðèíÿòî íàçûâàòü x ïåðâîé, à y  âòîðîé êîîðäèíàòîé óïîðÿäî-

÷åííîé ïàðû <x, ó>.

Ïðèìåð. Ïóñòü äàíû ìíîæåñòâà X={1, 2} è Y={2, 3, 4}.

Äåêàðòîâî ïðîèçâåäåíèå ýòèõ äâóõ ìíîæåñòâ: X×Y={<1,2>,

<1,3>, <1,4>, <2,2>, <2,3>, <2,4>}. Ðàññìîòðèì ïîäìíîæåñòâî

ýòîãî äåêàðòîâîãî ïðîèçâåäåíèÿ A={<1,2>, <1,3>, <1,4>, <2,3>,

<2,4>}. Ýòî íå ÷òî èíîå, êàê îòíîøåíèå

: x < y  «x ìåíüøå y».

Íà òîì æå ìíîæåñòâå óïîðÿäî÷åííûõ ïàð ìîæíî âûäåëèòü åùå

îäíî îòíîøåíèå ρ

: y=x+1  ýòî ïîäìíîæåñòâî {<1,2>, <2,3>}.

Äðóãîå îòíîøåíèå ρ

: x=y  ýòî ïîäìíîæåñòâî {<2,2>}.

Ìíîæåñòâî óïîðÿäî÷åííûõ ïàð îáðàçóåò áèíàðíîå îòíîøåíèå.

Îïðåäåëåíèå 2.2. Áèíàðíîå îòíîøåíèå åñòü ïîäìíîæåñòâî äåêàð-

òîâîãî ïðîèçâåäåíèÿ äâóõ ìíîæåñòâ.

Ýäèï, Ïîëèá è Ëàèé  ãåðîè òðàãåäèè Ñîôîêëà «Öàðü Ýäèï». Ýäèï áûë íå

ðîäíûì ñûíîì Ïîëèáà è ïîòîìó âòîðîå âûñêàçûâàíèå ëîæíî. Ðîäíûì æå

îòöîì Ýäèïà áûë Ëàèé, è ïîòîìó ïåðâîå âûñêàçûâàíèå èñòèííî.

16 17

Áèíàðíîå îòíîøåíèå îáîçíà÷àåòñÿ òàê: <x,ó>∈ρ èëè xρó. Ýòè

âûðàæåíèÿ ýêâèâàëåíòíû è ÷èòàþòñÿ êàê «x íàõîäèòñÿ â îòíîøåíèè

ρ ê ó».

Åñòåñòâåííûì îáîáùåíèåì ïîíÿòèÿ áèíàðíîãî îòíîøåíèÿ ÿâëÿ-

åòñÿ ïîíÿòèå n-àðíîãî (n-ìåñòíîãî) îòíîøåíèÿ, îïðåäåëÿåìîãî êàê

ïîäìíîæåñòâî äåêàðòîâà ïðîèçâåäåíèÿ n ìíîæåñòâ:

×X

×...×X

={<x

,x

,...,x

> | x

∈ X

,x

∈X

,...,x

∈X

n-àðíîå îòíîøåíèå ïðåäñòàâëÿåò ñîáîé ìíîæåñòâî óïîðÿäî÷åí-

íûõ n-îê (÷èòàåòñÿ: «ýíêà»). Óïîðÿäî÷åííóþ n-êó íàçûâàþò èíà÷å

êîðòåæåì. Ïîäìíîæåñòâî êîðòåæåé èç n ýëåìåíòîâ îáðàçóåò n-

àðíîå îòíîøåíèå. Ïðè n=2 èìååò ìåñòî áèíàðíîå îòíîøåíèå, ïðè

n=3 èñïîëüçóåòñÿ òåðìèí òåðíàðíîå îòíîøåíèå.

Ïðèìåðû.

1. Äëÿ íåêîòîðûõ îòíîøåíèé ïðèíÿòû ñïåöèàëüíûå îáîçíà÷åíèÿ:

ðàâåíñòâî: x=y;

òîæäåñòâî: x≡y;

íåðàâåíñòâà: x ≥ y, x ≤ y, x <y, x> y;

ïðèíàäëåæíîñòü: x ∈ Y, x ∉ Y;

âêëþ÷åíèå: X ⊆ Y, X ⊂ Y;

êîíãðóýíòíîñòü: x ≅ y.

2. Ìíîæåñòâî {<2,4>,<7,3>,<3,3>,<2,1>}, áóäó÷è ìíîæåñòâîì

óïîðÿäî÷åííûõ ïàð, åñòü áèíàðíîå îòíîøåíèå. Íå èìåÿ íèêàêîãî

êîíêðåòíîãî çíà÷åíèÿ, ýòî îòíîøåíèå, åñòåñòâåííî, íå èìååò è

ñïåöèàëüíîãî íàçâàíèÿ.

3. Åñëè m îáîçíà÷àåò îòíîøåíèå ìàòåðèíñòâà, òî <Äæåéí,Äæîí>∈m

îçíà÷àåò, ÷òî Äæåéí ÿâëÿåòñÿ ìàòåðüþ Äæîíà.

4. «x è y  ðîäèòåëè z»  òåðíàðíîå îòíîøåíèå.

5. Ïðèìåðîì n-àðíîãî îòíîøåíèÿ, ãäå n=4, ìîæåò ñëóæèòü òàáëèöà:

Îïðåäåëåíèå 2.3. Îáëàñòüþ îïðåäåëåíèÿ áèíàðíîãî îòíîøåíèÿ

ρ (îáîçíà÷åíèå: D

) íàçûâàþò ìíîæåñòâî ïåðâûõ êîîðäèíàò

ýëåìåíòîâ èç ρ, îáëàñòüþ çíà÷åíèé îòíîøåíèÿ ρ (îáîçíà÷åíèå:

)  ìíîæåñòâî âòîðûõ êîîðäèíàò ýëåìåíòîâ èç ρ.

Íàïðèìåð, êàê îáëàñòüþ îïðåäåëåíèÿ, òàê è îáëàñòüþ çíà÷åíèé

îòíîøåíèÿ âêëþ÷åíèÿ äëÿ ïîäìíîæåñòâ ìíîæåñòâà U ÿâëÿåòñÿ

ìíîæåñòâî ℘(U); îáëàñòüþ îïðåäåëåíèÿ äëÿ îòíîøåíèÿ ìàòå-

ðèíñòâà ñëóæèò ìíîæåñòâî âñåõ ìàòåðåé, â òî âðåìÿ, êàê îáëàñòü

çíà÷åíèé ýòîãî îòíîøåíèÿ  ìíîæåñòâî âñåõ ëþäåé.

2.2. Ñïîñîáû çàäàíèÿ îòíîøåíèé

2.2.1. Ãðàôèê îòíîøåíèÿ

Àíàëèòè÷åñêàÿ ãåîìåòðèÿ ïëîñêîñòè îñíîâûâàåòñÿ íà äîïóùå-

íèè î òîì, ÷òî ìåæäó òî÷êàìè åâêëèäîâîé ïëîñêîñòè è äåêàðòîâûì

ïðîèçâåäåíèåì R×R ñóùåñòâóåò âçàèìíî îäíîçíà÷íîå ñîîòâåòñòâèå.

Êàæäîé òî÷êå íà ïëîñêîñòè ñîîòâåòñòâóþò åå êîîðäèíàòû 

óïîðÿäî÷åííàÿ ïàðà <x, y>. Ïîýòîìó îòíîøåíèå íà ìíîæåñòâå R

ìîæíî èçîáðàæàòü íà ïëîñêîñòè íåêîòîðîé êîíôèãóðàöèåé èëè

ìíîæåñòâîì òî÷åê. Íàïðèìåð, îòíîøåíèå ðàâåíñòâà ìîæíî èçîáðà-

çèòü â âèäå ïðÿìîé y = x â äåêàðòîâîé ñèñòåìå êîîðäèíàò.

Îïðåäåëåíèå 2.4. Åñëè îñíîâíûì ïðåäìåòîì èçó÷åíèÿ ñëóæàò

îòíîøåíèÿ íà ìíîæåñòâå äåéñòâèòåëüíûõ ÷èñåë R, òî ìíîæåñòâî

òî÷åê, ñîîòâåòñòâóþùèõ ýëåìåíòàì îòíîøåíèÿ, íàçûâàþò

ãðàôèêîì ýòîãî îòíîøåíèÿ.

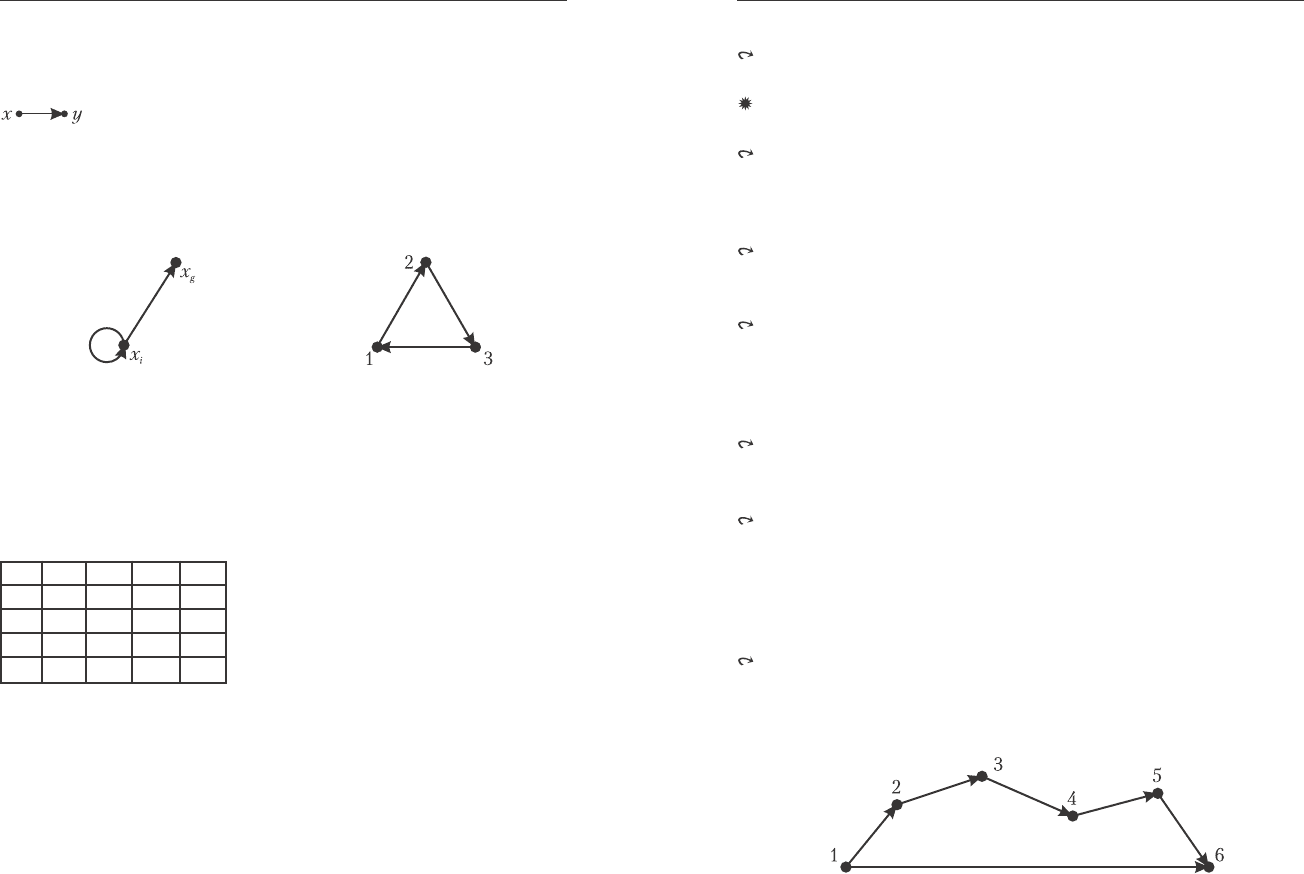
Íèæå íà ðèñ. 2.12.4 ïðèâîäÿòñÿ ÷åòûðå ïðèìåðà îòíîøåíèé,

äëÿ êàæäîãî èç êîòîðûõ ñõåìàòè÷åñêè ïðåäñòàâëåí åãî ãðàôèê. Â

òåõ ñëó÷àÿõ, êîãäà ãðàôèê ÿâëÿåòñÿ ÷àñòüþ ïëîñêîñòè, ýòà ÷àñòü

ïëîñêîñòè íà ÷åðòåæå çàøòðèõîâûâàåòñÿ.

Òåîðèÿ îòíîøåíèéÃëàâà 2

Ôàìèëèÿ Ãîä ðîæä. Ìåñòî æèòåëüñòâà Îáðàçîâàíèå

1 Èâàíîâ 1958 Êèåâ âûñøåå

2 ... ... ... ...

{<x, y>∈R×R|y=x}

Ðèñ. 2.1. Ðèñ. 2.2.

{<x, y>∈R×R|y≥x}

{<x, y>∈R×R|0≤x≤2 èëè

0≤y≤1}

Ðèñ. 2.3. Ðèñ. 2.4.

{<x, y>∈R×R|0≤x≤2 è

0≤y≤1}

18 19

2.2.2. Ãðàôè÷åñêèé ñïîñîá çàäàíèÿ ìíîæåñòâà

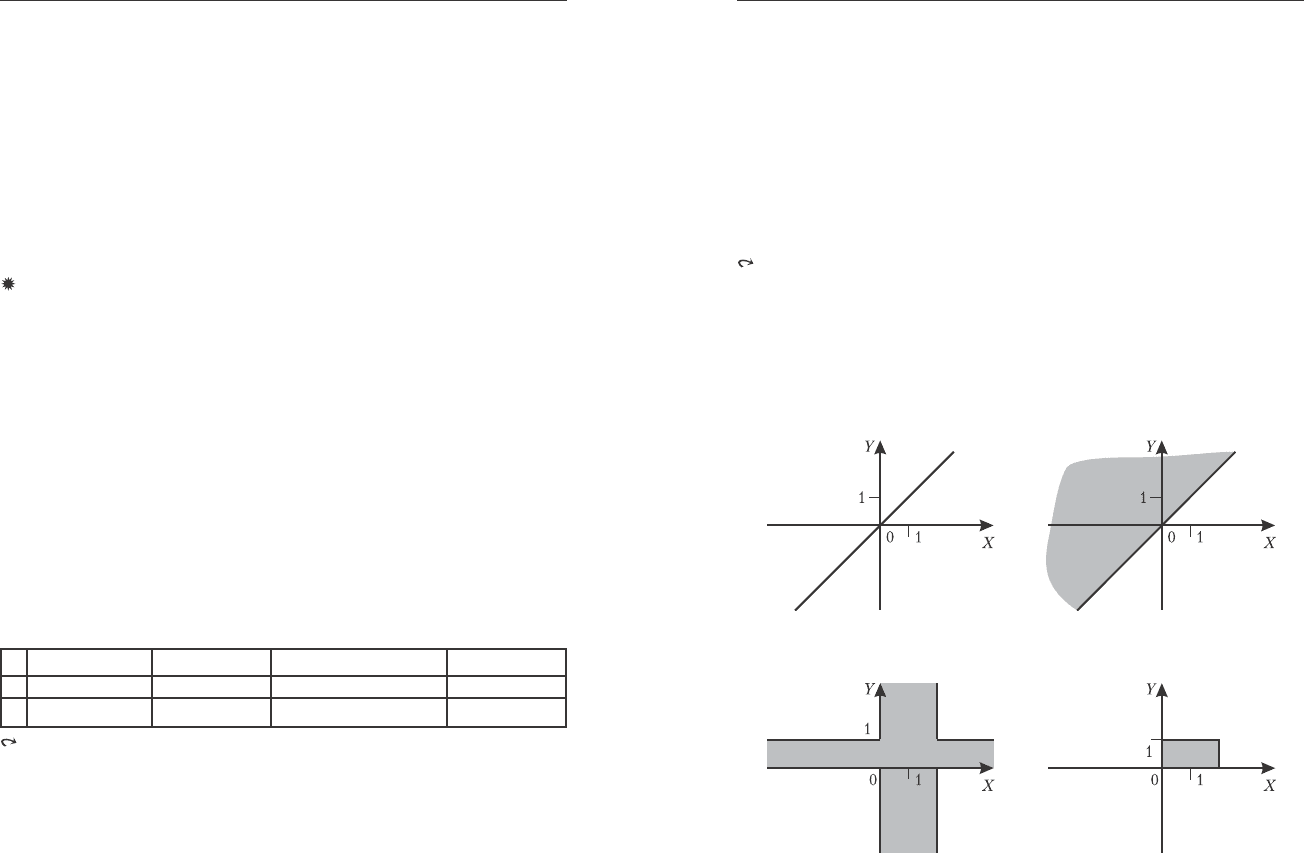
Åñëè çàäàíî îòíîøåíèå xρy, x∈X, y∈Y, òî ýëåìåíòû ìíîæåñòâ

X è Y ìîæíî èçîáðàæàòü òî÷êàìè íà ïëîñêîñòè, à óïîðÿäî÷åííóþ

ïàðó  ëèíèåé ñî ñòðåëêîé (äóãîé), íàïðàâëåííîé îò x ê y:

. Òîãäà îòíîøåíèå íà êîíå÷íîì ìíîæåñòâå ýëåìåíòîâ

ìîæåò áûòü ïðåäñòàâëåíî â âèäå ãðàôà.

Íàïðèìåð, îòíîøåíèå ρ

= {<x

, x

>, <x

, x

>} ìîæåò áûòü

ïðåäñòàâëåíî â âèäå ãðàôà, èçîáðàæåííîãî íà ðèñ. 2.5. Îòíîøåíèå

={<1, 2>, <2, 3>, <3, 1>} ìîæåò áûòü ïðåäñòàâëåíî â âèäå îðèåí-

òèðîâàííîãî ãðàôà (ñì. ðèñ.2.6).

2.2.3. Ìàòðè÷íûé ñïîñîá çàäàíèÿ îòíîøåíèé

Çàäàäèì îòíîøåíèå ρ: «x äðóæèò ñ ó» íà ìíîæåñòâå M, ãäå

Ì={a

, a

} ìíîæåñòâî ïåðñîíàæåé. Ýòî îòíîøåíèå ìîæíî

ïðåäñòàâèòü â âèäå òàáëèöû (ìàòðèöû), ýëåìåíòû êîòîðîé ðàâíû

åäèíèöå, åñëè ìåæäó ñîîòâåòñòâóþùèìè ýëåìåíòàìè åñòü îòíîøåíèå

äðóæáû, è íóëþ â ïðîòèâíîì ñëó÷àå.

Èç ýòîé òàáëèöû âèäíî, ÷òî a

äðóæèò ñ a

, a

íå äðóæèò íè ñ êåì,

êðîìå êàê ñ ñàìèì ñîáîé, à a

äðóæèò

ñî âñåìè, êðîìå a

. Òàêîé ñïîñîá

çàäàíèÿ îòíîøåíèé íàçûâàåòñÿ

ìàòðè÷íûì ñïîñîáîì. Â ýòîì ñëó÷àå

îòíîøåíèå ρ∈X×Y ïðåäñòàâëÿåòñÿ â

âèäå ìàòðèöû A=||a

|| ñ ýëåìåíòàìè a

, ãäå i  íîìåð ñòðîêè, g 

íîìåð ñòîëáöà; a

=1, åñëè ýëåìåíòû x

è y

íàõîäÿòñÿ â îòíîøåíèè

, è a

=0 â ïðîòèâíîì ñëó÷àå.

Åñëè ||a

||= 0, ò.å. äëÿ âñåõ i è g a

= 0, òî ρ≡0  ïóñòîå îòíîøåíèå;

åñëè ||a

||= 1, ò.å. äëÿ âñåõ i è g a

= 1, òî ρ≡1  ïîëíîå îòíîøåíèå.

2.3. Îïåðàöèè íàä îòíîøåíèÿìè

Òàê êàê êàæäîå îòíîøåíèå åñòü ìíîæåñòâî, òî íàä îòíîøåíèÿìè

ìîæíî âûïîëíÿòü âñå îïåðàöèè, îïðåäåëåííûå äëÿ ìíîæåñòâ. Â

ðåçóëüòàòå ôîðìèðóþòñÿ íîâûå, áîëåå ñëîæíûå îòíîøåíèÿ.

2.3.1. Òåîðåòèêîìíîæåñòâåííûå îïåðàöèè

Îïðåäåëåíèå 2.5. Ïåðåñå÷åíèåì îòíîøåíèé α è β íàçûâàåòñÿ îòíî-

øåíèå, îïðåäåëÿåìîå ïåðåñå÷åíèåì ñîîòâåòñòâóþùèõ ìíîæåñòâ.

Ïðèìåð. Ïóñòü α: «x ≥ y», β: «x > y». Òîãäà ïåðåñå÷åíèå ∫∑

α∩β åñòüîòíîøåíèå «x > y».

Îïðåäåëåíèå 2.6. Îáúåäèíåíèå îòíîøåíèé α è β îáðàçóåòñÿ îáúå-

äèíåíèåì ñîîòâåòñòâóþùèõ ìíîæåñòâ.

Ïðèìåð. Ïóñòü α: x > y, β: «x=y», òîãäà èõ îáúåäèíåíèå åñòü

îòíîøåíèå α∪β: x ≥ y.

Îïðåäåëåíèå 2.7. Âêëþ÷åíèå îòíîøåíèé: α âêëþ÷åíî â β, åñëè

ìíîæåñòâî âñåõ ïàð <x,y>∈α ñîäåðæèòñÿ è â îòíîøåíèè β,

ò.å. α⊆β, åñëè äëÿ êàæäîãî <x,y>∈α, <x,y>∈β.

Îïðåäåëåíèå 2.8. Åñëè α  îòíîøåíèå, çàäàííîå íà Ì, òî

îáðàòíîå îòíîøåíèå α

1

îïðåäåëÿåòñÿ êàê xα

1

y=yαx.

Íàïðèìåð, åñëè α: «x > y», ãäå x, y∈R, òî îáðàòíîå åìó îòíîøå-

íèå α

1

: «y > x», èëè «x<y». Åñëè α: «x ñåñòðà ó», ãäå x∈{æåí-

ùèíû}, y∈{ìóæ÷èíû}, òî îáðàòíîå îòíîøåíèå α

1

 «y ñåñòðà x».

Îïðåäåëåíèå 2.9. Äîïîëíåíèåì áèíàðíîãî îòíîøåíèÿ

ìåæäó

ýëåìåíòàìè x∈A è y∈B, ñ÷èòàåòñÿ ìíîæåñòâî ρ

′= (A×B)\

êîòîðîå òîæå ÿâëÿåòñÿ îòíîøåíèåì.

Îïðåäåëåíèå 2.10. Îòíîøåíèÿ α è β ìîãóò îáðàçîâûâàòü ïðîèçâå-

äåíèå îòíîøåíèé αβ, êîòîðîå ñàìî ÿâëÿåòñÿ îòíîøåíèåì, ò.å. xαβy,

x, y∈M, åñëè ñóùåñòâóåò òàêîé ýëåìåíò z∈M, ÷òî xαz è zβy.

Íàïðèìåð, ïóñòü α: «x  ìàòü ó», β: «x îòåö ó». Òîãäà ñóùåñòâóåò

òàêîå b, ÷òî aαb è bβc, ò.å. «a  ìàòü b» è «b  îòåö c». Òîãäà

ïðîèçâåäåíèå ýòèõ îòíîøåíèé: «a  áàáóøêà c».

Îïðåäåëåíèå 2.11. Îòíîøåíèå α

íàçûâàåòñÿ òðàíçèòèâíûì

çàìûêàíèåì îòíîøåíèÿ α, îïðåäåëåííîãî íà ìíîæåñòâå M, òîãäà

è òîëüêî òîãäà, êîãäà ñóùåñòâóþò òàêèå aα

b, ÷òî aαz

αz

,z

αz

,...,z

n1

αb.

Ðèñ. 2.7. Òðàíçèòèâíîå çàìûêàíèå îòíîøåíèÿ x < y.

Òåîðèÿ îòíîøåíèéÃëàâà 2

Ðèñ. 2.5. Ãðàô îòíîøåíèÿ ρ

. Ðèñ. 2.6. Ãðàô îòíîøåíèÿ ρ

1010

0100

1011

0011