Таран Т.А. Основы дискретной математики
Подождите немного. Документ загружается.


100 101
ïîäìíîæåñòâîì. Åñëè L
1
=L
2
=...=L
n
, òî
12
{} {}
{}
12
...
n
xx
x
n
LL L
×××
=L
E
,
è ìû ñíîâà ïðèõîäèì ê ïîíÿòèþ íå÷åòêîãî ïîäìíîæåñòâà â òîì æå
ñìûñëå, êàê è ðàíüøå.
Åñëè L
1,
L
2
, L
3
ðåøåòêè, òî
()
1
2
3
L
L
L
òîæå ðåøåòêà, è îäèí
ýëåìåíò åå ýòî íå÷åòêîå ìíîæåñòâî 2-ãî ïîðÿäêà.
Ìîæíî ïîéòè äàëüøå è îïðåäåëèòü íå÷åòêèå ïîäìíîæåñòâà
áîëåå âûñîêèõ ïîðÿäêîâ (n > 2).
Ïðèìåð. Ïóñòü L
1
={A, B, C}, L
2
={a, b}, L
3
={a, b}. Èññëåäóåì
ïðåäñòàâëåíèå:
()
1
2
3
L
L
L
. Ïîñòðîèì ñíà÷àëà
1
2
L
L
. Ýòî áóäóò íå÷åòêèå
ìíîæåñòâà:
F
1
={A/a, B/a, C/a}, F
2
={A/a, B/a, C/b},
F
3
={A/a, B/b, C/a}, F
4
={A/a, B/b, C/b},
F
5
={A/b, B/a, C/a}, F
6
={A/b, B/a, C/b},
F
7
={A/b, B/b, C/a}, F
8
={A/b, B/b, C/b}.
Çàïèøåì F
1
F
8
ñëåäóþùèì îáðàçîì:
1
2
L
L
={~Faaa, ~Faab, ~Faba,
~Fabb, ~Fbaa, ~Fbab, ~Fbba, ~Fbbb}. Êàæäûé èç ýòèõ ýëåìåíòîâ
íå÷åòêîå ìíîæåñòâî 1-ãî ïîðÿäêà. Âîçâåäåì òåïåðü L
3
â ñòåïåíü
1
2
L
L
. Ýòà ñòåïåíü ñîäåðæèò 2
8
=256 ýëåìåíòîâ, íàïðèìåð:
~~F
1
={~Faaa/a, ~Faab/a, ~Faba/a, ~Fabb/a, ~Fbaa/a, ~Fbab/a,
~Fbba/a, ~Fbbb/a},
~~F
2
={~Faaa/a, ~Faab/a, ~Faba/a, ~Fabb/a, ~Fbaa/a, ~Fbab/a,
~Fbba/a, ~Fbbb/b},
~~F
3
={~Faaa/a, ~Faab/a, ~Faba/a, ~Fabb/a, ~Fbaa/a, ~Fbab/a,
~Fbba/b, ~Fbbb/a}, è ò.ä.
Ñëåäóåò îáðàòèòü âíèìàíèå, ÷òî
()
1
2
3
L
L
L
≠
()
1
2
3
L
L
L
. Âòîðàÿ ñòåïåíü
äàåò íàì íå÷åòêîñòü äðóãîãî òèïà.
7.4. Ðåøåòî÷íûå ìíîãî÷ëåíû
Îïðåäåëåíèå 7.12. Èíäèâèäóàëüíûå ïåðåìåííûå x, y, z, ÿâ-
ëÿþòñÿ ìíîãî÷ëåíàìè âåñà 1. Åñëè p, q ðåøåòî÷íûå ìíîãî-
÷ëåíû âåñîâ n, m ñîîòâåòñòâåííî, òî p∨q, p∧q íàçûâàþòñÿ
ðåøåòî÷íûìè ìíîãî÷ëåíàìè âåñà n + m.
Òåîðåìà 7.4. Â ëþáîé ðåøåòêå L ïîäðåøåòêà F
2
, ïîðîæäåííàÿ
äâóìÿ ýëåìåíòàìè x è y, ñîñòîèò èç ýëåìåíòîâ x, y, x∧y=v,
x∨y=u, äëÿ êîòîðûõ îïåðàöèè ∨ è ∧ çàäàþòñÿ, êàê ïîêàçàíî
íà ðèñ.7.8.
Äîêàçàòåëüñòâî. Ñîãëàñíî L4, x ∧ u = x, à èç
L3, L1 ñëåäóåò, ÷òî x ∨ u = x ∨ (x ∨ y) =
=(x∨x)∨ y = x ∨ y = u. Â ñèëó L4, u ∨ v =
=x∨y ∨ (x ∧ y) = x ∨ y = u. Îñòàëüíûå ñëó÷àè
äîêàçûâàþòñÿ àíàëîãè÷íî, íà îñíîâàíèè ñèì-
ìåòðè÷íîñòè ìåæäó x è y è äâîéñòâåííîñòè.
Ðåøåòêó F
2
íàçûâàþò ñâîáîäíîé ðåøåòêîé ñ
äâóìÿ ïîðîæäàþùèìè x è y. Îíà ñîäåðæèò
÷åòûðå ýëåìåíòà è ÿâëÿåòñÿ áóëåâîé ðåøåòêîé.
Ðåøåòî÷íûå ìíîãî÷ëåíû îò òðåõ è áîëåå
ïåðåìåííûõ ìîãóò áûòü óñòðîåíû î÷åíü ñëîæíî,
îäíàêî ó íèõ åñòü íåñêîëüêî ïðîñòûõ ñâîéñòâ.
Òåîðåìà 7.5.  ëþáîé ∨-ïîëóðåøåòêå êàæäûé ìíîãî÷ëåí îò x
1
,
x
2
, , x
r
ýêâèâàëåíòåí îáúåäèíåíèþ ∨
S
x
i
íåêîòîðîãî íåïóñòîãî
ìíîæåñòâà ýòèõ ïåðåìåííûõ.
Äîêàçàòåëüñòâî. Ñîãëàñíî L2, L3 êàæäûé òàêîé ìíîãî÷ëåí
ýêâèâàëåíòåí îáúåäèíåíèþ íåêîòîðûõ ïåðåìåííûõ x
2
, , x
r
â
óêàçàííîì ïîðÿäêå, âîçìîæíî, ñ ïîâòîðåíèÿìè. Òîãäà, íà îñíîâàíèè
L1 ìîæíî çàìåíèòü ïîâòîðÿþùèåñÿ âõîæäåíèÿ îäíîãî è òîãî æå
ñèìâîëà îäíèì âõîæäåíèåì ýòîãî ñèìâîëà.
Òåîðåìà 7.6. Â ëþáîé äèñòðèáóòèâíîé ðåøåòêå êàæäûé
ìíîãî÷ëåí ýêâèâàëåíòåí íåêîòîðîìó îáúåäèíåíèþ ïåðåñå÷åíèé
è, äâîéñòâåííî, ïåðåñå÷åíèþ îáúåäèíåíèé:
p(x
1
, x
2
, , x
r
)= ∨
a ∈ A
{∧
Sa
x
i
}=∧
δ ∈ D
{∨
Tδ
x
i
},
ãäå S
a
, T
δ
íåïóñòûå ìíîæåñòâà èíäåêñîâ, ∨, ∧ îáúåäèíåíèå è
ïåðåñå÷åíèå êîíå÷íîãî ÷èñëà ÷ëåíîâ.
Äîêàçàòåëüñòâî. Êàæäûé ýëåìåíò x
i
ìîæíî çàïèñàòü òàêèì îáðà-
çîì, ñ÷èòàÿ A (èëè D) ñåìåéñòâîì ìíîæåñòâ, ñîñòîÿùèì èç åäèí-
ñòâåííîãî îäíîýëåìåíòíîãî ìíîæåñòâà {x
i
}. Ñ äðóãîé ñòîðîíû,
èñïîëüçóÿ L1 L3, ïîëó÷àåì: ∨
a∈A
{∧
Sa
x
i
}∨ ∨
b∈B
{∧
Sb
x
i
}=
=∨
A∪B
{∧
Sc
x
i
}.
Âñëåäñòâèå äèñòðèáóòèâíîñòè ðåøåòêè èìååì: ∨
a∈A
{∧
Sa
x
i
}∧
∧∨
b∈B
{∧
Sb
x
i
}= ∨
A×B
{∧
Sab
x
i
}.
7.5. Ãîìîìîðôèçìû è èäåàëû
7.5.1. Ãîìîìîðôèçì ðåøåòîê
Îïðåäåëåíèå 7.13. Èçîòîííîå îòîáðàæåíèå ϕ: L→M ðåøåòêè
L â ðåøåòêó M íàçûâàåòñÿ ∨-ãîìîìîðôèçìîì, åñëè
ϕ(x ∨ y)= ϕ(x)∨ ϕ(y) ∀x,y ∈ L, (1)
∧-ãîìîìîðôèçìîì, åñëè
Ãëàâà 7 Ñòðîåíèå è ïðåäñòàâëåíèå ðåøåòîê
Ðèñ. 7.8.
Ðåøåòêà
ñäâóìÿ
ïîðîæäàþùèìè
102 103
ϕ(x ∧ y)= ϕ(x)∧ ϕ(y) ∀x,y ∈ L,(1')
è ïðîñòî ãîìîìîðôèçìîì (ìîðôèçìîì), åñëè âûïîëíÿåòñÿ (1) è (1').
Òàêèì îáðàçîì, ãîìîìîðôèçì ðåøåòîê ýòî ôóíêöèîíàëüíîå
îòîáðàæåíèå, ñîõðàíÿþùåå ðåøåòî÷íûå îïåðàöèè, ò.å. ïåðåâîäÿùåå
îáúåäèíåíèå â îáúåäèíåíèå, ïåðåñå÷åíèå â ïåðåñå÷åíèå.
Îïðåäåëåíèå 7.14. Ãîìîìîðôèçì íàçûâàþò:
1)èçîìîðôèçìoì, åñëè îí ÿâëÿåòñÿ âçàèìíî îäíîçíà÷íûì
ñîîòâåòñòâèåì (áèåêöèåé);
2)íàëîæåíèåì, èëè ýïèìîðôèçìîì, åñëè îí îòîáðàæàåò L íà M,
ò.å. åñëè îòîáðàæåíèå ϕ: L→M ÿâëÿåòñÿ ñþðúåêöèåé;
3)âëîæåíèåì, èëè ìîíîìîðôèçìîì, åñëè ðàçëè÷íûå ýëåìåíòû L
îòîáðàæàþòñÿ â ðàçëè÷íûå ýëåìåíòû M (îäíîçíà÷íîå ñîîò-
âåòñòâèå), ò.å. îòîáðàæåíèå ϕ: L→M ÿâëÿåòñÿ èíúåêöèåé;
4)ýíäîìîðôèçìîì, åñëè L=M;
5)àâòîìîðôèçìîì, åñëè L=M è îòîáðàæåíèå èçîìîðôèçì.
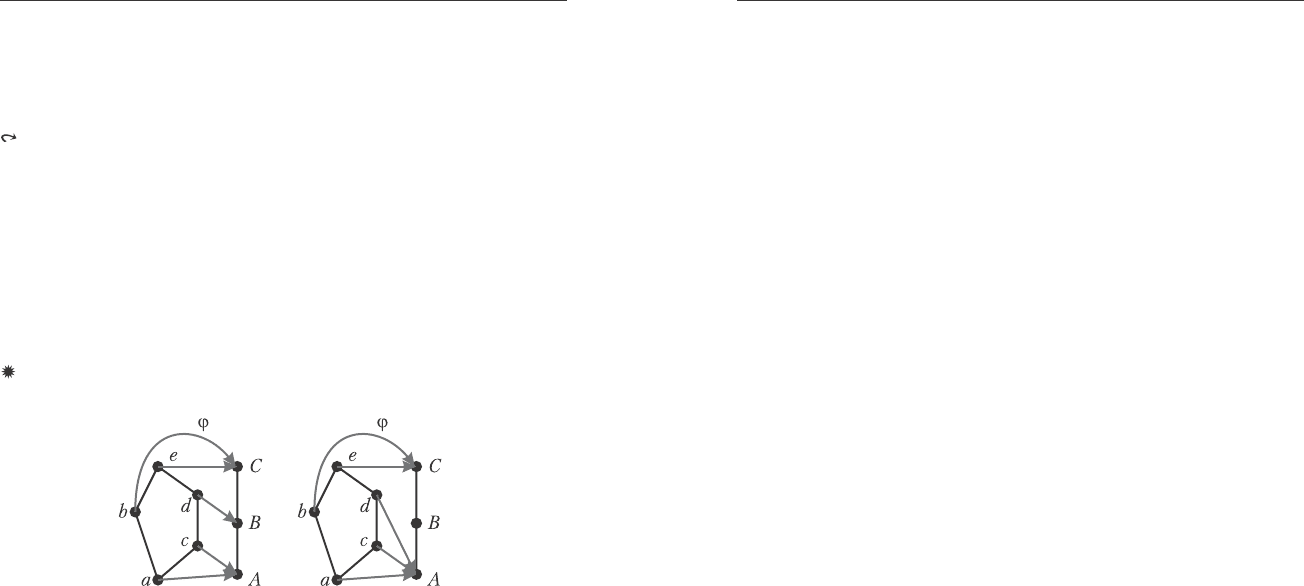
Ïðèìåð. Ðàññìîòðèì îòîáðàæåíèå ϕ ìíîæåñòâà L= {a, b, c, d,e}
íà ìíîæåñòâî M={A, B,C} (ðèñ. 7.9, a).
Ðèñ. 7.9. à) ∨-ãîìîìîðôèçì, á) ãîìîìîðìîðôèçì.
Ïðîâåðèì, ÿâëÿåòñÿ ëè îíî èçîòîííûì. Ðàññìîòðèì âñå öåïè
ìàêñèìàëüíîé äëèíû è èõ îáðàçû.
Äëÿ öåïè a ≤b ≤e âûïîëíåíî ϕ(a)≤ ϕ(b)≤ ϕ(e), òàê êàê
A≤C≤C. Äëÿ öåïè a ≤c≤d≤e ñâîéñòâî èçîòîííîñòè òàêæå
âûïîëíåíî, òàê êàê
a ≤c, ϕ(a)=A, ϕ(c)=A, A≤A, c ≤d, ϕ(c) =A, ϕ(d) = B, A≤B,
d ≤e, ϕ(d)=B, ϕ(e) = C, B≤C, b ≤e, ϕ(b)=C, ϕ(b) = C, C≤C.
Îòîáðàæåíèå ϕ èçîòîííî. Ïðîâåðèì, ÿâëÿåòñÿ ëè îíî
∨-ãîìîìîðôèçìîì. Â ñèëó èçîòîííîñòè îòîáðàæåíèÿ, îíî ñîõðàíÿåò
îïåðàöèè ∨ è ∧, ïîýòîìó äîñòàòî÷íî ïðîâåðèòü ñîõðàíåíèå ýòèõ
îïåðàöèé äëÿ íåñðàâíèìûõ ýëåìåíòîâ:
ϕ(b∨c)=ϕ(e) = C; ϕ(b)∨ϕ(c) = C∨A=C,
ϕ(b∨d)=ϕ(e) = C; ϕ(b)∨ϕ(d) = C∨B=C.
Îòîáðàæåíèå ϕ ñîõðàíÿåò ∨, ñëåäîâàòåëüíî, ÿâëÿåòñÿ
∨-ãîìîìîðôèçìîì. Îäíàêî îíî íå ÿâëÿåòñÿ ∧-ãîìîìîðôèçìîì, òàê
êàê ϕ(b∧d)=ϕ(a) = A, íî ϕ(b)∧ϕ(d) = C∧B=B, ò.å. ñâîéñòâî
ñîõðàíåíèÿ ∧ íå âûïîëíåíî. Ïîýòîìó îòîáðàæåíèå ϕ íå ÿâëÿåòñÿ
ãîìîìîðôèçì. Íà ðèñ. 7.9, á ïîêàçàíî îòîáðàæåíèå, êîòîðîå ÿâëÿ-
åòñÿ ãîìîìîðôèçìîì.
7.5.2. Ïîíÿòèå èäåàëà
Ïðè ãîìîìîðôèçìå ðåøåòêè L â ðåøåòêó M ìíîæåñòâî
ýëåìåíòîâ èç L, ïåðåõîäÿùèõ â îäèí è òîò æå ýëåìåíò M, íå ìîæåò
áûòü ïðîèçâîëüíûì. Åñëè ϕ ãîìîìîðôèçì ðåøåòîê è ϕ(a)=ϕ(b),
òî, ïîñêîëüêó ϕ ñîõðàíÿåò îïåðàöèè, â ñèëó èäåìïîòåíòíîñòè
ϕ(a∧b)=ϕ(a)∧ϕ(b)=ϕ(a)
è
ϕ(a∨b)=ϕ(a)∨ϕ(b)=ϕ(b),
ò.å. îáðàçû îáúåäèíåíèÿ a è b ñîâïàäàþò ñ îáðàçîì a è,
ñëåäîâàòåëüíî, ñ b. Èíûìè ñëîâàìè, ìíîæåñòâî ýëåìåíòîâ èç L,
îòîáðàæàåìûõ ãîìîìîðôèçìîì â îäèí è òîò æå ýëåìåíò â M, âñåãäà
îáðàçóåò ïîäðåøåòêó, (ò.å. a, b îòîáðàæàåòñÿ â îäèí ýëåìåíò âìåñòå
ñ a∧b è a∨b). Íî ýòà ïîäðåøåòêà íå ïðîèçâîëüíà. Íàïðèìåð,
åñëè ðåøåòêà ñîäåðæèò íóëåâîé è åäèíè÷íûé ýëåìåíòû, òî îíè,
î÷åâèäíî, îáðàçóþò ïîäðåøåòêó. Åñëè ýòè ãðàíè÷íûå ýëåìåíòû
ïåðåõîäÿò ïðè ãîìîìîðôèçìå â îäèí è òîò æå ýëåìåíò, òî èõ îáðàç
áóäåò îäíîâðåìåííî è íóëåâûì è åäèíè÷íûì ýëåìåíòîì, à ýòî
îçíà÷àåò, ÷òî îí áóäåò îáðàçîì âñåõ ýëåìåíòîâ. Ñëåäîâàòåëüíî, ýòî
óæå íå áóäåò ðåøåòêà, ñîäåðæàùàÿ õîòÿ áû äâà ýëåìåíòà.
Óòâåðæäåíèå.  îáùåì ñëó÷àå, åñëè a ≤ b è ϕ(a)=ϕ(b), òî
îáðàç ëþáîãî a ≤ x ≤ b áóäåò ñîâïàäàòü ñ ϕ(a) è ϕ(b).
Äåéñòâèòåëüíî, åñëè a ≤ x ≤ b, òî x=x∨a è x=x∧b. Òàê êàê
x=a ∨ (x ∧ b) è ϕ(x)=ϕ(a)∨(ϕ(x)∧ϕ(b)), òî ïðè ϕ(a)=ϕ(b)
ϕ(x)=ϕ(a) ∨ (ϕ(x) ∧ ϕ(a))=ϕ(a) ïî çàêîíó ïîãëîùåíèÿ. Òàêàÿ
ïîäðåøåòêà, êîòîðàÿ ïðè ãîìîìîðôèçìå îòîáðàæàåòñÿ â îäèí è
òîò æå ýëåìåíò, ÿâëÿåòñÿ âûïóêëîé ïîäðåøåòêîé.
Âûïóêëûå ïîäðåøåòêè, êîòîðûå ïðè ãîìîìîðôèçìå ìîãóò
îòîáðàæàòüñÿ â íóëåâîé è åäèíè÷íûé ýëåìåíòû, èãðàþò îñîáåííî
âàæíóþ ðîëü. Íàïðèìåð, åñëè ê ðåøåòêå äîáàâëåí íîâûé ýëåìåíò,
êîòîðûé ìåíüøå âñåõ îñòàëüíûõ, òî îòîáðàçèâ íîâûé ýëåìåíò â
íóëåâîé, ìû ïîëó÷èì òîò æå ãîìîìîðôèçì, ÷òî è ðàíüøå. Åñëè
ýòîò ãîìîìîðôèçì îòîáðàæàåò a â íóëåâîé ýëåìåíò è x ≤ a, òî (òàê
êàê 0≤ x) â ñèëó âûïóêëîñòè, ýëåìåíò x òàêæå ïåðåõîäèò â íóëåâîé
ýëåìåíò.
Ãëàâà 7 Ñòðîåíèå è ïðåäñòàâëåíèå ðåøåòîê

104 105
Ïîäðåøåòêà ðåøåòêè, ñîäåðæàùàÿ âìåñòå ñ ëþáûì ýëåìåíòîì
a âñå ýëåìåíòû x, òàêèå, ÷òî x ≤ a, íàçûâàåòñÿ èäåàëîì ðåøåòêè, à
ïîäðåøåòêà, ñîäåðæàùàÿ âìåñòå ñ ëþáûì ýëåìåíòîì a âñå ýëåìåíòû
x, òàêèå ÷òî a ≤ x, íàçûâàåòñÿ äâîéñòâåííûì èäåàëîì ðåøåòêè, èëè
ôèëüòðîì.
Îïðåäåëåíèå 7.15. Ïîäìíîæåñòâî J ðåøåòêè íàçûâàåòñÿ èäåàëîì,
åñëè
1) J çàìêíóòî îòíîñèòåëüíî îáúåäèíåíèÿ, ò.å. åñëè a∈J è b∈J,
òî è a∨b∈J;
2) Èç a ∈ J è x ≤ a ñëåäóåò, ÷òî x ∈ J (J íåïóñòî).
Îïðåäåëåíèå 7.16. Ïîäìíîæåñòâî D íàçûâàåòñÿ äâîéñòâåííûì
(äóàëüíûì) èäåàëîì, åñëè
1) D çàìêíóòî îòíîñèòåëüíî ïåðåñå÷åíèÿ;
2) Èç b ∈ D è b ≤ y ñëåäóåò, ÷òî y ∈ D (D íå âñÿ ðåøåòêà).
Ëþáîé ýëåìåíò ðåøåòêè îïðåäåëÿåò èäåàë, ñîñòîÿùèé èç
ýëåìåíòîâ, êîòîðûå íå áîëüøå åãî. Íàïðèìåð, åñëè a ≤ c è b ≤ c, òî
a ∨ b ≤ c. Åñëè x ≤ a, òî ïî òðàíçèòèâíîñòè x≤c, à a∧b≤a. Îòñþäà
ñëåäóåò çàìêíóòîñòü îòíîñèòåëüíî îáúåäèíåíèÿ è ïåðåñå÷åíèÿ.
Ïîëó÷åííûé èäåàë îáîçíà÷èì J
c
. Ýëåìåíòû, êîòîðûå íå ìåíåå c,
îáðàçóþò äâîéñòâåííûé èäåàë D
c
.
Ïðèìåð. Íà ðèñ. 7.10 çàäàíî îòîáðàæåíèå ýëåìåíòà c∈L â 0 è
ýëåìåíòà f â I ðåøåòêè 2. Äëÿ òîãî, ÷òîáû ïðîäîëæèòü ýòî
îòîáðàæåíèå äî ãîìîìîðôèçìà, íåîáõîäèìî îòîáðàçèòü ýëåìåíòû
d, b, a â 0, à ýëåìåíò e â I ðåøåòêè 2. Òîãäà ýëåìåíòû {a, b, d,c}
îáðàçóþò èäåàë J
c
, à ýëåìåíòû {f, e} äâîéñòâåííûé èäåàë D
f
. Åñëè
ê ðåøåòêå äîáàâèòü ýëåìåíò h, òî äëÿ ïðîäîëæåíèÿ ãîìîìîðôèçìà
íåîáõîäèìî îòîáðàçèòü ýòîò ýëåìåíò â 0. Ýëåìåíò g íå ïðèíàäëåæèò
íè èäåàëó, íè äâîéñòâåííîìó èäåàëó.
Ìîæíî ïîêàçàòü, ÷òî â êîíå÷íîé ðåøåòêå èìååòñÿ ñòîëüêî
èäåàëîâ è äâîéñòâåííûõ èäåàëîâ, ñêîëüêî îíà ñîäåðæèò ýëåìåíòîâ.
Íà ðèñ. 7.11 äëÿ ðåøåòêè N
5
ïîêàçàíî ïÿòü èäåàëîâ, âêëþ÷àÿ âñþ
ðåøåòêó â öåëîì.
7.5.3. Ïðèìàðíûå èäåàëû
Óñëîâèÿ, îïðåäåëÿþùèå èäåàë è äâîéñòâåííûé èäåàë ðåøåòêè,
äâîéñòâåííû äðóã äðóãó. Ïîýòîìó, åñëè ðåøåòêó L ðàçáèòü íà äâå
÷àñòè A è B òàê, ÷òîáû äëÿ ÷àñòè A âûïîëíÿëîñü óñëîâèå (2)
îïðåäåëåíèÿ èäåàëà: èç a∈A è x ≤ a ñëåäóåò, ÷òî x∈A (A íåïóñòî),
òî äëÿ ÷àñòè B áóäåò âûïîëíÿòüñÿ óñëîâèå (2) äâîéñòâåííîãî èäåàëà.
Òàêèì îáðàçîì, A áóäåò èäåàëîì L, à B äâîéñòâåííûì èäåàëîì, è
ïðè ýòîì A è B áóäóò äîïîëíÿòü äðóã äðóãà äî ïîëíîãî ìíîæåñòâà,
îáðàçóþùåãî ðåøåòêó L.
Óñëîâèå (2) îïðåäåëåíèÿ èäåàëà âûïîëíÿåòñÿ â òîì è òîëüêî
òîì ñëó÷àå, åñëè äëÿ B âûïîëíÿåòñÿ óñëîâèå (2) îïðåäåëåíèÿ
äâîéñòâåííîãî èäåàëà. Äåéñòâèòåëüíî, åñëè (2) âûïîëíÿåòñÿ äëÿ A
è íåêîòîðûé ýëåìåíò b∈B, òî ïðè ó ≤ b ýëåìåíò y íå ìîæåò
ïðèíàäëåæàòü A, òàê êàê òîãäà îíî ñîäåðæàëî áû è b, ñëåäîâàòåëüíî,
y∈B. Ñ äðóãîé ñòîðîíû, åñëè (2) âûïîëíÿåòñÿ äëÿ B è a∈A, òî
âñÿêèé ýëåìåíò x ≤ a ïðèíàäëåæèò A, ïîñêîëüêó â ïðîòèâíîì ñëó÷àå
ýëåìåíò a òàêæå ïðèíàäëåæàë áû è B.
Òàêîå ðàçáèåíèå ðåøåòêè íà ïîäìíîæåñòâà, ÿâëÿþùèåñÿ
äîïîëíåíèÿìè äðóã äðóãà è îáðàçóþùèå èäåàë è äâîéñòâåííûé
èäåàë, íàçûâàþò ñå÷åíèåì ðåøåòêè. Ïîäìíîæåñòâî A íàçûâàþò íèæ-
íèì ñåãìåíòîì, B âåðõíèì ñåãìåíòîì.
 îáùåì ñëó÷àå íèæíèé ñåãìåíò íå ÿâëÿåòñÿ èäåàëîì, à âåðõ-
íèé äâîéñòâåííûì èäåàëîì, òàê êàê îíè ìîãóò áûòü ïóñòûì
ìíîæåñòâîì è âñåé ðåøåòêîé èëè íå óäîâëåòâîðÿòü óñëîâèþ (2).
Íî åñëè íèæíèé ñåãìåíò óäîâëåòâîðÿåò îïðåäåëåíèþ èäåàëà, òî
îí íàçûâàåòñÿ ïðèìàðíûì èäåàëîì, èëè ïðîñòûì èäåàëîì, à âåðõíèé
ñåãìåíò äâîéñòâåííûì, èëè äóàëüíûì ïðèìàðíûì èäåàëîì
(ôèëüòðîì).
Ïðèìàðíûé è äâîéñòâåííûé åìó èäåàëû ìîæíî ïîëó÷èòü,
îïðåäåëèâ ãîìîìîðôèçì f ðåøåòêè L â ðåøåòêó èç äâóõ ýëåìåíòîâ
(â ðåøåòêó 2), ãäå ïîä äåéñòâèåì f â íóëü ïåðåõîäÿò ýëåìåíòû
íèæíåãî ñåãìåíòà, à â åäèíèöó ýëåìåíòû âåðõíåãî ñåãìåíòà,
îáðàçóþùèå äâîéñòâåííûé ïðèìàðíûé èäåàë (ñì. ðèñ. 7.12). Ýòî
îáóñëîâëåíî ñâîéñòâîì ãîìîìîðôèçìà ñîõðàíÿòü óïîðÿäî÷åííîñòü.
Åñëè ýëåìåíòû a è b ïðèíàäëåæàò âåðõíåìó ñåãìåíòó, òî ïåðåñå÷åíèå
èõ a∧b òàêæå ïðèíàäëåæèò âåðõíåìó ñåãìåíòó è îòîáðàæàåòñÿ â
I: f(a ∧ b)=f(a) ∧ f(b)=I ∧ I=I. Åñëè æå a è b ïðèíàäëåæàò
íèæíåìó ñåãìåíòó, òî f(a∨b)=f(a)∨f(b)=0∨0=0, ò.å. èõ
Ãëàâà 7 Ñòðîåíèå è ïðåäñòàâëåíèå ðåøåòîê
Ðèñ. 7.10. Èäåàë
èäâîéñòâåííûé èäåàë.
Ðèñ. 7.11. Èäåàëû ðåøåòêè N
5
.
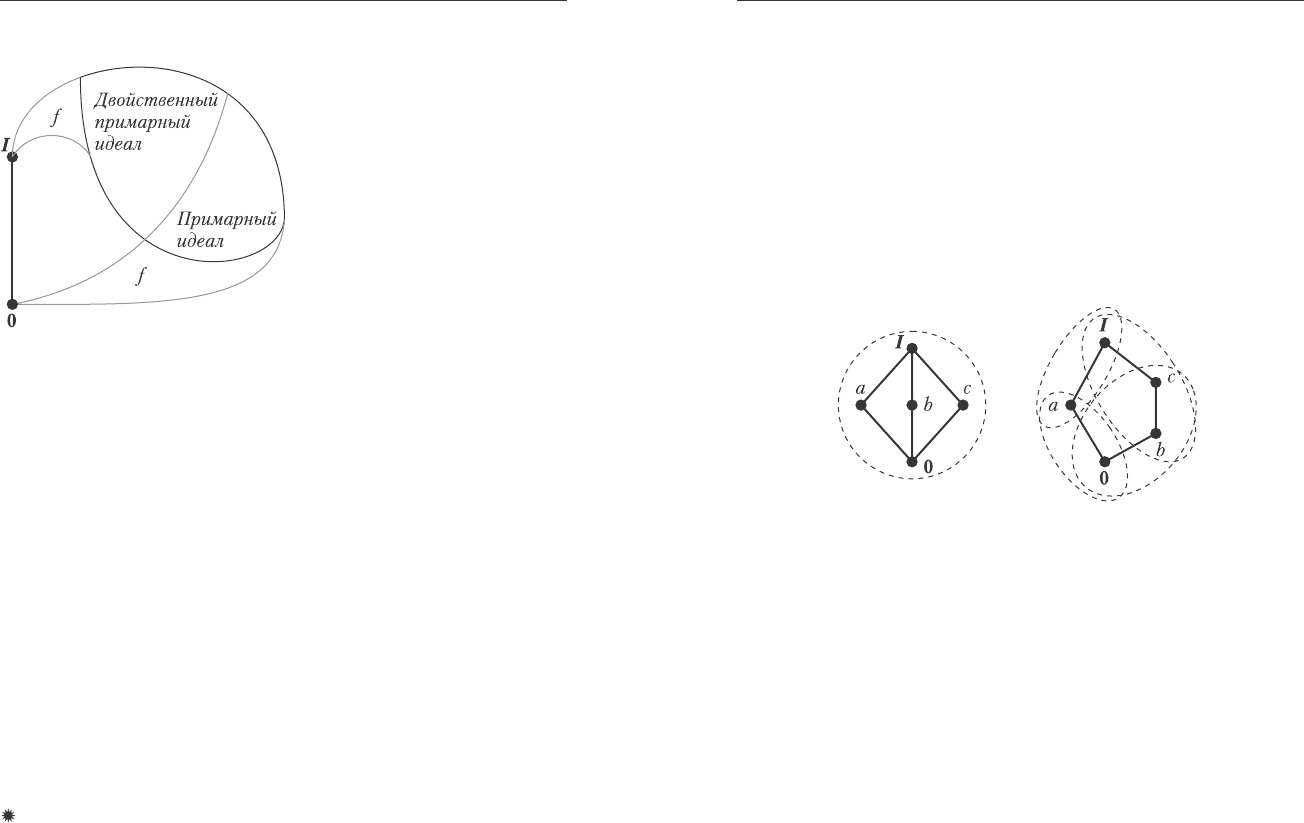
106 107
îáúåäèíåíèå îòîáðàæàåòñÿ â 0. Ñëåäîâàòåëüíî íèæíèé ñåãìåíò
ÿâëÿåòñÿ èäåàëîì, à âåðõíèé äâîéñòâåííûì èäåàëîì.
Ýòî ñâîéñòâî ñåãìåíòîâ
ïîëíîñòüþ îïðåäåëÿåò ïðè-
ìàðíûé èäåàë. Èíà÷å ãîâîðÿ,
ïðèìàðíûé èäåàë ìîæíî
ïîëó÷èòü, ëèøü îòîáðàæàÿ
ðåøåòêó â ðåøåòêó èç äâóõ
ýëåìåíòîâ: ïðèìàðíûé èäåàë
îáðàçóþò ýëåìåíòû, êîòîðûå
ïðè ãîìîìîðôèçìå ïåðåõîäÿò
â íóëåâîé ýëåìåíò. Ðàññìîò-
ðèì íåêîòîðûå ñâîéñòâà
ïðèìàðíûõ èäåàëîâ.
1. Èäåàë J ðåøåòêè ÿâëÿ-
åòñÿ ïðèìàðíûì èäåàëîì òîãäà
è òîëüêî òîãäà, åñëè ïðè
a∧b∈ J ëèáî a ∈ J, ëèáî b ∈ J. Èíûìè ñëîâàìè, åñëè ïåðåñå÷åíèå
êàêèõ-ëèáî äâóõ ýëåìåíòîâ ïðèíàäëåæèò ïðèìàðíîìó èäåàëó, òî â
íåì äîëæåí ñîäåðæàòüñÿ êàêîé-ëèáî èç ýòèõ ýëåìåíòîâ.
Ïðèìàðíûé èäåàë ìîæíî ðàññìàòðèâàòü êàê íèæíþþ
∧-ïîëóðåøåòêó, ñëåäîâàòåëüíî, â íåì ñîäåðæèòñÿ ïåðåñå÷åíèå
êàêèõ-ëèáî ýëåìåíòîâ à è b. Ïðè ýòîì âåðõíÿÿ ïîëóðåøåòêà áóäåò
äâîéñòâåííûì ïðèìàðíûì èäåàëîì, êîòîðûé çàìêíóò îòíîñèòåëüíî
ïåðåñå÷åíèÿ. Òàêèì îáðàçîì, åñëè à è b ïðèíàäëåæàò äâîéñòâåííîìó
èäåàëó D, òî a∧b∈D òàêæå. Ñëåäîâàòåëüíî, åñëè a ∧ b íå ïðèíàä-
ëåæèò D, òî îí íå ñîäåðæèò ëèáî à, ëèáî b, ëèáî à è b âìåñòå.
2. Åñëè äëÿ ýëåìåíòà ðåøåòêè ñóùåñòâóåò äîïîëíåíèå, òî ëþáîé
ïðèìàðíûé èäåàë ñîäåðæèò ëèáî ýëåìåíò, ëèáî åãî äîïîëíåíèå.
Åñëè L ðåøåòêà ñ äîïîëíåíèÿìè, çíà÷èò ýòî ðåøåòêà ñ 0 è I.
0 áóäåò ýëåìåíòîì èäåàëà J, à I äâîéñòâåííîãî èäåàëà D. Åñëè
íåêîòîðûé ýëåìåíò à âìåñòå ñî ñâîèì äîïîëíåíèåì à' ïðèíàäëåæèò
îäíîìó èç èäåàëîâ, òî òàê êàê a∨a'=I, à a ∧ a'=0, òî òàêîé
èäåàë äîëæåí áûòü âñåé ðåøåòêîé. Íî äâîéñòâåííûé èäåàë íå ìîæåò
áûòü âñåé ðåøåòêîé (âñåì ìíîæåñòâîì), à ïðèìàðíûé èäåàë
ïóñòûì ìíîæåñòâîì, ñëåäîâàòåëüíî, ïðèìàðíûé èäåàë ìîæåò
ñîäåðæàòü ëèáî ýëåìåíò, ëèáî åãî äîïîëíåíèå.
Ïðèìåðû.
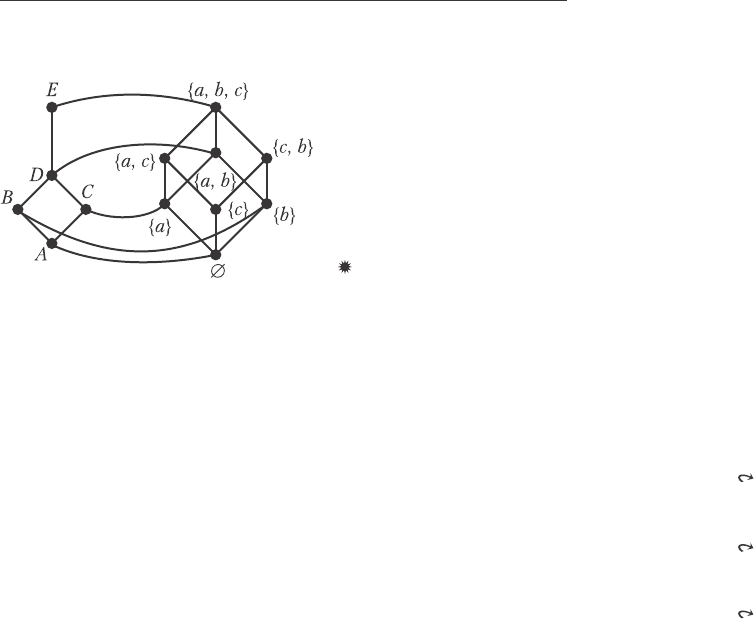
Ðàññìîòðèì èäåàëû è ïðèìàðíûå èäåàëû íåäèñòðèáóòèâíûõ
ðåøåòîê èç ïÿòè ýëåìåíòîâ (ðèñ. 7.13). Êàæäûé èäåàë ñîñòîèò èç
ýëåìåíòîâ, êîòîðûå íå áîëüøå äàííîãî ýëåìåíòà. Ýòîò ýëåìåíò
ÿâëÿåòñÿ îáúåäèíåíèåì âñåõ ýëåìåíòîâ èäåàëà. Ñëåäîâàòåëüíî, â
êàæäîé èç äâóõ ðåøåòîê èç 5 ýëåìåíòîâ ñóùåñòâóåò ïî 5 èäåàëîâ.
Ðèñ. 7. 12. Ñå÷åíèå ðåøåòêè
Ðàññìîòðèì ðèñ. 7.13, a. Èç ýëåìåíòîâ à, b, c ïî êðàéíåé ìåðå äâà
ïðèíàäëåæàò ëèáî J, ëèáî D. Äîïóñòèì, a, b ∈ J. Åñëè a ∈ J, òî
ëþáîé ýëåìåíò x ≤ a òàêæå ïðèíàäëåæèò J, ò.å. 0 ∈ J . Âìåñòå ñ a, b
èõ îáúåäèíåíèå ïðèíàäëåæèò J, ò.å. a ∨ b= I∈J. Ñ äðóãîé ñòîðîíû,
ýëåìåíò c∈ J, òàê êàê c≤I. Ñëåäîâàòåëüíî, ñóùåñòâóåò òîëüêî îäèí
ïðèìàðíûé èäåàë, ñîâïàäàþùèé ñî âñåé ðåøåòêîé.
Âî âòîðîé ðåøåòêå (ðèñ. 7.13, b) ñóùåñòâóþò äâà ïðèìàðíûõ èäåàëà:
[0, a], è [0, b, c].
Ðàññìîòðèì [0,a]. 0 ∨ a=a,0 ∧ a=0. Äëÿ à ñóùåñòâóåò åäèí-
ñòâåííûé ýëåìåíò 0 ≤ a, ñëåäîâàòåëüíî [0,a] ïðèìàðíûé èäåàë.
Ðàññìîòðèì [0,b,c]. 0 ∨ b=b,0 ∧ b=0, b ∨ c=c, b ∧ c=b. Äðóãèõ
ýëåìåíòîâ, ìåíüøèõ b è c íåò, êðîìå íóëÿ, ñëåäîâàòåëüíî, [0, c]
ïðèìàðíûé èäåàë.
Ðèñ. 7.13. Ïðèìàðíûå èäåàëû.
Íàèáîëåå «åñòåñòâåííûì» ïðåäñòàâëåíèåì ðåøåòêè ÿâëÿåòñÿ,
íàâåðíîå, äèñòðèáóòèâíàÿ áóëåâà ðåøåòêà ìíîæåñòâà-ñòåïåíè, ò.å.
ìíîæåñòâà âñåõ ïîäìíîæåñòâ íåêîòîðîãî ìíîæåñòâà, óïîðÿäî-
÷åííîãî îòíîøåíèåì âêëþ÷åíèÿ. Äëÿ ìíîæåñòâà èç òðåõ ýëåìåíòîâ
ýòî áóëåâ ãèïåðêóá (áóëåâà ðåøåòêà 2
3
), â êîòîðîì îïåðàöèè
îáúåäèíåíèÿ è ïåðåñå÷åíèÿ ñîâïàäàþò ñ èõ òåîðåòèêî-ìíîæå-
ñòâåííûìè èíòåðïðåòàöèÿìè. Î÷åâèäíî, áûëî áû ïîëåçíî íàó÷èòü-
ñÿ ñòðîèòü ãîìîìîðôèçì, îòîáðàæàþùèé çàäàííóþ ðåøåòêó â
ðåøåòêó ïîäìíîæåñòâ íåêîòîðîãî ìíîæåñòâà òàê, ÷òîáû ðàçëè÷íûå
ýëåìåíòû èñõîäíîé ðåøåòêè ïåðåõîäèëè áû â ðàçëè÷íûå ïîäìíî-
æåñòâà, ò.å. ñòðîèòü ìîíîìîðôèçì. Îäíàêî òàêîãî óíèâåðñàëüíîãî
ãîìîìîðôèçìà íå ñóùåñòâóåò, òàê êàê ðåøåòêà ïîäìíîæåñòâ ëþáîãî
ìíîæåñòâà äèñòðèáóòèâíà, è, ñëåäîâàòåëüíî, ìîæåò ñëóæèòü ïðåä-
ñòàâëåíèåì òîëüêî äèñòðèáóòèâíûõ ðåøåòîê, äëÿ êîòîðûõ äàííàÿ
çàäà÷à ðàçðåøèìà. Äåéñòâèòåëüíî, ëþáóþ äèñòðèáóòèâíóþ ðåøåòêó
ìîæíî ïðåäñòàâèòü íåêîòîðîé ïîäðåøåòêîé ïîäìíîæåñòâ îïðåäå-
ëåííûì îáðàçîì âûáðàííîãî ìíîæåñòâà. Ýòîò ðåçóëüòàò èçâåñòåí
a) b)
Ãëàâà 7 Ñòðîåíèå è ïðåäñòàâëåíèå ðåøåòîê
108
ïîä íàçâàíèåì òåîðåìû Ñòîóíà, êîòîðóþ ìû çäåñü ïðèâåäåì áåç
äîêàçàòåëüñòâà.
Òåîðåìà 7.7 (Ñòîóíà î
ïðåäñòàâëåíèè). Äëÿ ëþáîé
äèñòðèáóòèâíîé ðåøåòêè
ñóùåñòâóåò ìîíîìîðôèçì,
îòîáðàæàþùèé åå â ðåøåòêó
âñåõ ïîäìíîæåñòâ íåêîòî-
ðîãî ìíîæåñòâà, ïðè÷åì òàê,
÷òî äîïîëíåíèå ïåðåõîäèò â
äîïîëíåíèå.
Ïðèìåð. Íà ðèñ.7.14 ïî-
êàçàí ìîíîìîðôèçì ðåøåò-
êè â ðåøåòêó ïîäìíîæåñòâ
ìíîæåñòâà A ={a, b, c}.
Ðèñ. 7.14. Ê òåîðåìå Ñòîóíà.
Ãëàâà 7
Ãëàâà 8. ÃÐÀÔÛ
8.1. Îñíîâíûå ïîíÿòèÿ è îïðåäåëåíèÿ
Ñ ïîíÿòèåì ãðàôà îáû÷íî ñâÿçûâàåòñÿ åãî ãðàôè÷åñêîå
ïðåäñòàâëåíèå, ïðè êîòîðîì îí èçîáðàæàåòñÿ êàê ìíîæåñòâî òî÷åê,
íåêîòîðûå èç êîòîðûõ ñîåäèíåíû ëèíèÿìè. Îäíàêî ãðàô îòëè÷àåòñÿ
îò ãåîìåòðè÷åñêèõ êîíôèãóðàöèé (ñêàæåì, ôèãóð, êîòîðûå òàêæå
ñîñòîÿò èç òî÷åê-âåðøèí è ëèíèé-ñòîðîí) òåì, ÷òî â ãðàôå íåñóùå-
ñòâåííû ðàññòîÿíèÿ ìåæäó òî÷êàìè, ôîðìà ñîåäèíÿþùèõ ëèíèé è
óãëû ìåæäó íèìè. Âàæíî ëèøü, ñîåäèíåíà ëè äàííàÿ ïàðà òî÷åê
ëèíèåé, èëè íåò. Ïîýòîìó ãðàô èíîãäà íàçûâàþò òîïîëîãè÷åñêèì
îáúåêòîì, ò.å.îáúåêòîì, ñâîéñòâà êîòîðîãî íå èçìåíÿþòñÿ ïðè
ðàñòÿãèâàíèè, ñæàòèè, èñêðèâëåíèè (íî áåç ðàçðûâîâ è ñêëåèâà-
íèé). Ïî ýòîé æå ïðè÷èíå (âàæíî ëèøü íàëè÷èå èëè îòñóòñòâèå
ñîåäèíåíèÿ) ãðàô îáúåêò äèñêðåòíûé è ìîæåò áûòü çàäàí äâóìÿ
äèñêðåòíûìè ìíîæåñòâàìè: ìíîæåñòâîì òî÷åê, êîòîðûå áóäåì
íàçûâàòü âåðøèíàìè, è ìíîæåñòâîì ëèíèé, ñîåäèíÿþùèõ íåêîòîðûå
âåðøèíû. Ëèíèè áóäåì íàçûâàòü ðåáðàìè.
Ñóùåñòâóþò äâà îñíîâíûõ âèäà ãðàôîâ îðèåíòèðîâàííûå, â
êîòîðûõ ëèíèè èìåþò íàïðàâëåíèå îò îäíîé âåðøèíû ê äðóãîé, è
íåîðèåíòèðîâàííûå, â êîòîðûõ ëèíèè íå èìåþò íàïðàâëåíèÿ.
Îïðåäåëåíèå 8.1. Íåîðèåíòèðîâàííûì ãðàôîì G =(V, E)
íàçûâàåòñÿ îáúåêò, çàäàííûé ïàðîé ìíîæåñòâ (V, E), ãäå V
ìíîæåñòâî âåðøèí, E ⊆V×V ìíîæåñòâî ðåáåð.
Îïðåäåëåíèå 8.2. Îðèåíòèðîâàííûì ãðàôîì (îðãðàôîì)
íàçûâàåòñÿ ãðàô D=(V,E), ãäå V ìíîæåñòâî âåðøèí,
E⊆V×V ìíîæåñòâî îðèåíòèðîâàííûõ ðåáåð, èëè äóã.
Îïðåäåëåíèå 8.3. Ãðàô íàçûâàåòñÿ ïðîñòûì, åñëè êàæäóþ ïàðó
âåðøèí ñîåäèíÿåò íå áîëåå, ÷åì îäíî ðåáðî. Ãðàô íàçûâàåòñÿ
ìóëüòèãðàôîì, åñëè õîòÿ áû îäíó ïàðó âåðøèí ñîåäèíÿåò áîëåå,
÷åì îäíî ðåáðî. Ðåáðà ìóëüòèãðàôà, ñîåäèíÿþùèå îäíó è òó æå
ïàðó âåðøèí, íàçûâàþòñÿ êðàòíûìè.
 ïðîñòîì ãðàôå ðåáðî îäíîçíà÷íî îïðåäåëÿåòñÿ ïàðîé âåðøèí,
êîòîðûå îíî ñîåäèíÿåò. Â íåîðèåíòèðîâàííîì ãðàôå ïîðÿäîê
âåðøèí â ïàðå íå âàæåí, ïîýòîìó ðåáðà ïðîñòîãî íåîðèåíòèðî-
âàííîãî ãðàôà îïðåäåëÿþòñÿ êàê ìíîæåñòâî íåóïîðÿäî÷åííûõ ïàð
âåðøèí (v
i
,v
j
)∈V×V.  îðèåíòèðîâàííîì ãðàôå óïîðÿäî÷åííàÿ
ïàðà (v
i
,v
j
)∈V×V óêàçûâàåò íàïðàâëåíèå äóãè: îò âåðøèíû v
i
ê
âåðøèíå v
j
. Îíà èìååò íà÷àëî (âåðøèíó v
i
, èç êîòîðîé äóãà âûõîäèò)
è êîíåö (âåðøèíó v
j
, â êîòîðóþ îíà çàõîäèò). Â ìóëüòèãðàôå êàæäîå
ðåáðî äîëæíî èìåòü ñâîå ñîáñòâåííîå èìÿ. Âåðøèíû, ñîåäèíÿåìûå
110 111Ãëàâà 8 Ãðàôû
Îòíîøåíèå ñìåæíîñòè â íåîðèåíòèðîâàííîì ãðàôå âñåãäà
ñèììåòðè÷íî, ïîñêîëüêó ïîðÿäîê âåðøèí â ïàðå (v
i
,v
j
) íå âàæåí.
Íàëè÷èå ðåôëåêñèâíîñòè è òðàíçèòèâíîñòè çàâèñèò îò êîíêðåòíûõ
ñâîéñòâ ãðàôà. Ìàòðèöà ñìåæíîñòè ïóñòîãî ãðàôà çàïîëíåíà òîëüêî
íóëÿìè, à ìàòðèöà ñìåæíîñòè ïîëíîãî ãðàôà ñ ïåòëÿìè òîëüêî
åäèíèöàìè. Äëÿ ìóëüòèãðàôà ìàòðèöà ñìåæíîñòè óæå íå ÿâëÿåòñÿ
áèíàðíîé: â íåé a
ij
= k, ãäå k ÷èñëî êðàòíûõ ðåáåð, ñîåäèíÿþùèõ
âåðøèíû v
i
è v
j
.
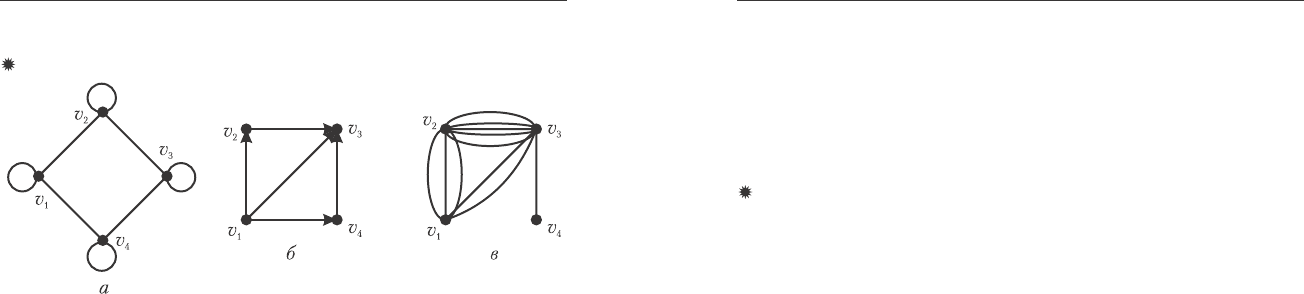
Ïðèìåðû.
Ìàòðèöû ñìåæíîñòè äëÿ ãðàôîâ, ïðèâåäåííûõ íà ðèñ. 8.1.
A (G) =
1101
1110
0111
1011
, A (D) =
0111
0010
0000
0010
, A (M) =
0320
3040
2401
0010
.
8.2.2. Ìàòðèöà èíöèäåíòíîñòè
Èíöèäåíòíîñòü ýòî îòíîøåíèå ìåæäó âåðøèíàìè è ðåáðàìè:
ðåáðî èíöèäåíòíî êàæäîé èç âåðøèí, êîòîðîå îíî ñîåäèíÿåò. Îíî
çàäàåòñÿ ìàòðèöåé èíöèäåíòíîñòè C, â êîòîðîé ñòðîêè ïîìå÷àþòñÿ
èìåíàìè âåðøèí, à ñòîëáöû èìåíàìè ðåáåð ãðàôà. Ìàòðèöà
èíöèäåíòíîñòè ãðàôà îïðåäåëÿåòñÿ êàê (n × m)ìàòðèöà
C(G)=(c
ij
), ó êîòîðîé
1, åñëè âåðøèíà èíöèäåíòíà ðåáðó ,
0, åñëè âåðøèíà íå èíöèäåíòíà ðåáðó .
ij
ij
ij
ve
c
ve
=
Ýòî ïðÿìîóãîëüíàÿ áèíàðíàÿ ìàòðèöà, â êîòîðîé ÷èñëî ñòðîê
ðàâíî ÷èñëó âåðøèí ãðàôà n, à ÷èñëî ñòîëáöîâ ÷èñëó ðåáåð m.
×èñëî ðåáåð, èíöèäåíòíûõ âåðøèíå v
i
ãðàôà (îðãðàôà, ìóëüòè-
ãðàôà), íàçûâàåòñÿ ñòåïåíüþ ýòîé âåðøèíû è îáîçíà÷àåòñÿ deg (v
i
).
Ñòåïåíü âåðøèíû ìîæíî îïðåäåëèòü ïî ìàòðèöàì èíöèäåíòíîñòè
è ñìåæíîñòè. Ñòåïåíü âåðøèíû v
i
ðàâíà ÷èñëó åäèíèö â i-é ñòðîêå
ìàòðèöû èíöèäåíòíîñòè èëè ìàòðèöû ñìåæíîñòè.
Ñóììà ñòåïåíåé âñåõ âåðøèí ðàâíà óäâîåííîìó ÷èñëó ðåáåð,
ïîñêîëüêó êàæäîå ðåáðî ó÷àñòâóåò â ñòåïåíÿõ äâóõ âåðøèí,
ò.å.ñ÷èòàåòñÿ â ýòîé ñóììå äâà ðàçà. Ïîñêîëüêó ýòà ñóììà ÷åòíà,
òî è ÷èñëî âåðøèí ñ íå÷åòíûìè ñòåïåíÿìè òîæå ÷åòíî.
Âåðøèíà, ñòåïåíü êîòîðîé ðàâíà 1, íàçûâàåòñÿ êîíöåâîé, èëè âèñÿ÷åé.
Ãðàô íàçûâàåòñÿ îäíîðîäíûì ñòåïåíè k, åñëè ñòåïåíè âñåõ åãî
âåðøèí ðàâíû k.
ðåáðîì, íå îáÿçàòåëüíî ðàçëè÷íû. Ðåáðî, ñîåäèíÿþùåå âåðøèíó v
i
ñ ñàìîé ñîáîé, ò.å.ïàðà (v
i
, v
i
), íàçûâàåòñÿ ïåòëåé.
Ïðèìåðû.
Ðèñ. 8.1. Ïðèìåðû ãðàôîâ:
à) ïðîñòîé íåîðèåíòèðîâàííûé ãðàô ñ ïåòëÿìè G;
á) îðèåíòèðîâàííûé ãðàô D;
â) íåîðèåíòèðîâàííûé ìóëüòèãðàô M.
Ãðàô ìîæåò âîâñå íå èìåòü ðåáåð: E = ∅. Òàêîé ãðàô íàçûâàåòñÿ
ïóñòûì, èëè 0ãðàôîì.
Äëÿ ïðîñòîãî ãðàôà ñóùåñòâóåò äðóãîé êðàéíèé ñëó÷àé, êîãäà
âñå âåðøèíû ñîåäèíåíû ìåæäó ñîáîé ðåáðàìè. Òàêîé ãðàô íàçû-
âàåòñÿ ïîëíûì, ïðè÷åì ðàçëè÷àþò äâà âèäà ïîëíûõ ãðàôîâ ñ
ïåòëÿìè è áåç ïåòåëü. Ïîëíûé ãðàô ñ n âåðøèíàìè èìååò
(n
2
n)/2
ðå-
áåð (÷èñëî ñî÷åòàíèé èç n ïî 2), åñëè ïåòëè íå ó÷èòûâàþòñÿ, è
(n
2
n)/2 + n = (n
2
+ n)/2ðåáåð, åñëè äîáàâèòü n ïåòåëü. Ïîëíûé
ãðàô ñ n âåðøèíàìè áåç ïåòåëü îáîçíà÷àåòñÿ K
n
. Ïîíÿòíî, ÷òî â
ìóëüòèãðàôå îãðàíè÷åíèé íà ÷èñëî ðåáåð íåò.
8.2. Íåîðèåíòèðîâàííûå ãðàôû
8.2.1. Ìàòðèöà ñìåæíîñòè
Íåîðèåíòèðîâàííûé ãðàô çàäàåò äâà îòíîøåíèÿ ìåæäó ñâîèìè
ýëåìåíòàìè: îòíîøåíèå ñìåæíîñòè è îòíîøåíèå èíöèäåíòíîñòè.
Ñìåæíîñòü îòíîøåíèå ìåæäó âåðøèíàìè: äâå âåðøèíû
íàçûâàþòñÿ ñìåæíûìè, åñëè îíè ñîåäèíåíû ðåáðîì. Ýòî
îòíîøåíèå îáû÷íîå áèíàðíîå îòíîøåíèå íà ìíîæåñòâå V, êîòîðîå
äëÿ ïðîñòîãî ãðàôà ìîæåò áûòü çàäàíî êâàäðàòíîé áèíàðíîé
(ò.å.ñîñòîÿùåé èç íóëåé è åäèíèö) ìàòðèöåé ñìåæíîñòè
A(G)=(a
ij
), êîòîðàÿ îïðåäåëÿåòñÿ ñëåäóþùèì îáðàçîì:
1, åñëè ( , ) ,
0, åñëè ( , ) .
ij
ij
ij
uu E
a
uu E
∈
=
∉

112 113
Îïðåäåëåíèå 8.4. Ãðàô G′=(V′, E′) íàçûâàåòñÿ ÷àñòüþ ãðàôà
G=(V, E), åñëè V′⊆ V, à E′ - ïîäìíîæåñòâî ìíîæåñòâà âñåõ
ðåáåð G, îáà êîíöà êîòîðûõ ïðèíàäëåæàò V′.
Îïðåäåëåíèå 8.5. Ãðàô G′=(V′, E′) íàçûâàåòñÿ ïîäãðàôîì ãðàôà
G=(V, E), åñëè V′⊂V, à E′ ìíîæåñòâî âñåõ ðåáåð G, îáà êîíöà
êîòîðûõ ïðèíàäëåæàò V′. Ìíîæåñòâî âåðøèí V′⊂V íàçûâàþò
ïîðîæäàþùèì ìíîæåñòâîì ïîäãðàôà V′, à ñàì ïîäãðàô
ïîðîæäåííûì âåðøèíàìè V′.
Âñÿêèé ïîäãðàô ãðàôà G ÿâëÿåòñÿ ÷àñòüþ G, íî íå âñÿêàÿ ÷àñòü
ïîäãðàô (ñì. ðèñ.8.2). Ïîäãðàô ïîëíîñòüþ îïðåäåëÿåòñÿ ìíîæåñòâîì
V′ ñâîèõ âåðøèí è ìîæåò áûòü ïîñòðîåí òàê: â èñõîäíîì ãðàôå G
âûáèðàåì ìíîæåñòâî âåðøèí V′ è óäàëÿåì âñå ðåáðà, õîòÿ áû îäèí
êîíåö êîòîðûõ íå ïðèíàäëåæèò V′. ×àñòü ãðàôà ýòî ïîäãðàô, èç
êîòîðîãî, âîçìîæíî, óäàëåíû íåêîòîðûå ðåáðà. Íàïðèìåð, ÷àñòü ãðàôà
G íà ðèñ. 8.2, á ñîäåðæèò âåðøèíû v
3
,v
4
, v
5
, v
6
, íî íå ñîäåðæèò ðåáåð
(v
3
,v
4
), (v
4
,v
5
), (v
5
,v
6
), (v
3
,v
6
), â òî âðåìÿ, êàê åãî ïîäãðàô íà ðèñ. 8.2,
â ñîäåðæèò âñå ðåáðà, ñîåäèíÿþùèå ýòè âåðøèíû.
Îïðåäåëåíèå 8.6. ×àñòü ãðàôà, îáðàçîâàííàÿ âåðøèíîé v
i
è âñåìè
âåðøèíàìè, ñìåæíûìè ñ íåé, íàçûâàåòñÿ çâåçäîé âåðøèíû v
i
.
Îïðåäåëåíèå 8.7. Ïîëíûé ïîäãðàô, ïîðîæäåííûé çàäàííûì
ìíîæåñòâîì âåðøèí, íàçûâàåòñÿ êëèêîé.
Ïðèìåð.
Ðèñ.8.2.
a) Ãðàô G; á) ×àñòü ãðàôà G;
â) Ïîäãðàô ãðàôà G, êëèêà; ã) Çâåçäà âåðøèíû v
3
.
Îïðåäåëåíèå 8.8. Ïîäãðàô G′ ãðàôà G íàçûâàåòñÿ ìàêñèìàëüíûì
ïî íåêîòîðîìó ñâîéñòâó, åñëè G′ îáëàäàåò ýòèì ñâîéñòâîì, à
ëþáîé ïîäãðàô ãðàôà G, ñîäåðæàùèé G′, íå îáëàäàåò
èì.Ïîäãðàô G′ ãðàôà G íàçûâàåòñÿ ìèíèìàëüíûì ïî íåêîòîðîìó
ñâîéñòâó, åñëè G′ îáëàäàåò ýòèì ñâîéñòâîì, à ëþáîé ïîäãðàô
ãðàôà G, ñîäåðæàùèéñÿ â G′, íå îáëàäàåò èì.
Íàïðèìåð, ïîäãðàô íà ðèñ. 8.2, â ÿâëÿåòñÿ ìàêñèìàëüíîé êëè-
êîé; ïîäãðàô ýòîãî ïîäãðàôà, ïîðîæäåííûé âåðøèíàìè v
3
,v
4
, v
5
,
òàêæå áóäåò êëèêîé, íî íå ìàêñèìàëüíîé, à ìèíèìàëüíîé êëèêîé
áóäåò ïîäãðàô, ïîðîæäåííûé äâóìÿ âåðøèíàìè, íàïðèìåð, v
3
èv
4
.
Ãëàâà 8 Ãðàôû
8.3. Îðèåíòèðîâàííûå ãðàôû
Äëÿ îðãðàôà åãî áèíàðíàÿ ìàòðèöà ñìåæíîñòè A â îáùåì ñëó÷àå
íåñèììåòðè÷íà: ýëåìåíò a
ij
=1, åñëè è òîëüêî åñëè èìååòñÿ äóãà
e=(v
i
, v
j
). ×èñëî åäèíèö â ýòîé ìàòðèöå ðàâíî ÷èñëó äóã ãðàôà.
(Çàìåòèì, ÷òî â ìàòðèöå ñìåæíîñòè íåîðèåíòèðîâàííîãî ãðàôà
ïåòëå ñîîòâåòñòâóåò îäíà åäèíèöà, ñòîÿùàÿ íà ãëàâíîé äèàãîíàëè,
à îñòàëüíûì ðåáðàì ïî äâå åäèíèöû, ñîîòâåòñòâóþùèå ýëåìåíòàì,
ñèììåòðè÷íûì îòíîñèòåëüíî ãëàâíîé äèàãîíàëè.) Åñëè æå ìàòðèöà
ñìåæíîñòè îðãðàôà D îêàçûâàåòñÿ ñèììåòðè÷íîé, òî ýòî îçíà÷àåò,
÷òî äëÿ êàæäîé äóãè (v
i
, v
j
) â íåì èìååòñÿ ïðîòèâîïîëîæíî
íàïðàâëåííàÿ äóãà (v
j
, v
i
). Òàêàÿ ìàòðèöà ñîâïàäàåò ñ ìàòðèöåé
ñìåæíîñòè íåîðèåíòèðîâàííîãî ãðàôà, ïîëó÷åííîãî èç D çàìåíîé
êàæäîé ïàðû ïðîòèâîïîëîæíî îðèåíòèðîâàííûõ äóã (v
i
, v
j
) è (v
j
,v
i
)
íà îäíî íåîðèåíòèðîâàííîå ðåáðî (v
i
, v
j
). Ïîýòîìó ñèììåòðè÷íûé
îðãðàô âñåãäà ìîæíî çàìåíèòü ïðîñòûì íåîðèåíòèðîâàííûì
ãðàôîì, èìåþùèì òó æå ìàòðèöó ñìåæíîñòè. Îäíàêî ñâîéñòâî
ñèììåòðè÷íîñòè ìîæåò âûïîëíÿòüñÿ íå äëÿ âñåõ äóã îðãðàôà; òîãäà
íà ðèñóíêå èçîáðàæàþòñÿ îáå ïðîòèâîïîëîæíî íàïðàâëåííûå äóãè.
Ïîíÿòèå èíöèäåíòíîñòè äëÿ îðãðàôîâ ñîõðàíÿåòñÿ, îäíàêî â
ìàòðèöå èíöèäåíòíîñòè C ðàçëè÷àþò íà÷àëî è êîíåö äóãè.
Ìàòðèöåé èíöèäåíòíîñòè îðãðàôà D íàçûâàåòñÿ (n × m)
ìàòðèöà Ñ (D)=(ñ
ij
), ó êîòîðîé
1, åñëè âåðøèíà ÿâëÿåòñÿ êîíöîì ä
ó
ãè ,
1, åñëè âåðøèíà ÿâëÿåòñÿ íà÷àëîì ä
ó
ãè ,
0, åñëè âåðøèíà íå èíöèäåíòíà ä
ó
ãå .
ii
ij i i
ii
ve
cv e
ve
=−
Ïðèìåð.
Ðèñ. 8.3. Îðãðàô è åãî ìàòðèöà èíöèäåíòíîñòè.
 êàæäîì ñòîëáöå ìàòðèöû èíöèäåíòíîñòè íàõîäèòñÿ ðîâíî
äâå åäèíèöû: 1è 1. Âåðøèíà v
6
íà ðèñ. 8.3. èìååò ïåòëþ. ×òîáû
1234567
1
2
3
4
5
6
7
1000000
1 100000
011 1000
()
00 11 100
0000100
00000 11
000001 1
xxxxxxx
v
v
v
CD
v
v
v
v
−
−
−
=
−−
−
−
114 115Ãëàâà 8 Ãðàôû
îòîáðàçèòü åå â ìàòðèöå èíöèäåíòíîñòè, ââîäèòñÿ äîïîëíèòåëüíàÿ
ôèêòèâíàÿ âåðøèíà v
7
è ïåòëÿ äåëèòñÿ íà äâå äóãè: x
6
è x
7
.
Íåîáõîäèìîñòü ó÷èòûâàòü îðèåíòàöèþ äóã â îðãðàôå ïðèâîäèò ê
ðàñùåïëåíèþ ïîíÿòèÿ «ñòåïåíü âåðøèíû» íà äâå ÷àñòè. Ïîëóñòåïåíüþ
çàõîäà deg
+
(v
i
) âåðøèíû v
i
íàçûâàåòñÿ ÷èñëî äóã, âõîäÿùèõ â v
i
;
ïîëóñòåïåíüþ èñõîäà deg
(v
i
) ÷èñëî äóã, âûõîäÿùèõ èç íåå.
Ïîëóñòåïåíü èñõîäà v
i
ðàâíà ÷èñëó åäèíèö â i-é ñòðîêå ìàòðèöû
ñìåæíîñòè, ïîëóñòåïåíü çàõîäà v
i
÷èñëó åäèíèö â i-ì ñòîëáöå ìàòðèöû
ñìåæíîñòè. Ïîëóñòåïåíè çàõîäà è èñõîäà ëåãêî îïðåäåëÿþòñÿ è ïî
ìàòðèöå èíöèäåíòíîñòè: ñóììà ïîëîæèòåëüíûõ åäèíèö â i-é ñòðîêå
îïðåäåëÿåò ïîëóñòåïåíü çàõîäà âåðøèíû v
i
, à îòðèöàòåëüíûõ èñõîäà.
Îáùàÿ ñóììà äàåò ñòåïåíü âåðøèíû: deg (v
i
)=deg
+
(v
i
)+deg
(v
i
).
Ïîíÿòèå ïîäãðàôà äëÿ îðãðàôà îñòàåòñÿ òåì æå. Ïîíÿòèå çâåçäû,
êàê è ñòåïåíü, ðàñùåïëÿåòñÿ íà äâå ÷àñòè. Ïîëóçâåçäà çàõîäà âåðøè-
íû v
i
ýòî ïîäãðàô, îïðåäåëÿåìûé âåðøèíîé v
i
è âñåìè âåðøèíàìè,
èç êîòîðûõ äóãè çàõîäÿò â âåðøèíó v
i
. Ïîëóçâåçäà èñõîäà âåðøèíû
v
i
ýòî ïîäãðàô, îïðåäåëÿåìûé âåðøèíîé v
i
è âñåìè âåðøèíàìè, â
êîòîðûå èç v
i
èäóò äóãè.
Ïðèìåð.
Ðèñ. 8.4.
à) îðèåíòèðîâàííûé ãðàô D; á) ÷àñòü ãðàôà D;
â) ïîäãðàô ãðàôà D, ïîðîæäåííûé âåðøèíàìè v
1
, v
2
, v
3
;
ã) ïîëóçâåçäà èñõîäà âåðøèíû v
1
.
Èòàê, ãðàôû è îðãðàôû ìîãóò áûòü çàäàíû òðåìÿ ñïîñîáàìè:
• íåïîñðåäñòâåííûì çàäàíèåì ìíîæåñòâ âåðøèí V è äóã E
(íàïðèìåð, ñïèñêîì);
• ìàòðèöåé ñìåæíîñòè èëè ìàòðèöåé èíöèäåíòíîñòè (ïðàâäà,
ìóëüòèãðàô ìàòðèöåé ñìåæíîñòè íå ìîæåò áûòü çàäàí îäíîçíà÷íî,
ïîñêîëüêó ýòà ìàòðèöà íå ñîäåðæèò èìåí ðåáåð);
• ðèñóíêîì (ñì. ïðèìåðû).
Êîãäà äâà ãðàôà îäèíàêîâû? Äëÿ ïåðâûõ äâóõ ñïîñîáîâ çàäàíèÿ
îòâåò ïðîñò: êîãäà ñîâïàäàþò èõ îïèñàíèÿ ñïèñêè âåðøèí è ðåáåð
èëè ìàòðèöû. Âèçóàëüíî, ïî ðèñóíêó, îïðåäåëèòü, îäèíàêîâû ëè
ãðàôû, ñëîæíåå. Îäèí è òîò æå ãðàô ìîæíî èçîáðàçèòü ðàçíûìè
ðèñóíêàìè, ïî-ðàçíîìó ðàñïîëîæèâ âåðøèíû è ïðèäàâ ðåáðàì ðàç-
íóþ ãåîìåòðè÷åñêóþ ôîðìó è äëèíó.
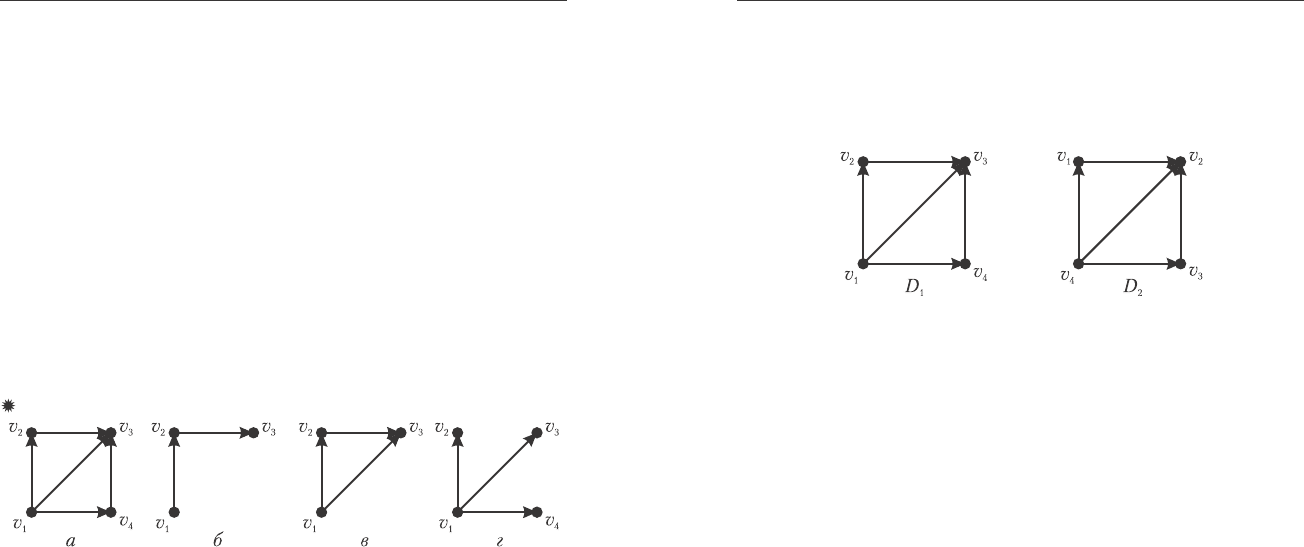
Íàïðèìåð, ãðàôû D
1
è D
2
íà ðèñ. 8.5ãåîìåòðè÷åñêè îäèíàêîâû.
Îäíàêî îíè îòëè÷àþòñÿ íóìåðàöèåé âåðøèí, èç-çà ÷åãî ìàòðèöû
ñìåæíîñòè è ñïèñêè äóã ó íèõ áóäóò ðàçëè÷íû. Íàïðèìåð, äóãà
(v
1
, v
3
) åñòü â ïåðâîì ãðàôå, íî îòñóòñòâóåò âî âòîðîì: âìåñòî íåãî
ïîÿâèëàñü äóãà (v
4
, v
2
). Ïîýòîìó ìíîæåñòâà äóã ýòèõ ãðàôîâ
ðàçëè÷íû è, ñîãëàñíî îïðåäåëåíèþ 8.2, ðàçëè÷íû ñàìè ãðàôû.
Ðèñ. 8.5. Èçîìîðôèçì ãðàôîâ.
Ãðàôû, êîòîðûå îòëè÷àþòñÿ òîëüêî íóìåðàöèåé âåðøèí (è
êîòîðûå, ñëåäîâàòåëüíî, ïðè íåêîòîðîé äðóãîé íóìåðàöèè ìîæíî
ñäåëàòü îäèíàêîâûìè), íàçûâàþòñÿ èçîìîðôíûìè. Èçîìîðôèçì
ãðàôîâ ñ íåáîëüøèì ÷èñëîì âåðøèí èíîãäà ìîæíî íåïîñðåäñòâåííî
óâèäåòü íà ðèñóíêå, îäíàêî, â îáùåì ñëó÷àå ïðîáëåìà óñòàíîâëåíèÿ
èçîìîðôèçìà ãðàôîâ îêàçûâàåòñÿ ñëîæíîé â âû÷èñëèòåëüíîì
îòíîøåíèè çàäà÷åé.
8.4. Ãðàôû è áèíàðíûå îòíîøåíèÿ
Ìåæäó ïðîñòûìè (áåç êðàòíûõ ðåáåð) ãðàôàìè è áèíàðíûìè
îòíîøåíèÿìè ñóùåñòâóåò âçàèìíî îäíîçíà÷íîå ñîîòâåòñòâèå. Âñÿ-
êèé ãðàô ñ ìíîæåñòâîì âåðøèí V = {v
1
,...,v
n
} îïðåäåëÿåò áèíàðíîå
îòíîøåíèå íà ìíîæåñòâå V îòíîøåíèå ñìåæíîñòè. Ìàòðèöà
ñìåæíîñòè ýòîãî ãðàôà ýòî ìàòðèöà áèíàðíîãî îòíîøåíèÿ
ñìåæíîñòè. Âåðíî è îáðàòíîå âñÿêîå áèíàðíîå îòíîøåíèå ρ íà
ïðîèçâîëüíîì ìíîæåñòâå M = {m
1
,...,m
n
} ìîæíî ïðåäñòàâèòü ãðàôîì
G, âåðøèíû êîòîðîãî ñîîòâåòñòâóþò ýëåìåíòàì M, à ðåáðî (m
i
, m
j
)
â ýòîì ãðàôå ñóùåñòâóåò, åñëè è òîëüêî åñëè âûïîëíÿåòñÿ m
i
ρm
j
.
Áèíàðíàÿ ìàòðèöà îòíîøåíèÿ ρ îäíîâðåìåííî ÿâëÿåòñÿ ìàòðèöåé
ñìåæíîñòè ãðàôà G, à ñàì ãðàô íàçûâàþò ãðàôîì îòíîøåíèÿ ρ.
Ïî ìàòðèöå ñìåæíîñòè ãðàôà ìîæíî îïðåäåëèòü ñâîéñòâà îòíî-
øåíèÿ ρ. Ãðàô ðåôëåêñèâíîãî îòíîøåíèÿ ñîäåðæèò ïåòëè âî âñåõ
âåðøèíàõ è, ñîîòâåòñòâåííî, åäèíèöû âî âñåõ ýëåìåíòàõ ãëàâíîé
äèàãîíàëè ìàòðèöû ñìåæíîñòè. Ñèììåòðè÷íîìó îòíîøåíèþ
ñîîòâåòñòâóåò ãðàô ñ ñèììåòðè÷åñêîé ìàòðèöåé ñìåæíîñòè. Êàê
áûëî îòìå÷åíî âûøå, òàêîé îðãðàô ðàâíîñèëåí ïðîñòîìó íåîðèåí-
òèðîâàííîìó ãðàôó. Ãðàô òðàíçèòèâíîãî îòíîøåíèÿ îáëàäàåò
ñëåäóþùèì ñâîéñòâîì: åñëè ñóùåñòâóþò ðåáðà (v
i
, v
j
) è (v
j
, v
k
), òî

116 117Ãëàâà 8 Ãðàôû
ñóùåñòâóåò ðåáðî (v
i
, v
k
). Ãðàô îòíîøåíèÿ ýêâèâàëåíòíîñòè
ïðåäñòàâëÿåò ñîáîé ñîâîêóïíîñòü ïîëíûõ ïîäãðàôîâ.
Ïîñêîëüêó ëþáîé ãðàô ïðåäñòàâëÿåò íåêîòîðîå îòíîøåíèå, ìîæ-
íî îïðåäåëèòü îïåðàöèè îáúåäèíåíèÿ è ïåðåñå÷åíèÿ íàä ãðàôàìè
òàê æå, êàê íàä îòíîøåíèÿìè. Äîïîëíåíèþ ρ′ îòíîøåíèÿ ρ
(ò.å.îòíîøåíèþ, êîòîðîå èñòèííî, êîãäà ρ ëîæíî) ñîîòâåòñòâóåò
äîïîëíåíèå ãðàôà G äî ïîëíîãî ãðàôà, ò.å.ãðàô G′, â êîòîðîì
èìåþòñÿ òå è òîëüêî òå äóãè, êîòîðûõ íåò â G.Îáðàòíîìó îòíîøå-
íèþ ρ
1
ñîîòâåòñòâóåò ãðàô G
1
, êîòîðûé ïîëó÷åí èç ãðàôà G èçìåíå-
íèåì îðèåíòàöèè âñåõ åãî äóã íà ïðîòèâîïîëîæíûå.
8.5. Ïóòè è ñâÿçíîñòü â íåîðèåíòèðîâàííûõ ãðàôàõ
8.5.1. Îñíîâíûå îïðåäåëåíèÿ
Îïðåäåëåíèå 8.9. Ïóòü P
i
â íåîðèåíòèðîâàííîì ãðàôå ýòî
ïîñëåäîâàòåëüíîñòü ðåáåð (v
i0
,v
i1
), (v
i1
,v
i2
),..., (v
i, n1
, v
in
), òàêàÿ,
÷òî ëþáûå äâà ñîñåäíèå ðåáðà ðàçëè÷íû è èìåþò îáùóþ
èíöèäåíòíóþ èì âåðøèíó. Âåðøèíà v
i0
íàçûâàåòñÿ íà÷àëîì ïóòè,
âåðøèíà v
in
êîíöîì ïóòè.
Ïóòü ìîæíî çàäàòü òàêæå ïîñëåäîâàòåëüíîñòüþ âåðøèí, íå
óêàçûâàÿ ðåáåð, íàïðèìåð: v
i0
,v
i1
,v
i2
,..., v
i, n1
, v
in
. Â ìóëüòèãðàôå ïðè
çàäàíèè ïóòè íóæíî óêàçûâàòü èìåíà ðåáåð. ×èñëî ðåáåð â ïóòè P
íàçûâàåòñÿ åãî äëèíîé è îáîçíà÷àåòñÿ l (P).
Î÷åâèäíî, ÷òî, åñëè â íåîðèåíòèðîâàííîì ãðàôå ñóùåñòâóåò ïóòü
èç v
i0
â v
in
, òî ñóùåñòâóåò ïóòü èç v
in
â v
i0
, ýòî òîò æå ïóòü,
ïðîéäåííûé â îáðàòíîì íàïðàâëåíèè.
Ïóòü íàçûâàåòñÿ öèêëè÷åñêèì, èëè ïðîñòî öèêëîì, åñëè v
i0
= v
in
.
Öèêë íàçûâàåòñÿ ïðîñòûì, åñëè ëþáàÿ âåðøèíà ãðàôà âñòðå÷àåòñÿ
â íåì íå áîëåå îäíîãî ðàçà. Öèêë íàçûâàåòñÿ ïîëíûì, åñëè â íåãî
âõîäÿò âñå âåðøèíû ãðàôà.
Îäíî è òî æå ðåáðî ìîæåò âñòðå÷àòüñÿ â ïóòè íåñêîëüêî ðàç.
Ïóòü íàçûâàåòñÿ öåïüþ, åñëè êàæäîå ðåáðî âñòðå÷àåòñÿ â íåì íå
áîëåå îäíîãî ðàçà, è ïðîñòîé öåïüþ (èëè ïðîñòûì ïóòåì), åñëè
ëþáàÿ âåðøèíà ãðàôà âñòðå÷àåòñÿ â íåì íå áîëåå, ÷åì îäèí ðàç.
Ïðîñòàÿ öåïü ýòî öåïü, êîòîðàÿ íå ïåðåñåêàåò ñàìà ñåáÿ.
Åñëè êîíåö ïóòè P
1
ñîâïàäàåò ñ íà÷àëîì ïóòè P
2
, òî, ïðèïèñàâ
ñïðàâà ê ïîñëåäîâàòåëüíîñòè ðåáåð P
1
ïîñëåäîâàòåëüíîñòü ðåáåð P
2
,
ïîëó÷èì íîâûé ïóòü, âåäóùèé èç íà÷àëà P
1
â êîíåö P
2
. Ýòîò ïóòü
áóäåì îáîçíà÷àòü P
1
P
2
.
Ïðèìåð.
 êà÷åñòâå ïðèìåðà ðàññìîòðèì ïóòè è öèêëû â ãðàôå íà
ðèñ.8.6. Ïóòü (v
1
, v
2
), (v
2
, v
5
), (v
5
, v
7
), (v
7
,v
6
), (v
6
, v
8
) îáðàçóåò
ïðîñòóþ öåïü. Ýòó öåïü ìîæíî
çàäàòü ïîñëåäîâàòåëüíîñòüþ
âåðøèí: v
1
, v
2
, v
5
, v
7
, v
6
, v
8
. Íè
îäíà âåðøèíà â íåé íå ïîâòî-
ðÿåòñÿ. Ïóòü v
1
, v
2
, v
5
, v
7
, v
6
, v
8
,
v
7
íå ÿâëÿåòñÿ ïðîñòîé öåïüþ
îí ñîäåðæèò öèêë v
7
, v
6
, v
8
, v
7
.
Ïóòü v
1
, v
2
, v
5
, v
4
, v
3
, v
2
, v
5
, v
7
íå
ÿâëÿåòñÿ öåïüþ, òàê êàê ðåáðî
(v
2
, v
5
) ñîäåðæèòñÿ â íåì äâà
ðàçà. Ýòîò ïóòü ñîäåðæèò òàêæå
öèêë v
2
, v
5
, v
4
, v
3
, v
2
. Íàêîíåö,
ïîñëåäîâàòåëüíîñòü (v
1
,v
2
), (v
2
,v
1
) íå ñ÷èòàåòñÿ öèêëîì, ïîñêîëüêó
(v
1
, v
2
) = (v
2
, v
1
), òàê êàê ðåáðà íå îðèåíòèðîâàíû.
Îïðåäåëåíèå 8.10. Âåðøèíû v
i
è v
j
íàçûâàþòñÿ ñâÿçàííûìè,
åñëè ñóùåñòâóåò ïóòü ñ íà÷àëîì â v
i
è êîíöîì â v
j
.  ýòîì ñëó÷àå
ãîâîðÿò òàêæå, ÷òî âåðøèíà v
j
äîñòèæèìà èç âåðøèíû v
i
. Êàæäàÿ
âåðøèíà ïî îïðåäåëåíèþ ñâÿçàíà ñàìà ñ ñîáîé ïóòåì íóëåâîé
äëèíû.
Ñâÿçàííîñòü ýòî áèíàðíîå îòíîøåíèå íà ìíîæåñòâå âåðøèí.
Îíî ðåôëåêñèâíî (êàæäàÿ âåðøèíà ñâÿçàíà ñàìà ñ ñîáîé ïî
îïðåäåëåíèþ), ñèììåòðè÷íî (äëÿ êàæäîãî ïóòè èìååòñÿ îáðàòíûé
ïóòü) è òðàíçèòèâíî. Òðàíçèòèâíîñòü îçíà÷àåò, ÷òî åñëè åñòü ïóòü
èç v
i
â v
j
è ïóòü èç v
j
â v
k
, òî åñòü ïóòü èç v
i
â v
k
. Ýòî î÷åâèäíî: ÷òîáû
ïîëó÷èòü òàêîé ïóòü, äîñòàòî÷íî ê ïîñëåäîâàòåëüíîñòè ðåáåð, âåäó-
ùåé èç v
i
â v
j
, ïðèïèñàòü ñïðàâà ïîñëåäîâàòåëüíîñòü ðåáåð, âåäóùóþ
èç v
j
â v
k
.
Òàêèì îáðàçîì, îòíîøåíèå ñâÿçàííîñòè ÿâëÿåòñÿ îòíîøåíèåì
ýêâèâàëåíòíîñòè íà ìíîæåñòâå âåðøèí ãðàôà G è ðàçáèâàåò ýòî
ìíîæåñòâî íà íåïåðåñåêàþùèåñÿ ïîäìíîæåñòâà êëàññû
ýêâèâàëåíòíîñòè. Âñå âåðøèíû îäíîãî êëàññà ñâÿçàíû ìåæäó ñîáîé,
âåðøèíû èç ðàçíûõ êëàññîâ ìåæäó ñîáîé íå ñâÿçàíû. Ïîäãðàô,
îáðàçîâàííûé âñåìè âåðøèíàìè îäíîãî êëàññà, íàçûâàåòñÿ
êîìïîíåíòîé ñâÿçíîñòè ãðàôà G.Ìîæíî äàòü è äðóãîå îïðåäåëåíèå
êîìïîíåíòû ñâÿçíîñòè.
Îïðåäåëåíèå 8.11. Íåîðèåíòèðîâàííûé ãðàô íàçûâàåòñÿ
ñâÿçíûì, åñëè âñå åãî âåðøèíû ñâÿçàíû ìåæäó ñîáîé.
Ìàêñèìàëüíûé ñâÿçíûé ïîäãðàô ãðàôà G íàçûâàåòñÿ
êîìïîíåíòîé ñâÿçíîñòè ãðàôàG.
Ñâÿçíûé ãðàô ñîñòîèò èç îäíîé êîìïîíåíòû ñâÿçíîñòè.
Ðèñ. 8.6. Ïóòè è öèêëû
âíåîðèåíòèðîâàííîì ãðàôå.

118 119Ãëàâà 8 Ãðàôû
Ïðèìåð.
Ðèñ. 8.7. Ãðàôû G
1
è
G
2
ñâÿçíûå, G
3
è
G
4
íåñâÿçíûå.
Òåîðåìà 8.1. Åñëè äâå âåðøèíû ñâÿçàíû ìåæäó ñîáîé, òî
ñóùåñòâóåò ñâÿçûâàþùàÿ èõ ïðîñòàÿ öåïü.
Äîêàçàòåëüñòâî. Äåéñòâèòåëüíî, åñëè ïóòü, ñâÿçûâàþùèé äâå
âåðøèíû, íå ÿâëÿåòñÿ ïðîñòîé öåïüþ, òî â íåì èìååòñÿ âåðøèíà v,
èíöèäåíòíàÿ áîëåå ÷åì äâóì ðåáðàì ýòîãî ïóòè. Ïóñòü e
i
ïåðâîå
èç ýòèõ ðåáåð, e
j
ïîñëåäíåå (j > i+1). Òîãäà èç äàííîãî ïóòè
ìîæíî óäàëèòü ó÷àñòîê îò i+1-ãî ðåáðà äî j1-ãî. Ïîëó÷åííàÿ
ïîñëåäîâàòåëüíîñòü îñòàíåòñÿ ïóòåì: â íåé ðåáðà e
i
è e
j
ñòàíóò ñîñåä-
íèìè, è ïðè ýòîì îíè èìåþò îáùóþ âåðøèíó v. Åñëè ïîëó÷åííûé
ïóòü íå ÿâëÿåòñÿ ïðîñòîé öåïüþ, òî ïðîöåññ ïîâòîðÿåòñÿ äî ïîëó-
÷åíèÿ ïðîñòîé öåïè.
Îïðåäåëåíèå 8.12. Âåðøèíà ãðàôà íàçûâàåòñÿ òî÷êîé ñî÷ëå-
íåíèÿ, åñëè åå óäàëåíèå óâåëè÷èâàåò ÷èñëî ñâÿçíûõ êîìïîíåíò
ãðàôà. Ãðàô íàçûâàåòñÿ ðàçäåëèìûì, åñëè îí ñîäåðæèò õîòÿ áû
îäíó òî÷êó ñî÷ëåíåíèÿ, è íåðàçäåëèìûì, åñëè îí íå ñîäåðæèò
òàêèõ òî÷åê. Ìàêñèìàëüíûå íåðàçäåëèìûå ïîäãðàôû ãðàôà
íàçûâàþòñÿ åãî áëîêàìè.
Íàïðèìåð, â ãðàôå G íà ðèñ. 8.6âåðøèíû v
5
, v
2
, v
7
òî÷êè
ñî÷ëåíåíèÿ.
Òåîðåìà 8.2. Âåðøèíà v
i
ÿâëÿåòñÿ òî÷êîé ñî÷ëåíåíèÿ ñâÿçíîãî
ãðàôà G, åñëè è òîëüêî åñëè ñóùåñòâóþò òàêèå âåðøèíû v
j
è v
k
,
îòëè÷íûå îò v
i
, ÷òî ëþáîé ïóòü ìåæäó íèìè ïðîõîäèò ÷åðåç v
i
.
Äîêàçàòåëüñòâî. Ïóñòü v
i
òî÷êà ñî÷ëåíåíèÿ. Åå óäàëåíèå äàåò
íîâûé ãðàô G′, ñîäåðæàùèé íåñêîëüêî ñâÿçíûõ êîìïîíåíò.
Âûáåðåì âåðøèíû v
j
è v
k
òàê, ÷òîáû îíè ëåæàëè â ðàçíûõ êîìïî-
íåíòàõ. Òîãäà â G′ ìåæäó íèìè ïóòè íåò. Íî â G (â ñèëó åãî ñâÿç-
íîñòè) ìåæäó íèìè åñòü ïóòè (ïî êðàéíåé ìåðå îäèí). Çíà÷èò,
èìåííî óäàëåíèå v
i
ðàçîðâàëî ýòè ïóòè, è, ñëåäîâàòåëüíî, âñå îíè
ïðîõîäÿò ÷åðåç v
i
.
Ïóñòü òåïåðü ñóùåñòâóþò âåðøèíû v
j
è v
k
, óêàçàííûå â óñëîâèè
òåîðåìû. Òîãäà óäàëåíèå v
i
ðàçðûâàåò âñå ïóòè ìåæäó íèìè, ãðàô
ñòàíîâèòñÿ íåñâÿçíûì, è, ñëåäîâàòåëüíî, v
i
òî÷êà ñî÷ëåíåíèÿ.
Ðàçäåëèìûå ãðàôû íàçûâàþò åùå 1-ñâÿçíûìè. Âîîáùå,
k-ñâÿçíûì íàçûâàþò ãðàô, äëÿ íàðóøåíèÿ ñâÿçíîñòè êîòîðîãî íàäî
óäàëèòü íå ìåíåå k âåðøèí. Ìîæíî ñêàçàòü, ÷òî ÷èñëî ñâÿçíîñòè k
õàðàêòåðèçóåò íàäåæíîñòü ñâÿçíîñòè. Åñëè ãðàô èçîáðàæàåò,
íàïðèìåð, ñåòü êîììóíèêàöèé, òî ýòî ÷èñëî ãîâîðèò î òîì, ÷òî ïðè
ïîâðåæäåíèè ëþáûõ k 1óçëîâ ñåòü âñå åùå îáåñïå÷èâàåò ñâÿçü
ìåæäó ëþáûìè îñòàâøèìèñÿ óçëàìè.
8.5.2. Ðàññòîÿíèÿ. Äèàìåòð, ðàäèóñ, öåíòð
Îïðåäåëåíèå 8.13. Â íåîðèåíòèðîâàííîì ãðàôå ðàññòîÿíèåì
d(v
i
, v
j
) ìåæäó âåðøèíàìè v
i
è v
j
íàçûâàåòñÿ ìèíèìàëüíàÿ èç
äëèí ïðîñòûõ öåïåé, ñâÿçûâàþùèõ ýòè âåðøèíû.
Ïîñêîëüêó ïî îïðåäåëåíèþ êàæäàÿ âåðøèíà ñâÿçàíà ñàìà ñ
ñîáîé, òî d (v
i
, v
i
) = 0.
Ðàññòîÿíèå d (v
i
, v
j
) óäîâëåòâîðÿåò àêñèîìàì ìåòðèêè:
1. d (v
i
, v
j
) ≥ 0, ïðè÷åì d (v
i
, v
j
) = 0, åñëè è òîëüêî åñëè v
i
= v
j
;
2. d (v
i
, v
j
) = d (v
j
, v
i
);
3. d (v
i
, v
j
) + d (v
j
, v
k
) ≥ d (v
i
, v
k
) (íåðàâåíñòâî òðåóãîëüíèêà).
Âûïîëíåíèå ïåðâûõ äâóõ ñâîéñòâ î÷åâèäíî. Äîêàçàòåëüñòâî
òðåòüåãî òàêæå íåñëîæíî. Ïóñòü P
ij
êðàò÷àéøàÿ öåïü èç v
i
â v
j
,
P
jk
êðàò÷àéøàÿ öåïü èç v
j
â v
k
. Òîãäà ïóòü P
ij
P
jk
, äëèíà êîòîðîãî
ðàâíà l (P
ij
P
jk
) = l (P
ij
) + l (P
jk
) = d (v
i
, v
j
) + d (v
j
, v
k
), âåäåò èç v
i
â v
k
.
Ñëåäîâàòåëüíî, d (v
i
, v
k
) ëèáî ðàâíî d (v
i
, v
j
) + d (v
j
, v
k
), ëèáî ìåíüøå
ýòîé ñóììû, åñëè ñóùåñòâóåò áîëåå êîðîòêèé ïóòü èç v
i
â v
k
. Ñëåäî-
âàòåëüíî, àêñèîìà 3âûïîëíÿåòñÿ.
Îïðåäåëåíèå 8.14. Äèàìåòðîì d(G) ãðàôà G íàçûâàåòñÿ
ìàêñèìàëüíîå èç ðàññòîÿíèé ìåæäó åãî âåðøèíàìè:
d(G)=
,
max
ij
vv G
∈
d(v
i
, v
j
). Ìàêñèìàëüíûì óäàëåíèåì îò âåðøèíû
v
i
íàçûâàåòñÿ âåëè÷èíà r(v
i
)=
max
j
vG
∈
d(v
i
,v
j
). Âåðøèíà v
íàçûâàåòñÿ öåíòðîì ãðàôà G, åñëè r (v) ìèíèìàëüíî ñðåäè
äðóãèõ âåðøèí ãðàôà: r(v)=
min
j
vG
∈
r(v
i
). Ìàêñèìàëüíîå óäàëåíèå
r (v) îò öåíòðà v íàçûâàåòñÿ ðàäèóñîì ãðàôà G è îáîçíà÷àåòñÿ r (G).
×èñëî öåíòðîâ è ñîîòíîøåíèÿ ìåæäó ðàäèóñîì è äèàìåòðîì â
ãðàôå ìîãóò áûòü ðàçëè÷íûìè.  ïîëíîì íåîðèåíòèðîâàííîì ãðàôå
äèàìåòð è ðàäèóñ ðàâíû åäèíèöå, è âñå âåðøèíû öåíòðû. Åñëè ãðàô
G ïðîñòàÿ öåïü ñ íå÷åòíûì ÷èñëîì 2n+1âåðøèí, òî n+1-ÿ îò
íà÷àëà âåðøèíà åäèíñòâåííûé öåíòð, d (G) = 2n, r (G) = n. Åñëè æå
ãðàô G ïðîñòàÿ öåïü ñ ÷åòíûì ÷èñëîì 2n âåðøèí, òî n-ÿ è n+1-ÿ
îò íà÷àëà âåðøèíû äâà öåíòðà, d (G) = 2n1, r (G)=n1.
