Таран Т.А. Основы дискретной математики
Подождите немного. Документ загружается.


200 201
x,y∈R, çàäàåò îòíîøåíèå «áîëüøå» íà ìíîæåñòâå äåéñòâèòåëüíûõ
÷èñåë; ïîäñòàâèâ â íåãî çíà÷åíèÿ, ïîëó÷èì âûñêàçûâàíèÿ, íàïðè-
ìåð: 5>2=T, 6,8>10=F. Åñëè â ïðåäèêàò P(x,y): x>y ïîäñòà-
âèòü çíà÷åíèå y=0, ïîëó÷èì îäíîìåñòíûé ïðåäèêàò: x>0, êîòîðûé
çàäàåò ñâîéñòâî äåéñòâèòåëüíûõ ÷èñåë áûòü (èëè íå áûòü) áîëüøå
íóëÿ è îïðåäåëÿåò ïîíÿòèå «ïîëîæèòåëüíûå äåéñòâèòåëüíûå ÷èñëà».
Íà ìåñòî ïåðåìåííîé â ïðåäèêàò ìîæíî ïîäñòàâèòü ôóíêöèþ, îïðå-
äåëåííóþ íà ïðåäìåòíîé îáëàñòè ïðåäèêàòà è ïðèíèìàþùóþ çíà÷å-
íèÿ â ýòîé îáëàñòè. Íàïðèìåð, åñëè â ïðåäèêàò P(x,y) ïîäñòàâèòü
íà ìåñòî x ôóíêöèþ f(u,v)=u+v, ïîëó÷èì íîâûé ïðåäèêàò:
R(f(u,v),y): u+v>y, îïðåäåëÿþùèé îòíîøåíèå ìåæäó ñóììîé
äâóõ ÷èñåë è òðåòüèì ÷èñëîì.
Äðóãîé ïðèìåð äâóìåñòíîãî ïðåäèêàòà: S(x,y): «x ðîäèëñÿ â y
ãîäó», ãäå x∈{ëþäè}, y∈N. Ïðåäèêàò S(x,y) çàäàåò îòíîøåíèå íà
ìíîæåñòâå ëþäåé è ìíîæåñòâå öåëûõ ÷èñåë. Ïðè çàìåíå y íà îáúåêò
èç îáëàñòè îïðåäåëåíèÿ, íàïðèìåð, y=1814, ïîëó÷èì îäíîìåñòíûé
ïðåäèêàò S(x,1814), îïðåäåëÿþùèé ñâîéñòâî: «÷åëîâåê x ðîäèëñÿ â
1814 ãîäó». Ïðè çàìåíå îáåèõ ïåðåìåííûõ ïîëó÷èì âûñêàçûâàíèå,
íàïðèìåð, «Ëåðìîíòîâ ðîäèëñÿ â 1814 ãîäó».
Òàêèì îáðàçîì, äâóìåñòíûé ïðåäèêàò çàäàåò íåêîòîðîå áèíàðíîå
îòíîøåíèå íà çàäàííûõ ìíîæåñòâàõ, ïðè÷åì ïðè çàìåíå îäíîé
ïåðåìåííîé ìåñòíîñòü ïðåäèêàòà ïîíèæàåòñÿ (äâóìåñòíûé ïðåäèêàò
ñòàíîâèòñÿ îäíîìåñòíûì), à ïðè çàìåíå îáåèõ ïåðåìåííûõ íà
ïðåäìåòíûå ïîñòîÿííûå îí îáðàùàåòñÿ â âûñêàçûâàíèå.
 îáùåì ñëó÷àå n-ìåñòíûé ïðåäèêàò îïðåäåëÿåò n-ìåñòíîå îòíîøåíèå.
Îïðåäåëåíèå 12.2. N-ìåñòíûì ïðåäèêàòîì, îïðåäåëåííûì íà
ìíîæåñòâàõ Ì1, Ì2,, Ìn, íàçûâàåòñÿ âûðàæåíèå, êîòîðîå
îáðàùàåòñÿ â âûñêàçûâàíèå ïðè çàìåíå êàæäîé ïðåäìåòíîé ïåðå-
ìåííîé íà ýëåìåíò èç åå îáëàñòè îïðåäåëåíèÿ. Åñëè âñå ïðåäìåò-
íûå ïåðåìåííûå îïðåäåëåíû íà îäíîì è òîì æå ìíîæåñòâå, òî
ïðåäèêàò íàçûâàåòñÿ îäíîðîäíûì.
Ïðèìåðû.
R(x,y, z, t): «x ðîäèëñÿ â y ãîäó â ãîðîäå z, èìååò îáðàçîâàíèå t»,
x∈{ëþäè}, y∈N, z∈ {ãîðîäà}, t ∈ {íà÷àëüíîå, ñðåäíåå, âûñøåå}.
R(x,y, z, t) íåîäíîðîäíûé ÷åòûðåõìåñòíûé ïðåäèêàò. Îäíîðîäíûé
ïðåäèêàò: Q(x,y, z): «ïàðàëëåëåïèïåä èìååò âûñîòó x, øèðèíó y,
äëèíó z», ãäå x,y, z∈R.
Òåîðèÿ ïðåäèêàòîâ ïåðâîãî ïîðÿäêàÃëàâà 12
12.2. Ôîðìóëû ëîãèêè ïðåäèêàòîâ
12.2.1. Îïåðàöèè íàä ïðåäèêàòàìè
Ïðåäèêàò ìîæíî ðàññìàòðèâàòü êàê ôóíêöèþ, îïðåäåëåííóþ
íà íåêîòîðîì ìíîæåñòâå îáúåêòîâ è ïðèíèìàþùóþ äâà çíà÷åíèÿ,
T è F. Ïîýòîìó íàä ïðåäèêàòàìè îïðåäåëåíû âñå áóëåâû îïåðàöèè:
¬ (îòðèöàíèå), & (êîíúþíêöèÿ), ∨ (äèçúþíêöèÿ), → (èìïëèêàöèÿ),
≡ (ýêâèâàëåíòíîñòü), à òàêæå äâå íîâûå îïåðàöèè îïåðàöèè
íàâåøèâàíèÿ êâàíòîðîâ: ∀ âñåîáùíîñòè è ∃ ñóùåñòâîâàíèÿ.
Åñëè P(x) îïðåäåëÿåò íåêîòîðîå ñâîéñòâî íà ìíîæåñòâå Ì, òî
ôîðìóëà ∀xP(x) îáîçíà÷àåò âûñêàçûâàíèå: «äëÿ âñÿêîãî ïðåäìåòà
x ∈ Ì ñâîéñòâî P(x) âûïîëíåíî», èëè «âñå x îáëàäàþò ñâîéñòâîì
P(x)». Çíà÷åíèå ôîðìóëû |∀xP(x)| = T (èñòèííî), åñëè ñâîéñòâî P
âûïîëíåíî äëÿ âñåõ îáúåêòîâ èç Ì, è |∀xP(x)| = F (ëîæíî), åñëè
ñóùåñòâóåò õîòÿ áû îäèí ýëåìåíò x=a, a∈Ì, äëÿ êîòîðîãî
ñâîéñòâî P íå âûïîëíåíî, ò.å. |P(a)| = F. Íàïðèìåð: åñëè P(x): x
ñìåðòåí, x∈{ëþäè}, òî ∀xP(x) «âñå ëþäè ñìåðòíû» (çíà÷åíèå
ôîðìóëû |∀xP(x)|=T); åñëè P(x):x>0,x∈R, òî ∀xP(x) «âñå
äåéñòâèòåëüíûå ÷èñëà ïîëîæèòåëüíû» (|∀xP(x)|=F).
Ôîðìóëà ∃xP(x) îçíà÷àåò: «ñóùåñòâóåò ïî êðàéíåé ìåðå îäèí
ïðåäìåò x, îáëàäàþùèé ñâîéñòâîì P(x)», èëè: «íåêîòîðûå x îáëà-
äàþò ñâîéñòâîì P(x)». Çíà÷åíèå ôîðìóëû |∃xP(x)| = T (èñòèííî),
åñëè ñóùåñòâóåò õîòÿ áû îäèí ýëåìåíò x= a, a∈Ì, äëÿ êîòîðîãî
ñâîéñòâî P âûïîëíåíî: |P(a)| = T; çíà÷åíèå |∃xP(x)|=F (ëîæíî),
åñëè ñâîéñòâî P íå âûïîëíåíî äëÿ âñåõ îáúåêòîâ èç Ì. Íàïðèìåð:
åñëè P(x):x>0,x∈R, òî ∃xP(x) ýòî âûñêàçûâàíèå: «íåêîòîðûå
äåéñòâèòåëüíûå ÷èñëà ïîëîæèòåëüíû», òîãäà |∃xP(x)|=T; åñëè P(x):
x ñìåðòåí, x∈{ëþäè}, òî ∃x¬P(x) «ñóùåñòâóþò áåññìåðòíûå
ëþäè» (ëîæíîå âûñêàçûâàíèå).
Åñëè Ì = {a
1
, a
2
, , a
n
} êîíå÷íàÿ îáëàñòü îïðåäåëåíèÿ
ïðåäèêàòà P(x), òî ôîðìóëû ñ êâàíòîðàìè ìîãóò áûòü âûðàæåíû
÷åðåç êîíúþíêöèþ è äèçúþíêöèþ:
∀xP(x) = P(a
1
)&P(a
2
) && P(a
n
), ∃xP(x) = P(a
1
) ∨ P(a
2
) ∨∨P(a
n
).
Òàêèì îáðàçîì, êâàíòîð âñåîáùíîñòè ÿâëÿåòñÿ îáîáùåíèåì
êîíúþíêöèè, à êâàíòîð ñóùåñòâîâàíèÿ îáîáùåíèåì äèçúþíêöèè
íà áåñêîíå÷íóþ îáëàñòü îïðåäåëåíèÿ.
Êâàíòîðû ∀ è ∃ ñâÿçàíû äðóã ñ äðóãîì ïî ïðèíöèïó äâîéñòâåí-
íîñòè (ïî çàêîíàì äå Ìîðãàíà):
¬∀xP(x)≡∃x¬P(x),¬∃xP(x)≡∀x¬P(x).
Íàïðèìåð, åñëè P(x): «x ñìåðòåí», x ∈ {ëþäè}, òî ôîðìóëà ¬∀xP(x)
îáîçíà÷àåò âûñêàçûâàíèå: «íå âñå ëþäè ñìåðòíû», êîòîðîå ýêâèâà-
ëåíòíî âûñêàçûâàíèþ «ñóùåñòâóþò áåññìåðòíûå ëþäè», ò.å.

202 203Òåîðèÿ ïðåäèêàòîâ ïåðâîãî ïîðÿäêàÃëàâà 12
∃x¬P(x), à ôîðìóëà ¬∃xP(x) «íå ñóùåñòâóåò ñìåðòíûõ ëþäåé»
ýêâèâàëåíòíà âûñêàçûâàíèþ «âñå ëþäè áåññìåðòíû», ò.å. ∀x¬P(x).
12.2.2. Îïðåäåëåíèå ôîðìóëû
Îñíîâíûìè ñèìâîëàìè ÿçûêà ëîãèêè ïðåäèêàòîâ ÿâëÿþòñÿ:
• ïðîïîçèöèîíàëüíûå ñèìâîëû ¬ è →,
• êâàíòîðû âñåîáùíîñòè ∀ è ñóùåñòâîâàíèÿ ∃,
• âñïîìîãàòåëüíûå ñèìâîëû: çàïÿòàÿ , è ñêîáêè (, ),
• ïðåäìåòíûå ïåðåìåííûå x
1
, x
2
,, x
n
,,
• ïðåäìåòíûå ïîñòîÿííûå a
1
, a
2
,, a
n
,,
• ôóíêöèîíàëüíûå ñèìâîëû f
1
1
, f
1
2
,, f
k
j
,,
• ïðåäèêàòíûå ñèìâîëû P
1
1
, P
1
2
,, P
k
j
,.
Íèæíèé èíäåêñ ïðåäèêàòíîãî èëè ôóíêöèîíàëüíîãî ñèìâîëà
ýòî íîìåð, êîòîðûé ñëóæèò äëÿ ðàçëè÷åíèÿ îäíîèìåííûõ ñèìâîëîâ
ñ îäèíàêîâûì ÷èñëîì àðãóìåíòîâ, âåðõíèé èíäåêñ óêàçûâàåò ÷èñëî
àðãóìåíòîâ.
Îïðåäåëèì ïîíÿòèÿ òåðìà è ôîðìóëû.
Îïðåäåëåíèå òåðìà.
1. Êàæäàÿ ïðåäìåòíàÿ ïåðåìåííàÿ åñòü òåðì.
2. Êàæäàÿ ïðåäìåòíàÿ ïîñòîÿííàÿ åñòü òåðì.
3. Åñëè f
k
j
ôóíêöèîíàëüíûé ñèìâîë è t
1
,, t
n
òåðìû, òî f
k
j
(t
1
,,
t
n
) åñòü òåðì.
4. Äðóãèõ òåðìîâ íåò.
Îïðåäåëåíèå ôîðìóëû.
1. P
i
n
(t
1
,, t
n
), ãäå P
i
n
ïðåäèêàòíûé ñèìâîë, t
1
,, t
n
òåðìû,
åñòü àòîìàðíàÿ (ýëåìåíòàðíàÿ) ôîðìóëà.
2. Åñëè À è Â ôîðìóëû è x ïðåäìåòíàÿ ïåðåìåííàÿ, òî
ôîðìóëàìè ÿâëÿþòñÿ (¬À), (À→Â), (∀xÀ), (∃xA).
3. Äðóãèõ ôîðìóë íåò.
Âûðàæåíèÿ A&B, A ∨ B, A ≡ B îïðåäåëÿþòñÿ òàê æå, êàê â
èñ÷èñëåíèè L.
Îïðåäåëåíèå 12.3. Ôîðìóëà, íà êîòîðóþ ðàñïðîñòðàíÿåòñÿ äåé-
ñòâèå êâàíòîðà, íàçûâàåòñÿ îáëàñòüþ äåéñòâèÿ êâàíòîðà. Ïåðå-
ìåííàÿ, ïî êîòîðîé íàâåøèâàåòñÿ êâàíòîð è ïîïàäàþùàÿ â åãî
îáëàñòü äåéñòâèÿ, íàçûâàþòñÿ ñâÿçàííîé ïåðåìåííîé. Ïåðå-
ìåííàÿ, ëåæàùàÿ âíå îáëàñòè äåéñòâèÿ êâàíòîðà, íàçûâàþòñÿ
ñâîáîäíîé ïåðåìåííîé.
Ôîðìóëà, íå ñîäåðæàùàÿ ñâîáîäíûõ ïåðåìåííûõ, íàçûâàåòñÿ
çàìêíóòîé. Çàìêíóòûå ôîðìóëû ÿâëÿþòñÿ âûñêàçûâàíèÿìè.
Îáëàñòü äåéñòâèÿ êâàíòîðà îãðàíè÷èâàåòñÿ ñêîáêàìè, åñëè îíà
ñîäåðæèò áîëåå îäíîãî ïðåäèêàòà.
Ïðèìåðû.
1. Íà ðèñ. 12.2 ïðèâåäåíû ïðèìåðû ôîðìóë ëîãèêè ïðåäèêàòîâ è
óêàçàíû ñâîáîäíûå è ñâÿçàííûå ïåðåìåííûå.
Ðèñ. 12.2. Ñâîáîäíûå è ñâÿçàííûå ïåðåìåííûå.
2. Ïóñòü Q(x,y): «x ðîäèëñÿ â y ãîäó», x ∈ {ëþäè}, y ∈ {ãîäû}, òîãäà
ôîðìóëà ∀x∃yQ(x,y) îáîçíà÷àåò âûñêàçûâàíèå: «Êàæäûé ÷åëîâåê
ðîäèëñÿ â êàêîì-íèáóäü ãîäó», à ôîðìóëà ∃y∀xQ(x,y) âûñêàçû-
âàíèå: «Ñóùåñòâóåò òàêîé ãîä, â êîòîðîì ðîäèëèñü âñå ëþäè». Èç
ýòîãî ïðèìåðà âèäíî, ÷òî ðàçíîèìåííûå êâàíòîðû â îáùåì ñëó÷àå
íå ïåðåñòàíîâî÷íû.
 ôîðìóëàõ ëîãèêè ïðåäèêàòîâ ìîæíî äåëàòü çàìåíó ïåðåìåí-
íûõ (â îáùåì ñëó÷àåâ òåðìîâ) ïðè âûïîëíåíèè îïðåäåëåííûõ
óñëîâèé, êîòîðûå ñâîäÿòñÿ ê òîìó, ÷òîáû íèêàêîå ñâîáîäíîå
âõîæäåíèå ïåðåìåííîé íå ñòàëî ñâÿçàííûì â ðåçóëüòàòå çàìåíû.
Îïðåäåëåíèå 12.4. Ãîâîðÿò, ÷òî òåðì ó ñâîáîäåí äëÿ ïåðåìåííîé
õ â ôîðìóëå À(õ), åñëè íèêàêîå ñâîáîäíîå âõîæäåíèå õ â À(õ)
íå ëåæèò â îáëàñòè äåéñòâèÿ íèêàêîãî êâàíòîðà ïî z, ãäå z
ïåðåìåííàÿ, âõîäÿùàÿ â òåðì ó.
Âñÿêèé òåðì, íå ñîäåðæàùèé ïåðåìåííûõ, ñâîáîäåí äëÿ ëþáîé
ïåðåìåííîé â ëþáîé ôîðìóëå. Âñÿêèé òåðì ñâîáîäåí äëÿ õ â ôîð-
ìóëå À(õ), åñëè À(õ) íå ñîäåðæèò ñâîáîäíûõ âõîæäåíèé õ. Òåðì ó
ñâîáîäåí äëÿ ëþáîé ïåðåìåííîé â ôîðìóëå À, åñëè íèêàêàÿ ïåðå-
ìåííàÿ òåðìà ó íå ÿâëÿåòñÿ ñâÿçàííîé ïåðåìåííîé â ôîðìóëå À.
Ïðèìåðû.
∃x(x=2y), x, y ∈ R. Â ýòîé ôîðìóëå z ñâîáîäíî äëÿ y: ∃x(x=2z).
Òåðì f(x,z) ñâîáîäåí äëÿ x â ôîðìóëå ∀yA(x,y)→ B(x), íî íå
ñâîáîäåí äëÿ x â ôîðìóëå ∃z∀yA(x,y)→B(x).

204 205Òåîðèÿ ïðåäèêàòîâ ïåðâîãî ïîðÿäêàÃëàâà 12
12.3. Èíòåðïðåòàöèÿ ôîðìóë ëîãèêè ïðåäèêàòîâ
Ôîðìóëû èìåþò ñìûñë òîëüêî òîãäà, êîãäà èìååòñÿ êàêàÿ-ëèáî
èíòåðïðåòàöèÿ âõîäÿùèõ â íåå ñèìâîëîâ.
Îïðåäåëåíèå 12.5. Ïîä èíòåðïðåòàöèåé áóäåì ïîíèìàòü ñèñòå-
ìó, ñîñòîÿùóþ èç íåïóñòîãî ìíîæåñòâà D, íàçûâàåìîãî îáëàñòüþ
èíòåðïðåòàöèè, à òàêæå ñîîòâåòñòâèÿ, ñòàâÿùåãî êàæäîé ïðåäè-
êàòíîé áóêâå P
i
n
íåêîòîðîå îòíîøåíèå íà îáëàñòè D, êàæäîé
ïðåäìåòíîé ïîñòîÿííîé a
i
íåêîòîðûé ýëåìåíò èç îáëàñòè D,
êàæäîé ôóíêöèîíàëüíîé áóêâå f
i
n
íåêîòîðóþ n-ìåñòíóþ
îïåðàöèþ íà îáëàñòè D (ò.å. ôóíêöèþ D
n
→ D).
Ïðè çàäàííîé èíòåðïðåòàöèè âñå ïðåäìåòíûå ïåðåìåííûå ïðîáå-
ãàþò âñå çíà÷åíèÿ èç îáëàñòè D, à ëîãè÷åñêèå ñâÿçêè èìåþò îáû÷íûé
ëîãè÷åñêèé ñìûñë.
Äëÿ çàäàííîé èíòåðïðåòàöèè âñÿêàÿ çàìêíóòàÿ ôîðìóëà ïðåä-
ñòàâëÿåò ñîáîé âûñêàçûâàíèå, êîòîðîå èñòèííî èëè ëîæíî, à ôîðìó-
ëà ñî ñâîáîäíûìè ïåðåìåííûìè âûðàæàåò îòíîøåíèå íà îáëàñòè
D, êîòîðîå ìîæåò áûòü èñòèííî (âûïîëíåíî) ïðè îäíèõ çíà÷åíèÿõ
ïåðåìåííûõ è ëîæíî (íå âûïîëíåíî) ïðè äðóãèõ.
Ïðèìåðû.
1. Â òàáëèöå 12.1. ïðèâåäåíû òðè èíòåðïðåòàöèè îäíîé è òîé æå
ôîðìóëû.
Òàáëèöà 12.1.
2. Ïóñòü äàíà ôîðìóëà ∃x∃yP(f(x,y),t). Ïðåäèêàò P(v,u)
äâóìåñòíûé, ïåðåìåííûå õ, ó ñâÿçàííûå, t ñâîáîäíàÿ ïåðåìåííàÿ.
Çàäàäèì ñëåäóþùóþ èíòåðïðåòàöèþ: îáëàñòü èíòåðïðåòàöèè D
ìíîæåñòâî äåéñòâèòåëüíûõ ÷èñåë R, t=1, f(x,y)=x
2
+y
2
, ïðåäèêàò
P(u,t): u=t. Òîãäà ôîðìóëà èìååò âèä: ∃x∃y(x
2
+y
2
=1). Îíà
èñòèííà, òàê êàê ñóùåñòâóþò òàêèå x è y, êîòîðûå óäîâëåòâîðÿþò
óðàâíåíèþ îêðóæíîñòè x
2
+y
2
=1.
Åñëè ïîëîæèòü f(x,y)=x
2
+y
2
, t=r
2
, òî ôîðìóëà
∃x∃y(x
2
+y
2
=r
2
) îäíîìåñòíûé ïðåäèêàò, îáëàñòü èñòèííîñòè
êîòîðîãî ìíîæåñòâî äåéñòâèòåëüíûõ ÷èñåë, óäîâëåòâîðÿþùèõ
óðàâíåíèþ îêðóæíîñòè x
2
+y
2
=r
2
ñ ðàäèóñîì r.
Îïðåäåëåíèå 12.6. Èíòåðïðåòàöèÿ íàçûâàåòñÿ ìîäåëüþ äëÿ
äàííîãî ìíîæåñòâà ôîðìóë Γ, åñëè êàæäàÿ ôîðìóëà èç Γ
èñòèííà â äàííîé èíòåðïðåòàöèè.
Îïðåäåëåíèå 12.7. Ôîðìóëà íàçûâàåòñÿ âûïîëíèìîé, åñëè
ñóùåñòâóåò õîòÿ áû îäíà èíòåðïðåòàöèÿ, íà êîòîðîé ôîðìóëà
èñòèííà.
Îïðåäåëåíèå 12.8. Ôîðìóëà íàçûâàåòñÿ ëîãè÷åñêè îáùåçíà÷èìîé
(ËÎÇ), åñëè îíà èñòèííà íà ëþáîé èíòåðïðåòàöèè äëÿ ëþáûõ
çíà÷åíèé ïåðåìåííûõ.
Òàê æå, êàê òàâòîëîãèè, ëîãè÷åñêè îáùåçíà÷èìûå ôîðìóëû îáîç-
íà÷àþòñÿ: |= A(x).
Îïðåäåëåíèå 12.9. Ôîðìóëà, êîòîðàÿ ëîæíà íà ëþáîé èíòåð-
ïðåòàöèè ïðè ëþáûõ çíà÷åíèÿõ ïåðåìåííûõ, íàçûâàåòñÿ ïðîòè-
âîðå÷èåì.
Ëîãè÷åñêè îáùåçíà÷èìûå ôîðìóëû ÿâëÿþòñÿ âûäåëåííûìè
ôîðìóëàìè ëîãèêè ïðåäèêàòîâ.
Òàê êàê îáëàñòü îïðåäåëåíèÿ ïðåäèêàòà ìîæåò áûòü áåñêîíå÷íîé,
òî, î÷åâèäíî, ÷òî ïîñòðîåíèå òàáëèöû èñòèííîñòè íå ìîæåò ñëóæèòü
àëãîðèòìîì äëÿ îïðåäåëåíèÿ ëîãè÷åñêîé îáùåçíà÷èìîñòè ôîðìóë.
Îäíàêî ñóùåñòâóþò äðóãèå ñïîñîáû, êîòîðûå â ÷àñòíûõ ñëó÷àÿõ
ïîçâîëÿþò îïðåäåëèòü ëîãè÷åñêóþ îáùåçíà÷èìîñòü, âûïîëíèìîñòü
èëè ýêâèâàëåíòíîñòü ôîðìóë. Ìîæíî ñòðîèòü òàáëèöû èñòèííîñòè
ôîðìóë ëîãèêè ïðåäèêàòîâ äëÿ ÷àñòè÷íûõ èíòåðïðåòàöèé íà
îãðàíè÷åííûõ êîíå÷íûõ îáëàñòÿõ. Íàïðèìåð, âîçüìåì îáëàñòü
èíòåðïðåòàöèè, ñîñòîÿùóþ èç äâóõ ïðîèçâîëüíûõ ýëåìåíòîâ:
D={a, b}. Ïîñòðîèì òàáëèöó èñòèííîñòè ôîðìóë: E
1
=∃xP(x) è
E
2
=∀xP(x). Îäíîìåñòíûé ïðåäèêàò íà îáëàñòè îïðåäåëåíèÿ èç
äâóõ ýëåìåíòîâ ìîæåò ïðèíèìàòü îäíî èç ÷åòûðåõ çíà÷åíèé, êîòî-
ðûå îïðåäåëÿþòñÿ òàáëèöàìè èñòèííîñòè (òàáë. 12.2).
Òàáëèöà.12.2
Ôîðìóëû Å
1
è Å
2
áóäóò ïðèíèìàòü íà ýòèõ èíòåðïðåòàöèÿõ
ñëåäóþùèå çíà÷åíèÿ (òàáë. 12.3).
Îáëàñòü Èíòåðïðåòàöèÿ Âûñêàçûâàíèå
èíòåðïðåòàöèè D ∀x(P(x) → Q(x))
Ìíîæåñòâî P(x): x ðûáà, Âñå ðûáû æèâóò
æèâûõ ñóùåñòâ Q(x): x æèâåò â âîäå. â âîäå.
Ìíîæåñòâî P(x): x ÷åëîâåê, Âñå ëþäè ñìåðòíû.
æèâûõ ñóùåñòâ Q(x): x ñìåðòåí.
Ìíîæåñòâî P(x): x äåëèòñÿ íà 6, Âñå ÷èñëà, êîòîðûå
öåëûõ ÷èñåë Q(x): x äåëèòñÿ íà 3. äåëÿòñÿ íà 6,
äåëÿòñÿ íà 3.
xÐ
1
(.) Ð
2
(.) Ð
3
(.) Ð
4
(.)
aFFTT
bFTFT

206 207Òåîðèÿ ïðåäèêàòîâ ïåðâîãî ïîðÿäêàÃëàâà 12
Òàáëèöà.12.3
Ïîñòðîèì òàáëèöû èñòèííîñòè íà îáëàñòè èíòåðïðåòàöèè èç
äâóõ ýëåìåíòîâ D={a, b} äëÿ ñëåäóþùèõ ôîðìóë:
E
1
=∀yP(y)→∃xQ(x), E
2
=∀y(P(y)→∃xQ(x)), E
3
=
=∀y∃x(P(y) →Q(x)). Äëÿ ýòèõ ôîðìóë ñóùåñòâóåò 16 èíòåðïðå-
òàöèé, òàê êàê êàæäûé èç îäíîìåñòíûõ ïðåäèêàòîâ P è Q ïðèíèìàåò
ïî 4 çíà÷åíèÿ â ñîîòâåòñòâèè ñ òàáëèöåé 12.2. Ðàññìîòðèì âû÷èñ-
ëåíèå çíà÷åíèé ôîðìóë íà èíòåðïðåòàöèè P
2
, Q
1
.
E
1
=∀yP
2
(y)→∃xQ
1
(x) = F → F = T;
E
2
=∀y(P
2
(y)→∃xQ
1
(x)) =
21
21
(
1
)()
(
2
)()
Px
Q
x
y
Px
Q
x
→∃
∀
→∃
=
=
FFT
y
TFF
→=
∀
→=
= F;
E
3
=∀y∃x(P
2
(y)→Q
1
(x)) =
21
21
((
1
)()
((
2
)()
xP
Q
x
y
xP
Q
x
∃→
∀
∃→
=
=
21
21
21
21
(
1
)(
1
)
(
1
)(
2
)
(
2
)(
1
)
(
2
)(
2
)
P
Q
x
P
Q
y
P
Q
x
P
Q
→
∃
→
∀
→
∃
→
=
FFT
xT
FFT
y
TFF
xF
TFF
→=
∃=
→=
∀
→=
∃=
→=
= F.
Èñòèííîñòíûå çíà÷åíèÿ Å
1
, Å
2
, Å
3
äëÿ âîñüìè èíòåðïðåòàöèé
ïðèâåäåíû â òàáë. 12.4.
Òàáëèöà. 12.4.
P(.) ∃xP(x) ∀xP(x)
P
1
FF
P
2
TF
P
3
TF
P
4
TT
P(.) Q(.) E
1
E
2
E
3
P
1
Q
1
T T T
P
1
Q
2
T T T
P
1
Q
3
T T T
P
1
Q
4
T T T
P
2
Q
1
T F F
P
2
Q
2
T T T
P
2
Q
3
T T T
P
2
Q
4
T T T
Èç òàáëèöû âèäíî, ÷òî ôîðìóëà Å
1
íå ýêâèâàëåíòíà ôîðìóëàì
Å
2
è Å
3
, à ôîðìóëû Å
2
è Å
3
, âîçìîæíî, ýêâèâàëåíòû, äëÿ îêîí÷à-
òåëüíîãî ðåøåíèÿ íóæíî ðàññìîòðåòü îñòàâøèåñÿ èíòåðïðåòàöèè.
12.4. Ëîãè÷åñêè îáùåçíà÷èìûå ôîðìóëû
ëîãèêè ïðåäèêàòîâ
12.4.1. Îñíîâíûå ëîãè÷åñêè îáùåçíà÷èìûå ôîðìóëû
ëîãèêè ïðåäèêàòîâ
Îñíîâíûå ëîãè÷åñêè îáùåçíà÷èìûå ôîðìóëû ëîãèêè ïðåäè-
êàòîâ ïðèâåäåíû â òàáëèöå 12.5.
Êàæäàÿ ëîãè÷åñêè îáùåçíà÷èìàÿ ôîðìóëà âûðàæàåò íåêîòîðîå
èñòèííîå âûñêàçûâàíèå îòíîñèòåëüíî ñâîéñòâ îáúåêòîâ. Íàïðèìåð,
ëîãè÷åñêè îáùåçíà÷èìàÿ ôîðìóëà ∃x(P(x)&Q(x))→∃xP(x)&∃xQ(x)
âûðàæàåò òîò ôàêò, ÷òî åñëè íåêîòîðûå îáúåêòû îáëàäàþò ñðàçó
äâóìÿ ñâîéñòâàìè P è Q, òî ñóùåñòâóþò îáúåêòû, îáëàäàþùèå ñâîé-
ñòâîì P, è îáúåêòû, îáëàäàþùèå ñâîéñòâîì Q. Òàê, åñëè ñóùåñòâóþò
þðèñòû-æóëèêè, òî ñóùåñòâóþò ëþäè, êîòîðûå ÿâëÿþòñÿ þðèñòàìè,
è ñóùåñòâóþò æóëèêè. Î÷åâèäíî, ÷òî îáðàòíàÿ èìïëèêàöèÿ
∃xP(x)&∃xQ(x)→∃x(P(x)&Q(x))áóäåò èñòèííà äàëåêî íå âñåã-
äà: èç òîãî, ÷òî ñóùåñòâóþò þðèñòû è ñóùåñòâóþò æóëèêè, åùå íå
ñëåäóåò, ÷òî ñóùåñòâóþò þðèñòû-æóëèêè, ýòè äâà ìíîæåñòâà ìîãóò
íå ïåðåñåêàòüñÿ.
Íèæå ïðèâîäÿòñÿ èíòåðïðåòàöèè íåêîòîðûõ ëîãè÷åñêè îáùåçíà-
÷èìûõ ôîðìóë.
∀xP(x)→P(y) Åñëè âñå ëþäè ñìåðòíû, òî
ñìåðòåí ëþáîé ÷åëîâåê.
P(a)→∃x(P(x)) Åñëè êîøêà a ñåðàÿ, òî
ñóùåñòâóþò ñåðûå êîøêè.
¬∀xP(x)≡∃x¬P(x) Íå âñå êîøêè ñåðûå ≡
Ñóùåñòâóþò íå ñåðûå êîøêè.
¬∃xP(x)≡∀x¬P(x) Íå ñóùåñòâóåò ñåðûõ êîøåê ≡
Âñå êîøêè íå ñåðûå.
∀x(P(x) & Q(x)) ≡ Âñå êîøêè ñ óñàìè è ñ õâîñòàìè ≡
≡∀xP(x) & ∀xQ(x) Êàæäàÿ êîøêà èìååò óñû
è êàæäàÿ êîøêà èìååò õâîñò.
∃x(P(x)∨Q(x)) ≡ Íåêîòîðûå êîøêè áåëûå èëè
≡∃xP(x)∨∃xQ(x) ÷åðíûå ≡ Ñóùåñòâóåò õîòÿ áû
îäíà áåëàÿ êîøêà èëè ñóùåñòâóåò
õîòÿ áû îäíà ÷åðíàÿ êîøêà.

208 209Òåîðèÿ ïðåäèêàòîâ ïåðâîãî ïîðÿäêàÃëàâà 12
Òàáëèöà 12.5.
¹ Îáùåçíà÷èìûå ôîðìóëû
ï/ï è êîììåíòàðèé
12
1 ∀xP(x)→P(y)
ïðàâèëî óíèâåðñàëüíîé êîíêðåòèçàöèè;
2 P(a)→∃x(P(x))
ïðàâèëî ýêçèñòåíöèàëüíîãî îáîáùåíèÿ;
3 ¬∀xP(x)≡∃x¬P(x)
ïðàâèëî äå Ìîðãàíà
4 ¬∃xP(x)≡∀x¬P(x)
ïðàâèëî äå Ìîðãàíà
5 ∀x(P(x)&Q(x))≡∀xP(x)&∀xQ(x)
çàêîí ïðîíåñåíèÿ ∀ ÷åðåç &
6 ∃x(P(x)∨Q(x))≡∃xP(x)∨∃xQ(x)
çàêîí ïðîíåñåíèÿ ∃ ÷åðåç ∨
7 ∀xP(x)∨∀xQ(x)→∀x(P(x)∨Q(x))
çàêîí ïðîíåñåíèÿ ∀ ÷åðåç ∨
8 ∃x(P(x) & Q(x))→∃xP(x) & ∃xQ(x)
çàêîí ïðîíåñåíèÿ ∃ ÷åðåç &
9(∀x(P(x)→Q(x))→(∀xP(x)→∀xQ(x))
çàêîí ïðîíåñåíèÿ ∀ ÷åðåç →
10 (∃xP(x)→∃xQ(x))→∃x(P(x)→Q(x))
çàêîí ïðîíåñåíèÿ ∃ ÷åðåç →
11 ∀x(P(x)≡Q(x))→(∀xP(x)≡∀xQ(x))
çàêîí ïðîíåñåíèÿ ∀ ÷åðåç ≡
12 ∀x(P(x) & B)≡∀xP(x) & B
B íå ñîäåðæèò âõîæäåíèé õ
Ïðîäîëæåíèå òàáë. 12.5.
12
13 ∀x(P(x)∨B)≡∀xP(x)∨B
B íå ñîäåðæèò âõîæäåíèé õ
14 ∃x(P(x) & B)≡∃xP(x) & B
B íå ñîäåðæèò âõîæäåíèé õ
15 ∃x(P(x)∨B)≡∃xP(x)∨B
B íå ñîäåðæèò âõîæäåíèé õ
16 ∀x(P(x)→B)≡(∃xP(x)→B)
B íå ñîäåðæèò âõîæäåíèé õ
17 ∃x(P(x)→B)≡(∀xP(x)→B)
B íå ñîäåðæèò âõîæäåíèé õ
18 ∀x∀yP(x,y)≡∀y∀xP(x,y)
çàêîí ïåðåñòàíîâêè êâàíòîðîâ ∀
19 ∀x∀yP(x,y)→∀xP(x,x)
20 ∃x∃yP(x,y)≡∃y∃xP(x,y)
çàêîí ïåðåñòàíîâêè êâàíòîðîâ ∃
21 ∃xP(x,x)→∃x∃yP(x,y)
22 ∃y∀xP(x,y)→∀x∃yP(x,y)
çàêîí ïåðåñòàíîâêè êâàíòîðîâ ∃ è ∀
23 ∀xP(x)→∃xP(x)
24 (∀xP(x)→∃xQ(x)) ≡ ∃x(P(x)→Q(x))
25 (∃xP(x)→∀xQ(x)) → ∀x(P(x)→Q(x))
26 ∀xP(x)≡∀yP(y)
åñëè ó ñâîáîäíî äëÿ x â P(x)
27 ∃xP(x)≡∃yP(y)
åñëè ó ñâîáîäíî äëÿ x â P(x)

210 211
∀x(P(x)→Q(x)) → Åñëè âñå ñòîðîæåâûå ñîáàêè çëû,
→(∀xP(x)→∀xQ(x)) òî åñëè âñå ñîáàêè ñòîðîæåâûå,
òî âñå îíè çëû. Îáðàòíîå
íå âñåãäà âåðíî.
(∃xP(x)→∃xQ(x))→ Åñëè èç òîãî, ÷òî ñóùåñòâóþò
→∃x(P(x)→Q(x)) ñîáàêè, ñëåäóåò, ÷òî ñóùåñòâóþò
ëàþùèå ñóùåñòâà, òî ñóùåñòâóþò
òàêèå ñîáàêè, êîòîðûå ëàþò.
Îáðàòíîå íå âñåãäà âåðíî.
12.4.2. Ïðîâåðêà îáùåçíà÷èìîñòè ôîðìóë ëîãèêè
ïðåäèêàòîâ
Ïðîâåðêà ëîãè÷åñêîé îáùåçíà÷èìîñòè ôîðìóë ìîæåò áûòü îñó-
ùåñòâëåíà ñâåäåíèåì ê ïðîòèâîðå÷èþ, ò.å. ìåòîäîì ðåäóêöèè. Ïðåä-
ïîëàãàåì, ÷òî ñóùåñòâóåò òàêàÿ èíòåðïðåòàöèÿ ôîðìóëû Å, íà êîòî-
ðîé îíà ïðèíèìàåò ëîæíîå çíà÷åíèå, ò.å. |Å
*
|=F, è ïðîáóåì íàéòè
òàêóþ èíòåðïðåòàöèþ. Åñëè â ðåçóëüòàòå ïîëó÷àåì ïðîòèâîðå÷èå,
ýòî îçíà÷àåò, ÷òî òàêèõ èíòåðïðåòàöèé íå ñóùåñòâóåò, è, ñëåäîâà-
òåëüíî, ôîðìóëà ëîãè÷åñêè îáùåçíà÷èìà.
Ïðèìåðû.
1. Ðàññìîòðèì ôîðìóëó ∀õ(A(x)∨B)≡∀xA(x)∨B, ãäå B íå
çàâèñèò îò õ. Ïðåäïîëîæèì, ÷òî ñóùåñòâóåò òàêàÿ èíòåðïðåòàöèÿ,
íà êîòîðîé ôîðìóëà ëîæíà èìïëèêàöèÿ: |∀x(A*(x)∨
Β
*)→
→∀xA*(x)∨B*|=F. Ýòî âîçìîæíî, åñëè |∀x(A*(x)∨B*)|=T, à
|∀xA*(x)∨B
*
|=F. Èç ïîñëåäíåãî ðàâåíñòâà ñëåäóåò, ÷òî |B*|=F è
|∀x(A*(x))|=F. Åñëè |∀x(A*(x))|=F, òî ñóùåñòâóåò õîòÿ áû îäíî
çíà÷åíèå x=a, òàêîå, ÷òî |A*(a)|=F. Ôîðìóëà |∀x(A*(x)∨B*)|=T.
Íî â îáëàñòè èíòåðïðåòàöèè äàííîé ôîðìóëû ñóùåñòâóåò çíà÷åíèå
x=a, äëÿ êîòîðîãî |A*(a)|=F è |B*| =F. Âîçìîæíî, ÷òî ñóùåñòâóåò
äðóãîå çíà÷åíèå x=b, äëÿ êîòîðîãî |A*(b)|=T. Òîãäà |∀x(A*(x)∨B*)|=
∀
*( ) *
*( ) *
Aa B FF F
Ab B TFT
∨=∨=
∨=∨=
=F, ÷òî ïðîòèâîðå÷èò ïðåäïîëîæåíèþ
|(A*(x)∨B*)|=T.
Ïðîâåðèì âûïîëíåíèå äðóãîé èìïëèêàöèè. Ïðåäïîëîæèì, ÷òî
|∀xA*(x)∨B*→∀x(A*(x)∨B*)|=F. Òîãäà |∀x(A*(x)∨B*)|=F, è
|∀xA*(x)∨B*|=T. Èç |∀x(A*(x)∨B*)|=F ñëåäóåò, ÷òî ñóùåñòâóåò
òàêîå x=a, ÷òî |A
*
(a)∨B
*
|=F. Îòñþäà ñëåäóåò, ÷òî |A*(a)|=F,
|B*|=F. Ñëåäîâàòåëüíî, â îáëàñòè îïðåäåëåíèÿ ïðåäèêàòà À(x)
ñóùåñòâóåò çíà÷åíèå x=a, ïðè êîòîðîì ïðåäèêàò |À*(à)|=F, çíà÷èò,
|∀xA*(x)|=F. Òîãäà ôîðìóëà |∀xA*(x)∨F|=F, ÷òî ïðîòèâîðå÷èò
ïðåäïîëîæåíèþ. Ñëåäîâàòåëüíî, ôîðìóëà
∀õ(A(x)∨B)≡∀xA(x)∨B ëîãè÷åñêè îáùåçíà÷èìà.
2. Äîêàæåì, ÷òî ôîðìóëà (∀xP(x)→∀xQ(x)) → ∀x(P(x)→Q(x))íå
ÿâëÿåòñÿ ëîãè÷åñêè îáùåçíà÷èìîé. Ïðåäïîëîæèì, ÷òî íà íåêîòîðîé
èíòåðïðåòàöèè |(∀xP*(x)→∀xQ*(x)) → ∀x(P*(x)→Q*(x))| = F.
Òîãäà |(∀xP*(x)→∀xQ*(x))| = T è |∀x(P*(x)→Q*(x))| = F. Èç
ïîñëåäíåãî ñëåäóåò, ÷òî ñóùåñòâóåò òàêîå x=a, ÷òî |P*(a)→Q*(a)|=F,
îòêóäà |P*(a)| = T, |Q*(a)| = F. Òîãäà |∀xQ*(x))| = F, è, âîçìîæíî,
ñóùåñòâóåò òàêîå b, ÷òî |P*(b)| = F, òîãäà |∀xP*(x)| = F
è|(∀xP*(x)→∀xQ*(x))| = T. Ñëåäîâàòåëüíî, ñóùåñòâóåò òàêàÿ èí-
òåðïðåòàöèÿ, íà êîòîðîé ôîðìóëà ïðèíèìàåò ëîæíîå çíà÷åíèå.
12.5. Ëîãè÷åñêîå ñëåäîâàíèå â ëîãèêå ïðåäèêàòîâ
12.5.1. Îïðåäåëåíèå ëîãè÷åñêîãî ñëåäîâàíèÿ
Îïðåäåëåíèå 12.10. Ãîâîðÿò, ÷òî ôîðìóëà  ëîãè÷åñêè ñëåäóåò
èç ôîðìóëû À, åñëè â ëþáîé èíòåðïðåòàöèè, â êîòîðîé À
ïðèíèìàåò èñòèííîé çíà÷åíèå,  òàêæå ïðèíèìàåò èñòèííîå
çíà÷åíèå. Îáîçíà÷åíèå: A|= Â.
 îáùåì ñëó÷àå ôîðìóëà  ÿâëÿåòñÿ ëîãè÷åñêèì ñëåäñòâèåì
ìíîæåñòâà ôîðìóë Γ, åñëè îíà èñòèííà íà âñåõ òåõ èíòåðïðåòàöèÿõ,
íà êîòîðûõ âûïîëíåíû (èñòèííû îäíîâðåìåííî) âñå ôîðìóëû èçΓ.
Îïðåäåëåíèå 12.11. Ãîâîðÿò, ÷òî ôîðìóëà À ðàâíîñèëüíà, èëè
ëîãè÷åñêè ýêâèâàëåíòíà, ôîðìóëå Â, åñëè êàæäàÿ èç íèõ
ëîãè÷åñêè âëå÷åò äðóãóþ, ò.å. åñëè A |=  è B|=A. Îáîçíà÷åíèå:
À⇔Â.
Èç îïðåäåëåíèé ñëåäóþò óòâåðæäåíèÿ:
1. À |= Â òîãäà è òîëüêî òîãäà, êîãäà |=À→Â.
2. À
1
,..., A
n
|= B, òîãäà è òîëüêî òîãäà, êîãäà |=À
1
&...&A
n
→ B.
3. A ⇔ B òîãäà è òîëüêî òîãäà, êîãäà |= À ≡ Â.
4. Åñëè À |= Â è |À|=Ò, òî |Â|=Ò â íåêîòîðîé èíòåðïðåòàöèè.
5. Åñëè Ã |=Â è ∀i(|Ã
i
|=Ò), òî |Â|=Ò.
12.5.2. Îñíîâíûå ïðàâèëà âûâîäà ëîãèêè ïðåäèêàòîâ
Ðàññìîòðèì íåêîòîðûå ëîãè÷åñêèå ñëåäîâàíèÿ, êîòîðûå âûïîë-
íåíû â ëîãèêå ïðåäèêàòîâ. Êàæäîå òàêîå ëîãè÷åñêîå ñëåäîâàíèå
çàäàåò ïðàâèëî âûâîäà â ëîãèêå ïðåäèêàòîâ; íåêîòîðûå èç íèõ áóäóò
èñïîëüçîâàíû â ôîðìàëüíîé òåîðèè ïðåäèêàòîâ.
1. Ïðàâèëî óíèâåðñàëüíîé êîíêðåòèçàöèè (ÓÊ):
∀õÀ(õ)|=À(ó), åñëè ó ñâîáîäíî äëÿ õ â À(õ).
Äîêàçàòåëüñòâî. Íóæíî äîêàçàòü, ÷òî åñëè |∀xA*(x)|=T â
íåêîòîðîé èíòåðïðåòàöèè D, òî |A*(y)|=T â òîé æå èíòåðïðåòàöèè.
Äîïóñòèì |A*(y)|=F. Òîãäà ñóùåñòâóåò òàêîå b∈D, ÷òî |A*(b)|=F.
Òåîðèÿ ïðåäèêàòîâ ïåðâîãî ïîðÿäêàÃëàâà 12

212 213Òåîðèÿ ïðåäèêàòîâ ïåðâîãî ïîðÿäêàÃëàâà 12
Íî ïî óñëîâèþ ôîðìóëà |∀xA*(x)|=T íà D, à òàê êàê b∈D, òî
|∀xA*(x)|=F íà D. Ýòî ïðîòèâîðå÷èå äîêàçûâàåò òåîðåìó.
2. Ïðàâèëî ýêçèñòåíöèàëüíîé êîíêðåòèçàöèè (ÝÊ):
∃xA(x) |=A(b), ãäå b∈D.
Äîêàçàòåëüñòâî. Äîïóñòèì, |∃xA*(x)|=T â íåêîòîðîé
èíòåðïðåòàöèè D. Òîãäà ñóùåñòâóåò òàêîå b∈D, ÷òî |A*(b)|=T.
3. Ïðàâèëî ýêçèñòåíöèàëüíîãî îáîáùåíèÿ:
A(y) |= ∃xA(õ), ãäå õ ñâîáîäíî äëÿ y â A(ó).
Äîêàçàòåëüñòâî. Åñëè |A*(y)|=Ò â íåêîòîðîé èíòåðïðåòàöèè
D, òî ñóùåñòâóåò ó=b, b∈D, òàêîå ÷òî |A*(b)|=T. Ñëåäîâàòåëüíî,
|∃xA*(x)|=T â èíòåðïðåòàöèè D.
4. Ïðàâèëî âñåîáùíîñòè:
C → A(õ) |= C → ∀x(A(õ)),
åñëè C íå ñîäåðæèò ñâîáîäíûõ âõîæäåíèé õ.
Äîêàçàòåëüñòâî. Ïî óñëîâèþ |C → A*(x)|=T â èíòåðïðåòàöèè
D. Ýòî âîçìîæíî, åñëè
a) |C|=F, òîãäà |C→A*(x)|=T è |C→∀xA*(x)|=T;
á) |C|=T, |C → A*(x)|=T, ñëåäîâàòåëüíî, |A*(x)|=T â
èíòåðïðåòàöèè D äëÿ ëþáîãî õ, çíà÷èò |C → ∀xA*(x)|=T.
5. Ïðàâèëî ñóùåñòâîâàíèÿ:A(x) → C |= ∃xA(x) → C,
åñëè C íå ñîäåðæèò ñâîáîäíûõ âõîæäåíèé õ.
Äîêàçàòåëüñòâî. |A*(x) → C|=T â íåêîòîðîé èíòåðïðåòàöèè D.
Äîïóñòèì |∃xA*(x)→C|=F â èíòåðïðåòàöèè D. Òîãäà |C|=F, (C íå
çàâèñèò îò x) è |∃xA*(x)|=T, ñëåäîâàòåëüíî, ñóùåñòâóåò õ=b, òàêîå
÷òî |A*(b)|=T è |A*(b)→C|=F, â òî âðåìÿ êàê ïî óñëîâèþ
|A*(x)→C|=T. Ïîëó÷åííîå ïðîòèâîðå÷èå äîêàçûâàåò òåîðåìó.
6. Ïðàâèëî îáîáùåíèÿ Gen (îò àíãëèéñêîãî ñëîâà Generalization):
åñëè Γ |= À(õ), òî Γ |= ∀õA(õ), åñëè õ íå âõîäèò ñâîáîäíî íè â
îäíó èç ôîðìóë Γ.
Äîêàçàòåëüñòâî. Ïðåäïîëîæèì, âûáðàíà îáëàñòü èíòåðïðåòàöèè
D è ïðîèçâåäåíà çàìåíà â À âñåõ ñâîáîäíûõ ïåðåìåííûõ íà ýëåìåíòû
èç D, íàïðèìåð, õ=b∈D. Òîãäà |A*(b)|=T, òàê êàê |Γ
i
|=T äëÿ âñÿêîãî
i. Òàê êàê õ íå âõîäèò ñâîáîäíî íè â îäíó èç ôîðìóë Γ, òî â ìíîæåñòâå
Γ çàìåíû õ íà b íå áûëî è, ñëåäîâàòåëüíî, äëÿ ëþáîãî x∈D, òàêîãî
÷òî |A*(õ)|=Ò, Γ |= A*(õ), ñëåäîâàòåëüíî, Γ |=∀õA*(õ).
12.6. Èñ÷èñëåíèå ïðåäèêàòîâ ïåðâîãî ïîðÿäêà
12.6.1. Ôîðìàëüíàÿ òåîðèÿ K
Ïîñêîëüêó ïîñòðîåíèå òàáëèö èñòèííîñòè äëÿ ëþáîé ôîðìóëû
íå ïðåäñòàâëÿåòñÿ âîçìîæíûì äëÿ ïðîâåðêè îáùåçíà÷èìîñòè
ôîðìóë òåîðèè ïðåäèêàòîâ, àêñèîìàòè÷åñêèé ìåòîä íåîáõîäèì äëÿ
èññëåäîâàíèÿ ôîðìóë, ñîäåðæàùèõ êâàíòîðû. Ðàññìîòðèì ôîð-
ìàëüíóþ òåîðèþ ïåðâîãî ïîðÿäêà
1
K.
Ñèìâîëàìè òåîðèè K ñëóæàò òå æå ñèìâîëû ëîãèêè ïðåäèêàòîâ:
ïðîïîçèöèîíàëüíûå ñâÿçêè →, ¬, ∀, ∃, âñïîìîãàòåëüíûå ñèìâîëû
(, ), ìíîæåñòâà ïðåäìåòíûõ ïåðåìåííûõ: x
1
,x
2
,..., ïðåäìåòíûõ ïîñòî-
ÿííûõ: a
1
,a
2
,..., ôóíêöèîíàëüíûå ñèìâîëû: f
i
n
, i=1,,k, n=0,,m,
ïðåäèêàòíûå ñèìâîëû: P
i
n
, i=1, , k, n=0, , m. Îïðåäåëåíèÿ
òåðìà, ôîðìóëû è ïðîïîçèöèîíàëüíûõ ñâÿçîê &, ∨, ≡ îñòàþòñÿ â
ñèëå äëÿ òåîðèè ïåðâîãî ïîðÿäêà.
Àêñèîìû òåîðèè K ðàçáèâàþòñÿ íà ëîãè÷åñêèå àêñèîìû è
ñîáñòâåííûå.
Ëîãè÷åñêèå àêñèîìû. Êàêîâû áû íè áûëè ôîðìóëû À, Â, Ñ
òåîðèè K, ñëåäóþùèå ôîðìóëû ÿâëÿþòñÿ ëîãè÷åñêèìè àêñèî-
ìàìè òåîðèè K.
À1 À → (Â → À).
À2 (À → (Â → Ñ)) → ((À → Â) → (À → Ñ).
À3 (¬Â → ¬À) → ((¬Â → À) → Â).
À4 ∀õÀ(õ) → À(y), åñëè ó ñâîáîäíî äëÿ õ â ôîðìóëå À(õ).
À5 ∀õ(À → Â(õ)) → (À → ∀õÂ(õ)), åñëè À íå ñîäåðæèò ñâîáîä-
íûõ âõîæäåíèé õ.
Ñîáñòâåííûå àêñèîìû ôîðìóëèðóþòñÿ îòäåëüíî äëÿ êàæäîé
êîíêðåòíîé ñîäåðæàòåëüíîé ïðåäìåòíîé îáëàñòè.
Ïðàâèëàìè âûâîäà âî âñÿêîé òåîðèè ïåðâîãî ïîðÿäêà ÿâëÿþòñÿ:
1) modus ponens (ÌÐ): èç À è À → Â ñëåäóåò Â,
2) ïðàâèëî îáîáùåíèÿ Gen: èç Γ |= À(õ), ñëåäóåò Γ |= ∀õA(õ),
åñëè õ íå âõîäèò ñâîáîäíî íè â îäíó èç ôîðìóë Γ.
Òåîðèÿ K, íå ñîäåðæàùàÿ ñîáñòâåííûõ àêñèîì, íàçûâàåòñÿ èñ÷èñ-
ëåíèåì ïðåäèêàòîâ ïåðâîãî ïîðÿäêà.
Ìîäåëüþ òåîðèè ïåðâîãî ïîðÿäêà K íàçûâàåòñÿ âñÿêàÿ èíòåð-
ïðåòàöèÿ, â êîòîðîé èñòèííû âñå àêñèîìû òåîðèè K. Åñëè ïðàâèëà
âûâîäà ÌÐ è Gen ïðèìåíÿþòñÿ ê èñòèííûì â äàííîé èíòåðïðå-
òàöèè ôîðìóëàì, òî ðåçóëüòàòîì ÿâëÿþòñÿ ôîðìóëû, òàêæå èñòèí-
íûå â òîé æå èíòåðïðåòàöèè. Ñëåäîâàòåëüíî, âñÿêàÿ òåîðèÿ K èñòèí-
íà âî âñÿêîé åå ìîäåëè.
1
 òåîðèÿõ ïåðâîãî ïîðÿäêà íå äîïóñêàåòñÿ íàâåøèâàíèå êâàíòîðîâ ïî ïðåäè-
êàòàì èëè ïî ôóíêöèÿì è íå èñïîëüçóþòñÿ ïðåäèêàòû, èìåþùèå â êà÷åñòâå
çíà÷åíèé ñâîèõ àðãóìåíòîâ äðóãèå ïðåäèêàòû. Òàêèå êîíñòðóêöèè ðàññìàòðèâà-
þòñÿ â òåîðèÿõ ïðåäèêàòîâ áîëåå âûñîêèõ ïîðÿäêîâ.

214 215Òåîðèÿ ïðåäèêàòîâ ïåðâîãî ïîðÿäêàÃëàâà 12
Ìíîæåñòâî ôîðìóë, âûâîäèìûõ ïî ïðàâèëàì âûâîäà èç àêñèîì
òåîðèè K, ÿâëÿåòñÿ òåîðåìàìè òåîðèè K. Àêñèîìû À1, À2, À3 òåîðèè
K è ïðàâèëî ÌÐ îïðåäåëåíû â òåîðèè L, ñëåäîâàòåëüíî, âñå òåîðåìû
òåîðèè L âêëþ÷åíû â ìíîæåñòâî òåîðåì òåîðèè K.
Ìåòàòåîðåìà î äåäóêöèè â òåîðèè K ìîæåò áûòü ñôîðìóëèðî-
âàíà â îñëàáëåííîì âèäå.
Ìåòàòåîðåìà î äåäóêöèè. Åñëè ñóùåñòâóåò âûâîä ôîðìóëû Â
èç ìíîæåñòâà ãèïîòåç Γ è ôîðìóëû À: Γ, À |Â, è â ýòîì âûâîäå
íè ïðè êàêîì ïðèìåíåíèè ïðàâèëà Gen ê ôîðìóëàì, çàâèñÿùèì
îò À, íå ñâÿçûâàåòñÿ êâàíòîðîì íèêàêàÿ ñâîáîäíàÿ ïåðåìåííàÿ
ôîðìóëû À, òî Γ |À→Â.
Ñëåäñòâèå 1. Åñëè ñóùåñòâóåò âûâîä Γ, À | Â, è â ýòîì âûâîäå
íè ðàçó íå ïðèìåíÿëîñü ïðàâèëî Gen ê ôîðìóëàì, çàâèñÿùèì
îò À, òî Γ| À → Â.
Ñëåäñòâèå 2. Åñëè ñóùåñòâóåò âûâîä Γ, À | Â, ãäå À çàìêíóòàÿ
ôîðìóëà, òî Γ | À → Â.
12.6.2. Òåîðèÿ ïåðâîãî ïîðÿäêà ñ ðàâåíñòâîì
Ðàññìîòðèì òåîðèþ ïåðâîãî ïîðÿäêà K, â ÷èñëå ïðåäèêàòíûõ
ñèìâîëîâ êîòîðîé ñîäåðæèòñÿ ïðåäèêàò ðàâåíñòâà À
1
2
(t, s), êîòîðûé
äëÿ ñîêðàùåíèÿ áóäåì îáîçíà÷àòü t = s, à âìåñòî ¬À
1
2
(t,s) ñîîòâåò-
ñòâåííî áóäåì ïèñàòü t ≠ s.
Îïðåäåëåíèå 12.12. Òåîðèÿ K íàçûâàåòñÿ òåîðèåé ïåðâîãî ïî-
ðÿäêà ñ ðàâåíñòâîì, åñëè ñëåäóþùèå ôîðìóëû ÿâëÿþòñÿ òåîðå-
ìàìè òåîðèè K:
À6. ∀õ
1
(õ
1
= õ
1
)(ðåôëåêñèâíîñòü ðàâåíñòâà);
À7. (õ = y) → (À(x, x) → À(x, y)) (ïîäñòàíîâî÷íîñòü
ðàâåíñòâà),
ãäå õ, y ïðåäìåòíûå ïåðåìåííûå, À(x, x) ïðîèçâîëüíàÿ
ôîðìóëà, À(x, y) ïîëó÷àåòñÿ çàìåíîé êàêèõ-íèáóäü (íå îáÿçà-
òåëüíî âñåõ) ñâîáîäíûõ âõîæäåíèé x íà y, åñëè y ñâîáîäíî äëÿ
òåõ âõîæäåíèé x, êîòîðûå çàìåíÿþòñÿ.
Äîêàæåì îñíîâíûå òåîðåìû òåîðèè ïåðâîãî ïîðÿäêà ñ ðàâåíñòâîì.
Òåîðåìà 12.1. | t = t äëÿ ëþáîãî òåðìà t.
Äîêàçàòåëüñòâî. Èç À6: | ∀õ
1
(õ
1
= õ
1
) ïî ïðàâèëó óíèâåðñàëü-
íîé êîíêðåòèçàöèè ïîëó÷àåì | t = t.
Òåîðåìà 12.2. | õ = y → y = õ.
Äîêàçàòåëüñòâî. Ïóñòü À(x, x) åñòü õ = õ, À(x, y) åñòü y = õ.
Òîãäà:
| (õ = y) → (õ = õ → y = õ) ñîãëàñíî À7;
| õ = õ ñîãëàñíî òåîðåìå 12.1;
| õ = y → y = x ïî ïðàâèëó óäàëåíèÿ
ñðåäíåé ïîñûëêè.
Òåîðåìà 12.3. | õ = y → (y = z → õ = z).
Äîêàçàòåëüñòâî. Ïóñòü À(y, y) åñòü y = z, À(y, x) õ = z.
Òîãäà, çàìåíèâ õ íà y è y íà õ, ïîëó÷èì:
| (y = x) → (y = z → õ = z) ñîãëàñíî À7;
| õ = y → y = x ñîãëàñíî òåîðåìå 12.2;
| õ = y → (y = z → õ = z) ïî ïðàâèëó ñèëëîãèçìà.
12.7. Äîêàçàòåëüñòâî ëîãè÷åñêèõ ñëåäîâàíèé
âëîãèêå ïðåäèêàòîâ
12.7.1. Ôîðìàëèçàöèÿ ïðåäëîæåíèé åñòåñòâåííîãî ÿçûêà
ßçûê ëîãèêè ïðåäèêàòîâ òðàäèöèîííî ñëóæèò äëÿ ôîðìàëèçà-
öèè âûñêàçûâàíèé åñòåñòâåííîãî ÿçûêà.
Ïðèìåð. Ðàññìîòðèì îáëàñòü îïðåäåëåíèÿ Ì={ëþäè} ñ çàäàí-
íûìè íà íåé ïðåäèêàòàìè: J(x): õ ñóäüÿ; L(x): õ þðèñò; S(x):
õ æóëèê; A(x,y): x ëþáèò ó.
Ïîíÿòèå «þðèñò» ìîæíî îïðåäåëèòü êàê ìíîæåñòâî âñåõ ëþäåé,
èìåþùèõ þðèäè÷åñêîå îáðàçîâàíèå. Ïîíÿòèå «ñóäüÿ» ìîæíî îïðå-
äåëèòü êàê ìíîæåñòâî ëþäåé, èìåþùèõ þðèäè÷åñêîå îáðàçîâàíèå,
ðàáîòàþùèõ â ñóäå è âûïîëíÿþùèõ âïîëíå îïðåäåëåííûå îáÿçàííî-
ñòè. Òàêèì îáðàçîì, ìíîæåñòâî ñóäåé ÿâëÿåòñÿ ïîäìíîæåñòâîì ìíî-
æåñòâà þðèñòîâ, ò.å. ñâîéñòâî áûòü ñóäüåé âëå÷åò ñâîéñòâî áûòü
þðèñòîì, è îáëàñòü èñòèííîñòè ïðåäèêàòà J âêëþ÷åíà â îáëàñòü
èñòèííîñòè ïðåäèêàòà L (ñì. ðèñ.12.3), ò.å. ñïðàâåäëèâî âûñêàçûâà-
íèå: êàæäûé ñóäüÿ ÿâëÿåòñÿ þðèñòîì, ÷òî ìîæíî âûðàçèòü â âèäå
ôîðìóëû: ∀x(J(x)→L(x)).
Ðèñ. 12.3. Îáëàñòè îïðåäåëåíèÿ ïðåäèêàòîâ.
Ðàññìîòðèì âûñêàçûâàíèå: «Íåêîòîðûå þðèñòû æóëèêè». Ýòî
âûñêàçûâàíèå èñòèííî, åñëè ñóùåñòâóþò òàêèå îáúåêòû, êîòîðûå
ÿâëÿþòñÿ îäíîâðåìåííî è þðèñòàìè, è æóëèêàìè: ∃x(L(x)&S(x)),
ò.å. îáëàñòè èñòèííîñòè ïðåäèêàòîâ L(x)èS(x) ïåðåñåêàþòñÿ: L∩S.
Ñëåäóåò ëè èç ýòîãî, ÷òî ñóùåñòâóþò ñóäüè-æóëèêè? Íåò, íå ñëåäóåò.

216 217Òåîðèÿ ïðåäèêàòîâ ïåðâîãî ïîðÿäêàÃëàâà 12
Îáëàñòè èñòèííîñòè ïðåäèêàòîâ J(x) è S(x) ìîãóò ïåðåñåêàòüñÿ
(ðèñ.12.3, á), à ìîãóò è íå ïåðåñåêàòüñÿ (ðèñ.12.3, à). Ìû ìîãëè áû
ñêàçàòü: «Âîçìîæíî, ñóùåñòâóþò ñóäüè-æóëèêè», îäíàêî êàòåãîðèþ
âîçìîæíîñòè íåëüçÿ âûðàçèòü â òåîðèè ïðåäèêàòîâ 1-ãî ïîðÿäêà.
Ôîðìàëèçóåì íåêîòîðûå äðóãèå âûñêàçûâàíèÿ:
∃x(S(x)&∀y(L(y)→À(x,y))) íåêîòîðûå æóëèêè ëþáÿò
âñåõ þðèñòîâ;
∃x(S(x)&∀y(A(x,y)→L(y))) íåêîòîðûå æóëèêè ëþáÿò
òîëüêî þðèñòîâ;
∃x(S(x)&∃y(L(y)&A(x,y))) íåêîòîðûå æóëèêè ëþáÿò
íåêîòîðûõ þðèñòîâ;
∀x(S(x)→∀y(J(y)→¬A(x,y))) âñå æóëèêè íå ëþáÿò ñóäåé.
12.7.2. Îñíîâíûå ñõåìû ñóæäåíèé
 òðàäèöèîííîé ëîãèêå îáû÷íî âûäåëÿþò ÷åòûðå îñíîâíûõ ñõå-
ìû ñóæäåíèé.
1).Îáùåóòâåðäèòåëüíîå ñóæäåíèå: A: Âñå S ñóòü P: ∀x(S(x)→P(x)).
Ïðèìåð. Â ïîñëåäóþùèõ ïðèìåðàõ ïóñòü x ∈ {ëþäè}, y∈{ïðî-
èçâåäåíèÿ}. Íà ýòèõ îáëàñòÿõ çàäàíû ïðåäèêàòû: P(x): x ïèñàòåëü,
V(x): x ïîýò, W(x, y): x ïèøåò y, N(y): y ðîìàí, K(y): y êîíñïåêò,
C(y): y ñòèõè, U(y): y ó÷åáíèê. Ðàññìîòðèì äâà ïîíÿòèÿ:
«ó÷åáíèêè» è «êîíñïåêòû». Ïîíÿòèå «ó÷åáíèêè» îáëàäàåò òåì ñâîé-
ñòâîì, ÷òî ýòî êíèãè, ïî êîòîðûì ó÷àòñÿ. Ïðåäèêàò U(x) ñðåäè
âñåõ êíèã âûäåëÿåò òå, êîòîðûå ÿâëÿþòñÿ ó÷åáíèêàìè. Ïî êîíñïåê-
òàì òàêæå ó÷àòñÿ, îäíàêî, êîíñïåêòû îáëàäàþò åùå è òåì ñâîéñòâîì,
÷òî îíè íàïèñàíû îò ðóêè. Ïîýòîìó êîíñïåêòû ìîæíî ñ÷èòàòü ïîä-
ìíîæåñòâîì ó÷åáíèêîâ (ñì. ðèñ. 12.4). Îòñþäà ñëåäóåò, ÷òî «êàæäûé
êîíñïåêò ÿâëÿåòñÿ ó÷åáíèêîì», èëè «âñå êîíñïåêòû ó÷åáíèêè»,
÷òî âûðàæàåòñÿ ôîðìóëîé: ∀x(K(x)→U(x)).
Ðèñ. 12.4. ∀x(K(x)→U(x)) Âñå êîíñïåêòû ó÷åáíèêè.
2). Îáùåîòðèöàòåëüíîå ñóæäåíèå: E: Íè îäíî S íå ñóòü P:
∀x(S(x)→¬P(x)).
Ïðèìåð. Ðàññìîòðèì äâà ïîíÿòèÿ: «êîíñïåêòû» è «ðîìàíû».
Î÷åâèäíî, ÷òî îáëàñòè èñòèííîñòè ýòèõ ïðåäèêàòîâ íå ïåðåñåêàþòñÿ
(ñì. ðèñ. 12.5), ò.å. «íè îäèí êîíñïåêò íå ÿâëÿåòñÿ ðîìàíîì», ÷òî
âûðàæàåòñÿ ôîðìóëîé: ∀x(K(x)→¬N(x)).
Ðèñ. 12.5. ∀x(K(x)→¬N(x))
Íè îäèí êîíñïåêò íå ÿâëÿåòñÿ ðîìàíîì.
3). ×àñòíîóòâåðäèòåëüíîå ñóæäåíèå: I: Íåêîòîðûå S ñóòü P
∃x(S(x)&P(x)).
Ïðèìåð. Ïîíÿòèÿ «ðîìàíû» è «ñòèõè» èìåþò ïåðåñåêàþùèåñÿ
îáúåìû (ðèñ.12.6), êàê èçâåñòíî, ñóùåñòâóþò ðîìàíû â ñòèõàõ,
íàïðèìåð, «Åâãåíèé Îíåãèí». Óòâåðæäåíèå «íåêîòîðûå ðîìàíû
íàïèñàíû â ñòèõàõ» âûðàæàåòñÿ ôîðìóëîé: ∃x(N(x)&C(x)).
Ðèñ. 12.6. ∃x(N(x) & C(x)) Íåêîòîðûå ðîìàíû ñòèõè.
4). ×àñòíîîòðèöàòåëüíîå ñóæäåíèå: O: Íåêîòîðûå S íå ñóòü P:
∃x(S(x)&¬P(x)).
Ïðèìåð. Ðàññìîòðèì óòâåðæäåíèÿ: «íåêîòîðûå ðîìàíû íå
ñòèõè»: ∃x(N(x)&¬C(x)), «íåêîòîðûå êîíñïåêòû íå ðîìàíû»:
∃x(K(x)&¬N(x)). Îáëàñòè èñòèííîñòè ñîîòâåòñòâóþùèõ ïðåäèêà-
òîâ ìîãóò ïåðåñåêàòüñÿ, à ìîãóò è íå ïåðåñåêàòüñÿ (ñì. ðèñ. 12.7).
Ðèñ. 12.7. ∃x(N(x) & ¬C(x)) Íåêîòîðûå ðîìàíû íå ñòèõè;
∃x(K(x) & ¬N(x)) Íåêîòîðûå êîíñïåêòû íå ðîìàíû.
Ýòè ÷åòûðå òèïà ñóæäåíèé îáðàçóþò òàê íàçûâàåìûé ëîãè÷åñêèé
êâàäðàò, êîòîðûé ïîêàçûâàåò ñâÿçü ìåæäó ñõåìàìè ñóæäåíèé (ðèñ.12.8).
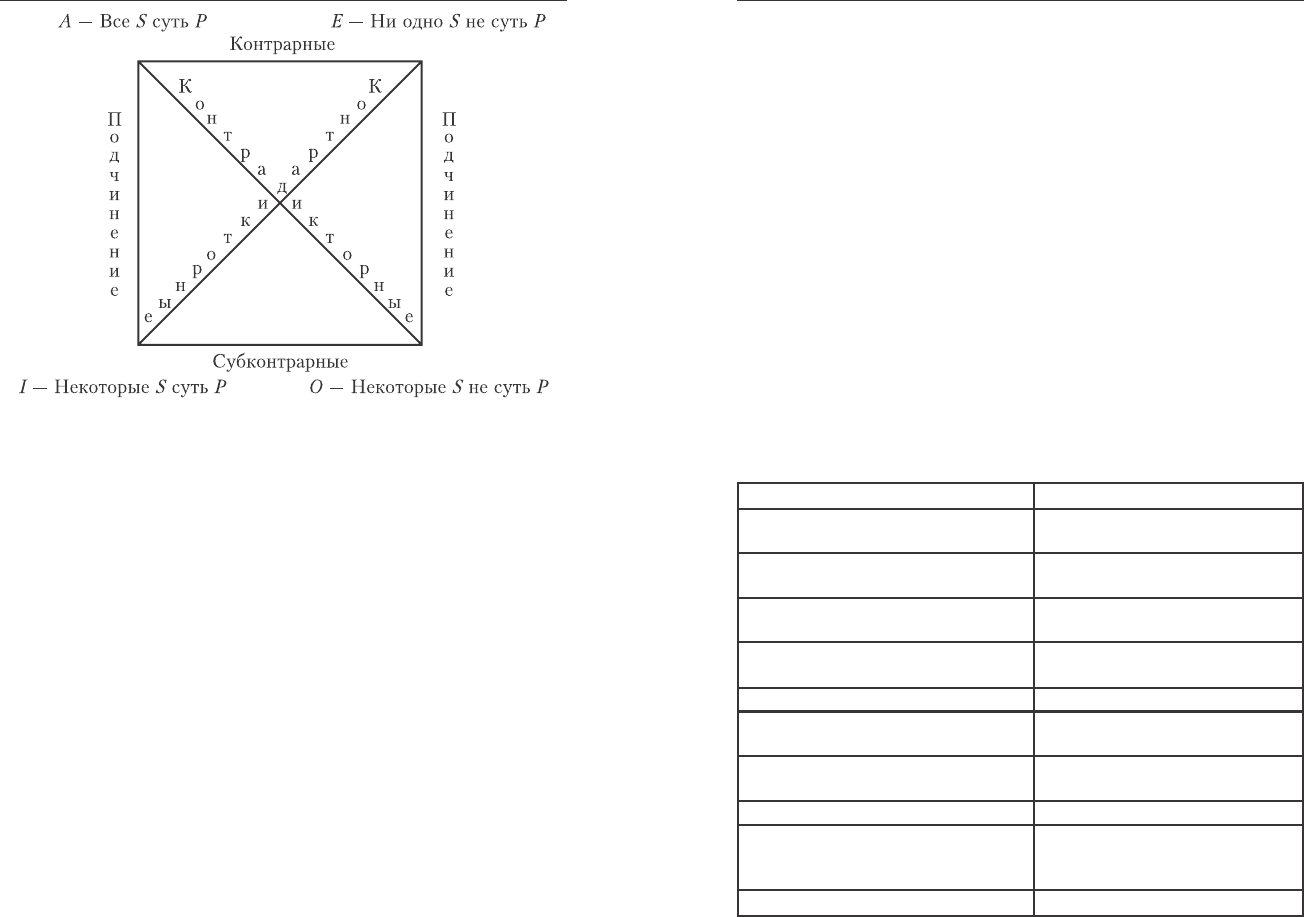
218 219
Ðèñ. 12.8. Ëîãè÷åñêèé êâàäðàò.
Ñóæäåíèÿ, ñîåäèíåííûå äèàãîíàëÿìè, íàçûâàþòñÿ êîíòðàäèê-
òîðíûìè. Êîíòðàäèêòîðíûå óòâåðæäåíèÿ íåñîâìåñòèìû ïî èñòèí-
íîñòè è íåñîâìåñòèìû ïî ëîæíîñòè, ò.å. íå ìîãóò áûòü îäíîâðåìåííî
èñòèííûìè, è íå ìîãóò áûòü îäíîâðåìåííî ëîæíûìè. Îäíî ÿâëÿ-
åòñÿ îòðèöàíèåì äðóãîãî:
1) ¬A = O, ò.å. «íå âñå S ñóòü P» ≡ «íåêîòîðûå S íå ñóòü P».
Äåéñòâèòåëüíî: ¬∀x(S(x)→P(x)) ≡ ∃x¬(¬S(x)∨P(x)) ≡
≡∃x(S(x)&¬P(x)). Íàïðèìåð, ∀x(N(x)→C(x)) («âñå ðîìàíû
íàïèñàíû â ñòèõàõ» è ∃x(N(x)&¬C(x)) («íåêîòîðûå ðîìàíû íå
ñòèõè») êîíòðàäèêòîðíûå óòâåðæäåíèÿ, îäíî ÿâëÿåòñÿ îòðèöà-
íèåì äðóãîãî.
2) ¬E = I , ò.å. «íåâåðíî, ÷òî íè îäíî S íå ñóòü P» ≡ «íåêîòîðûå
S ñóòü P».
¬∀x(S(x)→¬P(x)) ≡ ∃x¬(¬S(x)∨¬P(x)) ≡ ∃x(S(x)&P(x)).
Ãîðèçîíòàëüíûå ñòîðîíû êâàäðàòà ïîêàçûâàþò îòíîøåíèÿ êîíò-
ðàðíîñòè è ñóáêîíòðàðíîñòè. Óòâåðæäåíèÿ A: Âñå S ñóòü P:
∀x(S(x)→P(x)) è E: Íè îäíî S íå ñóòü P : ∀x(S(x)→¬P(x))
íàçûâàþòñÿ êîíòðàðíûìè. Îíè ñîâìåñòèìû ïî ëîæíîñòè, íî íåñîâ-
ìåñòèìû ïî èñòèííîñòè, ò.å. ìîãóò áûòü îäíîâðåìåííî ëîæíûìè,
íî íå ìîãóò áûòü îäíîâðåìåííî èñòèííûìè. Íàïðèìåð, «âñå ðîìàíû
íàïèñàíû â ñòèõàõ»: ∀x(N(x)→C(x)) è «íè îäèí ðîìàí íå íàïèñàí
â ñòèõàõ»: ∀x(N(x)→¬C(x)), êîíòðàðíûå óòâåðæäåíèÿ; îáà îíè
ëîæíû. Óòâåðæäåíèÿ: «âñå ëþäè ñìåðòíû» è «âñå ëþäè áåññìåðò-
íû», òàêæå êîíòðàðíû, ïåðâîå èñòèííî, âòîðîå ëîæíî.
Òåîðèÿ ïðåäèêàòîâ ïåðâîãî ïîðÿäêàÃëàâà 12
Óòâåðæäåíèÿ I: Íåêîòîðûå S ñóòü P: ∃x(S(x)&P(x)) è O: Íåêî-
òîðûå S íå ñóòü P: ∃x(S(x)&¬P(x)) íàçûâàþòñÿ ñóáêîíòðàðíûìè.
Ñóáêîíòðàðíûå óòâåðæäåíèÿ ñîâìåñòèìû ïî èñòèííîñòè, íî
íåñîâìåñòèìû ïî ëîæíîñòè, ò.å. ìîãóò áûòü îäíîâðåìåííî èñòèí-
íûìè, íî íå ìîãóò áûòü îäíîâðåìåííî ëîæíûìè. Íàïðèìåð, «íåêî-
òîðûå ðîìàíû ñòèõè»: ∃x(N(x)&C(x)) è «íåêîòîðûå ðîìàíû íå
ñòèõè»: ∃x(N(x)&¬C(x)), ñóáêîíòðàðíû; îáà îíè èñòèííû.
Âåðòèêàëüíûå ñòîðîíû êâàäðàòû ïîêàçûâàþò îòíîøåíèå ëîãè-
÷åñêîãî ñëåäîâàíèÿ (â ëîãè÷åñêîì êâàäðàòå îòíîøåíèå ïîä÷èíå-
íèÿ): óòâåðæäåíèÿ, íàõîäÿùèåñÿ ñíèçó, ëîãè÷åñêè ñëåäóþò èç òåõ,
÷òî íàõîäÿòñÿ ñâåðõó. Äåéñòâèòåëüíî, åñëè «âñå S ñóòü P», òî è
«íåêîòîðûå S ñóòü P», ò.å. âûïîëíåíî ëîãè÷åñêîå ñëåäîâàíèå:
∀x(S(x)→P(x)) |= ∃x(S(x)&P(x)), îòêóäà ñëåäóåò, ÷òî |A→ I| ≡ T.
Íàïðèìåð, åñëè «âñå êîíñïåêòû - ó÷åáíèêè», òî è «íåêîòîðûå
êîíñïåêòû ó÷åáíèêè». Äðóãîå ëîãè÷åñêîå ñëåäîâàíèå òàêæå
î÷åâèäíî: åñëè «íè îäíî S íå ñóòü P», òî è «íåêîòîðûå S íå ñóòü
P»: ∀x(S(x)→¬P(x)) |= ∃x(S(x)&¬P(x)), îòêóäà ñëåäóåò, ÷òî
|E→O| ≡ T. Íàïðèìåð, åñëè «íè îäèí ó÷åáíèê íå íàïèñàí â ñòèõàõ»,
òî è «íåêîòîðûå ó÷åáíèêè íå íàïèñàíû â ñòèõàõ».
Äðóãèå ïðèìåðû ôîðìàëèçàöèè âûñêàçûâàíèé ïðèâåäåíû â
òàáëèöå 12.6.
Òàáëèöà 12.6.
Âñå êîíñïåêòû ó÷åáíèêè. ∀y(K(y)→U(y))
Êîíñïåêò ïî ìàòåìàòèêå
(Ì) ó÷åáíèê. K(Ì)→U(Ì)
Íè îäèí ó÷åáíèê íå íàïèñàí
â ñòèõàõ. ∀y(U(y) → ¬C(y))
Íåêîòîðûå ðîìàíû íàïèñàíû
â ñòèõàõ. ∃y(N(y)&C(y))
«Åâãåíèé Îíåãèí» ýòî ðîìàí
â ñòèõàõ. N(Å.Îíåãèí.)&C(Å.Îíåãèí.)
Âñå ïîýòû ïèøóò ñòèõè. ∀x(V(x) → ∀y(C(y) → W(x,y)))
Íåêîòîðûå ïèñàòåëè ïèøóò
òîëüêî ðîìàíû. ∃x(P(x)&∀y(W(x,y) → N(y)))
Ïèñàòåëü Ëåâ Òîëñòîé ïèñàë P(Òîëñòîé)&
òîëüêî ðîìàíû. ∀y(W(Òîëñòîé,y) → N(y))
Êàæäûé ÷òî-íèáóäü ïèøåò. ∀x∃yW(x,y)
Êàæäûé, êòî ïèøåò ÷òî-íèáóäü,
ïèøåò ïîçäðàâëåíèå ∀x(∃yW(x,y)→W(x,NY))
ñ Íîâûì ãîäîì (NY).
Íåêîòîðûå ëþäè íè÷åãî íå ïèøóò. ∃x∀y¬W(x,y)
