Troyan V., Kiselev Y. Statistical Methods of Geophysical Data Processing

Подождите немного. Документ загружается.

Models of measurement data 103

The classical model of a linear regression can be obtained as a particular case of

(3.1), with a linear dependence of the model on the desired vector of the parameters:

u(x

, y

, z

, t

) =

j=0

, y

, z

, t

) + ε(x

, y

, z

, t

). (3.8)

The formula (3.8) can be considered as a basis of four dimensional space re-

gression, which is applicable at a numerical realization of the ray method. At the

processing of the geophysical data at present time three dimensional spatial model

and the three dimensional space-time model are widespread:

u(x

, y

, z

) =

j=0

, y

, z

) + ε(x

, y

, z

), (3.9)

u(x

, y

, t

) =

j=0

, y

, t

) + ε(x

, y

, t

). (3.10)

The formula (3.9) is used for the description of a formation velocity, values

of magnetic and gravitational ﬁelds at an areal spread on a ground surface. The

expression (3.10) is applied as a model of a seismic trace, thus function ψ(x

, t

)

describes the shape of a signal with unknown moments of the arrival θ

In the geophysical practice one-dimensional models are widespread

u(x

) =

j=0

) + ε(x

), (3.11)

u(t

) =

j=0

) + ε(t

). (3.12)

The formula (3.11) is used, for example, for the velocity smoothing in CDP or

seismic horizon smoothing along a proﬁle of observations. The representation (3.12)

is an initial model of a seismic trace for a great number of processing algorithms,

such as the predictive deconvolution and adaptive ﬁltration. In the matrix-vector

form the formulas (3.11), (3.12) look like

u = ψθ +

ε. (3.13)

For example, in the case of the model (3.11) the vectors

u and ε have the components

uu = [u

, . . . u

], ε = [ε

, . . . , ε

ψ =





. . . ψ

. . . . . . . . .

. . . ψ





The matrix ψ is called a design matrix.

104 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

3.4 The Models of Qualitative Interpretation

If as a result of the interpretation a geophysicist can obtain the information only

about a qualitative state of a target object, the appropriate model of experimental

data is called as a model of qualitative interpretation:

u(x

, y

, z

, t

)

ν = 1, 2, . . . , N











either f

, y

, z

, t

, θ) + ε(x

, y

, z

, t

or f

, y

, z

, t

, θ) + ε(x

, y

, z

, t

. . . . . .

or f

, y

, z

, t

θ) + ε(x

, y

, z

, t

(3.14)

where f

, y

, z

, t

, θ) is a ﬁeld of the idealized object of the investigation with

a state with a number ν = 1, 2, . . . , N . As an example we can consider a problem

of the detection of a seismic signal with the noise background using an area of a

seismic trace

u(t

) =



either Aϕ(t

− τ) + ε(t

or ε(t

(3.15)

where A, τ are known signal parameters (Fig. 3.3).

Fig. 3.3 Qualitative interpretation (either “signal and noise” or “noise”).

In the case of a choice between two signals we have (see Fig. 3.4)

u(t

) =



either A

ϕ(t

− τ

) + ε(t

or A

ϕ(t

− τ

) + ε(t

(3.16)

Fig. 3.4 Qualitative interpretation (“signal (A

) and nose” or “signal (A

) and noise”).

The important class of problems of the resolution of seismic signals is founded

on the following model of a seismogram (Fig. 3.5)

u(t

) =



either A

− τ

) + ε(t

or A

− τ

) + A

− τ

) + ε(t

(3.17)

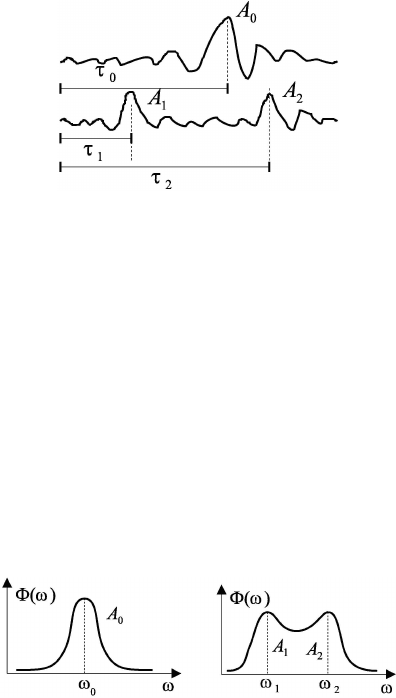
Models of measurement data 105

Fig. 3.5 Qualitative interpretation (either “signal (A

) and noise” or “two signals (A

and A

)

and noise”).

The statistical hypothesis test will allow to establish (with a given signiﬁcance

level) consistency of hypothesis that on the given interval of a seismogram there is

only one wave or, this hypothesis is rejected.

The statistical hypothesis test can be applied also to the spectral representa-

tion of a seismogram. In this case the problem consists in the examination of the

resolution at the separation of two spectral lines:

u(ω) =



either A

(ω − ω

) + E(ω),

or A

(ω − ω

) + A

(ω − ω

) + E(ω),

(3.18)

where ω

, ω

is a frequency delays, which determine a location of the signals

, Φ

(Fig. 3.6).

Fig. 3.6 Qualitative interpretation in the frequency domain (either “signal (A

) and noise” or

“two signals (A

and A

) and noise”).

3.5 The Models of Qualitative-Quantitative Interpretation

At the solution of composite interpretation problems of a modern geophysics the

investigator deals with models of a type

u(x

, y

, z

, t

)

ν = 1, 2, . . . , N











eitherf

, y

, z

, t

, θ

) + ε(x

, y

, z

, t

or f

, y

, z

, t

, θ

) + ε(x

, y

, z

, t

. . . . . .

or f

, y

, z

, t

, θ

) + ε(x

, y

, z

, t

(3.19)

where the state of an interesting object is characterized by N various deterministic

components f

(ν = 1, . . . , N), each of which depends on the vector θ

of unknown

106 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

parameters with components θ

νs

(s = 1, . . . , S). The problem consists in ﬁnding an

optimum procedure of a choice among probable states and an estimation of unknown

parameters on a given experimental material. The competing states of the object,

for which the models of an experimental material are under the construction, should

form a complete system of alternative (incompatible) events.

Let’s note, that at the formalization of the model of an experimental material

it is necessary to determine properties of a probability distribution of a random

component of the model, that can be implemented on the basis of available a priori

data.

3.6 Random Components of Model and its Properties

The properties of a random component ε in surveyed above models substantially

determine the structure of algorithms of a ﬁnding of an estimate of required param-

eters. Therefore at processing of a real geophysical material it is necessary carefully

to explore properties of a random component of the model. Let’s consider the vari-

ants of the representation of a random component having the greatest practical

interest at the solution of approximation problems of the geophysical data.

The central place at the determination of properties of a random component

is a choice of its distribution law. The geophysical noise ﬁeld has a composite

character and it formed by the great number of the independent factors. So, for

example, at the description of a seismic ﬁeld the random component of the model

can conventionally divide on the following basic components.

• Noise, which is connected with the passage of a signal through the seismic channel.

• Microseism is a weak oscillation of the ground determined by a state of a sur-

rounding environment. The level of the microseism is determined by meteorologi-

cal conditions, the motion of a transport, and also series of the geological factors;

for example, the water-saturated sedimentary rock produces 100 – 1000 times

greater noise than the solid basement rock.

• The assembly of a partial regular and not enough extended waves formed owing to

an inhomogeneity of the medium, an inclusion, a roughness of seismic interfaces,

and also the great number of multiple and partial multiple waves with a small

energy create the complex interference and irregular ﬁeld of a seismogram. This

ﬁeld it is permissible to consider as a sampling of some random function. Taking

into account a physical nature of the noise, it is possible, basing on the central

limit theorem, which proves an asymptotic normality of the sum of independent

random quantities to make the guess about the normality of a random component.

It is necessary to note, that at an increasing of a number of observations the

majority of distributions tend to the normal distribution (Student’s distribution,

binomial etc.). If it is known the ﬁrst two moments — (mathematical expectation

and variance σ

) only, the maximum entropy principle, which leads to the solution

Models of measurement data 107

of a variation problem with constraints, gives a normal distribution.

We write an explicit form for a random vector, which belongs to the normal

distribution ε = [ε

, . . . , ε

p(ε

ε) = (2π)

−n/2

|R|

−1/2

exp



−

(ε

ε −ε

)

−1

(

ε −ε

)



, (3.20)

where T is a sign of the transposition, ε

is a vector of the mathematical expectations

R is a covariance matrix with elements R

, |R| is a determinant of the covariance

matrix, R

−1

is an inverse covariance matrix. The main diagonal of the covariance

matrix contains the variances σ

of the random values ε

, non diagonal elements

describe a linear relations between values ε

and ε

Along with the covariance matrix R a correlation matrix with the elements

√

is used often enough. The main diagonal of the correlation matrix contains units

and nondiagonal elements r

are the correlation coeﬃcients of the values ε

and

Let’s consider special cases of the covariance matrix R, which are very important

from the practical point of view.

1. The vector

ε has a property of a stationarity in the wide sense, i.e. the

values of a vector of the mathematical expectation and the variance are constant,

and the correlation matrix depends only on a diﬀerence of indexes i and i

, thus on

diagonals, parallel to the main diagonal, the identical values are placed

r =





1 r

. . . r

. . . . . . . . . . . . . . .

n−1

n−2

. . . 1





2. In a case of a noncorrelated random component the covariance matrix can be

written as

= σ

where δ

is the Kronecker delta:



1, if i = i

0, if i 6= i

At equal accuracy measurements

R = σ

where I is an identity matrix. In this case it is easy to calculate the inverse matrix

−1

Now the density of probabilities is possible to write as

p(εε) = (2πσ

)

−n/2

exp



−

2σ

(ε − ε

)



108 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

Fig. 3.7 The elements of the covariance matrix in the case the Markovian process (3.21) (σ = 1,

c = 1).

3. To consider the Markovian type of the correlation. In this case correlation of

random quantities ε

and ε

is described by the following function

= σ

exp{−c|i − i

|} (3.21)

(Fig. 3.7). Introducing the designation γ = exp(−c) we obtain the next representa-

tion for the matrix R:

R = σ







1 γ γ

. . . γ

γ 1 γ . . . γ

n−1

. . . . . . . . . . . . . . .

n−1

n−2

. . . 1







. (3.22)

the determinant of R can be written as

|R| = σ

(1 − γ

)

n−1

. (3.23)

An essential advantage of a matrix R is that it can be inverted irrespectively of

the quantity n, thus the inverse matrix looks like

−1

(1 − γ

)







1 −γ 0 . . . 0

−γ 1 + γ

−γ . . . 0

. . . . . . . . . . . . . . .

0 0 0 . . . 1







. (3.24)

The formula (3.20) for the density function of ε taking into account (3.23) and

(3.24) can be rewritten as

p(ε) = (2πσ

)

−n/2

(1 − γ

)

(n−1)/2

exp{−

2σ

(1 − γ

)

× [(1 + γ

)

− 2γ

i+1

− γ

(ε

+ ε

)]}.

The simplicity of the matrix inversion (3.22) allows to use the Markovian type of a

correlation for the approximate description of more complex correlations.

The practical interest, for example, for the model (3.10), represents the fol-

lowing variant of the assignment of the random component ε

: the mathematical

expectation is equal to zero and ﬁnite interval of the time correlation

hε

i, hε

i−j

i, j ≥ n

Models of measurement data 109

where h·i is an averaging operator. In this case for ε

ε the next representation is valid

= εε

j=1

i−j

where h

i = 0, hε

i−j

i = σ

(δ

is the Kronecker delta function). The ma-

trix D

can be diagonal as well as nondiagonal. Such description of the random

component can be helpful for the sesimogram processing.

Along with stationary or quasi-stationary components of a random variable we

shall consider the non-stationary random component using an example of the one-

dimensional model

= f

+ σ

)ε

where f

, ε

are independent and identically distributed random variables

with the mathematical expectation 0 and an unknown symmetric density function.

According to a priori receipt about the character of a stationarity choose a view of

a functional dependence of σ

). For example,

= σ(1 + |f

, σ

= σ exp(λf

), σ

= σ|f

= σ(1 + λf

), σ

= σ(1 + λf

)

1/2

where λ, σ are unknown parameters, which estimate together with θθ.

Let’s note, that the made above assumption about a normality of estimates in

practice is not always observed. The presence of sharp outliers in a noise realization

can give an essential deviation from the normal distribution, thus statistical proce-

dures basing on the moments of the ﬁrst and second orders, can lose the optimum

properties. Under this conditions it is expedient to make the assumption, that the

variance of noise is known only on average. Applying the maximum entropy princi-

ple, we shall discover a distribution, which at the accepted assumption ensures the

greatest indeterminacy of the system, i.e. it is necessary to ﬁnd density ˆp(ε), which

gives a maximum of an entropy,

= −

∞

−∞

ˆp(ε) ln ˆp(ε)dε, ˆp(ε) = arg max H

Let’s we have a normal distribution for a random component, but the standard

deviation is a random variable with the mathematical expectation σ

. In this case

a desired density function ˆp(ε) can be written as follows

ˆp(ε) =

√

2π

∞

exp



−

(ε − ε

)

2σ



p(σ)dσ =

∞

l(ε, σ)p(σ)dσ,

where ε

is the mathematical expectation of the random variable ε. The density

function of σ satisﬁes the conditions

∞

σp(σ)dσ = σ

, (3.25)

110 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

∞

p(σ)dσ = 1. (3.26)

For ﬁnding the density function ˆp(ε) it is necessary at ﬁrst to determine ˆp(σ).

The maximum entropy method, taking into consideration the constrains (3.25),

(3.26) is reduced to ﬁnding of a conditional extremum. For its ﬁnding, we shall take

an advantage of the Lagrange method. The functional subject to a maximization,

looks like

L(p(σ)) = −

∞

−∞







∞

l(ε, σ)p(σ)dσ





∞

l(ε, σ)p(σ)dσ











dε

+ λ





∞

p(σ)dσ − 1





+ λ





∞

σp(σ)dσ −σ





The necessary condition leads to the solution of the equation

∂L

∂p

= 0,

∞

−∞

l(ε, σ)





∞

l(ε, σ)p(σ)dσ





dε + 1 − λ

− λ

σ = 0. (3.27)

It is easy to test, that the solution of the equation (3.27) with conditions (3.25),

(3.26) is a density function

p(σ) = (2/λ

)σ exp{−σ

/λ

}, (3.28)

where λ = 2σ

√

π. Then

ˆp(ε) =

∞

l(ε, σ)p(σ)dσ =

2α

exp



−|ε − ε



the density function of the standard deviation σ is equal

p(σ) =

2σ

exp{−σ

/λ

The obtained function ˆp(ε) is the Laplace density function. “The Tails” of this

density function decrease more slowly, than “tails” of the normal density function,

i.e. the values of errors ε with the appreciable deviation from the mathematical

expectation ε

can appear with higher the probability. Therefore the assumption

about an error of the distribution of observations ε under the Laplace law is more

cautious in comparison with the assumption of the normal law, if the dispersion of

the noise is not accurately known or unstable. In a Fig. 3.8 the density functions

of the normal and the Laplace distributions are represented.

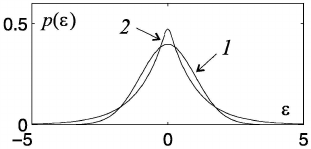
Models of measurement data 111

Fig. 3.8 Density functions: 1 — normal (ε

= 0, σ = 1); 2 — Laplace (ε

= 0, α = 1).

3.7 Model with Random Parameters

Along with the model (3.1), in which the vector of parameters is considered as

unknown, but nonrandom, the model with random parameters of signals can be

considered

u(x

, t

) =

µ=1

ϕ(t

− τ

µk

) + ε(x

, t

), (3.29)

where A

, τ

µk

are the random amplitude and moment of the arrival of the wave

with a number µ. Let’s consider the distribution of these arguments as normal with

the mathematical expectation 0 and variance σ

, σ

. The shape of the signal ϕ(t

)

is supposed the known determined function. A random component ε

has also a

normal distribution with the mathematical expectation 0 and covariance matrix R.

3.8 A Priori Information

Usually at conducting geophysical operations the interpreter has a priori informa-

tion, given by past geophysical explorations in this or adjoined regions, and also

given by the well logging on available deep wells. The engaging of this informa-

tion at creating algorithms of the interpretation and for making the automatized

system of the processing of geophysical data requires its formalization in the pure

mathematical shape.

In general case a priori information can be introduced by a system of algebraic

equations or inequalities:

Φ(

θ) = cc, (3.30)

≤ Φ

Φ(θ

θ) ≤ c

, (3.31)

where

θ is a vector of unknown parameters, Φ(

θ) is a given vector function.

For many practical applications it is possible to be conﬁned to a special case of

the formula (3.30), by the system of the linear equations:

Aθ = V , (3.32)

112 STATISTICAL METHODS OF GEOPHYSICAL DATA PROCESSING

where A and V are the given matrix and vector of absolute terms. Special case of

the formula (3.31) is the linear system of inequalities

≤ A

θ ≤ VV

, (3.33)

where

and V

are low and upper bounds of inequalities. As the problem of

an estimation, as a rule, consist in ﬁnding an extremum in the space of required

arguments, the account of a priori information leads to the problem of ﬁnding of a

conditional extremum, for ﬁnding of which one the method of Lagrange multipliers

is usually used.

If the model parameters are considered as random, the natural shape of the

representation of a priori information is the assignment of a priori probability dis-

tribution of required parameters. As such distributions the normal or uniform dis-

tributions are used more often. So, if for each of arguments, which one are assumed

independent, it is possible to specify a priori intervals of their variation, and the

arguments with the equal probability accept any values in these intervals, a priori

distribution of arguments will be uniform:

p(θθ) =







s=1

1/(θ

− θ

), θ

≤ θ

0, θ

(3.34)

where θ

and θ

are the low bound and upper bound of a priori variation of param-

eter θ

correspondingly.

At presence of great number of independent random factors aﬀecting arguments,

as a priori distribution the normal distribution is usually chosen, issuing from the

central limit theorem. If we shall assume, that the arguments are independent, then

a priori distribution will be written as

θ) =

s=1

(2πσ

)

−1/2

exp



−

s=1

(θ

− hθ



. (3.35)

Let’s assume, that the wave amplitude has the normal distribution with the mathe-

matical expectation hAi and the variance σ

. While the moment of the arrival time

and the apparent slowness γ have an uniform distribution with intervals [t

, t

]

and [γ

, γ

]. In this case the joint distribution function will be written as

p(A, t

, γ) =







[

√

2πσ

− t

)(γ

− γ

)]

−1

×if t

≤ t

×exp{−(A − hAi)

/2σ

}, and γ

≤ γ ≤ γ

0, for other t

, γ.

It is possible other alternatives of the assignment of a priori information, however

described here distributions are used most frequently in practice at constructing

algorithms of the interpretation of the seismic data.

The considered models of an experimental material do not encompass all variety

of practical situations. But they full enough illustrate conditions and opportunities,

connected with the statistical approach. At the solution of a concrete geophysical