Виссарионов В.И., Дерюгина Г.В., Кузнецова В.А., Малинин Н.К. Солнечная энергетика

Подождите немного. Документ загружается.

закономерные явления – суточные, годовые и многолетние циклы солнечной

активности, которые определяются обращением Земли вокруг Солнца и

собственной оси, а также межпланетными факторами. С другой стороны –

случайные изменения СИ, из-за стохастической природы процессов в

атмосфере (циркуляция потоков, облачность, аэрозоли, пыль и т.д.). Все это

требует использования при изучении СИ на Земле не только

детерминированных, но и вероятностных подходов. Особое значение здесь

приобретают средневзвешенные значения (или математические ожидания)

тех или иных показателей СИ. Особенно это полезно для ведения расчетов по

системным СЭУ, но также важно и для других случаев использования СЭУ в

разделах, связанных с финансово-экономическими расчетами по СЭУ.

Естественно, что здесь особое значение приобретает точность полученных

оценок и требующаяся для расчетов длина рядов наблюдений за СИ. В связи

со сказанным в таблице 2.2 приведены характерные ошибки в процентах для

разных временных расчетных интервалов по основным составляющим СИ в

бывшем СССР (приборные, микропогодные и микроклиматические

различия).

Из данных таблицы 2.2 следует, что с увеличением расчетного периода

значение погрешности по всем составляющим СИ существенно уменьшается.

Например, для Э

пр

при переходе от ∆t =1 сутки ∆t=1 мес и далее 1 год

погрешность снизилась с 40% до 12 % и далее до 3 %. Из сказанного следует,

что, очевидно, при переходе к ∆t =1 час ошибки в оценке потока СИ будут

еще большими. Наибольшие ошибки в таб 2.2. Характерны для Э

пр

, которая

наиболее необходима для всех видов гелиоэнергетических расчетов. Следует

заметить, что все данные, рассмотренные выше, относятся только к

горизонтальным ПП.

Погрешности Э

мес

Для наиболее представительных среднемесячных значений потока СИ

по имеющимся рядам наблюдений были определены аналитически их

ошибки в зависимости от длины ряда наблюдений, т.е. m

1-n

(2.11)

где

- среднеквадратичное отклонение СИ за ∆t=1 мес или 1 год; n –число

лет.

Таблица 2.2 Характерные ошибки в расчетах потока СИ за ∆t=1 сутки,

1 месяц и 1 году по 4-м сезонам года и год в целом

Составляющие

СИ

I IV VII X Год в

целом

∆t=1 мес и 1 год

∑

8 4 3 5

1,5÷2

пр

12 - 5 - 3

6 - 3 - 2

∆t=1 сутки

∑

15 9 8 12 -

пр

40 20 15 30 -

20 11 9 11 -

В целом для бывшего СССР имеем следующие основные ошибки в

∑

мес ,

год

мес

, Э

пр

мес

и Э

пр

год

, представленные в таблице 2.3. Из таблицы 2.3

следует, что погрешности в расчетах Э

пр

существенно превосходят

погрешности в расчетах Э

∑

как для месячного, так и годового расчетного

периода.

Таблица 2.3 Основные ошибки в расчете Э

мес

и Э

год

для суммарного и

прямого СИ

∑

мес

пр

мес

СИ

холодный

период

теплый

период

∑

год

холодный

период

теплый

период

пр

год

, % 3÷7 2÷5 1÷2 5÷20 4÷10 2÷5

В качестве иллюстрации в таблице 2.4 приведены данные по ошибкам

в процентах для расчета СИ за ∆t=1 мес и 1 год в зависимости от длины

периода наблюдений. Там же даются два вида ошибок: основная ошибка и

ошибка при доверительной вероятности 0,9 с учетом распределения

Стьюдента. Последняя ошибка (m

) определяется по формуле:

1-n

t σ

⋅

, (2.12)

где

квантиль распределения Стьюдента.

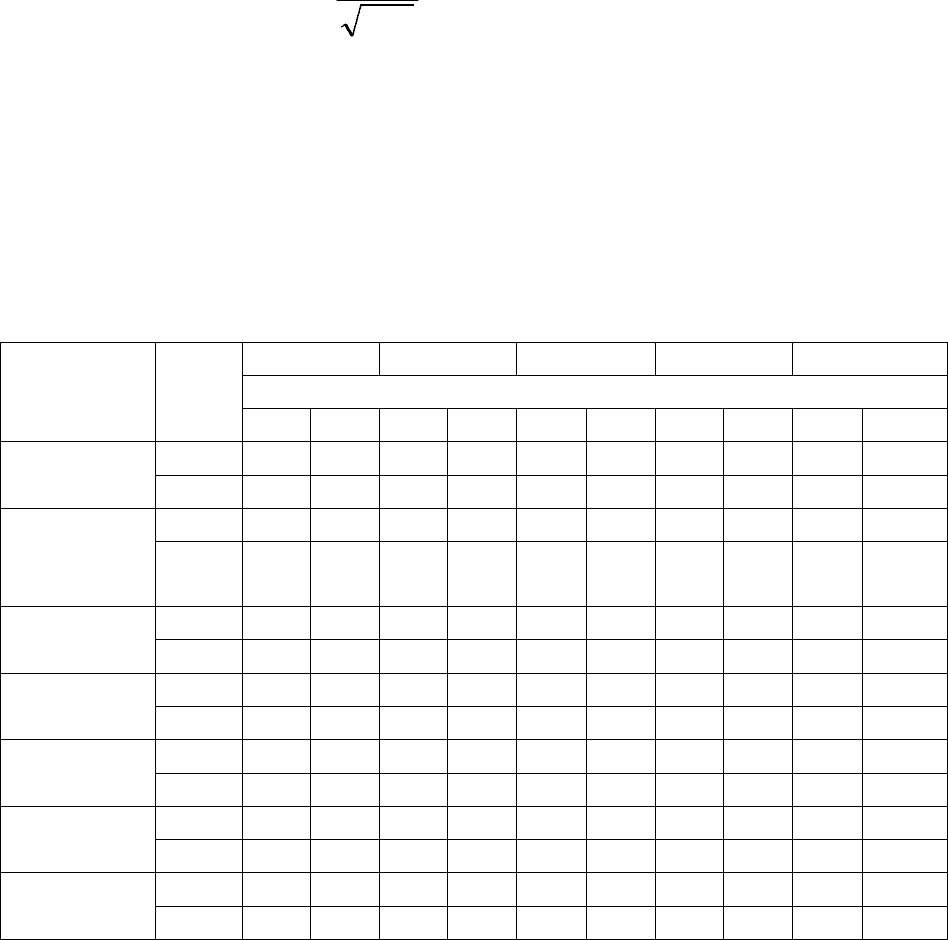
Таблица 2.4 Основные ошибки и ошибки при доверител вероятности

0,9 для расчетов потока СИ за ∆t=1 мес или 1 год в зависимости от длины

периода наблюдений

I IV VII X год

Число лет наблюдений

АМС

оши-

бка

15 30 15 30 15 30 15 30 15 30

а 3,3 2,3 1,5 1,3 2,4 1,6 2,3 1,8 1,2 0,8

г.Якутск

б 5,8 3,9 2,7 2,2 4,0 2,7 4,0 3,0 2,2 1,3

а 5,5 3,9 4,9 2,7 3,7 2,1 4,9 3,5 1,0 0,9 ГГО им.

А.И.Воей-

кова

б 9,6 6,6 8,5 4,5 6,5 3,6 8,5 5,9 1,7 1,5

а 2,9 1,5 2,1 1,6 3,7 2,1 4,0 2,9 0,9 0,8

Верхнее

Дуброво

б 5,0 2,5 3,6 2,8 6,5 3,6 7,0 4,9 1,6 1,3

а 2,3 1,5 2,6 1,5 1,8 1,6 2,6 1,8 0,7 0,7

Иркутск

б 4,1 2,0 4,5 2,6 3,2 2,7 4,5 3,1 1,2 1,3

а 5,1 3,2 4,1 2,4 1,4 0,8 2,1 1,4 0,8 0,5 Карадаг

б 9,0 5,5 7,1 4,0 2,5 1,4 3,6 2,4 1,4 0,8

а 4,0 2,4 4,1 2,7 2,2 1,6 4,0 2,6 1,5 1,0 Тбилиси

б 7,0 4,1 7,2 4,5 3,8 2,7 7,0 4,4 2,6 1,7

а 3,2 2,1 3,6 2,5 1,5 1,0 2,7 1,6 0,9 0,8

Ташкент

б 5,6 3,5 6,3 4,2 2,6 1,7 4,7 2,7 1,5 1,3

Примечание: а – основная ошибка; б- ошибка при доверительной вероятности 0,9.

С помощью (2.11) и (2.12) можно определить требуемое число лет

наблюдений (n) за СИ при заданной точности гелиоэнергетических расчетов,

определяемой видом рассматриваемой задачи. Если принять во внимание

погрешности исходных рядов в таблице 2.2, то при доверительной

вероятности 0,9 необходимая длина ряда наблюдений за СИ будет равна 30

годам, а при вероятности 0,68 – не более 15 лет.

Все только что рассмотренное выше по погрешностям и n

треб

относилось к месячному потоку СИ, что пригодно для расчетов параметров и

режимов системных СЭУ.

Для СЭУ, работающих на локальную сеть или на автономного

потребителя, требуются данные по СИ за ∆t не более 1 суток. Переход от Э

мес

к Э

сут

затрудняется в целом следующим обстоятельством. Если между

смежными значениями потоков СИ за j-ый и j+1 месяцы корреляционная

связь очень мала, то суточные значения потоков СИ за смежные сутки имеют

весьма тесную корреляционную связь. В связи с этим увеличиваются и

значения ошибок в расчете Э

сут

по сравнению с указанным в таблице 2.4. для

учета взаимосвязи Э

сутi

и Э

сут(i+1)

(т.е. представление их в виде простой цепи

Маркова) в выражение для расчета m

вводится дополнительный множитель,

в котором учитывается r

(о.е.) – коэффициент корреляции между смежными

значениями Э

сутi

и Э

сут(i+1)

,т.е.

⋅

−

⋅

− 1

σσ

. (2.13)

Наиболее часто встречающееся значение r

для АМС бывшего СССР

равно 0,25 ÷0,45. Соответственно

=1,29÷1,62. В качестве подтверждения

сказанного в таблице 2.5 приведены погрешности в процентах Э

∑

сут

для

разных регионов бывшего СССР.

Расчеты по рядам наблюдений за СИ для определения погрешности в

∑

сут

показали, что для 35 ÷ 40 летних рядов ошибка не превышает (1 ÷3)%

при доверительной вероятности в 0,9 и учете взаимосвязи Э

сутi

и Э

сут(i+1).

Для

10-летних рядов погрешность не превышает 10%, что не выходит за пределы

точности исходных рядов, приведенных в табл.2.2.

Это означает, что даже 10-летние ряды Э

∑

сут

дают надежные

результаты по средним значениям Э

∑

сут

для климатологических расчетов.

Ряды наблюдений за СИ при ∆t=1 час необходимы для расчетов параметров и

режимов СЭУ, работающих на локальную сеть и, особенно, - на автономного

потребителя. Очевидно, что Э

∑

часi

и Э

∑

часi+1

имеют еще большую

корреляционную связь между собой, чем суточные значения потока СИ.

Поправочный коэффициент

в (2.13) в связи с этим возрастает до 1,7, как

следствие этого возрастают и погрешности расчетов. В частности для

расчетов, выполненных по бывшим среднеазиатским республикам СССР

было выявлено, что ошибка в Э

∑

час

для времени полудня при

доверительной вероятности в 0,9 и учете корреляционной связи Э

∑

часi

∑

часi+1

составила: летом – 3%, другие сезоны года – (4÷5)%. Соответственно,

для Э

пр

час

: (5÷6)% и (8÷10)%. Для исходного ряда в 10 лет ошибки в Э

∑

час

увеличились до (6÷8)%, а Э

пр

час

- до 15%.

Для других часовых интервалов внутри Т

сс

каждых суток погрешности

в расчетах потока СИ увеличиваются по сравнению с полуденным часом.

Однако и здесь ряд наблюдений за СИ в 10 лет может считаться вполне

надежным для климатологических расчетов.

В целом для климатологических целей наиболее предпочтительным

является для оценки общего состояния прихода СИ за разные ∆t (1 час; 1

сутки; 1 месяц; 1 год) представление данных по потоку СИ в виде

иллюстраций разных значений прихода СИ на горизонтальную ПП, т.е.

час

(ϕ

,ψ

)=const, Э

пр

(ϕ

,ψ

)=const, Э

(ϕ

,ψ

)=const. То же самое касается и

изолиний Т

сс

факт

(ϕ

,ψ

)=const для разных ∆t (1 час; 1 сутки; 1 месяц; 1 год).

Подобная информация вполне пригодна и для предварительных этапов

проектирования параметров и режимов СЭУ, когда ставится цель оценки в

целом масштабов прихода СИ в рассматриваемой точке А (ϕ

,ψ

Таблица 2.5 Погрешности (%) в определении Э

∑

сут

с учетом

использования простой цепи Маркова при доверительной вероятности 0,9

для бывшего СССР

Регионы I IV VII X

Европейская часть бывшего СССР

≥60

7-10 5-6 4-6 7-10

<ϕ

<60

5-7 4-6 3-5 6-9

≤50

4-7 3-6 2-4 2-7

Западная Сибирь и Средняя Азия

≥60

6-8 3-4 3-5 6-9

<ϕ

<60

4-5 3-4 3-4 5-7

≤50

3-7 3-7 1-3 3-5

Восточная Сибирь

≥60

5-8 2-4 4-7 5-10

<ϕ

<60

3-6 3-5 3-5 4-7

Дальний Восток

≥60

5-7 3-5 4-7 8-10

<ϕ

<60

4-5 3-5 5-6 5-6

≤50

3-5 4-6 4-7 4-7

В качестве примера на рис.2.5÷2.10 представлены в графическом виде

изолинии Э

∑

(∆t=1 год)=const, Э

∑

(∆t=январь, июль)=const, Т

сс

факт

(∆t=1

год)=const и Т

сс

факт

(∆t= январь, июль)=const.

Наличие подобных топограмм, построенных для разных временных

периодов (например, за (50 - 60)-е годы XX века и за (80 - 90)-е годы того же

века) может дать весьма представительную информацию для

климатологических расчетов с точки зрения динамики изменения

интенсивности и потока прихода СИ на Землю. Последнее имеет огромное

значение и для чисто энергетических расчетов по проектированию и

обоснованию режимов СЭУ разного назначения.

В частности, информация, представленная на рис.2.5÷2.10 позволяет

сделать следующие общие выводы.

Для России годовой приход солнечной энергии на 1 м

горизонтальной

ПП находится в пределах от 800 до 1400 кВт⋅ч/м

(минимум – для ϕ

около

сев. широты (полуостров Таймыр); максимум в районе г.Владивостока). В

среднем около 1000 кВт⋅ч/м

по всей территории страны, что существенно

меньше максимальных значений прихода СИ на Земле (2200 кВт⋅ч/м

) и

соответствует среднеевропейским странам, где широко используется СИ в

целях энергетики. Например, Германия, находящаяся на широтах от 47,5

до

55,00 сев. широты, т.е. примерно на широтах от г.Ростов-на-Дону до

г.Москвы.

Для региона Восточной Сибири и Восточного побережья озера Байкал

следует выделить аномальную зону с повышенным значением годового

прихода СИ. В январе месячная норма прихода СИ снижается до 5 ÷45

кВт⋅ч/м

, а в июне достигает 150 ÷200 кВт⋅ч/м

для широт, указанных выше.

Продолжительность солнечного сияния за год на горизонтальной ПП

находится в пределах от до ч или в среднем около ч.

В январе Т

сс

факт

снижается, а в июне составляет ч.

Накопленная на сегодня информация по СИ на территории России

позволяет:

- выполнить климатические обобщения для изучения основных

закономерностей радиационного климата России и простанственно-

временной структуры радиационных характеристик;

- оценить природный или валовой потенциал солнечной энергетики в

России.

Обобщенные значения Э

∑

, Э

пр

, а также коэффициента прозрачности

атмосферы K

, как отношения Э

пр

к Э

∑

приведены ниже в таблице 2.6 для

Европейской и Азиатской части России (ЕЧР и АЧР).

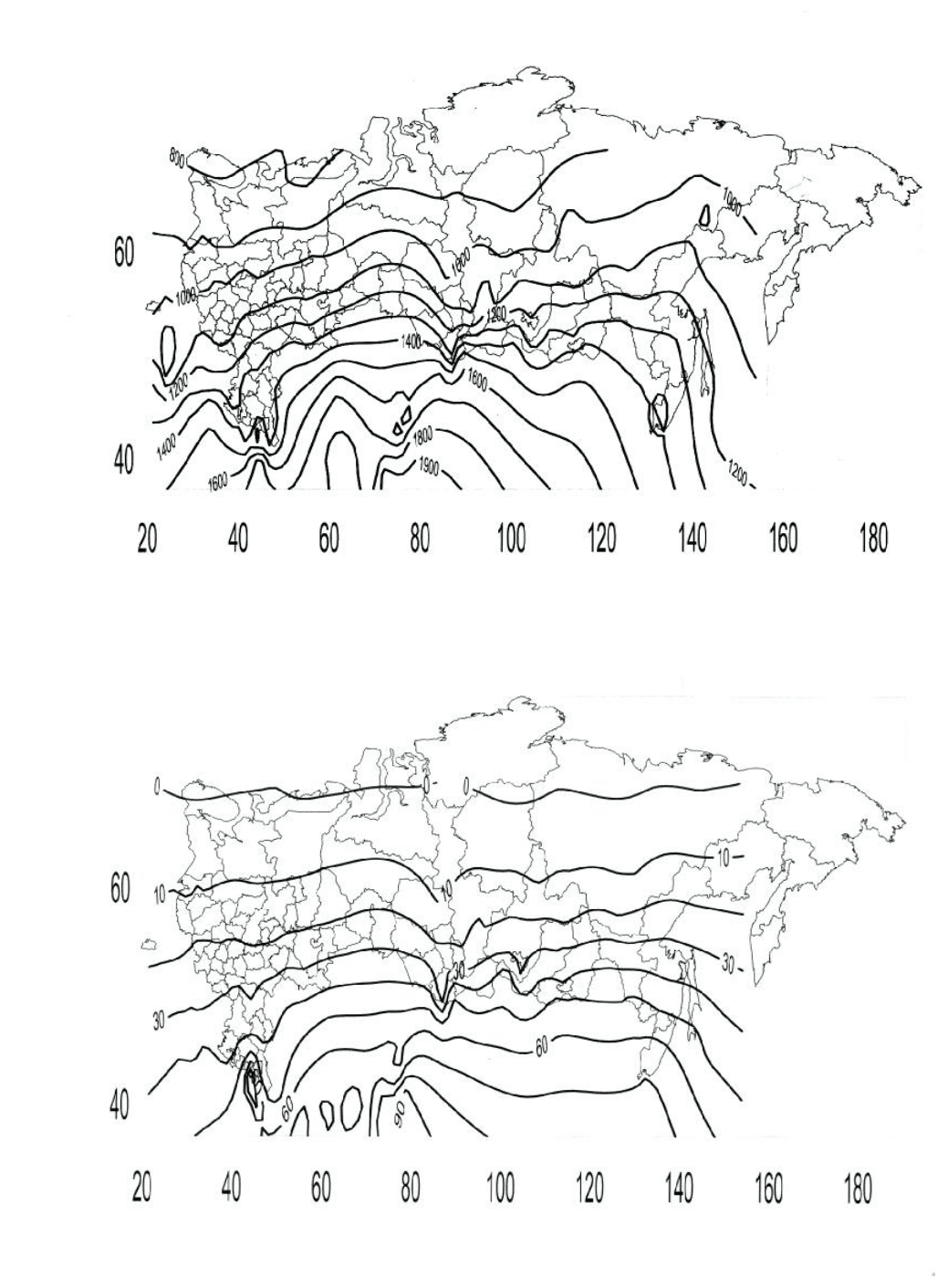
Рисунок 2.5 Среднемноголетние годовые значения Э

∑

для РФ

Рисунок 2.6 Среднемноголетние значения для января Э

∑

для РФ

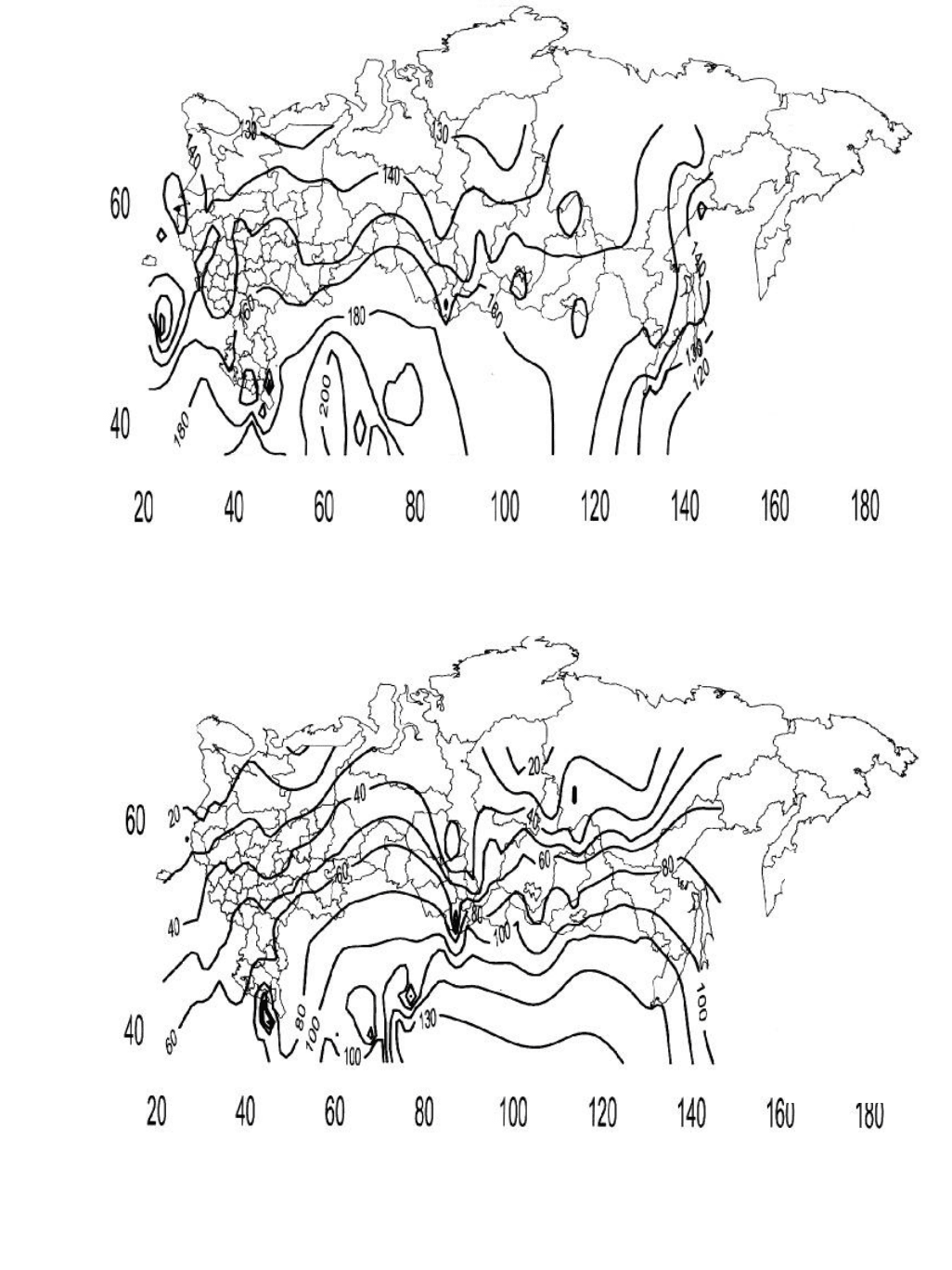
Рисунок 2.7 Среднемноголетние значения для июня Э

∑

для РФ

Рисунок 2.8 Среднемноголетние годовые значения Э

∑

при

для РФ

Рисунок 2.10 Среднемноголетние значения для июня Э

∑

при β

=ϕ

для РФ

Рисунок 2.9 Среднемноголетние значения для января Э

∑

при

для

РФ