Витяев Е.Е. Извлечение знаний из данных. Компьютерное познание. Модели когнитивных процессов (2006)
Подождите немного. Документ загружается.

81
Покажем, что в результате удаления условия η(A
0
/A
1
& ... &A
k
) = 1 из
определения вероятностного закона для детерминированного случая
(определение 15) мы ничего не потеряли из существа определения закона.
Вспомним, что именно свойство неупрощаемости позволило нам
сформулировать определение вероятностного закона в детерминирован-
ном случае. Посмотрим на результат предыдущей теоремы (теорема 7) с
точки зрения
неупрощаемости закона. В вероятностных терминах свойст-
во неупрощаемости закона звучит уже несколько иначе: для правила, ис-
тинного на M, для которого условная вероятность равна 1, неупрощае-
мость правила означает, что, если мы возьмем любое логически более
сильное его подправило, то его условная вероятность строго уменьшится и
станет строго меньше 1, т. е. вероятностный закон
на Exp в детерминиро-
ванном случае нельзя упростить, не уменьшив существенно его условную
вероятность. Поэтому два эквивалентных определения закона, сформули-
рованные в теореме могут быть переформулированы в терминах неупро-
щаемости закона, только одно из них для значения истинности, а другое
для условной вероятности. Из этой переформулировки видно, что для по-
нятия закона
важны не сама истинность или то, что условная вероятность
равна 1, а невозможность его упрощения с сохранением этих оценок (ис-
тинности, вероятности и т. д.). Это дает возможность дать более общее оп-
ределение закона для правил вида (1), охватывающее как детерминирован-
ный так и вероятностный случаи.
Определение 19. Законом является такое правило C вида (1), характе-
ризуемое некоторой оценкой, что его нельзя «упростить» (логически уси-
лить – теорема 4) не уменьшив существенно этой оценки.
Эквивалентность двух различных определений закона с точки зрения
данного определения закона для двух различных видов оценок – оценки
истинности и оценки условной вероятности, равной 1, доказана (теорема
7). При переходе от
вероятностного закона в детерминированном случае
(определение 15) к вероятностному закону (определение 17) мы заменили
оценку закона с условной вероятности равной 1 на просто оценку услов-
ной вероятности, оставаясь в рамках закона (определение 19).
Условная вероятность, используемая нами (теорема 7, определение 15,
определение 17) как оценка закона, интересна не только тем, что это веро-
ятность, но еще и
тем, что она является оценкой предсказательной силы
закона, являющейся наиболее важной характеристикой законов вообще.
Понятие закона всегда, прежде всего, связывается с его способностью
предсказывать, поэтому переход от характеристики закона в терминах ис-
тинности, принятой в философской логике и связанной с принципом фаль-
сифицируемости, к характеристике закона в терминах предсказания явля-
82
ется не просто уходом от старой парадигмы (включая принцип фальсифи-
цируемости), а переходом к более естественному определению закона.
Теорема 7 в этом случае означает, что для детерминированного случая,
который характеризует возможность предсказания в случае отсутствия
шумов, определения закона через истинность и условную вероятность
совпадают. Но если мы имеем стохастический случай, когда
правила не
истинны на M, определение закона через истинность теряет свой смысл, а
определение закона, основанное на условных вероятностях и предсказа-
нии, сохраняет свой смысл.
Понятие гипотезы, используемое в философской логике и связанное с
принципом фальсифицируемости, отличается от определения закона. По-
этому понятно, почему в литературе нет определения закона природы.
Следует подчеркнуть
, что определение закона природы (и на это опреде-
ление претендует наше определение) должно служить мостом между тео-
ретическим (идеальным) и эмпирическим уровнями рассмотрения.
Закон в
отличие от гипотез
идеален. Поэтому проверка и обнаружение закона ни-
как не могут быть связаны с принципом фальсифицируемости. В нашем
определении обнаружение закона связано с его (вероятностной) неупро-
щаемостью, которая тесно связана с такими присущими законам свойст-
вам как простота, логическая сила, максимальная общность (или фальси-
фицируемость) и минимальность числа параметров.
Множество вероятностных законов
шире множества законов (см.
предложение 3), поэтому, обнаруживая вероятностные законы, мы будем
обнаруживать как аксиомы теории Σ так и просто вероятностные законы.
Чтобы выделить среди вероятностных законов аксиомы из Σ есть два пути.
Первый путь, рассматриваемый в следующем параграфе, состоит в нахож-
дении условий, при которых множества вероятностных и (детерминиро-
ванных) законов
совпадают, и второй путь, рассматриваемый в следующей
главе, состоит в нахождении непротиворечивых подмножеств вероятност-
ных законов.
§ 26. Тестирование систем аксиом в условиях шумов
Процесс получения результатов эксперимента (см. определение 16)
можно разделить на два этапа: получение результатов эксперимента в
«чистом» виде, как «фрагмента» некоторой эмпирической системы, а за-
тем получение результатов реального эксперимента «добавлением» шу-
мов. Выделить эти два этапа можно, введя две вероятностных меры для
значений экспериментов: вероятностную меру в детерминированном и
стохастическом
случаях. Первая их них D
µ
будет удовлетворять дополни-
тельному требованию 2 (определение 16) для вероятностей в детермини-
рованном случае, а вторая S
µ
будет вероятностной мерой в общем случае.
83
Введение двух вероятностных мер позволит нам ввести вероятностную
модель шумов. Вернемся к определению эксперимента (определение 16)
Exp(s) = F〈〈a
1
, ..., a
m
〉, I(M)I(X(Σ))s〉.
Стохастический эксперимент Exp(s) получается в два этапа: сначала
получается результат детерминированного эксперимента в соответствии с
вероятностной мерой D
µ
, а затем применяется случайное преобразование
F, отражающее влияние на результаты детерминированного эксперимента
шумов, ошибок, неточности приборов и т. д. в соответствии с вероятност-
ной мерой S
µ
. Приведем соответствующие определения.
Определим переход от значений детерминированного эксперимента,
представленного некоторыми наборами в двоичном кубе E, к значению
стохастического эксперимента как действие случайной функции F : E → E.
Отображение F есть некоторое случайное взаимнооднозначное отображе-
ние. Вероятностные характеристики этого отображения и соответственно
модель шумов задаются соотношением двух вероятностей D
µ
и S
µ
. При
этом вероятность S
µ
– есть вероятность реальных экспериментов, а D
µ
–
вероятность гипотетического «идеального» эксперимента на эмпирической
системе.
Устойчивость понятия вероятностной закономерности относительно
некоторого типа шумов означает, что если некоторое множество правил
{C
i
} является множеством вероятностных законов в детерминированном
случае, то то же самое множество правил будет множеством вероятност-
ных законов и в стохастическом случае.
Эта формулировка ставит следующую проблему: определить какие ве-
роятности и модели шумов сохраняют множество вероятностных законов.
Определение 20. Назовем сохраняющими моделями шумов такие пары
вероятностей S
µ
, D
µ
, для которых множество вероятностных законов LP
для вероятности S
µ
и множество законов L для вероятности D
µ
совпадают.
Если мы ограничим себя рассмотрением только сохраняющих моделей
шумов, то задача 6 решается так же, как задача 7.
Поэтому данная работа ставит проблему: определить множество сохра-
няющих моделей шумов. Но как определить является ли модель шумов со-
храняющей или нет. Это можно сделать либо аналитически, либо машин-
ным моделированием. Пример аналитического
доказательства приведен в
следующем параграфе.
§ 27. Сохраняющий двоичный шум
Предположим, что у нас есть эксперимент Exp(s) = 〈〈a
1
, ..., a
m
〉,
I(M)I(X(Σ))s〉 и вероятность для детерминированного случая D
µ
. Опреде-
лим шумы, задающие случайное преобразование F : E → E. Предположим,
84
что каждое атомарное высказывание, значение которого получается в экс-
перименте, подвергается воздействию независимой и одинаково распреде-
ленной двузначной случайной величины Λ, принимающей значение 1 с ве-
роятностью λ > 0.5 и 0 с вероятностью 1-λ. Если значения эксперимента
представить как двоичный вектор 〈1, 1, 0, ..., 0, 1〉, где 1 – истина, а
0 – ложь, то преобразование F : E → E примет вид:
〈
1, 1, 0, ..., 0,1〉 ⇒ 〈λ
1
1, λ
2
1, λ
3
0, ..., λ
n-1
0, λ
n
1〉,
где λ
1
, λ
2
, ..., λ
n
– различные независимые случайные величины с распре-
делением Λ. Эксперимент с преобразованными значениями атомарных вы-
сказываний обозначим через FExp(s). Пусть S
µ
– вероятность (определение
16) для случайно преобразованного эксперимента.
Теорема 8. Множества вероятностных законов для эксперимента Exp(s)
с вероятностью D
µ
и эксперимента FExp(s) с вероятностью S
µ
равны.
Доказательство. Нужно доказать, что правило C = (A
1
& ... &A
k
⇒ A
0
)
является вероятностным законом для эксперимента Exp(s) тогда и только
тогда, когда оно является вероятностным законом для эксперимента
FExp(s). В стохастическом эксперименте FExp(s) правило λ*C примет вид
(λ
1
*A
1
& ... &λ
k
*A
k
⇒ λ
0
*A
0
), где λ
1
*, ..., λ
k
*, λ
0
* – случайные величины
вида λ
1
λ
2
, ..., λ
n
, если литера A
1
, ..., A
k
, A
0
не содержит отрицания, или
случайные величины вида 1 - λ
1
, 1 - λ
2
, ..., 1 - λ
n
, если литера содержит от-
рицание.
Надо доказать, что правила C = (A
1
& ... &A
k
⇒ A
0
) и
λ*C = (λ
1
*A
1
& ... &λ
k
*A
k
⇒ λ
0
*A
0
) одновременно либо являются, либо не
являются вероятностными законами. Докажем это последовательностью
эквивалентных преобразований. Пусть правило λ*C является вероятност-
ным законом. Тогда
η(λ
0
*A
0
/ λ
1
*A
1
& ... & λ
k
*A
k
) > η(λ
0
*A
0
/ λ
2
*A
2
& ... & λ
k
*A
k
), (22)
для подправила вида 2 (теорема 4) (λ
2
*A
2
& ... &λ
k
*A
k
⇒ λ
0
*A
0
).
Распишем это неравенство:
η(λ
0
*A
0
/ λ
1
*A
1
& ... & λ
k
*A
k
) =
η(λ
0
*A
0
&λ
1
*A
1
& ... & λ
k
*A
k
) / η(λ
1
*A
1
& ... & λ
k
*A
k
) >
η(λ
0
*A
0
/ λ
2
*A
2
& ... & λ
k
*A
k
) =
η(λ
0
*A
0
&λ
2
*A
2
& ... & λ
k
*A
k
) / η(λ
2
*A
2
& ... & λ
k
*A
k
).
Рассматривая значения литер A
0
, A
1
, ..., A
k
, как точку в двоичном кубе,
мы можем заменить операцию конъюнкции на умножение. Тогда получим
следующее эквивалентное неравенство:
η(λ
0
*A
0
• λ
1
*A
1
•...• λ
k
*A
k
) / η(λ
1
*A
1
•...• λ
k
*A
k
) >
η(λ
0
*A
0
• λ
2
*A
2
•...• λ
k
*A
k
) / η(λ
2
*A
2
•...• λ
k
*A
k
).
85
Это неравенство легко преобразуется эквивалентным образом в силу
независимости случайных величин λ как между собой так и относительно
литер A
1
, ..., A
k
, A
0
:
η(λ
0
*A
0
• λ
1
*A
1
•...• λ
k
*A
k
) / η(λ
1
*A
1
•...• λ
k
*A
k
) =
η(λ
0
* • λ
1
* •…• λ
k
* • A
0
• A
1
•…• A
k
) / η(λ
1
* •…• λ
k
* • A
1
•… •A
k
) >
η(λ
0
*A
0
• λ
2
*A
2
•...• λ
k
*A
k
) / η(λ
2
*A
2
•...• λ
k
*A
k
) =
η(λ
0
* • λ
2
* •…• λ
k
* • A
0
• A
2
•…• A
k
) / η(λ
2
* •…• λ
k
* • A
2
•…• A
k
).
Если два события A, B независимы, то η(A&B) = η(A)η(B). Так как опе-
рация • является конъюнкцией, то η(A • B) = η(A)η(B). Отсюда получаем
следующее эквивалентное преобразование неравенства:
λ
0
* • λ
1
* •…• λ
k
* η(A
0
• A
1
•…• A
k
) / λ
1
* •…• λ
k
* η(A
1
•…• A
k
) >
λ
0
* • λ
2
* •…• λ
k
* η(A
0
• A
2
•…• A
k
) / λ
2
* •…• λ
k
* η(A
2
•…• A
k
) ⇔
η(A
0
• A
1
•…• A
k
) / η(A
1
•…• A
k
) > η(A
0
• A
2
•…• A
k
) / η(A
2
•…• A
k
)
Но последнее неравенство и есть то, что нам требуется доказать, а
именно вероятностное неравенство, аналогичное неравенству (22), но
только относительно правила C, а не правила λ*C. Так как последнее не-
равенство было получено эквивалентными преобразованиями, то обратное
так же верно, т. е. если неравенство (22) выполнено для правила C, то оно
будет выполнено и
для правила λ*C. Справедливость аналогичного нера-
венства относительно других подправил вида 2 (теорема 4) доказывается
аналогично. Таким образом справедливость теоремы относительно под-
правил вида 2 доказана.
Для завершения доказательства теоремы необходимо доказать анало-
гичное неравенство для подправил вида 1 (теорема 4).
Рассмотрим неравенство
η(λ
0
*A
0
/λ
1
*A
1
& ... & λ
k
*A
k
) > η(¬λ
1
*A
1
/ λ
2
*A
2
& ... & λ
k
*A
k
)
Распишем его аналогичным образом. Отрицание ¬λ
1
*A
1
равно (1-
λ
1
*)A
1
. Но поскольку сама случайная функция λ
1
* есть либо λ
1
, либо 1-λ
1
в
зависимости от наличия либо отсутствия отрицания у атома A
1
, то обозна-
чение случайной величины ¬λ
1
* можно оставить тем же самым, а именно
λ
1
*. Поэтому мы получим неравенства
η(λ
0
*A
0
/ λ
1
*A
1
& ... & λ
k
*A
k
) =
η(λ
0
*A
0
&λ
1
*A
1
& ... & λ
k
*A
k
) / η(λ
1
*A
1
& ... & λ
k
*A
k
) >
η(λ
1
*A
1
/ λ
2
*A
2
& ... & λ
k
*A
k
) =
η(λ
1
*A
1
&λ
2
*A
2
& ... & λ
k
*A
k
) / η(λ
2
*A
2
& ... & λ
k
*A
k
).
Заменим операцию конъюнкции на операцию умножения.
η(λ
0
*A
0
•λ
1
*A
1
•...•λ
k
*A
k
) / η(λ
1
*A
1
•...•λ
k
*A
k
) >
η(λ
1
*A
1
•λ
2
*A
2
•...•λ
k
*A
k
) / η(λ
2
*A
2
•...•λ
k
*A
k
).
86
Проведем серию эквивалентных преобразований.
η(λ
0
*A
0
• λ
1
*A
1
•...• λ
k
*A
k
) / η(λ
1
*A
1
•...• λ
k
*A
k
) =
η(λ
0
* • λ
1
* •…• λ
k
* • A
0
• A
1
•…• A
k
) / η(λ
1
* •…• λ
k
* • A
1
•…• A
k
) >
η(λ
1
*A
1
• λ
2
*A
2
•...• λ
k
*A
k
) / η(λ
2
*A
2
•...• λ
k
*A
k
) =
η(λ
1
* • λ
2
* •…• λ
k
* • A
1
• A
2
•…• A
k
) / η(λ
2
* •…• λ
k
* • A
2
•…• A
k
).
Отсюда получаем следующие эквивалентные преобразования.
λ
0
* • λ
1
* •…• λ
k
* η(A
0
• A
1
•…• A
k
) / λ
1
* •…• λ
k
* η(A
1
•…• A
k
)>
λ
1
* • λ
2
* •…• λ
k
* η(A
1
• A
2
•…• A
k
) / λ
2
* •…• λ
k
* η(A
2
•…• A
k
) ⇔
λ
0
* η(A
0
• A
1
•…• A
k
) / η(A
1
•…• A
k
) >
λ
1
*η(A
0
• A
2
•…• A
k
) / η(A
2
•…•A
k
)
Так как λ
0
* = λ
1
* = λ, то мы получаем требуемое неравенство, так как
последнее неравенство и есть то, что нам требуется доказать. Аналогичное
доказательство проводится для остальных подправил вида 1 (теорема 4).
87
ГЛАВА 3. ЛОГИЧЕСКИЙ ПУТЬ ПОЗНАНИЯ.
ПРОБЛЕМА ПРЕДСКАЗАНИЯ.
§ 28. Знание и познание
В предыдущей главе был рассмотрен процесс познания, основанный на
теории измерений. Он состоял в разработке метода обнаружения эмпири-
ческой аксиоматической теории предметной области, включающей систе-
мы аксиом, представленной некоторой эмпирической системой.
Рассмотрим более общую задачу.
Задача 8. Обнаружить эмпирическую аксиоматическую теорию, вклю-
чающую не только теорию эмпирической системы вместе с системами ак-
сиом, но и знания.
Знания – это высказывания, имеющие некоторую степень вероятности,
нечеткости, достоверности и т. д.
Рассмотрение знаний сталкивается со следующими принципиальными
и нерешенными проблемами:
1)
знания логически противоречивы и не образуют теорию;
2)
предсказание для знаний плохо определено – вероятностные оцен-
ки знаний резко падают в процессе логического вывода;
3)
предсказания, получаемые из знаний, статистически двусмысленны.
Эти проблемы известны и обсуждаются, например, в широко цитируе-
мой работе L. De Raedt and K. Kersting. «Probabilistic logic learning» [141].
В ней говорится, что «одними из центральных вопросов методов извлече-
ния знаний и искусственного интеллекта является вероятностное логиче-
ское обучение, т. е. интеграция реляционных или логических представле-
ний, вероятностного вывода и обучения».
Проблемы
1–3 являются следствием более глубокой проблемы:
4)
в настоящее время не существует адекватного синтеза логики и ве-
роятности.
Этой проблеме в 2002 г. был посвящен workshop «
Combining Probability
and Logic”
(King's College London 4th–6th November 2002). В аннотации к
workshop говорится: «Artificial intelligence is one key discipline in which
probability theory competes with other logics for application. It is becoming vi-
tally important to evaluate and integrate systems that are based on very different
approaches to reasoning, and there is strong demand for theoretical understand-
ing of the relationships between these approaches».
Во введении к спецвыпуску «Journal of Applied Logic» 1 (2003), Special
issue on Combining Probability and Logic, посвященному этому workshop,
Jon Williamson, Dov Gabbay писали: «One approach is to argue that
probabil-
ity is logic, which requires showing that probability is a determinate relation be-
88
tween statements. Kyburg, Howson and Paris and Vencovská appeal to the con-
cepts of frequency, consistency and entropy respectively to determine this rela-
tion. Alternatively one can explore other formalisms which
interface between
probability and logic: argumentation in the case of Fox and Kohlas; default rea-
soning in the case of Bourne and Weydert».
Однако настоящего синтеза логики и вероятности в этих работах не
сделано.
Нам удалось разрешить проблемы 1–4 и осуществить синтез логики и
вероятности для понятия предсказания [154; 157–158]. Предсказание явля-
ется одним из важнейших понятий в науке, однако до сих пор адекватного,
с нашей точки зрения, определения этого понятия не существует. Мы по-
кажем
, что это связано с нерешенностью проблемы 4. Решение проблемы 4
как и других проблем связано с радикальным изменением парадигмы в ло-
гике: предсказание нельзя вывести, его можно только вычислить. Такой
процесс вычисления нами разработан на основе семантического вероятно-
стного вывода, который следует идее семантического подхода к програм-
мированию выдвинутого Ю. Л. Ершовым,
С. С. Гончаровым и Д. И. Сви-
риденко. Идея семантического программирования состоит в том, чтобы
процесс вычисления рассматривать как проверку истинности утверждений
(включая возможное использование логического вывода) на некоторой
модели (моделью могут быть данные, представленные некоторой много-
сортной системой; некоторая специальная модель теории или абстрактного
типа данных и т. д.).
При таком взгляде на процесс вычисления, процедуру
логического вывода можно обобщить, рассматривая более разнообразные
взаимоотношения высказываний и модели – рассмотреть процесс вычис-
ления как, например, определение наиболее вероятных, подтвержденных
или нечетких высказываний на модели. Такой обобщенный вывод будем
называть семантическим.
В настоящее время определение понятия предсказания для индуктив-
ных теорий, содержащих знания
, осуществляется Индуктивно-
статистическим I–S (Inductive–Statistical) выводом. Гемпелем было заме-
чено, что предсказания получаемые
I–S-выводом статистически двусмыс-
ленны. Что бы избежать такой двусмысленности он ввел для законов, ис-
пользуемых в I–S-выводе, требование максимальной специфичности RMS
(
Requirement of Maximum Specificity). Он не дал формального определения
этому требованию, но дал достаточно четкую формулировку. Различные
формализации этой формулировки показали, что они также не решают
проблемы статистической двусмысленности. Из-за этой проблемы счита-
ется, что предсказание для индуктивных теорий не поддается адекватной
формализации.
В этой главе мы рассмотрим проблему формализации понятия предска-

89
зания для индуктивных теорий. Мы введем своё определение множества
всех максимально специфических правил MSR и докажем, что, во-первых,
оно непротиворечиво, а во-вторых, для него не возникает проблемы стати-
стической двусмысленности. Тем самым такие правила могут использо-
ваться в I–S-выводе без противоречий. Мы определим семантический ве-
роятностный вывод, который позволяет
вывести все четыре множества за-
конов L, LP и MSR.
§ 29. Индуктивно-статистический вывод
Индуктивно-статистический вывод Гемпеля по выводу некоторого
факта G имеет вид:
L
1
, …, L
m
C
1
, …, C
n
G
[r]
Он удовлетворяет следующим условиям:
i) L
1
, …, L
m
, C
1
, …, C
n
⇒ G;
ii) множество L
1
, …, L
m
, C
1
, …, C
n
непротиворечиво;
iii) L
1
, …, L
m
⊬G, C
1
, …, C
n
⊬G;
iv) множество L
1
, …, L
m
содержит статистические законы. Множество
фактов C
1
, …, C
n
не имеет кванторов;
v) RMS: все законы L
1
, …, L
m
максимально специфичны.
По Гемпелю [111], требование максимальной специфичности RMS
(Requirement of Maximal Specificity) определяется следующим образом.
I–S-вывод вида:
p(G;F) = r
F(
a)
G(a)
[r]
является приемлемым I–S-предсказанием при состоянии знания K, если
следующее требование RMS выполнено. Для каждого класса H, для кото-
рого оба следующих высказывания принадлежат K:
∀x(H(x) ⇒ F(x)),
H(
a),
(23)
Существует статистический закон p(G; H) = r’ в K такой, что r = r’. Ос-
новная идея RMS состоит в том, что если F и H оба содержат объект
a, и H
является подмножеством F, то H обладает более специфической информа-
цией об объекте
a чем F и следовательно закон p(G; H) должен предпочи-
таться закону p(G; F).
90
§ 30. Семантический вероятностный вывод.
Определение 21
. Под семантическим вероятностным выводом (СВВ)
некоторого сильнейшего вероятностного закона (СВЗ, см. определение 18)
мы понимаем такую последовательность вероятностных законов C
1
⊏ C
2
⊏ ... ⊏ C
n
, что
C
1
, C
2
, ..., C
n
∈ LP, C
i
=
ii
1ki
(A &...& A G)⇒
, i = 1, 2, ..., n, n ≥ 1,
правило C
i
является подправилом правила C
i+1
,
η(C
i+1
) > η(C
i
), i = 1, 2, ..., n-1 ,
C
n
– СВЗ-правило.
(24)
Предложение 4
. Любой вероятностный закон принадлежит некоторо-
му СВВ-выводу.
Предложение 5. Для любого СВЗ-закона существует СВВ-вывод этого
правила.
Следствие 3. Для любого закона из L существует СВВ-вывод этого за-
кона.
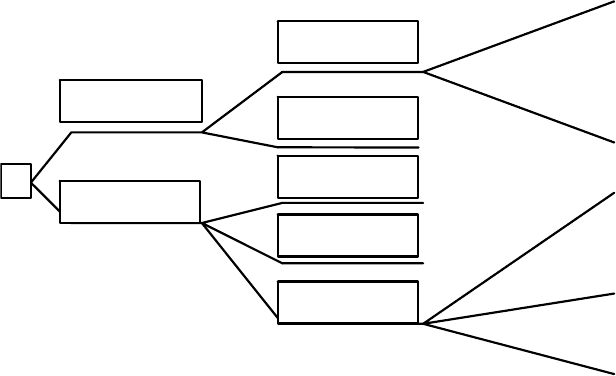
Рассмотрим множество всех СВВ-выводов некоторого факта G. Это
множество можно представить как семантическое вероятностное Дерево
выводов (СВДВ-дерево) факта G (рис 7).
Определение 22. Максимально специфическим законом вывода факта
G ( МСЗ(G) ) мы определим сильнейший вероятностный закон СВДВ-
дерева вывода факта G, имеющий максимальное значение условной веро-
G
⇐ A
1
1
&...&A
1
k1
&
⇐ A
2
1
&...& A
2
k2
&
A
7
k2+1
&...&A
7
k7
&
A
6
k2+1
&...&A
6
k6
&
A
5
k2+1
&...&A
5
k5
&
A
4
k1+1
&...&A
4
k4
&
A
3
k1+1
&...&A
3
k3
&
Рис 7.
