Wai-Fah Chen.The Civil Engineering Handbook

Подождите немного. Документ загружается.

29-30 The Civil Engineering Handbook, Second Edition

TA BLE 29.7 Physical Properties of Common Gases at Standard Sea-level Atmosphere and 68°F in English Units

Liquid

Chemical

Formula

Molecular

We ig ht

Speciﬁc

We ig ht,

lb/ft

Viscosity

m ¥ 10

lb·s/ft

Gas Constant

ft·lb/(slug·°R)

[= ft

/(s

·°R)]

Speciﬁc Heat,

ft·lb/(slug·°R)

[= ft

/(s

·°R)]

Speciﬁc

Heat

Ratio

k = c

Air 29.0 0.0753 3.76 1715 6000 4285 1.40

Carbon dioxide CO

44.0 0.114 3.10 1123 5132 4009 1.28

Carbon monoxide CO 28.0 0.0726 3.80 1778 6218 4440 1.40

Helium He 4.00 0.0104 4.11 12,420 31,230 18,810 1.66

Hydrogen H

2.02 0.00522 1.89 24,680 86,390 61,710 1.40

Methane CH

16.0 0.0416 2.80 3100 13,400 10,300 1.30

Nitrogen N

28.0 0.0728 3.68 1773 6210 4437 1.40

Oxygen O

32.0 0.0830 4.18 1554 5437 3883 1.40

Water v a p or H

O 18.0 0.0467 2.12 2760 11,110 8350 1.33

From Daugherty, R.L., Franzini, J.B., and Finnemore, E.J. (1985) Fluid Mechanics with Engineering Applications, 8th ed.,

McGraw-Hill, New York. With permission.

Fundamentals of Hydraulics 29-31

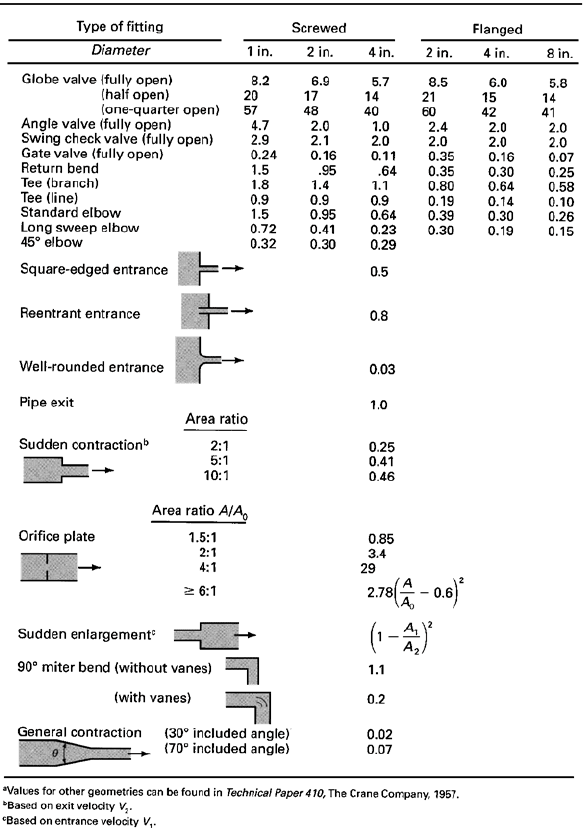
TA BLE 29.8 Nominal Minor Loss Coefﬁcients K

(turbulent ﬂow)

Adapted from Potter, M.C. and Wiggert, D.C. (1997). Mechanics of Fluids, 2nd ed., Prentice-Hall,

Englewood Cliffs, NJ.

29-32 The Civil Engineering Handbook, Second Edition

References

Bos, M.G. (ed.,) (1989) Discharge Measurement Structures, 3rd ed., publication 20, International Institute

Land Reclamation and Improvement, Wageningen, The Netherlands.

Miller, R.W. (1989) Flow Measurement Engineering, 2nd ed., McGraw-Hill, New York.

Sharpe, J.J. (1981) Hydraulic Modelling, Butterworths, London.

Yalin, M.S. (1971) Theory of Hydraulic Models, MacMillan, London.

Further Information

Most of the topics treated are discussed in greater detail in standard elementary texts on ﬂuid mechanics

or hydraulics, including:

Crowe, C.T., Roberson, J.A., and Elger, D.F. (2000) Engineering Fluid Mechanics, 7th ed., John Wiley &

Sons, New York.

Daugherty, R.L., Franzini, J.B., and Finnemore, E.J. (1985) Fluid Mechanics with Engineering Applications,

8th ed., McGraw-Hill, New York.

Fox, R.W. and McDonald, A.T. (1998) Introduction to Fluid Mechanics, 5th ed., John Wiley & Sons, New

Yo r k .

Gray, D.D. (2000) A First Course in Fluid Mechanics for Civil Engineers, Wa ter Resources Publications.

Potter, M.C. and Wiggert, D.C. (1997) Mechanics of Fluids, 2nd ed., Prentice-Hall, Englewood Cliffs, NJ.

Open Channel

Hydraulics

30.1 Deﬁnitions and Principles

Classiﬁcation of Flows • Flow Regimes

30.2 Balance and Conservation Principles

Conservation of Mass • Conservation of Momentum •

Piezometric Head • Boundary Shear • Total Thrust and Speciﬁc

Force • Balance of Mechanical Energy • Speciﬁc Energy •

Hydraulic Jump

30.3 Uniform Flow

30.4 Composite Cross-Sections

30.5 Gradually Varied Flow

30.6 Water Surface Proﬁle Analysis

The Mild Slope Proﬁles • The Steep Slope Proﬁles • The Critical

Slope Proﬁles • The Horizontal Slope Proﬁles • The Adverse

Slope Proﬁles

30.7 Qualitative Solution of Flow Proﬁles

Phase I — Determination of Critical Depths and Normal

Depths • Phase II — Virtual Control Section (VCS)

Determination • Phase III — Proﬁle Sketching

30.8 Methods of Calculation of Flow Proﬁles

30.9 Unsteady Flows

30.10 Software

Open channel hydraulics, a subject of great importance to civil engineers, deals with ﬂows having a free

surface in channels constructed for water supply, irrigation, drainage, and hydroelectric power generation;

in sewers, culverts, and tunnels ﬂowing partially full; and in natural streams and rivers. Open channel

hydraulics includes steady ﬂows that are unchanging in time, varied ﬂows that have changes in depth and

velocity along the channel, and transient ﬂows that are time dependent. This chapter deals only with rigid-

boundary channels without sediment deposition or erosion. In addition, this chapter assumes that wind

and surface tension stresses exerted on the free surface are negligible, and that velocities are low enough

that air is not entrained. The emphasis is on the one-dimensional treatment of uniform and nonuniform

ﬂows which are common in civil engineering practice. Design aspects of structures involving free surface

ﬂows are discussed in Chapter 35. Sediment transport in open channels is covered in Chapter 33.

30.1 Deﬁnitions and Principles

Open channel ﬂow

is the ﬂow of a single phase liquid with a free surface in a gravitational ﬁeld when the

effects of surface tension and of the overlying gas can be neglected. Because laminar open channel ﬂows

Aldo Giorgini

(deceased)

Donald D. Gray

West Virginia University

-2

The Civil Engineering Handbook, Second Edition

are seldom encountered in civil engineering practice, only turbulent ﬂows will be considered in this

chapter. The analysis of open channel ﬂows is largely based on the approximation that the mean stream-

lines are nearly parallel. As shown below, this implies that the piezometric head is nearly constant on

planes normal to the ﬂow, and allows a one-dimensional analysis. Regions of nonparallel streamlines are

considered by using control volume arguments. In some cases, these assumptions are inadequate, and a

much more complicated two- or three-dimensional analysis must be used.

For any given cross section, the following terminology and notation are used:

•The region of the cross section occupied by the liquid is called the

ﬂow area

•The part of the cross section perimeter which is below the water surface is called the

wetted

perimeter

•The length of the free surface is called the

top width

. This is normally assumed to be horizontal.

•The hydraulic depth is

•The hydraulic radius is

•The

water surface elevation, h

, is the vertical distance of the free surface above a reference elevation

or datum. In Fig. 30.1,

is the water surface elevation at cross section 2.

•The

invert

is the lowest point of the cross section.

•The vertical distance to the free surface from the lowest point of the cross section is called the

depth of ﬂow,

, or

depth

. Referring to Fig. 30.1,

is the depth corresponding to the invert at point A.

•The perpendicular distance from the invert to the free surface is called the

thickness of the stream

. Referring to Fig. 30.1,

is the thickness of the stream at cross section 1. If the free surface is

nearly parallel to the bottom of the channel,

y cos

, where

is the angle between the bottom

of the channel and the horizontal. For the small slopes normally encountered in rivers and canals



. The pressure head on the channel bottom is

y cos

d cos

For

< 5° the error in

approximating the pressure head by

is less than 1%.

•The width of a rectangular channel is its

breadth

Special importance attaches to

prismatic channels

: those that have a constant cross sectional shape,

longitudinal slope, and alignment. The generators of prismatic channels are parallel straight lines. The

most common prismatic channel cross sections are trapezoids, rectangles, and partially full circles.

Constructed channels often consist of long prismatic reaches connected by short transition sections.

Natural channels are never prismatic, although the assumption that they are is sometimes tolerable.

The direction of ﬂow is indicated by the spatial variable

; the two coordinates orthogonal to each

other and to

are called

and

. For a parallel ﬂow, the total volume of water ﬂowing per unit time

across an orthogonal ﬂow area, is the

ﬂowrate

discharge

, given by

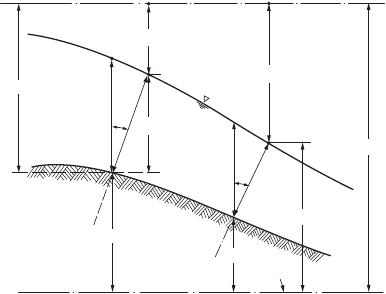
FIGURE

30.1

Deﬁnitions:

, depth of stream;

, thickness of stream; z, bottom elevation;

, angle between channel

bottom and horizontal;

speciﬁc energy;

piezometric head and water surface elevation;

total head;

velocity head. Subscripts denote ﬂow area.

z = 0

datum

/2g

cosq

/2g

Open Channel Hydraulics

-3

(30.1)

where

(

x, y

, z

) is the local

-velocity at coordinates

x, y

, z

and time

The integral extends across the whole ﬂow area, and

is the

mean velocity

Classiﬁcation of Flows

Steady ﬂows

are time invariant and

unsteady ﬂows

are time dependent. Because open channel ﬂows are

typically turbulent, and thus inherently unsteady in detail, these terms are understood to apply to the

time-averaged components of the ﬂow variables.

Uniform

normal ﬂow

is the important special case

of constant thickness ﬂow in a prismatic channel. More common is

gradually varied ﬂow

in which

streamwise changes in the ﬂow area are sufﬁciently gradual that the time-averaged streamlines can be

assumed parallel. When the deviation of the time-averaged streamlines from being parallel cannot be

neglected, the ﬂow is termed

rapidly varied

. If the ﬂowrate changes along the direction of ﬂow (due to

addition or withdrawal of liquid) it is a

spatially varied ﬂow

Flow Regimes

Since free surface ﬂows are affected by gravitational, viscous, and surface tension forces, the relevant

dimensionless parameters are the Froude number, the Reynolds number, and the Weber number. The

most important of these is the Froude number,

where

, the celerity, is the velocity of propagation

of a small amplitude, shallow water gravity wave. For an arbitrary cross section

c = (g D)

1/2

. For a

rectangular cross section this reduces to c = (g y)

1/2

. The Froude number compares the speed of the liquid

to the speed at which small disturbances of the free surface propagate relative to the liquid. When Fr < 1,

small disturbances can propagate upstream as well as downstream, and the ﬂow regime is called subcritical,

tranquil, or streaming. When Fr > 1, small disturbances are too slow to propagate upstream. This regime

is called supercritical, rapid, or shooting. This distinction is of great practical importance because if the

ﬂow at a given cross section is supercritical, downstream events cannot inﬂuence the ﬂow unless they

are large enough to force the ﬂow to change to subcritical. The rare case of Fr = 1 is called critical ﬂow.

The Froude number can also be interpreted as being proportional to the square root of the ratio of the

inertial forces to the gravitational forces. Some authors deﬁne the Froude number as the square of the

present deﬁnition.

The Reynolds number may be deﬁned for open channel ﬂow as Re = 4reRV/m, where r is the mass

density and m is the dynamic viscosity of the liquid. (Many authors omit the factor of 4.) The Reynolds

number is proportional to the ratio of inertial forces to viscous forces. For Re < 2000, open channel ﬂow

is laminar. When Re exceeds about 8000, it is turbulent. At intermediate values the ﬂow is transitional.

In hydraulic engineering practice, laminar and transitional ﬂows are rare, occurring mostly in shallow

sheet storm runoff from roofs and pavements.

The Weber number for open channel ﬂow is deﬁned as We = reDV

/s, where s is the surface tension

coefﬁcient. The Weber number is a measure of the ratio of inertial forces to surface tension forces.

Although threshold values have not been determined, the high values typical of hydraulic engineering

applications indicate that surface tension effects may be neglected.

30.2 Balance and Conservation Principles

As shown in Chapter 28, the fundamental principles of nature may be written in a balance form for an

arbitrarily speciﬁed region called a control volume. In this chapter we consider a control volume which

contains all of the liquid between an upstream ﬂow area (A

) and a downstream ﬂow area (A

). The

lateral boundaries coincide with the wetted channel lining and the free surface.

Qxt vxy z tdydz V x t A x t

,(,,,) ,,

()

¢¢ ¢¢

()()

ÚÚ

30-4 The Civil Engineering Handbook, Second Edition

Conservation of Mass

The principle of conservation of mass states that the time rate of change of mass inside a control volume

is equal to the balance between the inﬂowing and outﬂowing mass through the control surfaces. For

liquids of constant density, conservation of mass implies conservation of volume. In the case of steady

ﬂow in a control volume which contains all of the liquid between an upstream ﬂow area and a downstream

ﬂow area, we have Q

= Q

out

= Q or

(30.2)

This is known as the continuity equation. For a rectangular channel of constant breadth

(30.3)

where q = Q/b is the speciﬁc ﬂowrate or ﬂowrate per unit breadth.

Conservation of Momentum

The principle of conservation of momentum states that the time rate of change of the momentum inside

a control volume is equal to the sum of all the forces acting on the control volume plus the difference

between the incoming and outgoing momentum ﬂowrates. Note that it is a vector equation. For steady

ﬂow with constant density along a straight channel, the streamwise component of the momentum

equation for a control volume that contains all of the liquid between an upstream ﬂow area and a

downstream ﬂow area becomes

(30.4)

where SF ¢ is the sum of the streamwise forces on the control volume.

These forces typically include the hydrostatic pressure forces on the ﬂow areas, the streamwise com-

ponent of the weight of liquid within the control volume, and the streamwise force exerted by the wetted

surface of the channel. b is called the momentum correction factor and accounts for the fact that the

velocity is not constant across the ﬂow areas:

(30.5)

The value of b is 1.0 for a ﬂat velocity proﬁle, but its value increases as the irregularity of the velocity

distribution increases.

Piezometric Head

As a ﬁrst application of the momentum equation, consider the control volume shown in Fig. 30.2 having

sides AB and DC of length Dx parallel to the streamlines, sides AD and BC of length Dy ¢, and breadth

Dz¢ normal to the page. Since the momentum ﬂuxes and shears along the faces AB and DC have no

normal component, the net pressure force in the y¢-direction (∂p/∂y¢) Dy ¢D xDz¢, must be balanced by

the normal component of the weight of the liquid in the control volume r gDxDy ¢Dz¢cosq =

r gDxDy¢Dz¢(∂z/∂y¢), thus ∂/∂y¢[z + p/(r g)] = 0.

Integration gives

(30.6)

where g =r g is the speciﬁc weight of the liquid

h =the elevation of the free surface

QAV AV==

11 2 2

Vd V d

11 2 2

()

FQVVrb b

22 11

vdA

h+=

Open Channel Hydraulics 30-5

The sum of the elevation head and the pressure head, called the piezometric head, has the same value

at all the points of the same cross section of a parallel ﬂow. This value is the elevation of the free surface

for that cross section. This result is of fundamental importance for open channel hydraulics and suggests

two corollaries: the pressure distribution within a given cross section of a parallel ﬂow is hydrostatic, and

the free surface proﬁle of a parallel ﬂow may be deﬁned as its piezometric head line or hydraulic grade line.

Boundary Shear

Apply the streamwise momentum Eq. (30.4) to a control volume that contains all of the liquid contained

between an upstream ﬂow area and a downstream ﬂow area in a prismatic channel. For uniform ﬂow

the momentum ﬂowrates and the pressure forces on the entry and exit faces of the control volume cancel.

Therefore the streamwise component of the weight of the ﬂuid in the control volume must be balanced

by the shear force acting on the wetted perimeter. Thus, if t is the average shear stress on the channel

lining, g A Dx sinq = t PDx, or

t = g R sinq = g R S (30.7)

where S = sinq is the bottom slope of the channel.

Because the ﬂow is uniform, S is also the slope of the piezometric head line and the total head line.

When Eq. (30.7) is applied to gradually varied ﬂow, S is interpreted as the slope of the total head line

and is usually called the friction slope.

Total Thrust and Speciﬁc Force

Consider a control volume containing all of the liquid between upstream ﬂow area A

and downstream

ﬂow area A

in a prismatic channel. In this case the ﬂow depth may vary in the streamwise direction.

The forces in the streamwise momentum Eq. (30.4) are the hydrostatic forces on the end surfaces and

the component of the weight of the liquid in the ﬂow direction. Friction forces are neglected. The

momentum equation in the ﬂow direction is thus

(30.8)

where d

represents the vertical depth of the centroid of ﬂow area A

below the free surface of A

, and

W is the weight of the liquid in the control volume.

FIGURE 30.2 Forces and momentum ﬂowrate on a ﬂuid element.

gd gd q b r b r

11 2 2 2

AAW QAQA-+ = -sin

30-6 The Civil Engineering Handbook, Second Edition

This can be rearranged as

(30.9)

where the expression in parentheses is called the total thrust, F.

(30.10)

The total thrust is the sum of the hydrostatic thrust gdA, which increases with ﬂow thickness, and the

momentum ﬂowrate brQ

/A, which decreases with ﬂow thickness if Q and b are assumed constant.

Therefore the total thrust reaches a minimum at the critical stream thickness, d

, as illustrated in Fig. 30.3.

This value can be found by setting the derivative of F with respect to d equal to zero with the result that

(30.11)

For most cross sections, Eq. (30.11) must be solved numerically. The function F/g is known variously

as the speciﬁc force, momentum function, or thrust function.

Balance of Mechanical Energy

The mechanical energy of a body of mass m is the sum of its gravitational potential energy mgz and of

its kinetic energy mv

/2, where z is the elevation of the mass m above a reference datum. The principle

of conservation of mechanical energy states that the time rate of change of the mechanical energy in a

control volume is equal to the net ﬂowrate of mechanical energy at the inlet and outlet sections, plus

the work done by the pressure forces at the inlet and outlet sections, plus the loss of mechanical energy

in the control region. For the steady ﬂow of an incompressible liquid through a control volume where

the ﬂow is parallel and normal to a single plane inﬂow area and a single plane outﬂow area, the mechanical

energy equation in terms of head becomes

(30.12)

where h

is the head loss and a is the kinetic energy correction factor that accounts for the nonuniformity

of the velocity across the ﬂow area.

FIGURE 30.3 Total thrust curve.

gd b r gd b r q

11 1

1222

AQA A QAW+

()

- sin

FAQA=+gd br

AT Q g

()

bqcos

++ =++ +

Open Channel Hydraulics 30-7

(30.13)

The value of a is 1.0 for a ﬂat velocity proﬁle, but increases as the velocity proﬁle becomes more

irregular.

The total head H is deﬁned as the sum of the elevation head, pressure head, and velocity head, or as

the sum of the piezometric head and the velocity head.

(30.14)

Therefore Eq. (30.12) states that the total head at cross section 1 exceeds that at cross section 2 by the

head loss between the sections. In terms of the variables shown in Fig. 30.1, Eq. (30.12) can be written as

(30.15)

Speciﬁc Energy

Bakhmeteff (1932) ﬁrst emphasized the importance of the quantity E, where

(30.16)

which he called the speciﬁc energy. (Because of its dimensions, E is more properly called speciﬁc head.)

In terms of the speciﬁc energy, Eq. (30.12) becomes

(30.17)

which shows that the speciﬁc energy is conserved when h

= z

– z

, i.e., in uniform ﬂow. It is this property

that gives the speciﬁc energy its importance.

Equations (30.16) and (30.17) are the foundations for the calculation of gradually varied water surface

proﬁles. Given Q, q, a

, d

, and the geometry of cross-section 1, E

can be evaluated using Eq. (30.16).

Then Eq. (30.17) can be solved for E

, if an estimate of the head losses h

is possible. Once E

is known,

Eq. (30.16) can be solved for d

Equation (30.16) shows that E is the sum of two terms. Assuming that a and Q are constant, the ﬁrst

term increases and the second decreases as d increases. Hence there is a critical thickness, d

, for which E

is a minimum. By differentiating Eq. (30.16) with respect to d and equating the derivative to zero, the

following condition for critical ﬂow is obtained.

(30.18)

The expression A

/T is called the section factor for critical ﬂow. For most cross sections, Eq. (30.18)

must be solved numerically. Note that the critical depth is independent of the channel slope and rough-

ness. It is interesting to recognize that the critical thickness which satisﬁes Eq. (30.18) differs from that

which satisﬁes Eq. (30.11) unless a = b, which is true only for a ﬂat velocity proﬁle. In practice, the

difference is usually negligible; and Eq. (30.18) is used in the calculation. The velocity corresponding to

, called the critical velocity, V

, is given by

(30.19)

vdA

=+ + =+

zd V g zd Vgh

L11 1 11

22 2 22

22++

()

=+ +

()

+cos cosqa qa

Ed V g d Q gA=+

()

cos cosqa qa

222

zE z Eh

L112 2

+=++

AT Q g

()

aqcos

Vg D

()

cosqa