Yamaguchi H. Engineering Fluid Mechanics (Fluid Mechanics and Its Applications)
Подождите немного. Документ загружается.

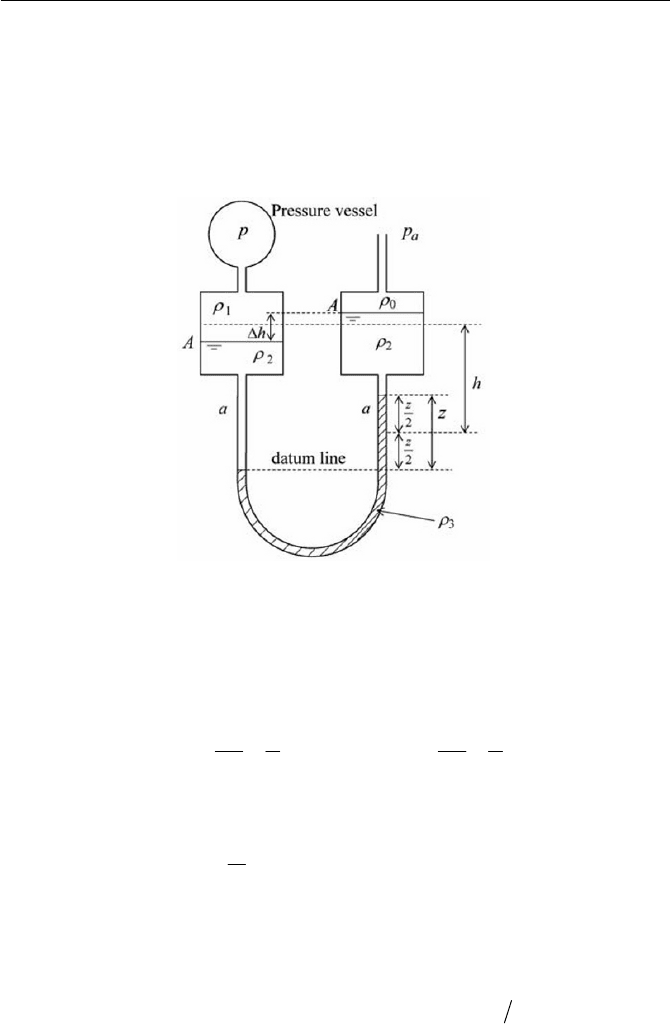
Exercise 91
Ans.
There is a relationship of volume equality between the reading z of
liquid
3
U
and the level difference
h
of liquid
2
U
hAaz
(1)
Fig. 3.10 Micromanometer
Taking the datum line at the lowest level of the manometric liquid
3
U
and
the mean level difference as
h , we have the pressure balance equation as
follows
z
zh
hp
zh
hhp
a
gggg
3221
2222
UUUU
¸
¹
·
¨
©
§
'
¸
¹
·
¨
©
§
'
' (2)
Using the relationship given by Eq. (1), Eq. (2) can be reduced to
z
A
a
pp
a
g
»
¼
º
«
¬
ª
2312
UUUU
(3)
Thus, by reading a scale of
z , measurement of the pressure
p
can be
achieved. Particularly with this manometer, small pressure differences
a
pp are accurately measurable by choosing the density difference
12
U
U
and
23
U
U
smaller, as well as keeping
Aa
small. A ma-
nometer with this arrangement is called micromanometer.
'
'

92 3 Fluid Static and Interfaces
Exercise 3.2 Hydrostatic Paradox
Obtain overall force
F
exerted by a liquid column in the static equilibrium
for cases (a), (b), (c), and (d) in Fig. 3.11.
Ans.
For all cases, we try to obtain the pressure on the bottom surface A .
From the hydrostatic equation Eq. (3.1.2) without
r
a and
I
, in which no
linear acceleration and no rotation of fluid are conditioned, we have
g
U
p
(1)
Since the body force term
g
U
can be written by a potential function
zg
U
I
under the earth’s gravity field, Eq. (1) becomes
0
(2)
Bearing in mind
I
p . Consider the integral of from point 0 to 1
as
³³
1
0
1
0
0rdd
(3)
This also yields
>@
011
1
0
1
0
011
1
0
II
IIII
³³
a
a
pp
ppppdd
(4)
Thus, from Eqs. (3) and (4), we know
011
I
I
a
pp
(5)
1
p
in Eq. (5) is independent from the path line of the integral, and only de-
termined by the deference between the relative points 0 and 1. Resulting
from Eq. (5):
hp
zzp
zzpp
a
a
a
g
g
gg
U
U
UU
01
011
(6)
Thus, the overall force
F
is
za
A
Ahp
dSp
e
nF
ˆ
ˆ
g
U
³
(7)
)
))
))
)
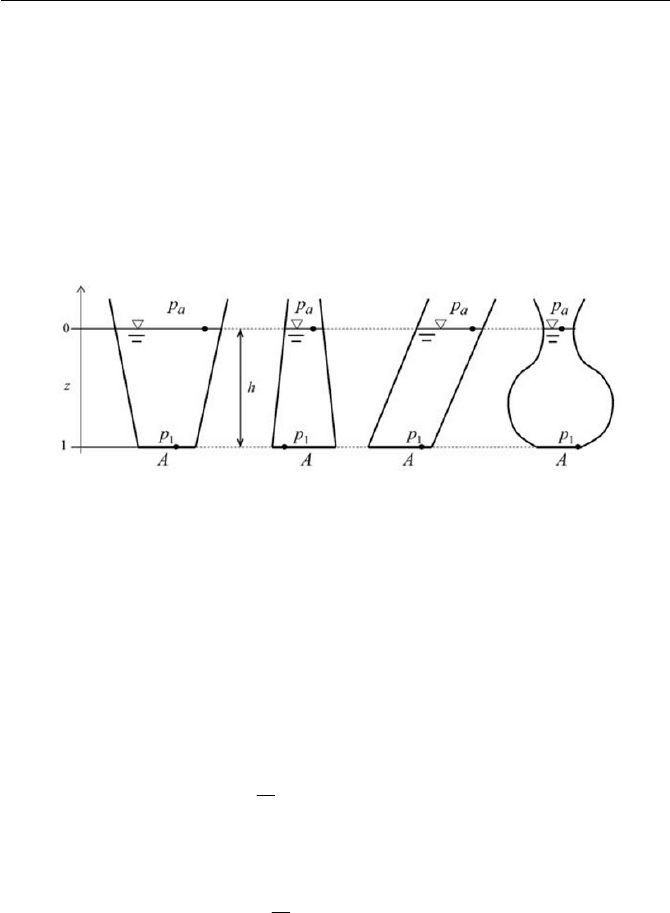
Exercise 93
By the same token, for the gauge pressure force
G
F we can write
zG
hA eF
ˆ
g
U
(8)
The overall force
F
acting on the surface A is the same for (a –d). This
is called the hydrostatic paradox. Equation (8) is equivalent to Eq. (3.1.18),
in which
G
h is set as hh
G
since the area A is horizontal. Equation (6)
can also be proven by the Bernoulli equation, setting the velocity head at zero.
(a) (b) (c) (d)
Fig. 3.11 Hydrostatic paradox
Exercise 3.3 Pressure at High Altitude
Estimate the pressure at m10000 above the sea level, assuming;
(i) linearly varying temperatures
0
TazT
(1)
and
(ii) polytropic changes
const.
1
¸
¸
¹
·
¨
¨
©
§
n
p
U
(2)
We may use the ideal gas law for the equation of the state of air
RTp
¸
¸
¹
·
¨
¨
©
§
U
1
(3)
Considering the specific gas constant KJ/kg287
R . For Eqs. (1) and
(2) the constants are the lapse rate K/m106500
2
u .a , the standard tem-
perature at sea level which is
K288
0
T , the polytropic constant for air is
2351. n and the standard atmospheric pressure is
25
N/m100131 u .
a
p .

94 3 Fluid Static and Interfaces
Ans.
For case (i) and (ii), the hydrostatic equation Eq. (3.1.3) can be applied,
referring to Fig. 3.1 for
z increasing as follows
g
U
dz
dp
(4)
(i) From the equation of state given by Eq. (3), the density is expressed as
RT
p
U
(5)
Since the temperature
T
in Eq. (5) varies linearly for increasing altitude z
as shown in Eq. (1), the density is represented as
0
TazR
p
U
(6)
The density variation of Eq. (6) is then substituted into the hydrodynamic
equation of Eq. (4), which gives
dz
TazRp
dp
0
1
g
(7)
This can be integrated to give a solution for
1
p
as follows
³³
dz
TazRp
dp
0
1g
(8)
Thus we can calculate
25
287106500
819
2
5
0
0
1
N/m102640
288
10000106500288
100131
2
u
¸
¹
·
¨
©
§
uu
u
¸
¸
¹
·
¨
¨
©
§
uu
.
.
.
.
.
aR
a
T
azT
pp
g
(9)
(ii) Applying the polytropic atmospheric change given by Eq. (2), the rela-
tion between pressure and density at any altitude can be written as

Exercise 95
n
a
p
p
1
0
¸
¸
¹
·
¨
¨
©
§
UU
(10)
The density variation of Eq. (10) is then substituted into the hydrostatic
equation of Eq. (4), which gives
dz
p
p
dp
n
a
n
g
0
1
1
1
U
¸
¸
¹
·
¨
¨
©
§
(11)
This can be integrated to give a solution for
1
p as follows
³³
¸
¸
¹
·
¨
¨
©
§
dz
p
p
dp
n
a
n
g
0
1
1
1
U
(12)
Hence, we can calculate
25
12351
2351
5
1
0
1
0
0
1
N/m102640
10000
288287
819
2351
12351
1100131
1
1
1
1
u
¸
¹
·
¨
©
§
u
u
u
¸
¹
·
¨
©
§
¸
¸
¹
·
¨
¨
©
§
.
.
.
.
.
.
.
n
n
a
n
n
a
z
RTn
n
p
z
pn
n
pp
g
g
U
(13)
It is further thought that, from
1
p expressed in Eq. (13), the density at z is
easily obtained by Eq. (10) as
1
1
0
0
1
1
¸
¸
¹
·
¨
¨
©
§
n
RT
z
n
n
g
UU
(14)
With the equation of state given by Eq. (3), the temperature variation can
be calculated as follows

96 3 Fluid Static and Interfaces
0
0
0
1
1
1
Tz
Rn
n
z
RT
n
n
TT
¸
¹
·
¨
©
§
»
»
¼
º
«
«
¬
ª
¸
¸
¹
·
¨
¨
©
§
g
g
(15)
Equation (15) indicates that the temperature variation for an elevation z is
linear and the lapse rate can be calculated by those values given for n ,
R
,
0
T , yielding
K/m106500
1
2
u
.
Rn
n
a
g
(16)
In the troposphere (the nearest earth atmosphere to sea level), the pres-
sure variation is linear at an average rate of
650. C
q
per 100 m to a dis-
tance of 1000 m in the polar region to 14000 m in the equatorial region.
According to the calculation shown above, an airplane flying with an alti-
tude of 10000 m may experience 0.26 degrees of atmospheric pressure
with a temperature of –50
C
q
.
Exercise 3.4 Forces on Tank Wall
Find the forces on the tank walls, as shown in Fig. 3.12, for a portion of a
vessel filled with a liquid. Also determine the center of pressure in each
case. Consider first the general wall shape with unit depth as depicted in
Fig. 3.12(a), then calculate the specific configuration as shown in Fig.
3.12(b). In the case of Fig. 3.12(b), the shape of the tank walls is expressed
by following relation, provide the answer.
1
2
2
1
00 dzandaxx
a
d
z dddd
;
Ans.
Let us consider a general approach in the
x
– z plane for an arbitrary
curved surface, as schematically shown in Fig. 3.12(a). The force acting on
the wall element
dS is found to be
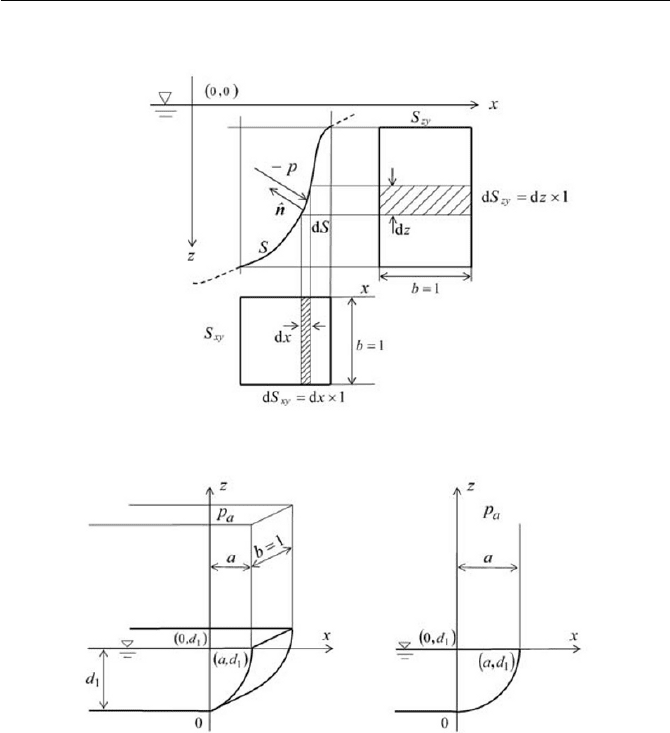
Exercise 97
(a)
( b)
Fig. 3.12 Pressure on curved walls
zzxx
zx
zxyxzy
zx
dFdF
pdxpdz
pdSpdS
dSp
dSpd
ee
ee
ee
ee
nF
ˆˆ
ˆˆ
ˆˆ
ˆˆ
ˆ
ED
coscos
(1)
D
cos and
E
cos are the direction cosines for n
ˆ
. Thus, the force acting on
the surface area
S is calculated by integrating Eq. (1) as

98 3 Fluid Static and Interfaces
zzxx
zzxx
FF
dFdF
ee
eeF
ˆˆ
ˆˆ
³
(2)
The force
F
has two components
³
pdzF
x
and
³
pdxF
z
in the
direction of
x
and z respectively. The magnitude of
F
and the action
angle
D
(the inclination of this force to the horizontal plane) are
22
zx
FF F and
x
z
F
F
1
tan
D
(3)
Setting
z
p
g
U
, the gauge pressure of
x
F and
z
F can be calculated as
follows:
zyGx
SzzdzF gg
UU
³
(4)
VzdxF
z
gg
UU
³
(5)
G
z is the centroid of the projected area
zy
S , and V is the volume of liquid
contained vertically on the surfaces.
The center of pressure
C
x can be directly obtained by the moment bal-
ance equation given by Eq. (3.1.19) as repeatedly written by
dSp
S
C
³
u u nxFx
ˆ
(6)
z
C
x
CC
zx eex
ˆˆ
. Substituting Eqs. (1) and (2) into Eq. (6), we can obtain
the coordinates of the center of
C
x as
z
S
C
F
pdxx
x
³
(7)
x
S
C
F
pdzz
z
³
(8)
Again considering
z
p
g
U
together with Eqs. (4) and (5), we can get
C
x as

Exercise 99
V
I
V
zdxx
x
xz
C
³
g
g
U
U
(9)
zyG
z
zyG
C
Sz
I
Sz
zdxz
z
³
g
g
U
U
(10)
Now we can consider the problems for Fig. 3.12(b), knowing the gen-
eral relations of Eqs. (1 – 10). Denote
p as the gauge pressure, based on
the level of liquid, i.e.
gz
U
p
. Note that the surrounding pressure
a
p is
atmospheric and the force acting on the inner surface of the tank wall is
subject to liquid pressure. Also, denoting that the surface
zy
dS is negative
and
xy
dS is positive, the force on the wall is thus calculated as follows, ac-
cording to Eqs. (4) and (5)
zyG
d
d
x
Sz
d
d
bdbzbzdzF
g
g
ggg
U
U
UUU
u
¸
¹
·
¨
©
§
»
¼
º
«
¬
ª
³
1
2
2
1
2
1
1
1
2
1
0
2
0
1
1
(11)
V
ad
bdxx
a
d
bzdxF
aa
z
g
g
gg
U
U
UU
¸
¹
·
¨
©
§
³³
1
0
2
2
1
0
3
1
(12)
22
zx
FFF and
x
z
F
F
tan
D
(13)
For the center of pressure
C
x , we can calculate
C
x and
C
z from Eqs. (9)
and (10) as follows
–1
100 3 Fluid Static and Interfaces
adxx
a
d
x
VV
xzdx
x
a
a
C
4
31
0
2
2
1
0
¸
¹
·
¨
©
§
³
³
(14)
and
1
2
1
3
1
0
2
3
2
2
1
3
1
1
d
d
d
Sz
dzz
z
zyG
d
C
³
(15)
Consequently, the horizontal forces of
x
F are all the same in any wall
shape, so that the overall force F, the action angle
D
and the center of
pressure
C
x are determined by
z
F , which is similarly the volume of liquid
contained vertically on the surface of the walls.
In obtaining forces and the center of pressure for a required geometry,
one must not be too anxious about the centroid and the moment of inertia
or the product of inertia, but simply carry on the integration for Eqs. (4),
(5), (7) and (8) to get the results for the required geometry.
Exercise 3.5 Stability of Floating Objects
Discuss the criteria of stable floatation for a cylindrical object with a slid-
ing weight inside, if the body is tilted slightly in the horizontal direction as
shown in Fig. 3.13 (a). Consider the following: (i) when the weight is at
the bottom; and (ii) when the weight is slid forward to the top of the cylin-
der. Let
W be the representative weight of the floating object, and let
D
be the diameter of the cylinder. Use
1
D
D
as the tilt angle and
U
as
the density of the liquid.
Ans.
We first consider that the floating object is in equilibrium vertically be-
fore tilting, so that the floating object is vertically stable and FW ,
where
F
is the buoyant force acting at C and W is the total weight rep-
resented by the weight at the center of gravity
G
. Let
l
be the length of
the cylinder of the submerged portion, and let
a be the distance of G
from the liquid level as shown in Fig. 3.13(a).
With a small tilt angle
D
, the equilibrium may be stable or unstable,
depending upon the resultant body couple due to tilting. If the body couple
