Yamaguchi H. Engineering Fluid Mechanics (Fluid Mechanics and Its Applications)
Подождите немного. Документ загружается.

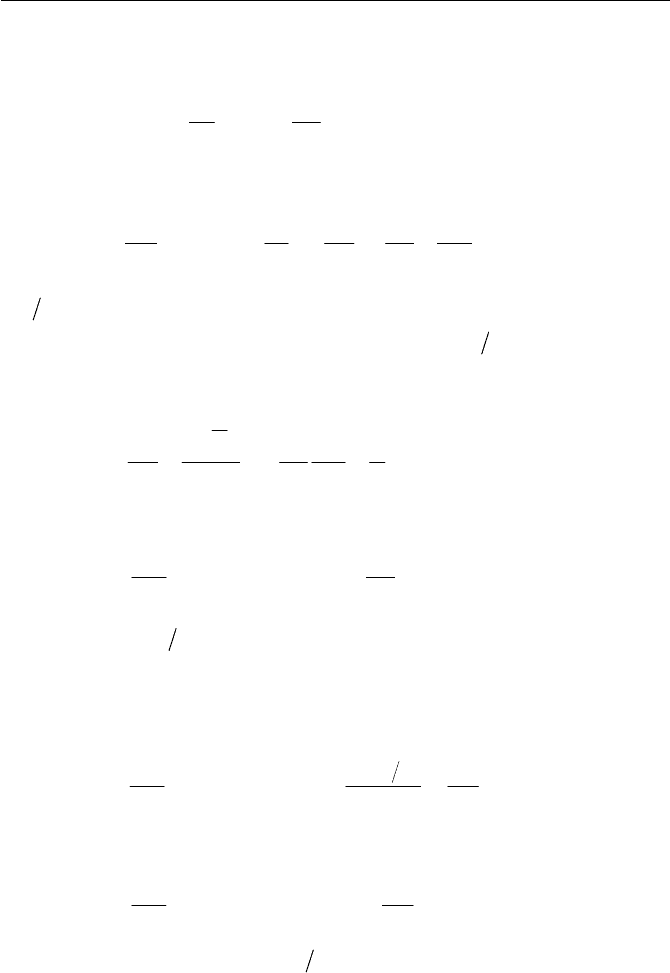
60 2 Conservation Equations in Continuum Mechanics
Since
Du
in Eq. (2.5.18) can be regarded as the total differentiation by the
two thermodynamic properties
v and
T
, it then yields
dTdv
vT
T
u
v
u
Du
¸
¹
·
¨
©
§
w
w
¸
¹
·
¨
©
§
w
w
(
2.5.19)
From Eq. (2.5.6), we can write Eq. (2.5.19) as
Dt
DT
T
u
Dt
Dv
v
s
Tp
Dt
Du
v
T
¸
¹
·
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
¸
¹
·
¨
©
§
w
w
(2.5.20)
T
vs ww is obtained from the Maxwell equation of Eq. (2.5.10). The mate-
rial derivative of
v
in Eq. (2.5.20) in a limit of
U
G
1 v can be written as
follows
u
¸
¸
¹
·
¨
¨
©
§
ȡDt
D
Dt
ȡ
D
Dt
Dv 11
1
2
U
U
(
2.5.21)
Thus, using Eqs. (2.5.20) and (2.5.21), Eq. (2.5.18) can be rewritten as
b
T
p
T
Dt
DT
ȡc
v
v
U
¸
¹
·
¨
©
§
w
w
uuIJq ᧶
(
2.5.22)
(2.5.16). With a similar manipulation, using the enthalpy h defined in Eq.
(2.5.15), i.e. pvhu
, into Eq. (2.5.18), we can obtain the following ex-
pressions for the conservation equation of energy as follows;
ȡb
Dt
Dp
T
ȡ
Dt
DT
ȡc
p
p
»
¼
º
«
¬
ª
w
w
ln
1ln
uIJq
(
2.5.23)
and
ȡb
Dt
Dp
T
Dt
DT
ȡc
T
p
E
uIJq
(
2.5.24)
p
c defined by Eq. (2.5.17). In Eq. (2.5.24),
T
E
is the coefficient of ther-
mal expansion, which is made apparent by
᧶
Here, the term
v
Tu ww
was replaced by the specific heat
v
c
given by Eq.
We can now see that the term
p
Th ww was replaced by the specific heat

2.5 Thermodynamic Relations 61
p
T
T
¸
¹
·
¨
©
§
w
w
U
U
E
1
(
2.5.25)
Note that for an ideal gas
T
T
1
E
and for a liquid,
T
E
is usually smaller
than
T1
. The enthalpy change dh is also written by using the quantity
T
E
,
and it can be thus derived from the thermodynamics relationship;
U
E
dp
TdTcdh
T
p
1
(2.5.26)
In the case of an incompressible flow, i.e. 0 u , or if the pressure
variation is supposed to be small enough that the term
DtDp
in Eq.
(2.5.23) can be disregarded, which is really limited to nearly incompressi-
ble material, the conservation equation of energy will become
b
Dt
DT
c
p
UU
uIJq :
(
2.5.27)
It should be kept in mind that in a compressible flow or a nearly in-
compressible flow of continuum, the specific heat is
p
c . In most practice
flows of nearly incompressible materials, it is satisfactory to say that
v
p
cc | .
Considering Eq. (2.4.12), the heat transfer
q to a fluid particle is con-
sidered to be carried out by heat conduction through the surface. In this
case
q is given by Fourier’s law;
Tk
c
q
(2.5.28)
Here,
c
k is the thermal conductivity, noting that
n
ˆ
is directed toward the
surface in Eq. (2.4.12). It is further to be noted that Eq. (2.5.28) stands for
homogeneous and non-diffusing mixtures. Thus, using Eqs. (2.5.28),
(2.5.27) is written
bTk
Dt
DT
c
cp
UU
uIJ :
(
2.5.29)
Moreover, for a constant
c
k , Eq. (2.5.29) can be further simplified:
pp
c
b
c
Tk
Dt
DT
¸
¸
¹
·
¨
¨
©
§
uIJ :
U
D
1
2
(
2.5.30)

62 2 Conservation Equations in Continuum Mechanics
where,
pc
ckk
U
D
is called the thermal diffusivity. Equation (2.5.30)
gives an equation for the temperature field of the flow.
Exercise
Exercise 2.1 Mass Conservation
Consider a steady state flow in a branching channel, entering inlet section
1 and leaving sections 2 and 3 with mean velocity vectors
1
u ,
2
u and
3
u
respectively, normal to the cross sectional area (surface element) of
1
A ,
2
A and
3
A as shown in Fig. 2.6. Write the continuity equation of the sys-
tem. If outlet section 3 is blocked, what will the continuity equation be?
Ans.
Using the continuity equation of (2.1.5) for the steady state, i.e.
0 ww t
, the integral equation may be recovered by Gauss’s divergence
theorem
0ේ
SV
ddV Suu
UU
(
1)
Applying Eq. (1) to the current system gives
0
321
332211
SAAA
ddSudSudSu Su
UUUU
(
2)
Since at the channel surface there is a relationship of Su dA , which is to
say that there will be no flow across the wall, the last term of Eq. (2) van-
ishes. So that
333222111
uAuAuA
U
U
U
(3)
This is the continuity equation of the system. If 0
3
u , Eq. (3) becomes
222111
uAuA
U
U
(4)
Exercise 63
Fig. 2.6 Flow in branching channel
21
mm
(5)
Equation (5) indicates that the mass flow rate m
is conserved from the
inlet to the outlet of the channel.
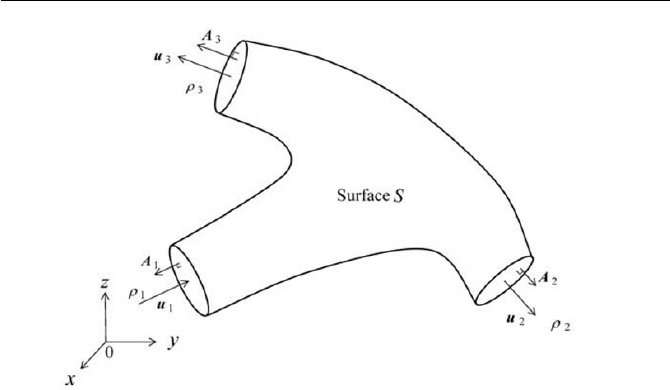
Exercise 2.2 Conservation of Linear Momentum
A steady state flow is passing through a section of a channel as shown in
Fig. 2.7. The forces
1
F and
2
F acting on the control volume (the channel
volume) are due to the surface force and body force respectively. Assum-
ing the inlet’s mean velocity
1
u and outlet’s mean velocity
2
u are respec-
tively parallel to the surface element
1
A
and
2
A
, write a linear momentum
equation of this system.
Ans.
For steady state of flow, the conservation equation of linear momentum
can be written by referring to Eq. (2.2.4) as follows
g
U
U
Tuu
(1)
Using the volume integral in the equation and applying Gauss’s divergence
theorem we have
and

64 2 Conservation Equations in Continuum Mechanics
Fig. 2.7 Forces acting on a section of channel
21
FFSuu
³³³
VSV
dVdVd g
UU
T
(2)
The left hand side of Eq. (2) is calculated as follows when applied to the
system
22221111
21
uu
SuuSuuSuu
AuAu
ddd
SAA
UU
UUU
³³³
(3)
The integral over the channel wall becomes null due to no cross flow
through the wall. Therefore, Eq. (2) can be reduced to the form
211122
FFuu mm
(4)
With the continuity equation from Exercise 2.1, i.e.
21
mmm
, we can
derive the conservation equation of linear momentum for this system as
follows
2112
FFuu
m
(5)
Equation (5) is nothing but Newton’s second law of motion, stating the
change of momentum is equal to the sum of forces applied to the system.
Exercise 65
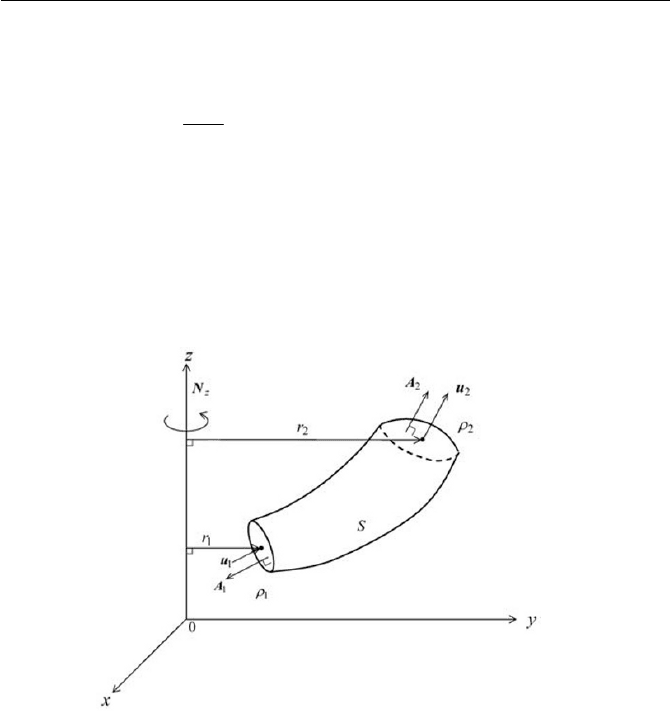
Exercise 2.3 Torque on Control Volume
When considering non-polar fluid, the conservation equation of the angu-
lar momentum given by Eq. (2.3.1) can be alternatively expressed by the
general form
N
L
Dt
D
(1)
where L is the net angular momentum acting on a control volume (in the
Eulerian description) and N is defined as the net torque exerted on the
system. Verify the steady torque
z
N around the
z
axis due to the change
of
L , where L is obtained from
dV
V
³
u uxL
U
(2)
See Fig. 2.8 for the flow configuration.
Ans.
With the aid of Reynolds’ transport theorem, to the left hand side of Eq.
(1) we have
³³³
u
w
uw
u
SVV
d
t
dV
Dt
D
Suuxn
ux
ux
U
U
U
ˆ
(3)
Additionally, for a steady state, i.e.
0 ww t
, Eq. (3) will be
dS
Dt
D
S
nuux
L
ˆ
u
³
U
(4)
Equation (4) can be integrated, as depicted schematically in Fig. 2.8, to
give the surface of the control volume;
dSdSdS
dS
SAA
S
nuuxnuuxnuux
nuux
ˆˆˆ
ˆ
uuu
u
³³³
³
UUU
U
22221111
21
(5)
Since there would not be any cross flow through the channel wall, the
last term of Eq. (5) vanishes and we have
222111
2222211111
uxux
uxux
L
uu
uu
mm
AuAu
Dt
D
UU
(6)
66 2 Conservation Equations in Continuum Mechanics
Therefore the change of angular momentum around the z axis can be ob-
tained by applying the dot product of
z
ˆ
e
to Eq. (6), which is
tt
z
urmurm
D
t
DL
11122
2
(7)
Note that
t
u
2
and
t
u
1
are the tangential components of the velocity vector
1
u and
2
u respectively, perpendicular to the z axis. Considering the equa-
tion of continuity, i.e.
21
mmm
, we can finally derive the torque
z
N ,
which is given by the following formula;
tt
z
ururmN
1122
(8)
Fig. 2.8 Torque exerted on control volume
From the perspective of engineering application, torque is a very im-
portant parameter to characterize rotating machineries, particularly for the
rotors of turbomachines in fluid engineering. Equation (8) is often referred
to as Euler’s pump or turbine equation, which will be studied in more de-
tail for turbomachines in a few sections of Chapter 4.
Exercise 2.4 Energy Conservation of a System
Consider a control volume as a thermodynamic system, where a perfect
fluid enters from section 1 and leaves from section 2. Velocities
1
u and
2
u
at each section are parallel to the surface elements
1
A and
2
A respectively,
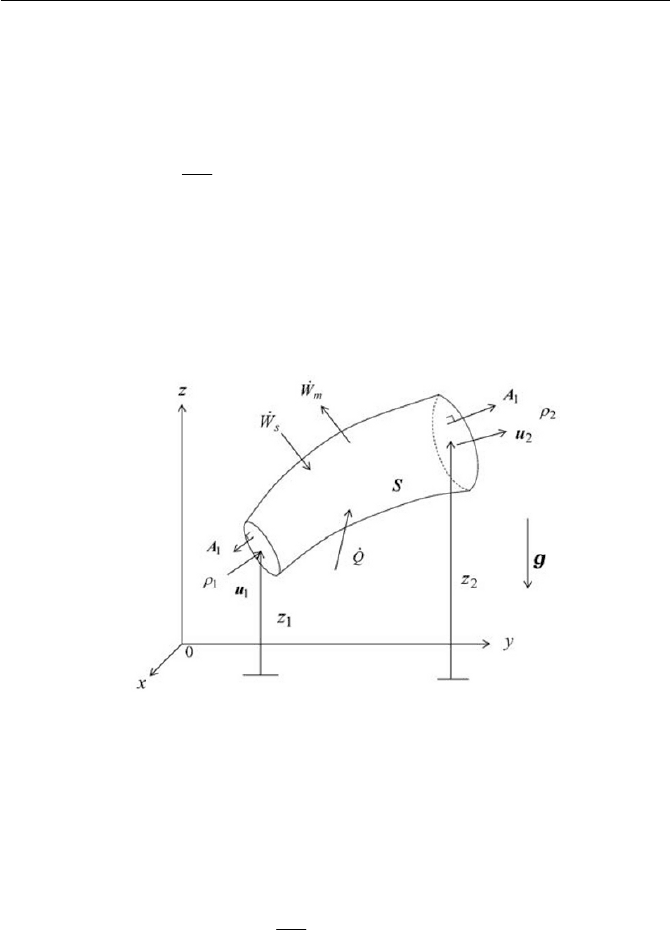
Exercise 67
as shown in Fig. 2.9. If we assume that the system gives mechanical work
m
W
to the surrounding, besides its work input
s
W
to the system, the first
law of thermodynamics in the system may be applied to the system by
writing the conservation of energy as follows
ms
WWQuk
tD
D
(1)
Derive an expression of an energy conservation equation at a steady
state for the system in Fig. 2.9. Note that the minus sign of the mechanical
work done
m
W
by the system is meant to be toward the outside (surround-
ing) of the system and the plus sign of
Q
is heat transferred to the system
from the outside (the surrounding).
Fig. 2.9 Energy conservation of a system
Ans.
We shall derive an expression for the energy balance to the heat input
and the mechanical work by writing
sm
Wuk
tD
D
WQ
(2)
The right hand side of Eq. (2) can be expanded in consideration of Eqs.
(2.4.3) and (2.4.14) as follows

68 2 Conservation Equations in Continuum Mechanics
¸
¹
·
¨
©
§
»
¼
º
«
¬
ª
¿
¾
½
¯
®
³³
³
SV
n
V
s
dVdS
dVu
tD
D
Wuk
tD
D
uut
uu
g
U
UU
2
1
(3)
Furthermore, for the stress vector
n
t , Cauchy’s stress formula of Eq.
(1.6.8) can be applied as
I
ˆ
T
ˆ
p
n
nnt
(4)
Note that the flow is assumed to be a perfect fluid as given by Eq. (1.6.11).
Substituting Eq. (4) into (3) and applying Reynolds’ transport theorem to
the first term of right hand side of Eq. (3) with the condition
0 ww t
yields
¿
¾
½
¯
®
¿
¾
½
¯
®
³³
³
SS
S
m
dSzdS
p
dSuWQ
nunu
nuuuu
ˆˆ
ˆ
g
U
U
U
UU
2
1
(5)
Here, the volume integration of Eq. (3) was transformed into the surface
integral by Gauss’s divergence theorem, and it is noted that the gravita-
tional acceleration
g is given by the potential
zg
g
. Carrying over
the surface integral of Eq. (5) to the control volume, noting that there
would not be any cross flow through the wall of the control volume, but
only through the inlet and outlet sections, as depicted Fig. 2.9, we can ob-
tain
»
¼
º
«
¬
ª
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
¸
¹
·
¨
©
§
ཱ
ཱ
uuzz
pp
uum
zAuzAu
p
Au
p
Au
uAuuAuuAuuAuWQ
m
12
1
1
2
2
2
1
2
2
11112222
1
1
111
2
2
222
111222
2
1111
2
2222
2
1
2
1
2
1
g
gg
UU
UU
U
U
U
U
UUUU
(6)
Here, notations of
ཱ
u and
u are the internal energy per unit mass at the
outlet and inlet respectively (in order to distinguish between the velocity
components and the internal energy). In deriving Eq. (6), the equation of
continuity is used by setting
21
mmm
.

Problems 69
Problems
2-1. Give some examples, in which the equation of continuity given by Eq.
(2.1.5) does not follow; provide reasons as well.
Ans.
>@
etc. process, flow in the reactions Chemical
2-2. In incompressible irrotational flow, the velocity field is entirely de-
scribed by a scalar function of
x
I
, by solving the Laplace’s equa-
tion 0
2
I
. Give proof of this problem.
Ans.
»
»
¼
º
«
«
¬
ª
u u
0ේthatSo
0since0ේandේ
2
I
II
,, uuu
2-3. Write the non-conservation form of the linear momentum given by Eq.
(2.2.7), in Cartesian coordinates system, using
x
, y , z as coordi-
nates and
zyx
uuuu ,, u , ...,,T
xyxx
TT ,
zyx
ggg ,, g , and
p
.
Ans.
>@
7-BAppendix See
2-4. Write the vorticity transport equation given by Eq. (2.2.9) on a two-
dimensional plane (the
x
– y plane), setting
zz
eȦ
ˆ
Z
. Use notations
similar to those of Problem 2-3.
Ans.
»
»
»
»
»
¼
º
«
«
«
«
«
¬
ª
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
»
¼
º
«
¬
ª
w
w
w
w
w
yxyyxx
y
u
x
u
t
D
yx
xx
yyxy
z
y
z
x
z
W
W
WW
ZZ
U
Z
U
2-5. If the stress tensor T has the skew-symmetric part, what care has to
be taken in order to analyze the flow system?
Ans.
»
»
»
¼
º
«
«
«
¬
ª
equations. of system
the toincluded be tohas
equation momentumAngular
