Yamaguchi H. Engineering Fluid Mechanics (Fluid Mechanics and Its Applications)

Подождите немного. Документ загружается.

Exercise

altered. Draw curves of

and

for the diameter of a colloidal particle

of a magnetic fluid. Also compare the results if the effective relaxation

time

is given via the following expression, Martsenyuk et al. (1974)



(1)

Use the following representative values of the properties of a magnetic

fluid, if necessary



Fefor;K

10470 u .K

;

101u f

;

10381



u .





Kerosenefor

;

1020



u .



Ans.

Let the temperature be 25 , i.e.

K29827325  T

appearing in

Eq. (8.1.3) includes the thickness of the surfactant layer, which gives

write



sdV 

(2)

where

102



u is assumed. Thus, the relaxation time due to the Néel

relaxation

given in Eq. (8.1.5) and the relaxation time due to the

Brownian relaxation

given in Eq. (8.1.4) are respectively written as



uuuu



29810381

10470exp10

23359

.. d

(3)

 

2981038110201022

233

uuuuuuu



..d

(4)

The effective relaxation time

can be calculated in Eq. (1), knowing

and

from Eqs. (3) and (4). The curves of Eqs. (1), (3) and (4) are

505

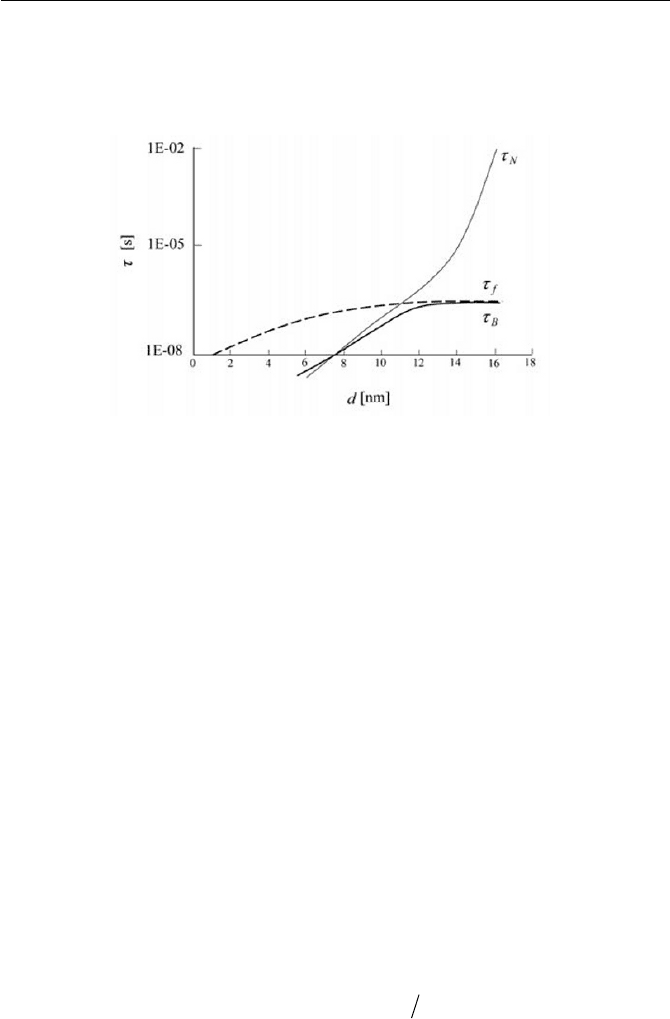
displayed in Fig. 8.3. In a real magnetic fluid, due to a broad size distribu-

tion, the exact evaluation of the relaxation time is difficult. A precise deter-

mination of the relaxation times requires direct experimental observation.

Fig. 8.3

Relaxation of magnetization

Problems

8.1-1 Plot the equilibrium magnetization curve using the Langevin func-

tion given in Eq. (8.1.1). Use values of the parameters, if necessary,

for the particle size

d =10nm at the temperature

=298K with

=0.041 and

=0.04Tesla.

8.1-2 In taking into account the parallelism of

M and H , i.e. HM // , the

induction of

B can be expressed by the magnetic permeability

of a magnetic fluid. Show that

contains the magnetic susceptibil-

ity

and the permeability of free space

Ans.





HǾ

MǾB

8.1-3 Draw a curve for the viscosity ratio

of a magnetic fluid as a

function

under no magnetic field, referring to Eq. (8.1.8). Use a

value of

0.74 for the result.

8 Magnetic Fluid and Flow 506

8.2 Ferrohydrodynamic Equations

In the theory of magnetic fluid, ferrohydrodynamic equations are derived

from a continuum mechanics on a microscopic treatment used to predict its

dynamic behavior, establishing the state of equilibrium, motion and heat

transfer. The concept to establish a dynamic theory of magnetic fluid is

based on the idea that in a magnetic field, nano-scaled magnetic particles

suspended in a non-magnetic fluid media, produces effects that are led by

forces that draw from a dynamic system into a translational and rotational

motion. When a magnetic fluid is in motion, under the applied magnetic

field, the ferromagnetic phase interacts with a carrier liquid through a vis-

cous friction. The establishment of basic equations for magnetic fluid came

from an approach of a quasi-stationery one-phase fluid whose magnetiza-

tion is in equilibrium in any dynamical process, Neuringer and Rosensweig

(1964).

The outline for the governing equations of flow is described below

from the basic concepts of continuum mechanics of polar material. Ferro-

hydrodynamic equations are thereafter derived by the determination of

constitutive equations.

The continuity equation, which is derived from the mass conservation

discussed in Section 2.1, is of the same form for an ordinary fluid

0 

(8.2.1)

The equation of motion derived from the principle of the conservation

of linear momentum is written by an unconstituted form of Cauchy’s equa-

tion of motion, as it appears in Section 2.2, as follows

 T

(8.2.2)

where

is the body force and T is the total stress tensor.

The equation of the internal angular momentum for a polar fluid that is

derived from the conservation law of angular momentum of a polar mate-

rial in Section 2.3 is written below:

 c

(8.2.3)

s is the intrinsic (internal) angular momentum per unit mass, c is the

couple stress tensor,

A is the vector of the tensor T given in Eq. (2.3.9)

and

f is the body couple per unit mass.

507

The energy equation for internal energy

u is derived by the first law

of the thermodynamics for non-(electrically) conductive mediums fol-

lowed by Rosensweig (2002):







HuHB

ȦȦuq

:IHB

İ:T:c:T

(8.2.4)

Ȧ is the average spin angular velocity of particles about their own center

given by the expression:

IȦ

(8.2.5)

Here,

is the moment of inertia per unit of mass for a monodispersion of

spherical particles. Note that B in Eq. (8.2.4) is the magnetic induction

and b is the amount of heat generated per unit mass. It should be kept in

associated with the space the medium occupies, and of which it is given,

where



(8.2.6)

u is the internal energy of the system defined in Eq. (2.4.1) and

is the

permeability of free space, i.e.

mH104

u



. In a magnetic me-

dium,

B , H and M are related by the magnetic polarization relation

given where

MHB 

(8.2.7)

It is noted that in SI units, the magnetic field H has units of





, and

the magnetization

M and the magnetic induction B both have units of

Tesla.Askg





Equations (8.2.2), (8.2.3), and (8.2.4) are unconstituted equations to

which constitutive equations of

T , c , f , A , M and q are to be deter-

mined in order to derive ferrohydrodynamic equations. Each constitutive

equation can be determined such that thermophysical characteristics of

magnetic fluids are satisfied.

–1

8 Magnetic Fluid and Flow

mind that

u in Eq. (8.2.4) is the internal energy exclusive of field energy

508

8.2 Ferrohydrodynamic Equations

In general, magnetic fluids are treated as incompressible and non-

(electrically) conductive mediums. These conditions immediately give the

continuity equation of Eq. (8.2.1) to express

0 

(8.2.8)

The total stress tensor

T in Eq. (8.2.2) may be decomposed by follow-

ing stress tensors:



p TTIT





(8.2.9)

p is the hydrostatic pressure,



T is the viscous stress tensor and is fur-

ther expanded to show, referring to Eq. (2.3.8)



TTT 

(8.2.10)

where

T is the symmetric part and

T is the skew-symmetric part of the

tensor



T and

have their own constitutive equations, which are,

respectively, written with the following formulae:

(8.2.11)

and



ȦA   İİT

]

(8.2.12)

Note that

T is the Newtonian contribution to the symmetric part of the vis-

cous stress tensor. In Eq. (8.2.11),

e is the rate of strain tensor, defined in Eq.

(1.1.16), and

is the apparent viscosity of a suspension in the absence of a

magnetic field, as, for example, it is given in Eq. (8.1.6) or Eq. (8.1.8).

Also it should be noted that



Ȧǹ 



]

4 in Eq. (8.2.12) is the

pseudovector, which is a vector of a tensor, defined in Eqs. (2.3.9) and

(2.3.10) in Section 2, where

A is given from a consideration of the angu-

lar momentum equation and

]

is known as the vortex viscosity. It is fur-

ther noted that in Eq. (8.2.12), is the angular velocity of a fluid particle

with a rigid rotation defined by

uu ේ21

and

Ȧ is the average angular

velocity of a constituent particle. Giving the definition of

A , A will be

further discussed in the angular momentum equation.

The Maxwell stress tensor in the electromagnetic field, assuming that

the magnetic fluid is nonconductive, is proposed by Landau and Lifshitz

(1960)

HBIT 

emem

(8.2.13)

509

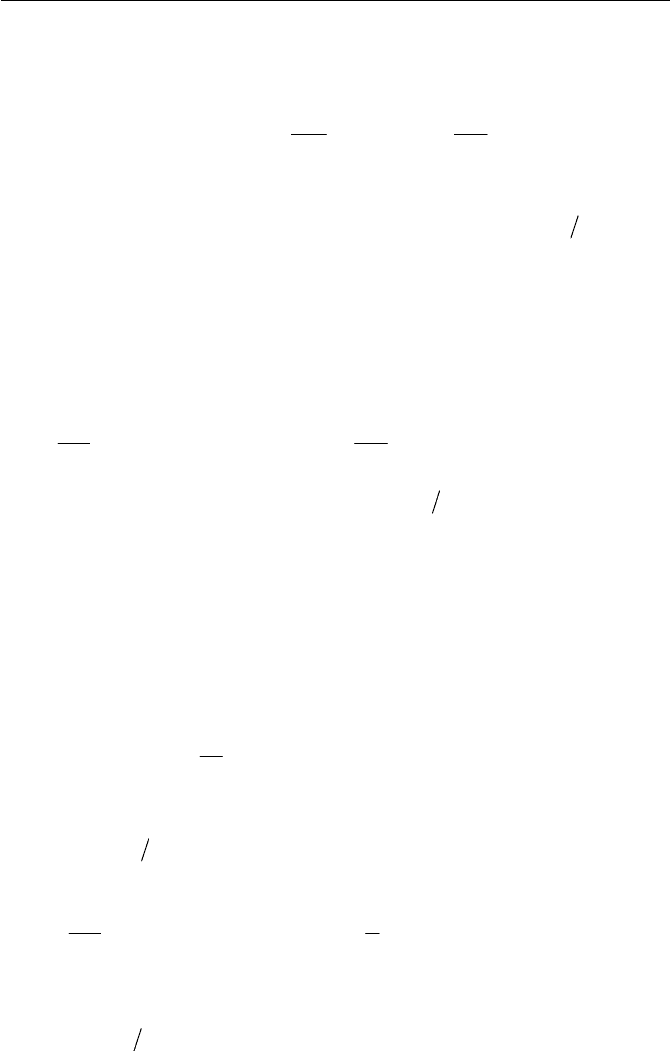
where

P is the electromagnetic energy per unit volume in a vacuum

space, which is understood as







(8.2.14)

For magnetic fluids with a Langevin magnetization as in Eq. (8.1.1),

proportional to

and resultantly

would be equal to



ww so

that the first term of Eq. (8.2.14), may vanish.

The substitution of Eq. (8.2.8) together with constitutive equations to

the Cauchy’s equation of motion given in Eq. (8.2.2), regarding magnetic

fluids as nonconductive, i.e.

0ේ u H , and with the continuation of mag-

netic induction

B , i.e. 0ේ  B , we can derive the linear momentum

equation as follows



u ȦHMu

(8.2.15)

where

p is the total pressure, 2

Hpp



and

is the rotational

relaxation time of particles due to the vortex viscosity. It will prove useful

to consider here, as another point of correspondence that will be discussed

to a larger extent in the angular momentum treatment, to write Eq. (8.2.15)

with the field parameters of M and H , eliminating the parameter

Ȧ of a

microscopic concept.

From the angular momentum equation of magnetic fluids, if one as-

sumes that

is sufficiently small and the spin diffusion is ignored, it is

reasonable to minute its relationship from Eq. (8.2.25), where



HMȦ u 

(8.2.16)

It is noted that A given where



ȦA ᧩᧩

]

4 is replaced by the rela-

tionship

]

22 . Thus, the substitution of Eq. (8.2.16)–(8.2.15) yields

the linear momentum equation of magnetic fluids, that is written as



gHMHMu

UKU

uu

(8.2.17)

Equation (8.2.17) includes the term HM

ේ , which is the so-called the

Kelvin force density, derived from the stress of an electromagnetic field,

and the term



HM uuේ21 , which is derived from the consideration of

8 Magnetic Fluid and Flow

510

8.2 Ferrohydrodynamic Equations

an internal angular momentum to give the skew-symmetric part of the

viscous stress tensor.

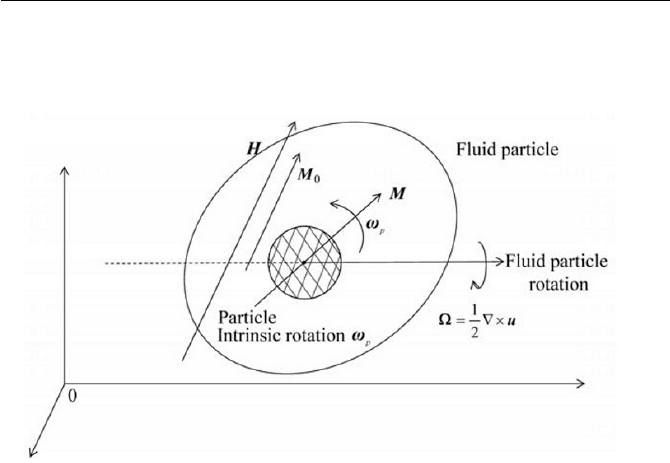
Fig. 8.4 Intrinsic rotation of magnetic particle against rotation of fluid

particle

In order to derive the angular momentum equation of a magnetic fluid,

it is useful to give a visual image of the intrinsic rotation of a magnetic

particle as schematically represented in Fig. 8.4. We will consider that the

magnetic moment of the particle is fixed within the particle, assuming that

the magnetization relaxation occurs by means of the Brownian relaxation,

as discussed earlier. The situation sketched in Fig. 8.4 is that a magnetic

field H is applied to the suspension under a shear flow, where the rotation

of fluid particles is given in . The applied magnetic field will then try to

align the magnetic moment m (where

; V

for the volume

element of a magnetic body) with the same direction of H , while the vis-

cous torque exerted by the flow tries to rotate the fluid particle with .

Thus the direction of m (or M ) will be misaligned with the direction of

H , since the moment is fixed in the particle. This misalignment with M

and H gives rise to a magnetic torque that tries to realign the magnetic

moment, which counteracts the viscous torque. The particle will then rotate

to a frame of reference with the angular velocity of

Ȧ , which is different

from the rotation of the fluid particle, as indicated in Fig. 8.4. Thus, the

particle rotates internally in the fluid particle with the torque counteracting

511

the free rotation of the particle, and resultantly this torque gives rise to an

increase of the fluid’s viscosity.

In this case, however, when the magnetic field H is applied as colin-

ear with the rotation of the fluid particle, the magnetic moment m (or

M ) will be aligned with the same direction of H ( M // H ), and with that

there is not any field influence, rotating the particle with the same angular

velocity (

Ȧ = ). Obviously, when there is no magnetic field

0 H

the particle has no preferable direction to be oriented, and rotates freely

with the same angular velocity of the fluid particle. The theoretical expla-

nation of magnetoviscous effect in diluted magnetic fluids was given by

Shliomis (1972); this also gives the basis for the development of ferrohy-

drodynamic equations.

By considering the establishment of the angular momentum equation

of magnetic fluid, we can write Eq. (8.2.3), using the stress tensor given in

Eq. (8.2.9), as follows

İc

 ේ





(8.2.18)

Here, it is mentioned that

is replaced by the intrinsic angular momentum

of the particles with the particles rotation

Ȧ , as

IȦs

. Denote that the

explicit expression of f

in Eq. (8.2.3) is disregarded here at this point.

The constitutive equation for the couple stress tensor or the surface

couple stress tensor

is difficult to obtain, but it is simply assumed that

is symmetric and diffusive by the intrinsic rotation

(the angular spin

rate) analogous to the Newtonian viscous fluid, which is dependent upon

the rate of strain, Rosensweig (1985), as follows







ppp

ȦȦȦ ේේේ  'Ic

(8.2.19)

where, by analogy,

and

are respectively called the shear and bulk

coefficients of the spin viscosity.

The terms,

İ :



T and İ :

T , that appear in Eq. (8.2.18) are treated

with the following considerations. Firstly, we can consider the origin of



T that is derived from an extraneous magnetic torque to maintain

against under magnetic field, Rosensweig (1988)



Ȧ 

Tİ

(8.2.20)





Ȧ 

]

(8.2.21)

: :

8 Magnetic Fluid and Flow 512

8.2 Ferrohydrodynamic Equations

is replaced by the vortex viscosity

]

with the relationship

]

I .

It is noted that Eq. (8.2.21) gives the definition to the pseudovector

A as it

appears in Eq. (8.2.12), so that, as a result





ȦA 

]

(8.2.22)

As for the second variant

T , we can calculate the tensor product

by substituting the Maxwell stress tensor given in Eq. (8.2.13) together

with the polarization relationship given in Eq. (8.2.7) to yield

İ :

HM u

(8.2.23)

Therefore, after giving the constitutive relationships discussed above,

substituting the expressions from Eqs. (8.2.19), (8.2.21) and (8.2.23), into

Eq. (8.2.18), we can obtain the angular momentum equation of a magnetic

fluid by writing:

 

HMȦȦȦ

u





KKO

(8.2.24)

It has been mentioned that

HM u that appears in Eq. (8.2.24) is equiva-

lent to the body couple

in Eq. (8.2.3), which is the torque density

(torque per unit volume).

In a case when

is sufficiently small and the diffusion and convection

of the particle rotation

are regarded as minimal, we can write Eq.

(8.2.24) in a further simplified form where



HMȦ u 

(8.2.25)

Note that

101606



for

10|d

nm,



smkg  and

mkg106u

, where

is a particle material density.

The energy equation given in Eq. (8.2.4) is constituted by giving

and

c , where

q may be straightforwardly constituted by the Fourier’s law of

Eq. (2.5.28) and c is given in Eq. (8.2.19). However, at this stage it is ap-

propriate to reduce the equation to the most widely used (or rather practi-

cal) expression under assumptions that: the magnetic fluid is (electrically)

nonconductive disregarding intrinsic rotation; the magnetization is linear

in terms of

and

; it is incompressible with constant coefficients; and

neglects all heat sources due to magnetoviscous and viscous effects and in-

ternal heat generation. The resultant equation is written in the following

expression where

513







(8.2.26)

In Eq. (8.2.26) the second term at the left hand side represents the magne-

tocaloric effect, where the magnetocaloric effect is associated with the

change of magnetic field intensity with time at

tH ww and the fluid travel-

ing through the magnetic field

Hu  . However, for a small dependence

of magnetization

on temperature change, i.e.





0|ww

TM (except

for a temperature sensitive magnetic fluid, which has a large temperature

dependence on magnetization), Eq. (8.2.26) can be reduced to the conven-

tional temperature field equation as follows



(8.2.27)

Probably the most characteristic treatment in deriving ferrohydrody-

namic equations is that the instantaneous magnetization

M of the suspen-

sion is different from the equilibrium magnetization

M , which is given

for a diluted suspension from the Langevin magnetization formula of Eq.

(8.1.1). In addition, as described in association with Fig. 8.4, the relaxation

M is coupled with a dynamic change of the flow field. Shliomis (1972,

also reviewed article 2002), obtains a phenomenological expression of the

magnetization of magnetic fluids, transferring the Debye relaxation equa-

tion (1929) of a rotating (local) frame of reference, which rotates with a

magnetic particle

Ȧ , to the fixed (laboratory) system in the following

manner.

The Debye-like magnetization equation in the rotating frame of refer-

ence is given as





(8.2.28)

The rates of change of any vector, say in our case

,M in the rotating frame

of reference to the fixed system can be expressed by the relationship

MȦ

u

(8.2.29)

Combing Eq. (8.2.28) and (8.2.29), we have



MMMȦ

u

(8.2.30)

8 Magnetic Fluid and Flow 514