Yamaguchi H. Engineering Fluid Mechanics (Fluid Mechanics and Its Applications)

Подождите немного. Документ загружается.

8.3 Basic Flows and Applications

a magnetic body force seems to be one of the most attractive effects in

magnetic fluid statistics. Since the appearance of magnetic fluids, the prin-

cipal application of magnetic fluids is largely found in rotary shaft seals, as

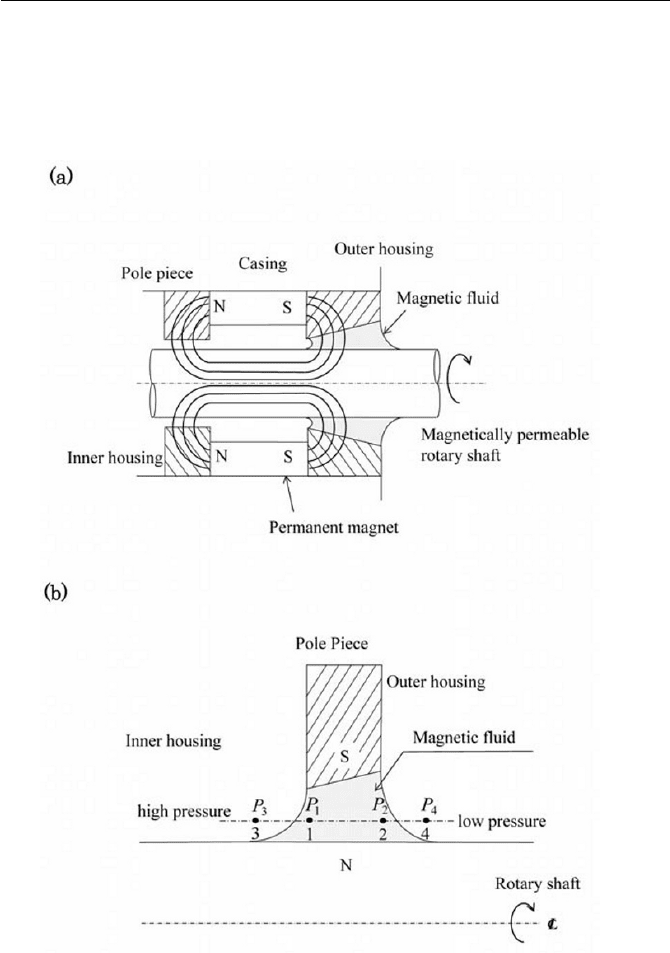
displayed schematically in Fig. 8.8. As seen in Fig. 8.8(a), a small volume

of a magnetic fluid is sustained in the annular region between a rotating

shaft and a surrounding cylindrical magnetic pole, where the magnetic

fluid maintains direct contact with both shaft and pole piece, providing a

virtually leak-proof liquid seal. The pressure difference between the inner

and outer housing, say

p (high pressure side ) and

p (low pressure side )

with reference to Fig. 8.8(b), can be maintained under a rotating shaft con-

dition. The pressure difference

ppp  ' , i.e. the seal pressure, can be

estimated by the static equilibrium equation in Eq. (8.3.6), assuming that

the gravitational force is ignored and the magnetic fluid in the gap is in a

static state with a condition of the magnetic field to be tangential at the in-

terface, i.e. 0

M . With the magnetic condition at the interface, there

would not be a magnetic pressure jump, so that

and

Thus, at first approximation, the pressure difference

p can be estimated

2143

dHHMppppp ')'(

᧩᧩

(8.3.14)

The integral in Eq. (8.3.14) depends on the magnetization law. In a weak

magnetic field, i.e.

, so that the integral is given where

³³

HHdHHdHHM )(''')'( ᧩

(8.3.15)

In a case of strong magnetic fields,

MHM )( , and the integral is of the

form

  

HHMdHHM ᧩''

(8.3.16)

where

is the equilibrium saturation magnetization given in Eq. (8.1.2).

In a general case, the Langevin formula given in Eq. (8.1.1) can be

used to calculate the integral, which is found to give



sinhln

TNkdHHM

]]

᧩

')'(

(8.3.17)

The magnetic fluid seals are in commercial use as pressure-, vacuum-

and dust-seals employed in both rotary and reciprocating shafts. As veri-

fied in the text above, the main characteristic ensuring the seal perform-

ance is the magnetic field strength in a gap space. In more technical views,

525

care must be taken to choose the most appropriate type of magnetic fluid

to prevent deterioration or evaporation of carrier liquids, depending upon

the combination of the contact fluids.

Fig. 8.8 Rotating shaft magnetic fluid seal

8 Magnetic Fluid and Flow

526

8.3 Basic Flows and Applications

8.3.3 Thermoconvective Phenomena

The Kelvin force density

ේ

that appeared in the Rosensweig equation

is an additional body force term for the gravitational body force (if the

fluid motion under the gravity field is considered). The term

ේ , as

seen in the previous section, plays an important part in determining the

flow behavior of magnetic fluids. Let us now consider, if a temperature

field



is introduced into the flow field of internal flows, a situation of

a thermomagnetic natural convection that is analogous to a thermal gravi-

tational natural convection.

The problems found in determining the thermomagnetic natural con-

vection are similar to what was considered in the thermal gravitational

natural convection in the way that the onset of a natural convection is

caused by a hydrodynamic instability that breaks the mechanical equilib-

rium of fluid at a hydrodynamically static state, Landau and Lifshitz

(1959) and Gershuni and Zhukhvitskii (1976). In this section, for the sake

of clarity the simplest case of the natural convection, the so-called Benard

convection, is considered as schematically represented in Fig. 8.9. As

shown in Fig. 8.9(a) and (b), the thermal configuration is such that two

dimensional infinite solid horizontal layers are arranged in parallel, in

which the temperature of the interface of the bottom layer is set higher

than that of the upper layer. Between the two layers a magnetic fluid is

charged, where the density

and magnetization

of the magnetic fluid

posses a spatial non-uniformity due to a temperature distribution. It is as-

sumed that the two solid layers have an infinite magnetic permeability and

a thermal conductivity.

At the beginning, the state of the fluid is at a quiescent state of me-

chanical equilibrium 0

u , where an externally applied magnetic fluid H

and temperature difference

TTT 

are very small, and the heat is

transferred from the bottom wall to the upper wall by the thermal conduc-

tion through the magnetic fluid layer, as indicated in Fig. 8.9(a). This is the

conduction state, where isothermal temperature distribution persists. As

thermal and/or magnetic conditions are changed, as we will discuss here,

there should be a threshold condition, upon which a natural convection

mode appears, followed with the appearance of cellar structure of flow,

known as the Benard cell as schematically shown in Fig. 8.9(b). With this

mode of flow, i.e. at the state of a natural convection, the heat transfer rate

increases drastically compared to the thermal conduction state due to a

convective motion of flow.

527

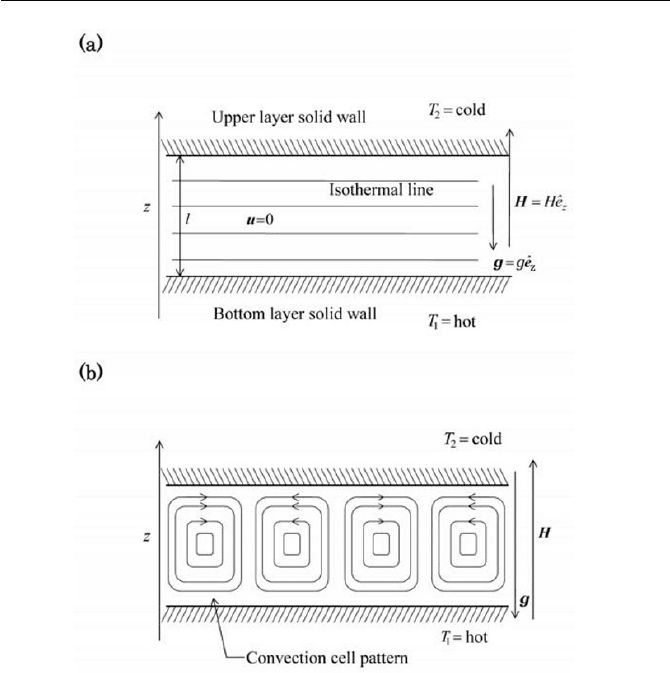
Fig. 8.9 Problem of Benard convection in thermomagnetic natural con-

vection

In order to develop knowledge in critical phenomena at the occurrence

of a thermomagnetic natural convection, we will examine the mechanism

by firstly writing conditions for a mechanical equilibrium. The requisite

mechanical equilibrium is given by taking the rotation of the Rosensweig

equation at the hydrodynamically static state 0

u , as follows

uu HMg

(8.3.18)

In examining appropriateness of Eq. (8.3.18), we shall assume here

that the temperature dependence for the properties of



and

8 Magnetic Fluid and Flow 528

8.3 Basic Flows and Applications



HTMM ,

, where

varies in position

likewise



zTT

, so that we

have



and







(8.3.19)

It is further mentioned that the magnetic fluid is assumed to be homo-

geneous in terms of the concentration of a magnetic phase in a fluid. The

substitution of Eq. (8.3.18) to Eq. (8.3.19) yields the necessary condition

of a mechanical equilibrium, that is

0ේේ u





(8.3.20)

The existence of the critical phenomena, namely the transition to a

flow of natural convection from the state of thermal conduction requires

the parallelity of

T

to g and

H

. At a condition when this parallelity

is broken, the equilibrium (the static) state would not be possible, at which

moment the onset of a convection motion,

0zu

, appears.

Thermal characteristics found in problems of the Benard convection

are solely determined by the Rayleigh number

Ra as discussed in Exer-

cise 6.2.1, which is defined as

lcT

PrGrRa

ේg

(8.3.21)

The temperature gradient

T is defined by lT ,

c is the specific heat,

k is the thermal conductivity,

is the kinematic viscosity. Note that

is the coefficient of thermal expansion that is defined as

^`

1 TT



(8.3.22)

It is further mentioned that

and

T are a reference density and tempera-

ture respectively. All thermophysical values are bulk values of a magnetic

fluid.

Some simplifications are expressed by assuming a linear magnetization

relationship, a so-called soft magnet approximation to the magnetic fluid.

By the use of that from Eq. (8.1.3), the magnetization can be written

analogously to Eq. (8.3.22),

^`

1 TTMM



(8.3.23)

529

where

is defined as the relative pyromagnetic coefficient.

Satisfying the condition of parallelity given in Eq. (8.3.20), i.e.

H//g , with the critical phenomena of the natural convection of a mag-

netic fluid, the Rayleigh number defined in Eq. (8.3.21) can be modified to

write

XEEU

cpmT

klc

))((

 g

(8.3.24)

The important consequence of deriving the expression found in Eq.

(8.3.24) is that the flow instability at the onset of a natural convection is

adequately described by the known solutions of ordinary thermoconvective

stability problems, by adding an extra term of thermomagnetic force action

to the buoyant force effect.

Taking into account of the magnetic polarization relation expressed in

Eq. (8.2.7), the magnetic field gradient

dzdH can be rewritten by the fol-

lowing sequence

ȂH  

(8.3.25)

Equation (8.3.19) has a scalar component for

where

MH  







 H

(8.3.25)

so that







(8.3.26)

where the field gradient is given as



(8.3.27)

Therefore,

in Eq. (8.3.24) can be decomposed into two basic terms as

substitute Eq. (8.3.27) for Eq. (8.3.24), yielding

8 Magnetic Fluid and Flow 530

8.3 Basic Flows and Applications



dTM





XFP

(8.3.28)

The first term

aR is an ordinary (thermogravitational Rayleigh number)

and the second term

mR is defined as the magnetic Rayleigh number. An

important result obtained from Eq. (8.3.28) is that the

mR in all directions

dzdTT  is positive, indicating that in the irrespective of the direc-

tion of the magnetic field gradient

dzdHH  the temperature perturba-

tion of the magnetizing field always leads to the thermoconvective fluid

destabilization.

In determining the critical Rayleigh number

R at the first transition

of the Benard convection, the Rayleigh number at the onset of first appear-

ance of the Benard convection cells, Gotoh and Yamada (1982), show that

(detailed by numerical study) the parameter





000

HBK , the

characteristic parameter of the nonlinearity of the fluid magnetization

curve, plays an important role, and further show that in cases where

foK

(sufficiently large K ), the stability problem will become a con-

ventional stability problem of a Benard convection, as derived in Eq.

(8.3.28). Consequently the critical Rayleigh number 1708

R is found

to be applied for ordinary thermogravitational and thermomagnetic terms,

which are written as

1708

ccc

 maa RRR

(8.3.29)

The results obtained from a series of numerical work are also formulated

by a linear relation



(8.3.30)

where

R is the critical magnetic Rayleigh number in the absence of the

gravitational effect, as

foK , Blums et al. (1997).

The experimental evidence, Schwab et al. (1983), also supports the re-

lationships found in Eqs. (8.3.24) and (8.3.28), as schematically shown in

Fig. 8.10, where

Nu is the Nusselt number (with reference to Fig. 6.2 for

an ordinary natural convection). As seen in Fig. 8.10, the increase of the

magnetic field

results in a lowering of the critical Rayleigh number,

destabilizing the fluid state, and resultantly enhancing the heat transfer rate

as thermal mixing increases by the convecting motion of the fluid.

531

The compatibility between g

and

ේ is interesting, particularly

in application to space engineering, where in the non-gravity condition a

body force may be altered or controlled by means of

ේ . Widespread

engineering applications or pure fluid science problems are found in space

environments in conjunction with thermoconvective phenomena.

Fig. 8.10 Heat transfer characteristics in thermomagnetic

convection

(replotted after Schwab et al., 1983)

Exercise

Exercise 8.3.1 Magnetic Field Boundary Conditions

Give boundary conditions for a magnetic field when two magnetically

permeable media are in contact, one of which is a magnetic fluid. Consider,

taking account of the magnetic field boundary conditions, the pressure

jump at the interface of a stationary media.

Ans.

The two magnetic field conditions given in Eqs. (8.2.38) and (8.2.39)

can be applied to the boundary of magnetic fluids and magnetically perme-

able media. For the induction of

B , firstly according to the Gauss’s diver-

gence theorem, we can write the following relationship as

8 Magnetic Fluid and Flow

and Pressure Jump

532

Exercise

0)(

2n ln

 

³³

dSBB

SBB

(1)

Equation (1) yields the result that

0)( or

212n1

 nBB

(2)

It is mentioned that

is the normal vector directed to medium 2 (suppos-

ing magnetically permeable medium) from medium 1 (supposing the mag-

netic fluid), as indicated in Fig. 8.11.

Equation (2) shows the continuity of the normal induction

B , when B

passes through the interface of the media with different magnetization

2nn

MM and

. Equation (2) also gives a jump to the normal magnetic field

intensity

H , which is equal to the difference of a normal fluid magnetiza-

tion

, so that



nnnn

MMHH

1221

 

(3)

For the magnetic field

H , according to the Ampere’s circulation law,

we can write the relationship at the interface

0dlHHdd

  u

³³

)( ) ේ(

lHSH

(4)

Equation (4) yields the result that

0)( or

2121

u nHH

(5)

Fig. 8.11 Refraction at an interface

533

The conditions given in Eq. (5) involve the continuity of the tangential

magnetic field intensity

H at the interface. Altogether, Eqs. (2) and (5),

give the conjugation of a magnetic field at an interface for an induction

and magnetic field intensity. This conjugation gives an insight into the so-

lution for a magnetic field at a boundary, such as a consideration of the re-

fraction of magnetic flux lines of

B and

B at the interface of two media,

as shown in Fig. 8.11. Denote that

is the angle between the magnetic

flux line and the tangent to the interface, so that

tan BB

, consider-

ing

for each medium at the interface, we may obtain the follow-

ing relationship

tan

(6)

where

and

are the magnetic permeability of medium 1 and medium

2 respectively. For example, as shown Fig. 8.11, in the case of

 , the

magnetic flux line of medium 2 has a high refraction angle at the interface.

Now consider dynamic boundary conditions at the interface, simply as-

suming that the two media are thermally at equilibrium, i.e. isothermal and

stationary, i.e.

0 u

at the interface. The stress tensor for a magnetic fluid

can be written as, according to Eqs. (8.2.9) and (8.2.13)

HBIT  )

(

(7)

With the allowance of the conjugation of a magnetic field at an inter-

face, the normal stress difference at the interface is balanced at the station-

ary condition so that





nnMnMnn

nnnn

ˆˆˆˆˆ

BHBH

ˆˆˆ

1122

10020112

111









 

HHpp

(8)

where the third term in the right hand side of equation is due to the surface

tension where

is the coefficient of the surface tension and

R and

are the main surface curvature radii. With 0

 nn

T , we can obtain

8 Magnetic Fluid and Flow 534