Yi Lin. General Systems Theory: A Mathematical Approach

Подождите немного. Документ загружается.

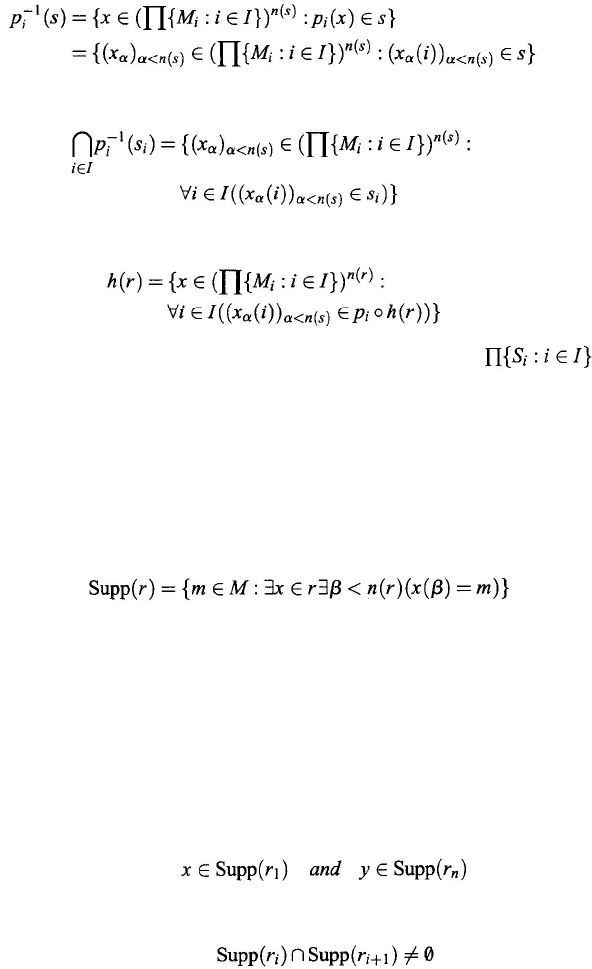
214

Chapter 9

and for each i ∈ I and s ∈ R

(9.66)

Equation (9.66) implies that for every s

∈ R

with n

(

) =

(

(9.67)

So Eq. (9.65) implies that

(9.68)

This implies that the relation

(

) belongs to the relation set of



9.4. Structures of Systems

Let S = (

M,R

) be a system and r ∈ R a relation. The support of r, denoted

Supp(

), is defined by

(9.69)

⊕ S

, where

The system S is connected if it cannot be represented in the form S

and

are nontrivial subsystems of

Theorem 9.4.1. For every system S = (M, R) the following conditions are equiv-

alent:

(i) The system S is connected.

(ii) For any two objects x and y

∈ M, there exist a natural number n > 0 and n

relations r

∈ R such that

(9.70)

and

(9.7 1)

for each i = 1,2, . . . , n – 1.

General Systems: A Multirelation Approach

215

Proof: (i) → (ii). We prove by contradiction. Suppose that the system S is

connected and there exist two objects x and y

∈ M such that there do not exist

relations r

∈ R, i = 1,2,. . . , n,

for any natural number

≥

1, such that

(9.72)

and

(9.73)

for each i = 1,2, . . . ,

–

1. From the hypothesis that S is connected, it follows

that there must be relations r

∈ R such that x ∈ Supp(r

) and y ∈ Supp (

Then our hypothesis implies that

(9.74)

Let

and for each natural number n ∈

let

(9.75)

and

(9.76)

Then

and

for

all natural numbers

n, m

∈

We now define two subsystems

of S such that

(9.77)

(9.78)

(9.79)

(9.80)

Then

and

In fact, for each relation r ∈ R, if r ∉ R

and so

thus r ∈ R

Therefore,

contradiction.

(ii) → (i). The proof is again by contradiction. Suppose condition (ii) holds

and

is disconnected. Thus, there exist nontrivial subsystems

and S

of S such

that S = S

⊕

. Suppose that

Pick an object m

∈ M

216

i = 1,2. Then there are no relations r

∈ R, j = 1, 2, …,n, for any fixed n ∈

such that

and

for each j = 1,2, … , n

–

1, contradiction.

Chapter 9

(9.81)

(9.82)



Let

⊆ M , where S = (M, R

)

is a system. Define the star neighborhood of

the subset

, denoted Star (

), as follows:

By applying induction on

∈

we can define

Star

(

) = Star(

)

and

(9.83)

(9.84)

Star

) = Star(Star

(

))

(9.85)

Corollary 9.4.1. For every system S =

(

M, R

)

the following conditions are equiv-

alent:

(i) The system S is connected.

(ii) For each object x

∈ M, Star

Proof:

(i)

→ →

(ii) follows from Theorem 9.4.1 directly.

(ii)

→

(i).

or any two objects x, y ∈ M

, from the hypothesis that Star

∞

({p})=

, for every object p ∈ M, it follows that there exist n, m ∈ and relations

∈

such that

(9.86)

(9.87)

and

Thus, it follows that Theorem 9.4.1(ii) holds and from Theorem 9.4.1 that S is

connected.



An object m in a system

is isolated if there is not relation r

∈ R

such that the cardinality

and

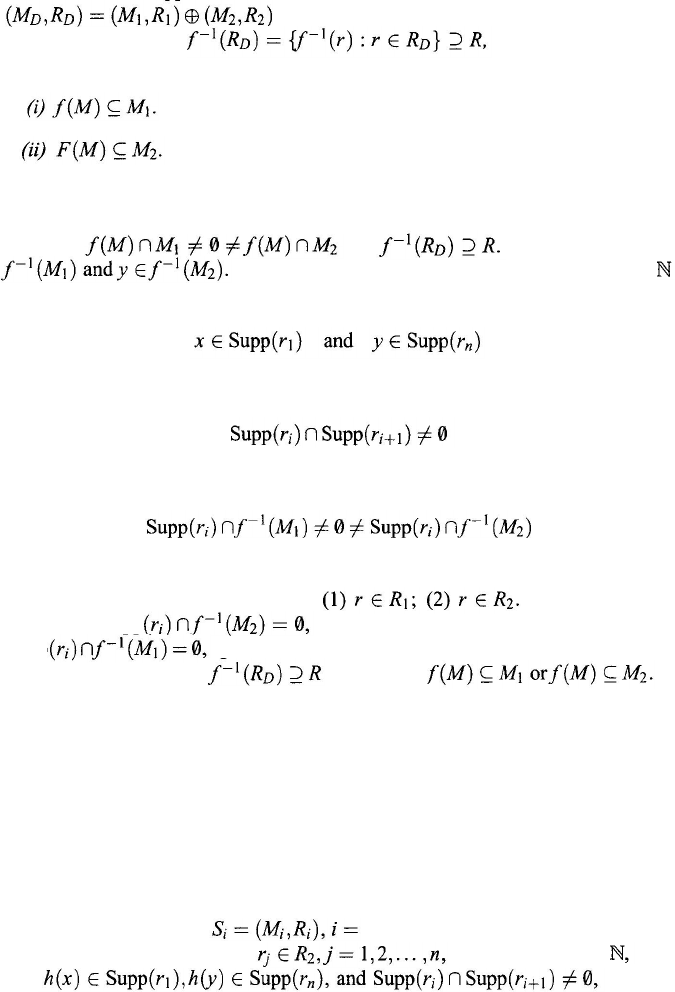
General Systems: A Multirelation Approach

217

Corollary 9.4.2. There is no isolated object in a connected system.

Theorem 9.4.2. Suppose that S = (M, R

)

is a connected system and D =

is a disconnected system. If there exists a map-

ping f : S

→ D with then only one of the

following holds:

Proof: We prove by contradiction. Suppose there exists a mapping f : S → D

such that

and

Pick elements x ∈

From Theorem 9.4.1 it follows that there exist n ∈

and

relations r

∈ R, i = 1, 2, …, n,

such that

(9.88)

and

(9.89)

for each i = 1, 2, … , n – 1. Pick an i with 1≤ i ≤ n

such that

(9.90)

Sinceƒ

–1

) ⊇ R, it follows that there exists a relation r ∈ R

such that

ƒ(r

) =

r. Now there are two possibilities: If (1) holds, we

must have Supp

contradiction.

If (2) holds, we will have

Supp

again a contradiction. The contradictions imply that every

mapping f : S → D with

must satisfy



Corollary 9.4.3. Let h : S

→ S

be a homomorphism from a connected system S

into a system S

Then h

) = (

(

), h

(

))

must be a connected partial system

of S

Theorem 9.4.3. Suppose that h : S

→ S

is an S-continuous mapping from a

system S

into a system S

If S

is connected, the S is also.

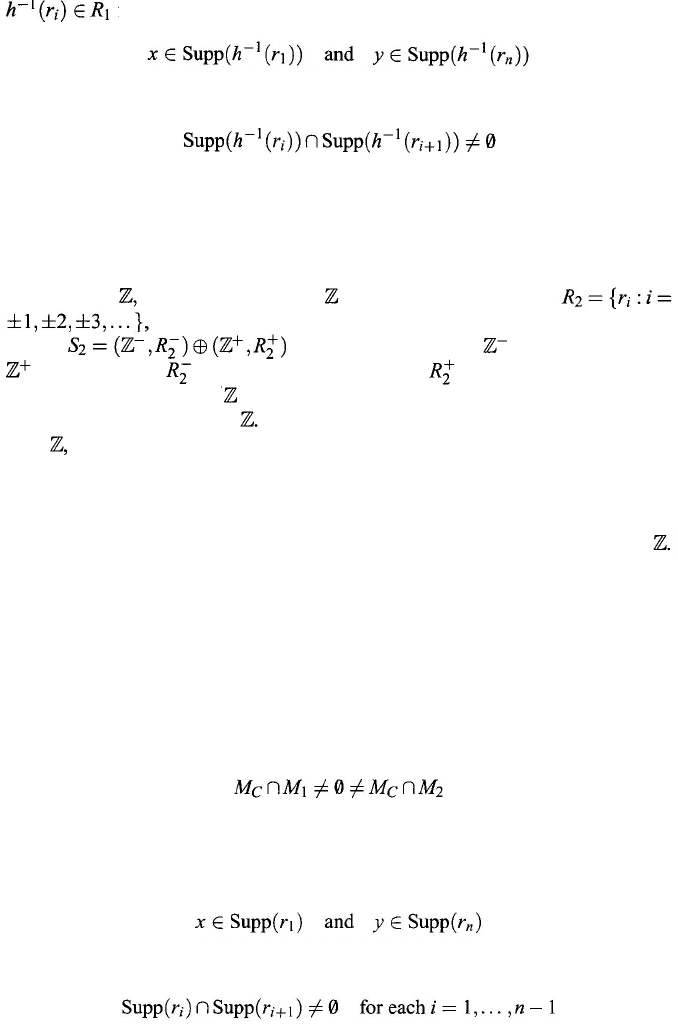
Proof: Suppose that

1, 2.

Let us pick two arbitrary objects

x, y

∈ M

There are relations

for some fixed

∈

such

that

for each

218

Chapter 9

i = 1, 2, … , n – 1. From the hypothesis that h is S -continuous, it follows that

for

= 1, 2, … ,

Thus,

(9.91)

and

(9.92)

for i = 1, 2, … , n – 1. From Theorem 9.4.1 it follows that S

is connected.



Example 9.4.1. We construct an example to show that the connectedness of the

system

cannot guarantee the connectedness of the system

in Theorem 9.4.3.

Let

= (

) be a system where is the set of all integers and

where for each i = ±1, ±2, ±3, … , r

= {(i,i+1)}.Then the

system

is disconnected, where

= {0, –1, –2, … },

= {1, 2, 3, … },

= {

: i = –1, –2, …} and = {r

= 1, 2, . . .}.

Define a system S

= ( ,

) as follows: R

= {r

: i = 0, ±1, ±2, … }, where

= {(

i, i

+ 1)}

or each i

∈ Then S

is connected. In fact, for any two objects

i,j

∈

there exist relations

r , … , r, where we assumed that i < j, such that

i+l

i ∈ Supp(

i, i + 1}, j ∈ Supp(

) = {

) = {j,j + 1}, and Supp(

)

∩

Supp(

) =

k+1

{

k + 1}, for k = i, i + 1, . . . ,j –

1. Therefore, it follows from Theorem 9.4.1 that

is connected.

Let h : S

→ S

be the identity mapping defined by

(i) = i for each i ∈

Then h is S

-continuous, and

is connected, and S

is disconnected.

Theorem 9.4.4. If a subsystem C of a system S is connected, and for every pair

, S of subsystems of S with disjoint object sets such that C is a subsystem of

⊕ S

then C is a subsystem of S

or S

Proof:

We show the result by contradiction. Suppose that

is not a subsystem

nor of S

. Let C = (

)

and S

= (

= 1,2. Then

(9.93)

Pick elements x ∈ M

∩

and y ∈ M

∩

Since C is connected and from

Theorem 9.4.1, it follows that there exist a natural number n > 0 and n relations

∈ R

, for

= 1, 2, … ,

, such that

(9.94)

and

(9.95)

General Systems: A Multirelation Approach

219

Therefore, there must be an i satisfying 0 < i ≤ n such that

(9.96)

From the definition of subsystems it follows that there exists a relation r in the

free sum

such that

It follows from the definition of free sums

that r is contained either in R

or in R

, but not both.

Therefore, if r

∈ R

Supp(

)

∩

= Ø

; if r ∈ R

, Supp(

)

∩

= Ø

, contradiction. This implies that

is a subsystem of

or S



Theorem 9.4.5.

Let

{ C

= (M

, R

) : i ∈ I } be a set of connected subsystems

of a system S =(M,R). If there exists an index i

∈ I such that each sys-

tem

is connected, for each i ∈ I, then the system

is connected.

(9.97)

(9.98)

Proof: Let us pick two arbitrary objects x and y from There are two

indices i and j such that x

∈ M

and y ∈ M

. Choose an object z ∈ M

. From the

hypothesis that the systems

are connected, it follows that there are natural numbers n and m and relations r

and

∈ R, for k = 1,2, … , n and p = 1,2, … , m, such that

and

(9.99)

(9.100)

Therefore, Theorem 9.4.1 implies that the system is

connected.



Corollary 9.4.4. If the set {C

= (M

, R

) : i ∈ I} of connected subsystems of the

system S = (M, R) satisfies

then the subsystem

is connected.

Let S = (M, R) be a system and D ⊂ M a subset. The subset D is dense in the

object set M if the following conditions hold:

(i) For any relation r

∈ R with r ≠

, Supp(

)

∩

≠

Ø .

(ii) Each isolated object in M belongs to D.

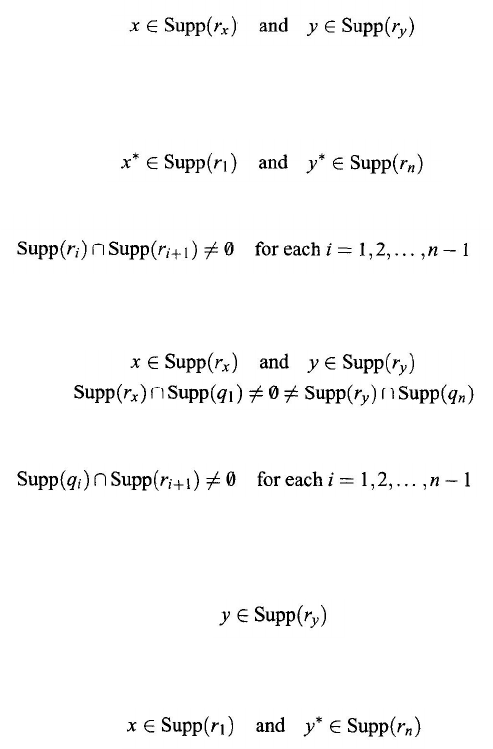
220

there are natural number n and n relations r

and

A subsystem S* = (M*,R*) of S is a dense subsystem of S if the object set M* is

dense in M.

Theorem 9.4.6. If a system S = (M,R ) contains a connected dense subsystem,

then S is connected.

Proof:

Suppose that S* = (M*,R*) is a connected dense subsystem of S. To

show that S is connected, we pick two arbitrary objects x, y

∈ M. There are three

possibilities: (1) x, y

∈ M – M*; (2) one of x and y is contained in M* and the

other is contained in M – M*; (3) x, y are contained in M*.

If possibility (1) holds, x and y are not isolated objects in M. Therefore, there

are relations r

and r

∈ R such that

(9.101)

It follows from the definition of dense subsets that there must be an object x* ∈

Supp(

) ∩ M* and an object y* ∈ Supp(

)

∩

M*.

Theorem 9.4.1 implies that

∈

R*, i

= 1, 2, . . . ,

such that

(9.102)

(9.103)

For each

= 1, 2, . . .

, n, let q

be a relation in R such that r

⊂

⏐

M*. Then it has

to be that

(9.104)

(9.105)

and

(9.106)

Theorem 9.4.1 implies that S is connected.

If possibility (2) holds, without confusion, let x

∈ M* and y ∈ M – M*. Then

y is not an isolated object in M. Let r

∈ R be a relation such that

(9.107)

Pick

∈

Supp(

)

∩

M*.

From the hypothesis that

is connected, it follows that

there are a natural number n > 0 and n relations r

∈

R*, i

= 1, 2, . . . ,

such that

(9.108)

Chapter 9

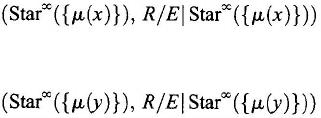
General Systems: A Multirelation Approach

221

and

Supp(

)

∩

Supp

(

i +1

) ≠

for each i = 1, 2, . . . , n–1

(9.109)

For each

= 1, 2, . . . ,

let

be a relation in

such that

⊂ q

⏐

. Then

x ∈ Supp(

) and y ∈ Supp(r

)

Supp (

)

∩

Supp (

i +l

) ≠ Ø for each i = 1,2, . . . n – 1

(9.110)

(9.111)

and

Supp(

)

∩

Supp (

)

≠

(9.112)

Applying Theorem 9.4.1 we have showed that S is connected.



A connected subsystem S

of S is maximal in S if there is not connected

subsystem

of S such that S

is a subsystem of S

and S

≠ S

. Each maximal

connected subsystem of S is called a component. Then, for each object m ∈ M,

the partial system (Star

∞

({

}),

⏐

Star

∞

({

})) of

is a component.

Theorem 9.4.7. Suppose that S = (M, R) is a system and E an equivalence re-

lation on the object set M. Then the quotient system S/E = (M/E, R/E) is

connected iff for any two components X = (

, R

) and Y = (

, R

) of S, there

exist a natural number n and n components S

= (

) of S, i = 1, 2, . . . , n,

such that there exist x

∈ M

∈

and m

, m

∈ M

, i =

1, 2, .

. . , n, satisfying

(x,m

) ∈ E, (

)

∈

E, i

= 1, 2, . . .

, n

– 1,

and

(

)

∈

Proof: Necessity. Suppose that the quotient system S/E = (M/E, R/E) is

connected, and there exist two components X = (

, R

) and Y = (

, R

) of S

such that there do not exist components

= (

, R

) of

S, i

= 1, 2, . . . ,

for each

natural number

such that there exist

∈

and y ∈ M

and

, m

∈

for

each

satisfying (

x,m

) ∈ E, (

)

∈

E, i

= 1, 2, . . .

, n

– 1, and (

,y) ∈

Pick objects x

∈ M

and y ∈ M

We then make a claim.

Claim. The subsystems

and

of the quotient system S/E are not identical, where

µ : M → M/E is the canonical

mapping.

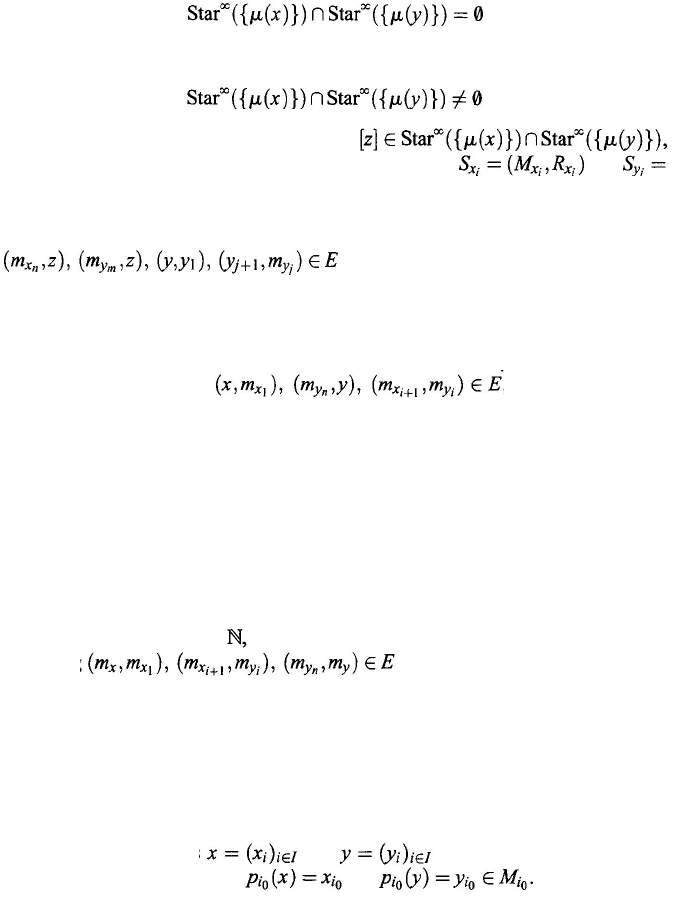
222

Chapter 9

This claim implies that the quotient system S

E is not connected. In fact,

from the hypothesis that the quotient system S

E is connected, it follows that for

each object

(

) ∈ M

E, the connected component of S

E containing the object

(

) must equal the whole system S/E.

We now see the proof of Claim 1. It suffices to show that Star

∞

({µ (

)})

≠

Star

∞

( {

(

)}). To this end, it suffices to show that

(9.113)

which we do by contradiction. Suppose that

(9.114)

for some

∈

and some

∈

. Choose

where

is an object in

Then there exist components

and

(

, z), for i = 1, 2, . . . , n and j = 1, 2, . . . , m, for some natural numbers n and

such that there are objects

∈ M

and

∈ M

, for each

= 1, 2, . . . ,

and j

= 1, 2, . . .

, m,

such that (

x, x

), (x

, m

) ∈ E, for i = 1, 2, . . . , n – 1, and

, for

= 1, 2, . . .

, m –

1. This contradicts

the assumption in the first paragraph of the necessary part of the proof.

Sufficiency. Suppose that for any two components X = (M

) and Y =

(

) of S, there exist a natural number n and components S

= (M

) of S,

i =

1, 2, . . . ,

such that there exist

∈

, y ∈ M

, and

∈

, for each

i =

1, 2, . . . ,

satisfying

, i = 1, 2, . . . , n – 1.

To show that S/E is connected, it suffices to verify that, for each object x

∈ M,

Star

∞

({

(

x)}) = M/E

(9.115)

by Corollary 9.4.1.

It is clear that Star

∞

({

(

x)}) ⊂ M/E. Suppose M/E ≠ Star

∞

({µ

(

)}). We

can then pick an object [m] ∈ M/E – Star

∞

({

(

x)}), where m is an object in

M. This implies that there are two connected components X = (M

) and

Y = (M

), such that x ∈ M

and m ∈ M

and for any two objects m

∈

and m

∈ M

there do not exist connected components S

= (M

, R

) of S,

i =

1, 2, . . . ,

for any

∈

such that there exist m

∈ M

i =

1, 2, . . . ,

satisfying

= 1, 2, . . . ,

– 1, contradiction

which implies that M/E = Star

∞

({

(x )}).



Theorem 9.4.8.

Let

{

: i ∈ I} be a set of systems such that there exists an

∈ I such that the system S

is connected. Then the Cartesian product system

∏

{

: i ∈ I

}

is connected.

Proof: Pick objects

and

from the Cartesian product

system

∏

{

∈

}. Then and . From Theorem

General Systems: A Multirelation Approach

223

9.4.1 it follows that there are a natural number n > 0 and n relations r

∈ R

j = 1, 2, . . . , n, such that

and

(9.116)

(9.117)

Therefore, the relations satisfy

and

(9.119)

for each i = 1, 2, …,

–1. Applying Theorem 9.4.1 we have proved the theorem.



Theorem 9.4.9.

Let

{

: i ∈ I} be a set of systems such that the product ∏

{

∈ I} is connected. Then each factor system S

is connected.

Proof:

Pick two arbitrary objects

and y

from a system

for any fixed

∈

There then are two objects x and y in the product system such that p

(x) = x

and

(y) = y

. From the hypothesis that the product system is connected, it follows

that there are a natural number n > 0 and n relations r

from the product system,

= 1,2, . . . , n, such that

∈ Supp

)

and

∈

Supp(r

)

and

for each j = 1, 2, …, n–1. Then the relations p

) ∈ R

, j = 1, 2, . . . , n, satisfy

and

(9.121)

(9.122)

(9.120)

(9.123)

for each j = 1, 2, . . . , n–1. Theorem 9.4.1 implies that S

is connected.

