Закгейм А.Ю и др. Математическое моделирование химико-технологических процессов
Подождите немного. Документ загружается.


11
2. Желательно сформулировать, почему вы двигались к оптимуму таким пу-
тем и где бы вы стали искать оптимум после проведенного анализа, если бы про-
должили поиск, и т.д.
3. Укажите ограничения, накладываемые на выбираемые условия, с учетом
вида полученных кривых и окончательно сформулируйте рекомендации по выбо-
ру оптимального режима.
Вывод должен представлять собой краткое обобщение изложенного в обсу-
ждении результатов, но не являться повторением этого раздела.
Следующие четыре работы (2,3,4 и 5) представляют собой единый цикл.
Исходные данные, полученные в работе 2, используются при выполнении всех
работ цикла, работы 2 и 3 посвящены моделированию и расчету реакторов, в
работе 5 производится оптимизация реактора.
Лабораторная работа №2. Получение кинетических характери-
стик химической реакции на основе результатов эксперимента.
2.1. Объект исследования и эксперимент.
Цель работы такова. Сделав небольшое число опытов, получить исходные
данные и по ним рассчитать параметры уравнения Аррениуса для каждой из ста-
дий сложной реакции. Это позволит в дальнейшем моделировать протекание дан-
ной реакции при различных температурах. Уравнение Аррениуса связывает кон-
станту скорости реакции с температурой:
RT
E
a
ekk
−
=
0
(2.1)
где k
0
– предэкспоненциальный множитель (предэкспонента), E
a
– энергия акти-
вации, R – универсальная газовая постоянная.
Следует учесть следующие особенности изучаемой реакции. Все ее стадии –
первого порядка, вне зависимости от стехиометрии стадий (это принято для уп-
рощения расчета и анализа объекта и практически не влияет на смысл данного
цикла работ). Для простоты расчета принимается, что реакция в работе 2 прово-
дится в аппарате идеального смешения. Это следует учитывать при вводе исход-
ной информации – числа ступеней (ячеек) ячеечной модели, на которую рассчи-
тана программа.
Для проведения численного эксперимента задаются температура и среднее
время пребывания в реакторе, результатом эксперимента являются концентрации
всех веществ на выходе из реактора. Вы должны задать условия таким образом,
чтобы по результатам эксперимента определить значения энергий активации и
12
предэкспоненциального множителя для каждой стадии реакции. Для этого нужно
провести серию опытов при разных температурах. Для расчета энергии активации
и предэкспоненты по уравнению Аррениуса минимальный объём серии – два
опыта при двух как можно больше различающихся температурах (можно – по
краям заданного интервала). Значение среднего времени пребывания не влияет на
константы скорости и может быть задано на любом уровне. Чтобы обеспечить
достаточную точность расчета, нужно следить, чтобы концентрации, получаемые
в результате опытов, имели достаточно значащих цифр. Если вы видите, что зна-
чащих цифр мало (меньше трех), можете поменять время пребывания. Можно по-
рекомендовать брать маленькое время пребывания при большой температуре и
наоборот, в этом случае будет обеспечена близкая глубина превращения в двух
рассматриваемых опытах.
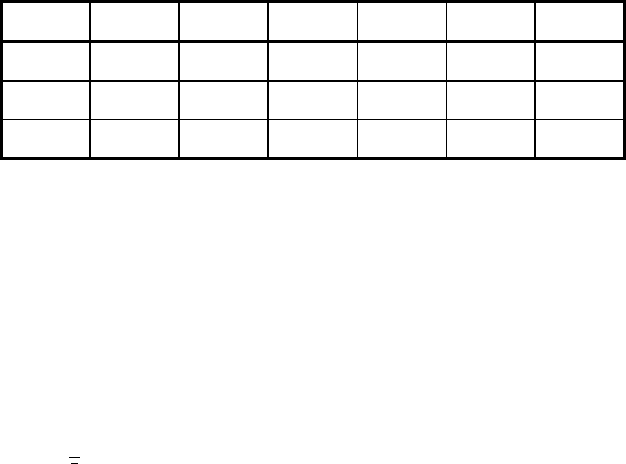
Результаты эксперимента сводятся в таблицу вида:
N
T t c
1
c
2
c
3
c
4
2.2. Обработка результатов эксперимента
Обработка результатов эксперимента начинается с решения системы урав-
нений математического описания реактора с целью определить значения констант
скоростей всех стадий реакции при двух температурах Таким образом, на первом
этапе расчета вы должны записать уравнения математического описания заданной
вам реакции для условий: поток – идеальное смешение, режим стационарный.
Математическое описание записывается в стандартной форме:
n
i
rcc
t
iii
..
1
0)(
1
0
=
=+−
(2.4)
где: i – номер вещества, t – среднее время пребывания, c
0i
, c
i
– концентрации
i-того вещества на входе и выходе из реактора, r
i
–скорость реакции по i-тому ве-
ществу.
Число уравнений равно числу веществ, участвующих в реакции (четырем).
Если теперь для каждого из опытов подставить в эти уравнения значения t и кон-
центраций – начальных, заданных в таблице исходных данных, и конечных, полу-
ченных в опыте, - то окажется, что уравнения содержат лишь три неизвестных:
константы скорости трех стадий. При их расчете можно исключить любое из че-
тырех уравнений. (Обратите внимание, что в исходных данных приведена на-
чальная концентрация только первого компонента; начальные концентрации дру-
гих веществ считаются равными 0).
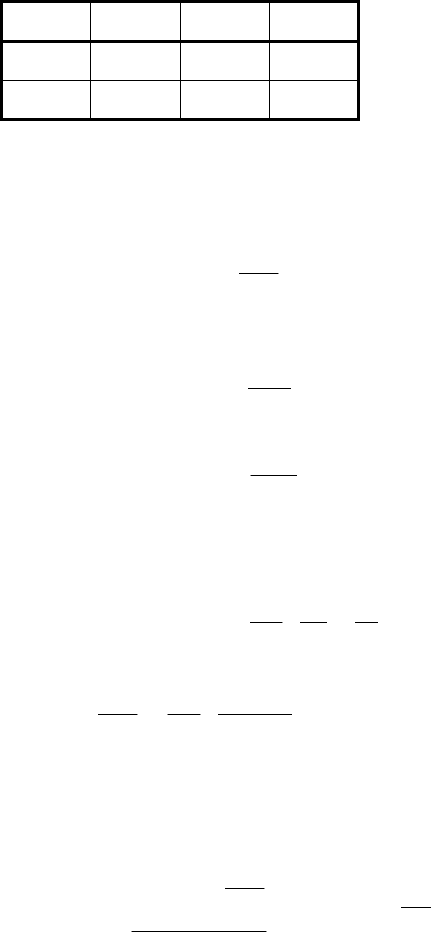
13
В результате этой стадии расчета вы получаете значения констант скорости
k
1
, k
2
и k
3
, которые целесообразно свести в таблицу:
T, K k
1
k
2
k
3
Затем вы переходите ко второму этапу расчета. Для расчета параметров
уравнения Аррениуса это уравнение приводится к линейному виду:
RT
E
kk
j
jj
−=
0
lnln (2.5)
Уравнение (2.5) записывается для двух температур:
1
0
lnln
1
RT
E
kk
j
j
T
j
−=
2
0
lnln
2
RT
E
kk
j
j
T
j
−=
Вычитая из первого уравнения второе получаем:
−
=
−=−
12
21
12
2
1
21
ln
11
lnln
TT
TT
R
E
k
k
TTR
E
kk
j
T
j
T
j
j
T
j
T
j
Окончательно:
12
21
1
2
ln
TT
k
k
TRT
E
T
j
T
j
j
−
= ,
11
0
RT
E
T
jj
a
ekk =
Нужно иметь в виду, что все промежуточные расчеты нужно делать с возможно
большей точностью, иначе ошибка расчета параметров может оказаться неприем-
лемой.
Рассчитав энергии активации и предэкспоненты для всех стадий реакции и
проверив правильность расчета, вы имеете весь набор исходной информации для
проведения следующих работ цикла.
2.3. Обсуждение результатов 2-й лабораторной работы.
Цель и задача работы, теоретическая часть и часть эксперимента описы
-
ваются как было указано ранее. Обратите внимание, что в экспериментальной

14
части следует привести все полученные в ходе работы данные и условия экспери-
ментов. Далее в отдельной таблице должны быть приведены два эксперимента,
выбранных для расчета (обоснование их выбора дается в обсуждении результа-
тов), а затем сами расчеты с обязательным сведением в таблицу полученных зна-
чений параметров уравнений Аррениуса, которые будут обсуждаться далее.
В обсуждении результатов 2-й лабораторной работы (расчет параметров
уравнения Аррениуса) можно выделить следующие опорные точки.
1. Выбор условий проведения опытов для получения максимального числа
значащих цифр во всех концентрациях. Большинство аналитических методов из-
мерения концентраций дают некую абсолютную погрешность при их измерении,
при этом относительная погрешность, очевидно, будет зависеть от величины из-
меряемого значения. Например, если метод позволяет измерить концентрацию с
точностью до 0.01 моль/л, то концентрация в 1 моль/л будет определена с по-
грешностью в 1%, в то время как 0.1 моль/л – уже в 10%. В представленной рабо-
те считается, что точность измерения составляет 10
–5
моль/л, соответственно, сле-
дует подбирать такие условия, чтобы измеренные концентрации превосходили
погрешность минимум на 3-4 порядка. Прежде чем приступать к расчетам, следу-
ет заранее составить систему уравнений, по которой будет осуществляться расчет
констант – может оказаться, что после отбрасывания лишнего уравнения какая-то
из концентраций окажется ненужной (разумно постараться выбрать удаляемое
уравнение именно таким образом) – в этом случае её величина не будет иметь
значения. Следует понимать, что в зависимости от системы реакций в заданных
интервалах времени и температур может в принципе не удаться получить все
концентрации >0.1 моль/л.
Кроме того, в работе рекомендуется выбирать как можно более различаю-
щиеся температуры. В эксперименте мы всегда с ограниченной точностью задаем
начальные условия и измеряем отклики системы – соответственно, погрешность
имеют как эти величины (в нашем случае температура и концентрации), так и ве-
личины, рассчитанные на их основе. Мы вычисляем параметры уравнения Арре-
ниуса из зависимости натурального логарифма константы от обратной температу-
ры, определяя фактически константы k и b в уравнении соответствующей прямой:
T
x
R
E
kkb
kxby
TR
E
kk
a
a
1
,,ln
1
)(lnln
0
0
=−==
+=
−+=
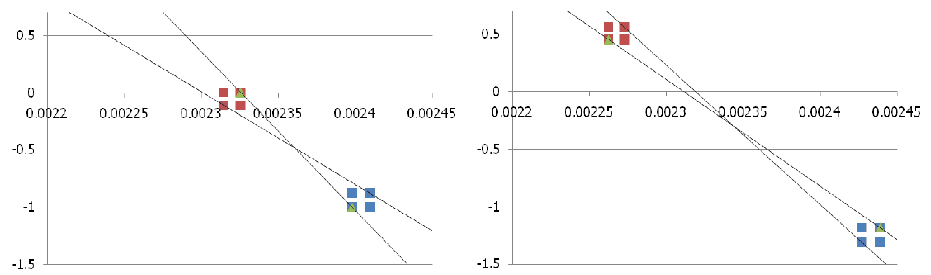
15
Т.е. x и y задаются с некоторой погрешностью, и две точки, которые мы ис-
пользуем для определения параметров прямой, на самом деле представляют собой
области, внутри которых заключены истинные значения. Приведенные графики
показывают «крайние» возможные положения прямых, проводимых через эти об-
ласти:
Рис. 2.1. Погрешность определения температуры – 2 градуса; (а) – темпера-
туры 415 и 430К, (б) – температуры 410 и 440К.
Как можно видеть из рисунка, прямые могут быть проведены под разным уг-
лом и, соответственно, отсекать разные отрезки на оси ординат, что соответствует
различным значениям b и k. Также легко заметить, что чем дальше отстоят точки,
тем меньше погрешность в определении этих параметров, чем и объясняется вы-
бор максимально различающихся температур для двух опытов.
Таким образом, первая часть обсуждения результатов представляет собой
обоснование выбора условий проведения экспериментов, её обобщением может
служить формулировка «Приведенным критериям в наибольшей степени отвеча-
ют эксперименты №… и … из таблицы 1, которые были использованы для даль-
нейших расчетов», либо, если опытов два, констатация того, что их достаточно.
2. Метод, используемый для расчетов. Программа моделирования решает
задачу, обратную стоящей перед вами: ей «известны» значения предэкспонент и
энергий активации, и она рассчитывает концентрации из той же системы уравне-
ний, что и вы, решая систему относительно концентраций. Решение осуществля-
ется методом Гаусса – при обсуждении результатов вы можете кратко изложить
суть метода (по желанию) и, по возможности, алгоритм его программирования
(также по желанию).
3. Оценка полученных результатов. Для этого полезно привлечь справоч-
ные данные по величинам предэкспонент и энергий активации реальных реакций
– это позволяет понять, лежат ли полученные значения в пределах, существую-
щих для соответствующих параметров. Также на основании параметров уравне-
ний Аррениуса можно сделать вывод о том, насколько быстро будет протекать та

16
или иная реакция в изучаемой системе, а также насколько сильно её скорость за-
висит от температуры. Это будет определять поведение системы при дальнейшем
изучении и поможет в трактовке получаемых результатов.
Вывод, как и ранее, должен представлять собой обобщение изложенного в
обсуждении результатов, но не являться повторением этого раздела.
Разумеется, предложенная схема анализа представляет собой всего лишь
один из возможных вариантов, и исследователь всегда имеет право предложить
свой.
Работа 3. Моделирование и исследование протекания сложной
реакции в аппаратах с различными гидродинамическими ре-
жимами
3.1. Объект исследования и эксперимент.
Реакция, заданная в работе 2, протекает в реакторе, который работает в ста-
ционарном изотермическом режиме. Известна схема реакции и кинетические ха-
рактеристики каждой стадии: порядок реакции (первый), энергия активации Е
а
и
предэкспоненциальный множитель уравнения Аррениуса k
0
. Целевой продукт –
вещество А
2
.
На процесс влияют два параметра: среднее время пребывания
t
и темпера-
тура Т. Для характеристики качества работы реактора можно использовать кон-
центрации продуктов на выходе из реактора, а также значения степени превраще-
ния, выхода и селективности. Интервал варьирования параметров задан в каждом
варианте расчета.
Необходимо исследовать работу реактора в заданных пределах изменения
времени пребывания и температуры, с тем, чтобы найти область наиболее эффек-
тивной его работы.
В качестве исходных данных используются:
1. Схема реакции. Реакция протекает в несколько стадий, каждая стадия, не-
зависимо от её стехиометрии, характеризуется первым порядком по исходному в
этой стадии веществу. Начальная концентрация 1-го вещества задается в условии
2-й лабораторной работы, начальные концентрации остальных компонентов рав-
ны 0.
2. Режим потока: идеальное смешение, идеальное вытеснение, каскад реак-
торов идеального смешения (ячеечная модель).

17
3. Значения энергий активации и предэкспоненциальных множителей урав-
нения Аррениуса для каждой стадии реакции, найденные в работе 2.
4. Границы области изменения параметров работы реактора: максимальные
и минимальные значения времени пребывания и температуры. При этом в первой
части (3.2) эта область задана в исходных данных, а в дальнейшем, после обсуж-
дения, может быть изменена.
Моделирование проводится последовательно для реактора идеального сме-
шения, затем для реактора идеального вытеснения, и, наконец, для каскада реак-
торов идеального смешения.
3.2. Реактор идеального смешения.
Исследование работы реактора начинают с режима идеального смешения.
Полученные результаты будут служить основой для сравнительной характеристи-
ки других режимов.
В нашем случае для изучения влияния времени пребывания и температуры
расчеты проводятся при пяти значениях каждого параметра. Это означает, что для
каждого значения одного параметра расчет проводится для пяти значений друго-
го. Имея начальную и конечную точки интервала для температуры, определяют
среднее между ними, что дает два интервала. Например, если исходный интервал
температур составляет 320-340К, получаем:
320 340 → 320 330 340
Проделав аналогичную операцию с этими двумя интервалами, получают
пять точек:
320 330 340 → 320 325 330 335 340
Таким же образом выбираются рабочие точки для второго параметра. В ре-
зультате получаем 25 рабочих точек, соответствующих т.н. плану полного фак-
торного эксперимента 5
2
.
Таким образом, мы имеем набор из 25 точек для расчета. Можно использо-
вать большее число точек – в этом случае отрезки делятся не на 4 части, а на 5, 6 и
т.д., а число точек составляет 36, 49… Большее число точек увеличивает трудоем-
кость расчета, однако позволяет получить более точные кривые и построить дос-
товерные контурные графики (см. далее).
Математическое описание в этой работе состоит из матрицы стехиометри-
ческих коэффициентов реакции, кинетических уравнений и уравнений матери-
ального баланса. Кинетические уравнения и уравнения материального баланса за-
писаны в расчетной программе и требуют только ввода значений параметров (па-

18
раметры уравнения Аррениуса, среднее время пребывания). Матрица стехиомет-
рических коэффициентов записывается в следующей форме:
=
nmmm
n
n
,2,1,
,22,21,2
,12,11,1
...
............
...
...
ααα
ααα
α
α
α
Α
где
ji,
α
- стехиометрические коэффициенты вещества j в стадии i, с учетом
знака (расходование или образование соответствующего вещества), n - число ве-
ществ, m - число стадий. Рассмотрим запись матрицы на конкретном примере.
Дана система реакций:
→
→
→
41
32
21
22
2
3
2
1
AA
AA
AA
k
k
k
В
первой
реакции
вещество
А
1
–
реагент
,
коэффициент
при
нем
1
и
оно
расходу
-
ется
–
следовательно
,
стехиометрический
коэффициент
составляет
–1.
Вещество
А
2
образуется
,
его
коэффициент
2
и
стехиометрический
коэффициент
+2.
Вещест
-
ва
А
3
и
А
4
не
участвуют
,
и
их
коэффициенты
– 0.
Аналогично
,
для
2-
й
реакции
ко
-
эффициенты
0, –1, 1, 0
и
т
.
д
.
Тогда
матрица
запишется
как
:
−
−
−
=
2002
0110
0021
Α
Задав матрицу стехиометрических коэффициентов, параметры ур-ния Ар-
рениуса для всех стадий, начальную концентрацию реагента А
1
и интервалы вре-
мени пребывания и температуры, необходимо осуществить расчет для выбранно-
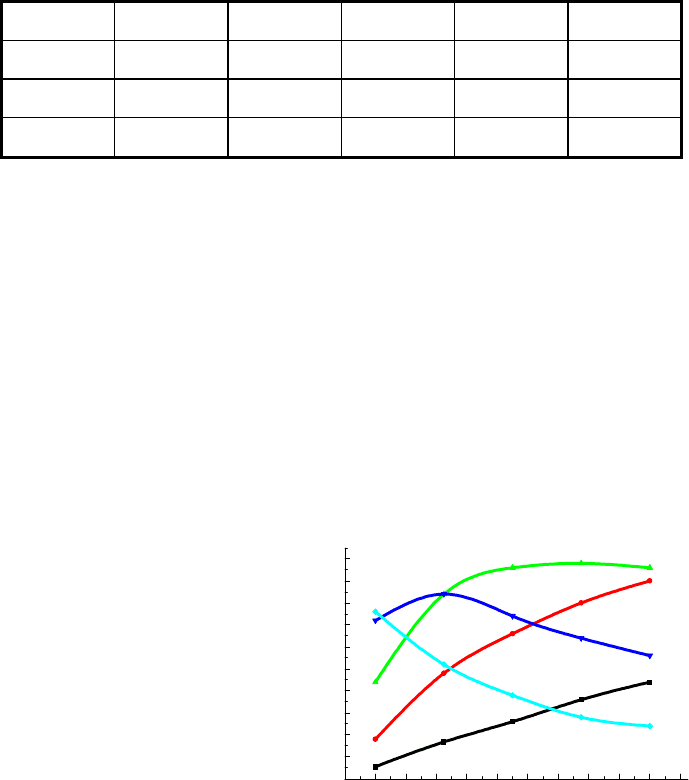
го числа точек. Результаты заносятся в две таблицы. Первая должна содержать
условия экспериментов и полученные на выходе концентрации всех компонентов,
конверсию (степень превращения)
P
, выход продукта
R
и селективность
S
.
N
t, с
T, К
Концентрации,
моль/л
P R S
c
1
c
2
c
3
c
4
1
... ... ... ... ... ... ... ... ... ...
25
19
Одновременно в небольшую таблицу записываются константы скорости (по
одному набору для каждой температуры, поскольку константы скорости реакций
не зависят ни от гидродинамического режима потока, ни от времени пребывания в
реакторе, что легко понять из их физического смысла). Рекомендуется в этой таб-
лице записывать конкретные значения Т.
T
1
T
2
T
3
T
4
T
5
k
1
k
2
k
3
Обработка результатов
Зависимости степени превращения, выхода и селективности (P,R,S) от вре-
мени и от температуры представляются на графиках. На каждом графике рисуется
зависимость одной характеристики от одного фактора (времени или температу-
ры), при нескольких постоянных значениях другого фактора. На графике получа-
ется несколько кривых (в рассматриваемой задаче – пять), например, как на рис.1,
где представлена зависимость выхода целевого продукта от времени пребывания
при пяти температурах.
0 2 4 6 8 10 12 14 16 18 20 22
0,00
0,05
0,10
0,15
0,20
0,25
0,30
0,35
0,40
0,45
0,50
T=433
T=408
T=383
T=358
T=333
t
R
Рис. 1. Зависимость выхода от времени при постоянной температуре.
Всего в работе получится шесть графиков: три для зависимости каждой ха-
рактеристики от времени и три – от температуры.
На графике гораздо нагляднее, чем в таблице, можно увидеть влияние на
рассматриваемые характеристики отдельно температуры и времени. Чтобы уви-
деть одновременное влияние этих двух параметров, можно было бы изобразить
трехмерный график, где по двум осям в горизонтальной плоскости отложены
температура и время, а по вертикальной оси – рассматриваемая характеристика.
Объемный трехмерный график построить сложно, поэтому его часто заменяют
построением контурного графика, который изображает поверхность в виде проек-
ции на горизонтальную плоскость изолиний этой поверхности. Тогда на одномер-
20
ном графике можно наглядно увидеть форму поверхности, как это используется
при рисовании географических карт (физических), где можно не только увидеть
характер рельефа, но и определить высоту каждой точки местности, пользуясь
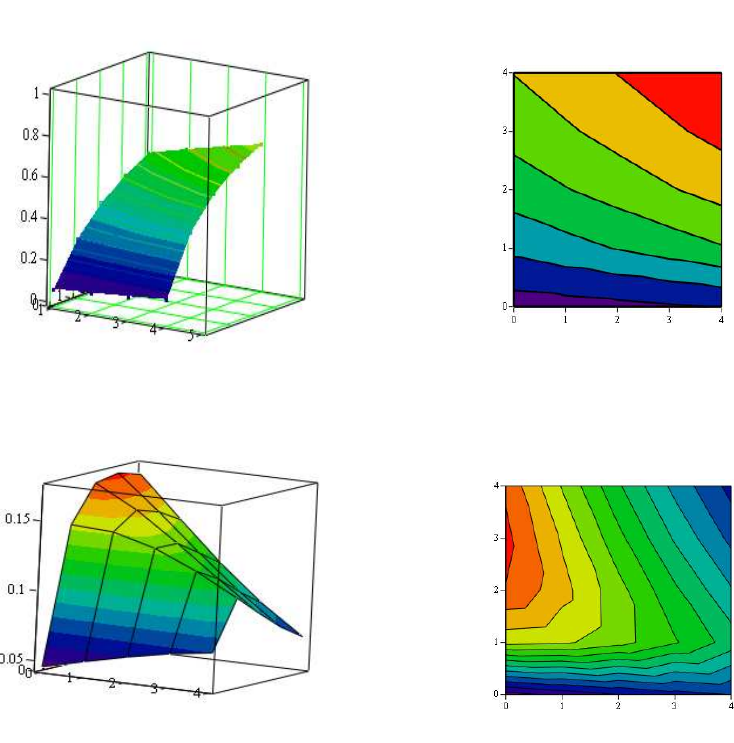
отметками на изолиниях (горизонталях). На рисунке 2 схематично представлены
некоторые поверхности и соответствующие им контурные графики:
→
χ
χ
→
η
Рис. 2. Трехмерные поверхности и соответствующие им контурные графики.
Техника построения контурных графиков состоит в следующем. Пусть име-
ется некоторая функция F от двух переменных x
1
и x
2
. Эта функция представлена
в виде двух однофакторных графиков (рис. 3 и 4). На рис. 3 в качестве примера
изображена та же зависимость, что и на рис. 1, рис. 4 соответствует зависимости
выхода от температуры при пяти значениях времени пребывания.
Выбираем несколько значений уровней функции F, для которых построим
линии уровней в координатах x
1
– x
2
. Линии уровней лучше выбирать таким обра-
зом, чтобы значения функции были «относительно круглыми» (т.е., например,
0.35, 0.5, 0.9 – нет смысла брать значения 0.358 и т.п.) – это облегчает анализ.
Кроме того, число пересечений линий с графиками должно быть как можно
больше – для этого нужно выбирать значения вблизи максимальных (но обяза-
η
η
