Засядко А.А., Петров А.В. Решебник. Теория вероятностей, математическая статистика и случайные процессы
Подождите немного. Документ загружается.

21
Свойство 2. Постоянный множитель можно выносить за знак математического ожи-
дания:
М(С·Х) = С·М (Х).
Свойство 3. Математическое ожидание произведения взаимно независимых случай-
ных величин равно произведению математических ожиданий сомножителей:
М(Х
1
·Х
2
·… ·Х
n
) = М(Х
1
) ·М (Х
2
) ·… ·М(Х
n
).
Свойство 4. Математическое ожидание суммы случайных величин равно сумме ма-
тематических ожиданий слагаемых:
М(Х
1
+Х
2
+… +Х
n
) = М(Х
1
) + М (Х
2
) + … + М(Х
n
).
Математическое ожидание биномиального распределения равно произведению числа
испытаний на вероятность появления события в одном испытании:
М(Х) = n·p.
Характеристиками рассеяния возможных значений случайной величины вокруг мате-
матического ожидания служат, в частности, дисперсия и среднее квадратическое отклонение.
Дисперсия случайной величины Х - это математическое ожидание квадрата отклоне-
ния случайной величины от ее математического ожидания:
D(X) = М[Х – М(Х)]².
Дисперсию удобно вычислять по формуле
D(X) = М(Х)² - [М(Х)]².
Дисперсия обладает следующими свойствами.
Свойство 1. Дисперсия постоянной равна нулю:
D(C) =0
Свойство 2. Постоянный множитель можно выносить за знак дисперсии, предвари-
тельно возведя его в квадрат:
D(C·Х) = С²·D(Х).
Свойство 3. Дисперсия суммы независимых случайных величин равна сумме диспер-
сий слагаемых:
D(Х
1
+Х
2
+… +Х
n
) = D(Х
1
) + D(Х
2
) + … + D(Х
n
).
Дисперсия биномиального распределения равна произведению числа испытаний на
вероятности появления и непоявления события в одном испытании:
D(Х) =n·p·q.
Средним квадратическим отклонением случайной величины называют квадратный
корень из дисперсии:
σ(Х) = .D(X)
РЕШЕНИЕ ЗАДАЧ
1. Найти математическое ожидание дискретной случайной величины Х, заданной за-
коном распределения:
а) Х -4 6 10 б) Х 0,21
0,54
0,61
Р 0,2 0,3 0,5 P 0,1 0,5 0,4
Решение.
Математическое ожидание равно сумме произведений всех возможных значений Х на
их вероятности:
а) М(Х) = -4 ⋅0,2 + 6⋅0,3 + 10⋅0,5 = 6.
б) М(Х) = 0,21⋅0,1 + 0,54⋅0,5 + 0,61⋅0,4 =0,535.
Ответ: а) 6; б) 0,535.
2. Доказать, что если случайные величины Х
1
, Х
2
, … Х
n
независимы, положительны и
одинаково распределены, то
М [Х
1
/ Х
1
+Х
2
+… Х
n
] = 1/n.
22
Решение.
Введем в рассмотрение случайные величины
Y
1
= Х
1
/ (Х
1
+ Х
2
+…+ Х
n
), Y
2
= Х
2
/ (Х
1
+ Х
2
+…+ Х
n
), …, Y
n
= Х
n
/ (Х
1
+ Х
2
+…+ Х
n
) (*)
Заметим, что знаменатели этих дробей не могут быть равными нулю, поскольку вели-
чины Х
i
(i=1,2,…n) положительны.
По условию, величины Х
i
одинаково распределены, поэтому и величины Y
i
также
одинаково распределены и, следовательно, имеют одинаковые числовые характеристики, в
частности, одинаковые математические ожидания:
М(Y
1
) = М(Y
2
) = … = М(Y
n
) (**)
Легко видеть, что Y
1
+ Y
2
+… + Y
n
=1, следовательно,
М(Y
1
+Y
2
+ … Y
n
) =М(1) =1.
Математическое ожидание суммы равно сумме математических ожиданий слагаемых,
поэтому
М(Y
1
) + М(Y
2
)+ … +М(Y
n
) = 1.
В силу (**) имеем n·М(Y
1
) =1. Отсюда М(Y
1
)=1/n.
Учитывая (*), окончательно получим:
М[Х
1
/ (Х
1
+ Х
2
+…+ Х
n
)] = 1/n.
Доказано.
3. Найти дисперсию и среднеквадратическое отклонение дискретной случайной вели-
чины Х, заданной законом распределения:
а) Х 4,3 5,1 10,6
б) X 131 140 160 180
Р 0,2 0,3 0,5 P 0,005
0,10
0,25
0,60
Решение.
Дисперсию удобно вычислять по формуле
D(X) = М(Х)² - [М(Х)]².
Найдем математическое ожидание:
а) М(Х) = 4,3⋅0,2+5,1·0,3 +10,6⋅0,5 = 7,69
б) М(Х) = 131·0,05 + 140·0,1 + 160⋅0,25 + 180⋅0,6= 168,55
Напишем закон распределения для Х²:
а) Х
2
18,49
26,01
112,36
б) X
2
17161
19600
25600
32400
Р 0,2 0,3 0,5 P 0,005 0,10 0,25 0,60
Найдем математическое ожидание для Х²:
а) М(Х²) = 3,698 + 7,803 + 56,18 =67,681
б) М(Х²) = 19440 + 6400 + 1960 + 858, 05 = 28658, 05.
Искомая дисперсия:
а) D(X) = 67,681 –(7,69)² = 8,5449
σ(Х) = √ D(X) =2,92
б) D(X) = 28658,05 –28409,1025 = 248,94
σ(Х) = 15,77.
Ответ: а) D(X) = 8,5449, σ(Х) =2,92; б) σ(Х) =15,77, D(X) =248,94.
4. Найти дисперсию дискретной случайной величины Х, распределенной по закону
Пуассона:
X
0 1 …
K
P e
–λ
·λ·e
-λ
/1!
λ²· e
-λ
/2!
…
λ
-
k·e
-λ
/k!
Решение.
Воспользуемся формулой D(X) =М(Х²) – [М(Х)]².
Так как М(Х) =λ, то
23
D(X) = М(Х²) – λ² (*)
Напишем распределение случайной величины Х², учитывая, что вероятность того, что
Х² примет значение k², равна вероятности того, что Х примет значение k (это следует из того,
что возможные значения Х неотрицательны):
X
2
0
2
1
2
…
K
2
P e
–λ
·λ·e
-λ
/1!
λ²· e
-λ
/2!
…
λ
-
k·e
-λ
/k!
Найдем математическое ожидание Х²:
М(Х²) = .
!
k
ek
k2
λ
−
∑
⋅λ⋅
Учитывая, что при k=0 первый член суммы равен нулю, получим
М(Х²) =
∑
λ−
⋅λ⋅
!
k
ek
k2
=
∑
−⋅
⋅λ⋅
λ−
)!1k(k
ek
k2
=
∑
−
⋅λ⋅
⋅λ
λ−−
)!1k(
ek
1k
=
=
∑
−
⋅λ⋅+−
⋅λ
λ−−
)!1k(
e]1)1k[(
1k
= .
)!1k(
e)1k(
1k
∑
−
⋅λ⋅−
⋅λ
λ−−
Положив k-1=m, имеем
М(Х²) =λ·
⋅λ
+
⋅λ⋅
∑∑
λ−λ−
!m
e
!m
em
mm
.
Принимая во внимание, что
∑
λ=
⋅λ⋅
λ−
,
!
m
em
m
∑
=⋅=
∑
λ
=
⋅λ
λλ−⋅λ−
λ−
.1ee
!
m
e
!
m
e
mm
имеем
М(Х²) =λ·(λ+1) = λ² +λ (**)
Подставим (**) в (*):
D(X) = (λ² + λ) –λ² = λ.
Итак, дисперсия распределения Пуассона равна параметру λ.
4.4. Теоретические моменты.
Краткие теоретические сведения.
Начальным маментом порядка k случайной величины Х называют математическое
ожидание величины Х
k
:
ν
k
= М(Х
k
).
В частности, начальный момент первого порядка равен математическому ожиданию:
ν
1
= М(Х).
Центральный момент порядка k случайной величины Х называют математическое
ожидание величины [X –M(X)]
k
:
μ
k
= М [Х - М(Х)]
k
.
В частности, центральный момент первого порядка равен нулю:
μ
1
= М [Х - М(Х)] = 0;
центральный момент второго порядка равен дисперсии:
μ
2
= М [Х - М(Х)]
2
= D(X).
Центральные моменты целесообразно вычислять, используя формулы, выражающие
центральные моменты через начальные:
μ
2
= ν
2
-ν
1
²,
μ
3
= ν
3
- 3·ν
1
·ν
2
+ 2·ν
3
1
,

24
μ
4
= ν
4
–4·ν
1
·ν
3
+ 6ν²
1
·ν2
–3·ν
4
1
.
РЕШЕНИЕ ЗАДАЧ
1. Дискретная случайная величина Х задана законом распределения:
X
1 3
P 0,4
0,6
Найти начальные моменты первого, второго и третьего порядков.
Решение.
Найдем начальный момент первого порядка:
ν
1
= М(Х) = 1⋅0,4 +3⋅0,6 =2,2.
Напишем закон распределения величины Х²:
X
2
1 9
P 0,4
0,6
Найдем начальный момент второго порядка:
ν
2
= М(Х²) =1⋅0,4 + 9⋅0,6 =5,8.
Напишем закон распределения величины Х
3
:
X
3
1 27
P 0,4
0,6
Найдем начальный момент третьего порядка:
ν
3
= М(Х
3
) =1⋅0,4 + 27⋅0,6 =16,6.
Ответ: ν
1
=2,2; ν
2
=5,8; ν
3
=16,6.
2. Дискретная случайная величина Х задана законом распределения:
X
3 5
P 0,2
0,8
Найти начальные моменты первого, второго, третьего и четвертого порядков.
Указание. Найти предварительно начальные моменты и выразить через них централь-
ные моменты.
Решение.
μ
1
=0. Найдем начальные моменты:
ν
1
= М(Х) = 3·0,2 + 5⋅0,8 = 4,6
ν
2
= М(Х²) = 9⋅0,2 +25⋅0,8 =21,8
ν
3
= М(Х
3
) =27⋅0,2 + 125⋅0,8 = 105,4
ν
4
= М(Х
4
) = 81⋅0,2 + 625⋅0,8 =516,2.
Найдем центральные моменты:
μ
2
= ν
2
-ν
1
² = 21,8 –21,16 =0,64
μ
3
= ν
3
- 3ν
1
ν
2
+ 2ν
3
1
= 105,4 –300,84 +194,67 = -0,768
μ
4
= ν
4
–4ν
1
ν
3
+ 6ν²
1
ν
2
–3ν
4
1
= 516,2 – 1939,36 +2767,72 – 1343,23 = 1,323.
Ответ: 0; 0,64; -0,77; 1,33.
Контрольные вопросы.
1. Какая величина называется центральным моментом?
2. Какая величина называется дисперсией?
3. Какая величина называется математическим ожиданием?
4. В чем состоит свойство стационарности?
5. Что называется потоком событий? Простейшим потоком событий?
6. Какими свойствами обладает дисперсия?
25
5. ЗАКОН БОЛЬШИХ ЧИСЕЛ
5.1. Неравенство Чебышева.
Цель: уяснить основные определения, применение неравенства и теоремы Чебышева
в теории вероятностей.
Краткие теоретические сведения.
Неравенство Чебышева. Вероятность того, что отклонение случайной величины Х от
ее математического ожидания по абсолютной величине меньше положительного числа ε, не
меньше чем
2
)X(D
1
ε
− :
2
)X(D
1))X(MX(P
ε
−≥ε<− .
РЕШЕНИЕ ЗАДАЧ
1. Используя неравенство Чебышева, оценить вероятность того, что случайная вели-
чина Х отклонится от своего математического ожидания менее чем на три среднеквадратиче-
ских отклонения.
Решение.
( )
.
3
22
)X(D)X(
.
9
8
9
1
1
)3(
1)3()X(MXP
2
2
2
==
=−=
⋅
−≥⋅<−
σ
σ
σ
σ
2. Доказать неравенство Чебышева в форме
.
)X(D
))X(MX(P
2
ε
≤ε≥−
Решение.
.
)X(D
))X(MX(P
2
ε
≤ε≥−
2
)X(D
1))X(MX(P
ε
−≥ε<−
),)X(MX(P1
)X(D
2
ε<−−≥
ε
).)X(MX(P
)X(D
),)X(MX(P))X(MX(P1
2
ε≥−≥
ε
ε≥−=ε<−−
Доказано.
3. В осветительную сеть параллельно включено 20 ламп. Вероятность того, что за
время Т лампа будет включена, равна 0,8. Пользуясь неравенством Чебышева, оценить веро-
ятность того, что абсолютная величина разности между числом включенных ламп и средним
числом (математическим ожиданием) включенных ламп за время Т окажется: а) меньше
трех; б) не меньше трех.
Решение.
Обозначим через Х дискретную случайную величину - число включенных ламп -как

26
Т. Тогда
М(Х) =n·p = 20·0,8 =16
D(X) = n·p·q = 20·0,8·0,2 = 3,2.
Воспользуемся неравенством Чебышева:
Р(|X - M(X)| < ε) ≥ 1-D(X) /ε².
Р (|X-16| <3)≥ 1-3,2/9 ≥ 0,64.
События |X-16|<3 и |X-16|≥3 противоположны, следовательно сумма их вероятностей
равна единице:
Р(|X-16| ≥ 3) ≤ 1 –0,64 ≤ 0,36.
Ответ: а) ≥ 0,64; б) ≤ 0,36.
5.2. Теорема Чебышева.
Краткие теоретические сведения.
Теорема Чебышева. Если последовательность попарно независимых случайных вели-
чин Х
1
, Х
2
… Х
n
,… имеет конечные математические ожидания и дисперсии этих величин
равномерно ограничены (не превышают постоянного числа С), то среднее арифметическое
случайных величин сходится по вероятности к среднему арифметическому их математиче-
ских ожиданий, т.е. если ε - любое положительное число, то
.1)X(M
n
1
X
n
1
P
i
i
i
i
n
lim
=
<⋅−⋅
∑∑
∞→
ε
В частности, среднее арифметическое последовательности попарно независимых ве-
личин, дисперсии которых равномерно ограничены и которые имеют одно и то же математи-
ческое ожидание а, сходится по вероятности к математическому ожиданию а, т.е. если ε -
любое положительное число, то
.1aX
n
1
P
i
i
n
lim
=
<−⋅
∑
∞→
ε

27
6. ФУНКЦИИ И ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ
ВЕРОЯТНОСТЕЙ СЛУЧАЙНЫХ ВЕЛИЧИН.
6.1. Функция распределения вероятностей случайной величины.
Цель: уяснить основные определения, применение неравенства и теоремы Чебышева
в теории вероятностей.
Краткие теоретические сведения.
Функцией распределения называют функцию F(x), определяющую для каждого значе-
ния х вероятность того, что случайная величина Х примет значение, меньшее х, т.е. F(x) = P
(X<x).
Часто вместо термина «функция распределения» используют термин «интегральная
функция распределения».
Функция распределения обладает следующими свойствами:
Свойство 1. Значения функции распределения принадлежат отрезку [0;1]:
0≤ F(x) ≤ 1
Cвойство 2. Функция распределения есть неубывающая функция:
F(x
2
) ≥ F(x
1
), если x
2
> x
1
.
Следствие 1. Вероятность того, что случайная величина Х примет значение, заклю-
ченное в интервале (a,b), равна приращению функции распределения на этом интервале:
Р(a<X<b) = F(b) – F(a).
Следствие 2. Вероятность того, что непрерывная случайная величина Х примет одно
определенное значение, например x
1
, равна нулю:
Р(Х= x
1
) = 0
Свойство 3. Если все возможные значения случайной величины Х принадлежат ин-
тервалу (a,b), то
F(x) =0 при x ≤ a; F(x) = 1 при x ≥ b.
Следствие. Справедливы следующие предельные соотношения:
lim F(x) = 0 при х → - ∞, lim F(x) = 1 при х→ ∞.
Свойство 4. Функция распределения непрерывна слева:
lim F(x) = F(x
0
) при х ↑ x
0
.
РЕШЕНИЕ ЗАДАЧ
1. Случайная величина Х задана функцией распределения
>
≤<+⋅
≤
=
.
3
1
xпри ,1
,
3
1
x1- при ,
4
3
x
4
3
,1- xпри ,0
)X(F
Найти вероятность того, что в результате испытания величина Х примет значение, за-
ключенное в интервале (0, 1/3).
Решение.
Вероятность того, что Х примет значение, заключенное в интервале (a;b), равна при-
ращению функции распределения на этом интервале: Р(a<X<b) = F(b) - F(a). Положив a= 0,
b=1/3, получим
Р(0<X<1/3) = F(1/3) – F(0) = [(3/4)⋅x + 3/4]
х =1/3
–[ (3/4)⋅x + 3/4]
х =0
=1/4.
Ответ:
.
4
1
28
2. Случайная величина Х задана на всей оси Ох функцией распределения F(x)=1/2+
+(arctgx)/π. Найти вероятность того, что в результате испытания величина Х примет значе-
ние, заключенное в интервале (0,1).
Решение.
Вероятность того, что Х примет значение, заключенное в интервале (a;b), равна при-
ращению функции распределения на этом интервале: Р(a<X<b) = F(b) - F(a). Следовательно,
Р(0<X<1) = F(1) – F(0) = [1/2+ (arctg 1)/π] – [1/2+ (arctg 0)/π ] =
.
4
1
Ответ:
.
4
1
3. Функция распределения непрерывной случайной величины Х (времени безотказной
работы некоторого устройства) равна F(x) = 1 – e
-x /T
(x ≥ 0). Найти вероятность безотказной
работы устройства за время х ≥ Т.
Решение.
Р(х ≥Т) = 1 – Р(х<T) = 1 – P (0< x <T) = e
-x /T
.
Ответ: e
-x /T
.
4. Дискретная случайная величина задана законом распределения
X
3 4 7 10
P 0,2
0,1
0,4
0,3
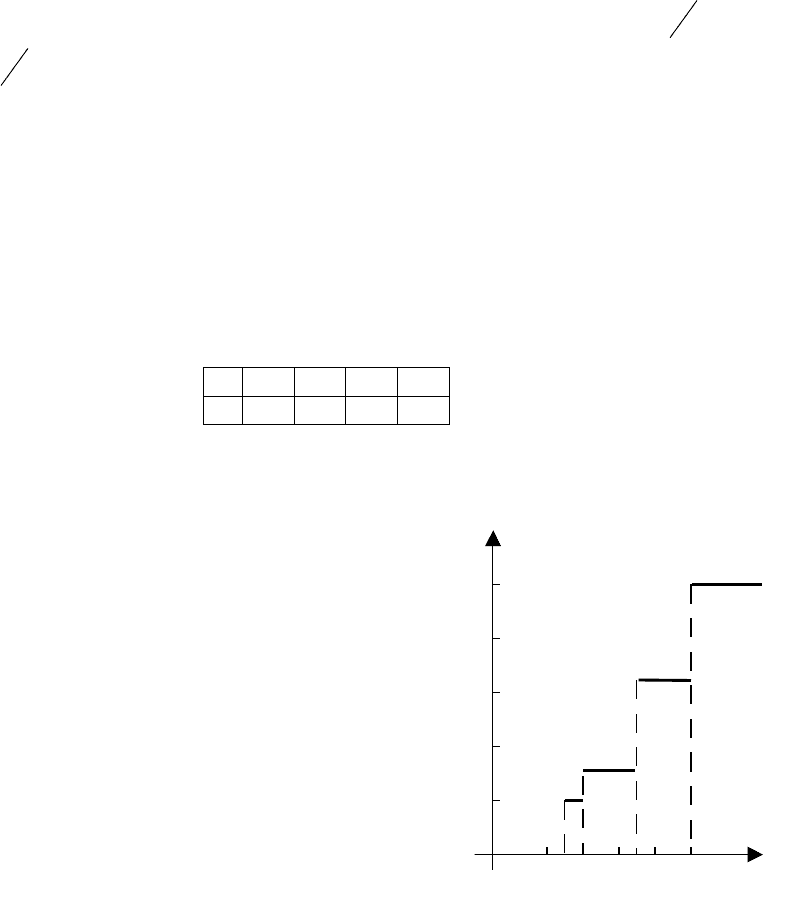
Найти функцию распределения и построить ее график.
Решение.
1. Если х ≤ 3, то F(x)= 0, т.к. величина х не
принимает значений меньше 3.
2. Если 3 < x ≤ 4, то F(x) =0,2, т.е. х может
принимать значение 3 с вероятностью 0,2.
3. Если 4< x ≤ 7, то F(x) =0,3. Действительно, х
может принимать значение 3 с вероятно-
стью 0,2 и значение 4 с вероятностью 0,1;
следовательно, одно из этих значений,
безразлично какое, Х может принимать (по
теореме сложения вероятностей несовмест-
ных событий) с вероятностью 0,1 + 0,2 =0,3
4. Если 7< x ≤ 10, то F(x) =0,7 (0,2+0,1+0,4).
5. Если х > 10, то F(x) = 1.
Итак, искомая функция распределения имеет
вид
>
≤<
≤<
≤<
≤
=
.01 xпри ,1
,01x7 при ,7,0
7,x4 при ,3,0
4,x3 при ,2,0
,3 xпри ,0
)X(F
Рис. 7.1. Функция распределения.
Задача 4.
F(X)
1
0,8
0,6
0,4
0,2
0 2 4 6 8 10 x

29
6.2. Плотность распределения вероятностей непрерывной случайной величины.
Краткие теоретические сведения.
Плотностью распределения вероятностей непрерывной случайной величины называ-
ют первую производную от функции распределения f(x) = F’(x).
Часто вместо термина «плотность распределения» используют термины «плотность
вероятностей» и «дифференциальная функция».
Вероятность того, что непрерывная случайная величина Х примет значение, принад-
лежащее интервалу (а, b) определяется равенством
.dx)x(f)bXa(P
b
a
∫
⋅=<<
Зная плотность распределения, можно найти функцию распределения
.dz)z(f)X(F
x
∫
∞
−
⋅=
Плотность распределения обладает следующими свойствами:
Свойство 1. Плотность распределения неотрицательна, т.е. f(x) ≥ 0.
Свойство 2. Несобственный интеграл от плотности распределения в пределах от -∞
до ∞ равен единице.
В частности, если все возможные значения случайной величины принадлежат интер-
валу (a,b), то
.1dx)x(f
b
a
=⋅
∫
РЕШЕНИЕ ЗАДАЧ
1. Дана функция распределения непрерывной случайной величины Х
π
>
π
≤<
≤
=
.
2
xпри ,1
,
2
x0 при ),xsin(
,0 xпри ,0
)X(F
Найти плотность распределения f(x).
Решение.
Плотность распределения равна первой производной от функции распределения:
π
>
π
≤<
≤
=
.
2
xпри ,0
,
2
x0 при ),xcos(
,0 xпри ,0
)X(f
Заметим, что при х=0 производная F’(x) не существует.

30
2. Задана плотность распределения непрерывной случайной величины Х:
π
>
π
≤<
≤
=
.
2
xпри ,0
,
2
x0 при ),xcos(
,0 xпри ,0
)X(f
Найти функцию распределения F(x).
Решение.
Используем формулу
.dz)z(f)X(F
x
∫
∞
−
⋅=
Если х ≤0, то f(x) =0, следовательно,
.dz0)X(F
0
∫
∞
−
⋅=
Если 0< x ≤ π /2, то
).xsin(dz)xcos(dz0)X(F
x
0
0
=⋅+⋅=
∫∫
∞−
Если x > π /2, то
.1dz0dz)xcos(dz0)X(F
x
2
2
0
0
=⋅+⋅+⋅=
∫∫∫
π
π
∞−
Итак, искомая функция распределения:
π
>
π
≤<
≤
=
.
2
xпри ,1
,
2
x0 при ),xsin(
,0 xпри ,0
)X(F
6.3. Числовые характеристики непрерывных случайных величин.
Краткие теоретические сведения.
Математическое ожидание непрерывной случайной величины Х, возможные значения
которой принадлежат всей оси Ох, определяется равенством
,dx)x(fx)X(M
∫
+∞
∞
−
⋅⋅=
