Засядко А.А., Петров А.В. Решебник. Теория вероятностей, математическая статистика и случайные процессы
Подождите немного. Документ загружается.


31
где f(x) –плотность распределения случайной величины Х. Предполагается, что интеграл
сходится абсолютно.
В частности, если все возможные значения принадлежат интервалу (а, b)
,dx)x(fx)X(M
b
a
∫
⋅⋅=
Все свойства математического ожидания, указанные выше для дискретных случайных
величин (см. п.4.1), сохраняются и для непрерывных величин.
Если Y = φ(X) - функция случайного аргумента Х, возможные значения которого при-
надлежат всей оси Ох, то
[ ]
.dx)x(f)x()X(M
∫
+∞
∞
−
⋅⋅ϕ=ϕ
В частности, если возможные значения Х принадлежат интервалу (а,b), то
[ ]
.dx)x(f)x()X(M
b
a
∫
⋅⋅ϕ=ϕ
Если математическое ожидание М(Х) существует и кривая распределения симмет-
рична относительно прямой х = С, то М(Х) = С.
Модой М
0
(Х) непрерывной случайной величины Х называют то ее возможное значе-
ние, которому соответствует локальный максимум плотности распределения. В частности,
если распределение имеет два одинаковых максимума, то его называют бимодальным.
Медианой М
е
(Х) непрерывной случайной величины Х называют то ее возможное зна-
чение, которое определяется равенством
Р[ X< М
е
(Х) ] = P[ X > М
е
(Х) ].
Геометрически медиану можно истолковать как точку, в которой ордината f(x) делит
пополам площадь, ограниченную кривой распределения.
Дисперсия непрерывной случайной величины Х, возможные значения которой принад-
лежат всей оси Ох, определяется равенством
[ ]
∫
+∞
∞
−
⋅⋅−= dx)x(f)X(MX)X(D
2
или равносильным равенством
).X(Mdx)x(fX)X(D
22
−
⋅⋅=
∫
∞+
∞−
В частности, если все возможные значения Х принадлежат интервалу (а, b), то
[ ]
∫
⋅⋅−=
b
a
2
dx)x(f)X(MX)X(D или ).X(Mdx)x(fX)X(D
2
b
a
2
−
⋅⋅=
∫
Все свойства дисперсии, указанные выше для дискретных случайных величин (см.
тема 4, §3), сохраняются и для непрерывных величин.
Среднее квадратическое отклонение непрерывной случайной величины определяется
так же, как и для дискретной величины:
.)X(D)X( =σ
Если Y = φ (X) - функция случайного аргумента Х, причем возможные значения Х
принадлежат всей оси Ох, то

32
[] [][ ]
∫
+∞
∞
−
⋅⋅ϕ−ϕ=ϕ dx)x(f)X(M)X()X(D
2
или
[ ] [ ]
.)X(Mdx)x(f)X()X(D
22
ϕ−
⋅⋅ϕ=ϕ
∫
∞+
∞−
В частности, если все возможные значения Х принадлежат интервалу (а, b), то
[ ] [ ][ ]
∫
⋅⋅ϕ−ϕ=ϕ
b
a
2
dx)x(f)X(M)X()X(D
или
[ ] [ ]
.)X(Mdx)x(f)X()X(D
2
b
a
2
ϕ−
⋅⋅ϕ=ϕ
∫
Начальный теоретический момент порядка k непрерывной случайной величины Х оп-
ределяется равенством
.dx)x(fx
k
k
∫
+∞
∞
−
⋅⋅=ν
Центральный теоретический момент порядка k непрерывной случайной величины Х
определяется равенством
[ ]
∫
+∞
∞
−
⋅⋅−=µ dx)x(f)X(MX
k
k
В частности, если все возможные значения Х принадлежат интервалу (а, b), то
∫
⋅⋅=ν
b
a
k
k
dx)x(fx и
[ ]
.dx)x(f)X(MX
b
a
k
k
∫
⋅⋅−=µ
Очевидно, что если k =1, то ν
1
= М(Х), μ
1
=0; если k=2, то μ
2
=D(X).
Центральные моменты выражаются через начальные моменты по формулам:
μ
2
= ν
2
-ν
1
²,
μ
3
= ν
3
- 3ν
1
⋅ν2
+ 2ν
3
1
,
μ
4
= ν
4
–4ν
1
⋅ν
3
+ 6ν²
1
⋅ν
2
–3ν
4
1
.
РЕШЕНИЕ ЗАДАЧ.
1. Случайная величина Х задана плотностью распределения f(x) =2x в интервале (0,1);
вне этого интервала f(x) = 0. Найти математическое ожидание величины Х.
Решение.
Используем формулу
,dx)x(fx)X(M
b
a
∫
⋅⋅=
подставив а =0, b = 1, f(x) =2x, получим
.
3
2
dxx2)X(M
b
a
2
=⋅⋅=
∫
Ответ: 2/3.
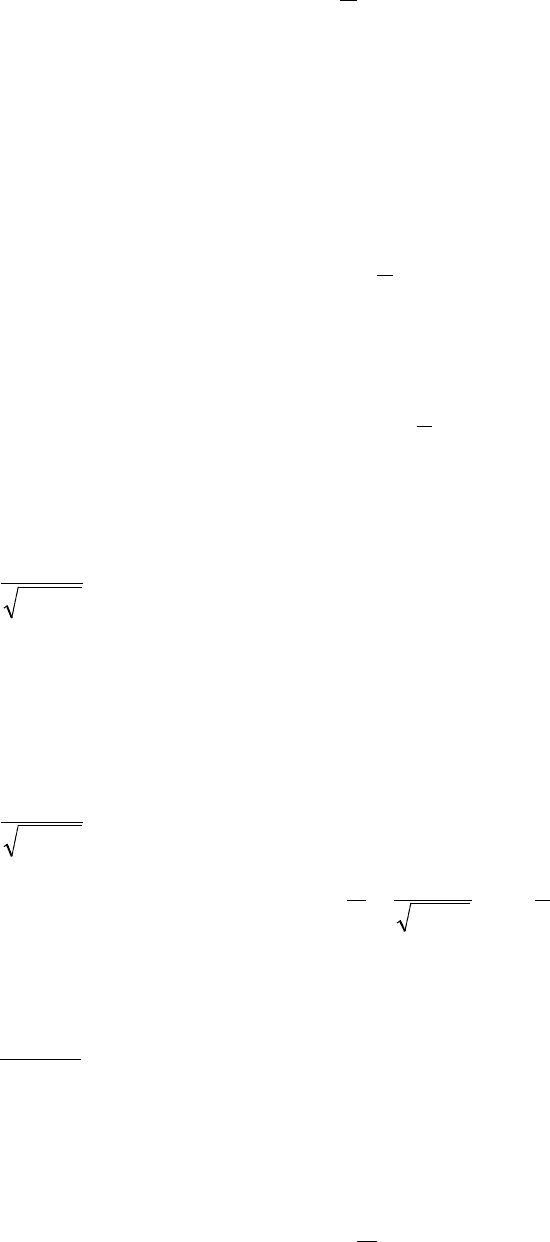
33
2. Найти математическое ожидание случайной величины Х, заданной функцией рас-
пределения
>
≤<
≤
=
.4 xпри ,1
,4x0 при ,
4
x
,0 xпри ,0
)X(F
Решение.
Найдем плотность распределения величины Х:
>
≤<
≤
==
.4 xпри ,0
,4x0 при ,
4
1
,0 xпри ,0
)X('F)x(f
Искомое математическое ожидание:
.2dx
4
1
x)X(M
4
0
=⋅⋅=
∫
Ответ: 2.
3. Случайная величина Х в интервале (-3,3) задана плотностью распределения
2
x9
1
)x(f
−
= ; вне этого интервала f(x) = 0. Найти дисперсию Х.
Решение.
Найдем дисперсию по формуле
[ ]
∫
⋅⋅−=
b
a
2
dx)x(f)X(MX)X(D .
Подставляя М(Х) =0 (кривая симметрична относительно прямой х=0), а = -3, b =3,
2
x9
1
)x(f
−
= , получим
∫
−
=⋅
−
⋅=
3
3
2
2
.
2
9
dх
x9
x1
)X(D
π
Ответ: 4,5.
4. Случайная величина Х в интервале (-3,3) задана плотностью распределения
!
n
ex
)x(f
xn −
⋅
= при х ≥ 0; f(x)= 0 при х < 0. Найти: а) математическое ожидание; б) диспер-
сию Х.
Решение.
а) Найдем математическое ожидание:
.dxex
!n
1
)X(M
0
x1n
∫
+∞
−+
⋅⋅⋅=

34
Воспользуемся так называемой гамма-функцией, которая определяется равенством:
.dxex)n(
0
x1n
∫
+∞
−−
⋅⋅=Γ (*)
Как видим, аргумент (целое число n), стоящий под знаком гамма-функции, на едини-
цу больше показателя степени буквы х, стоящей под знаком интеграла. Следовательно,
.dxex)2n(
0
x1n
∫
+∞
−+
⋅⋅=+Γ (*)
Подставив (**) в (*), получим
.
!
n
)2n(
)X(M
+
Γ
= (***)
Воспользуемся следующими свойствами гамма-функции:
Г(n) = (n-1)!
Как видим, гамма-функция от целого аргумента равна факториалу от аргумента,
уменьшенного на единицу. Следовательно,
Г(n+2) = (n-1)! (****)
Подставив (****) в (***), получим
.1n
!
n
)1n(!n
!
n
)!1n(
)X(M +=
+
⋅
=
+
=
б) Найдем дисперсию. Учитывая, что
М(Х) = n+1 и ,dxex)3n(
0
x2n
∫
+∞
−+
⋅⋅=+Γ
получим
.1n)!1n(
n!
2)!(n
)1n(
!n
)3n(
)1n(dxex
!n
1
)X(Mdx)x(fx)X(D
22
0
x2n2
0
2
+=+−
+
=
=+−
+Γ
=+−
⋅⋅⋅=−
⋅⋅=
∫∫
∞+
−+
∞+
Итак, D(X) = n+1.
Ответ: М(Х) =n+1, D(X) =n+1.
5. Случайная величина Х задана плотностью распределения f(x) =0,5x в интервале
(0,2); вне этого интервала f(x)=0. Найти начальные и центральные моменты первого, второго,
третьего и четвертого порядков.
Решение.
По формуле
∫
⋅⋅=ν
2
0
k
k
dx)x(fx .
Найдем начальные моменты:

35
3
4
dxx5,0x
2
0
1
=⋅⋅⋅=ν
∫
,
∫
=⋅⋅⋅=ν
2
0
2
2
2dxx5,0x ,
∫
=⋅⋅⋅=ν
2
0
3
3
2,3dxx5,0x ,
∫
=⋅⋅⋅=ν
2
0
4
4
3
16
dxx5,0x .
Найдем центральные моменты. Центральный момент первого порядка любой случай-
ной величины равен нулю.
Воспользуемся формулами, выражающими центральные моменты через начальные:
μ
2
= ν
2
-ν
1
²,
μ
3
= ν
3
- 3ν
1
⋅ν
2
+ 2ν
3
1
,
μ
4
= ν
4
–4ν
1
⋅ν
3
+ 6ν²
1
⋅ν
2
–3ν
4
1
.
Подставив в эти формулы ранее найденные начальные моменты, получим:
μ
2
= 2/9; μ
3
= -8/135; μ
4
= 16/135.
Ответ: ν
1
=4/3; ν
2
=2; ν
3
= 3,2; ν
4
= 16/3; μ
1
= 0; μ
2
= 2/9; μ
3
= -8/135; μ
4
= 16/135.
6.4. Равномерное распределение.
Краткие теоретические сведения.
Равномерным называется распределение вероятностей непрерывной случайной вели-
чины Х, если на интервале (а, b), которому принадлежат все возможные значения Х, плот-
ность сохраняет постоянное значение, а именно f(x) = 1/(b-a); вне этого интервала f(x) = 0.
РЕШЕНИЕ ЗАДАЧ
1. Найти математическое ожидание случайной величины Х, распределенной равно-
мерно в интервале (2,8).
Решение.
График плотности равномерного распределения симметричен относительно прямой
х=(2+8)/2 =5, поэтому М(Х) = 5.
Итак, математическое ожидание случайной величины, равномерно распределенной в
интервале (2,8) равно полусумме этого интервала.
Ответ: 5.
6.5. Нормальное распределение.
Краткие теоретические сведения.
Нормальным называют распределение вероятностей непрерывной случайной величи-
ны Х, плотность которого имеет вид
,e
2
1
)x(f
2
2
2
)ax(
σ⋅
−
−
⋅
π⋅⋅σ
=
где а - параметр, равный математическому ожиданию,
σ - параметр, равный среднему квадратическому отклонению.
Вероятность того, что Х примет значение, принадлежащее интервалу (α, β),
( )
,
aa
XP
σ
−α
Φ−
σ
−β
Φ=β<<α
где
∫
⋅⋅
π⋅
=Φ
−
x
0
2
z
dze
2
1
)x(
2
- функция Лапласа.

36
Вероятность того, что абсолютная величина отклонения меньше положительного чис-
ла δ,
Р(|X - a| < δ) = 2Ф (δ /σ).
В частности, при а =0 справедливо равенство
Р(|X < δ) = 2Ф (δ /σ).
Асимметрия, эксцесс, мода и медиана нормального распределения соответственно
равны: А
s
=0, E
k
=0, M
0
=a, где а =М(Х).
РЕШЕНИЕ ЗАДАЧ
1. Математическое ожидание и среднее квадратическое отклонение нормально рас-
пределенной случайной величины Х соответственно равны 20 и 5. Найти вероятность того,
что в результате испытания Х примет значение, заключенное в интервале (15, 25).
Решение.
Воспользуемся формулой
( )
,
aa
XP
σ
−α
Φ−
σ
−β
Φ=β<<α
Подставив α =15, β =25, а= 20 и σ =5, получим Р(15 < X <25) = Ф(1) - Ф(-1). По табли-
це приложения 2 из [1] находим: Ф(1) =0,3413. Следовательно, Р(15 < X <25) = 0,6826.
Ответ: 0,6826.

37
7. РАСПРЕДЕЛЕНИЕ ФУНКЦИИ ОДНОГО И ДВУХ СЛУЧАЙНЫХ АРГУМЕНТОВ.
7.1. Функция одного случайного аргумента.
Цель: уяснить основные определения, применение функции одного и двух случайных
аргументов в теории вероятностей.
Краткие теоретические сведения.
Если каждому возможному значению случайной величины Х соответствует одно воз-
можное значение случайной величины Y, то Y называют функцией случайного аргумента Х и
записывают Y=φ(Х).
Если Х - дискретная случайная величина и функция Y=φ(Х) монотонна, то различным
значениям Х соответствуют различные значения Y, причем вероятности соответствующих
значений Х и Y одинаковы. Другими словами, возможные значения Y находят из равенства
y
i
= φ(x
i
),
где х
i
–возможные значения Х; вероятности возможных значений Y находят из равенства
Р(Y = y
i
) = P(X = x
i
).
Если же Y=φ(Х) - немонотонная функция, то, вообще говоря, различным значениям Х
могут соответствовать одинаковые значения Y (так будет, если все возможные значения Х
попадут в интервал, в котором функция φ(Х) не монотонна). В этом случае для отыскания
вероятностей возможных значений Y следует сложить вероятности тех возможных значений
Х, при которых Y принимает одинаковые значения. Другими словами, вероятность повто-
ряющегося значения Y равна сумме вероятностей тех возможных значений Х, при которых Y
принимает одно и то же значение.
Если Х - непрерывная случайная величина, заданная плотностью распределения f(x),
и если у=φ(х) - дифференцируемая строго возрастающая или строго убывающая функция,
обратная функция которой х=ψ(у), то плотность распределения g(у) случайной величины Y
находят из равенства
g(y) = f [ψ(y)] * [ψ’(y)].
Если функция у = φ(х) в интервале возможных значений Х не монотонна, то следует
разбить этот интервал на такие интервалы, в которых функция φ(х) монотонна, и найти
плотности распределений g
i
(у) для каждого из интервалов монотонности, а затем предста-
вить g(y) в виде суммы:
g(y) = ∑g
i
(y).
Например, если функция φ(х) монотонна в двух интервалах, в которых соответст-
вующие обратные функции равны ψ
1
(у) и ψ
2
(у), то
g(y) = f [ψ
1
(y)] * |ψ
1
’(y)| + f[ψ
2
(y)] * |ψ
2
’(y)|.
РЕШЕНИЕ ЗАДАЧ
1. Дискретная случайная величина Х задана законом распределения:
X
1 3 5
P 0,4
0,1
0,5
Найти закон распределения случайной величины Y = 3⋅X.
Решение.
Найдем возможные значения величины Y=3⋅X. Имеем у
1
=3; у
2
=9; у
3
=15. Видим, что
различным возможным значениям Х соответствуют различные значения Y. Это объясняется
тем, что функция у = φ(х) = 3⋅х монотонна. Найдем вероятности возможных значений Y. Для
того, чтобы Y=у
1
=3 достаточно, чтобы величина Х приняла значение х
1
=1. Вероятность же

38
события Х =1 по условию равна 0,4; следовательно, и вероятность события Y = у
1
=3 также
равна 0,4.
Аналогично получим вероятности остальных возможных значений Y:
Р(Y = 9) = P (X = 3) = 0,1;
P(Y = 15) = Р (Х = 5) = 0,5.
Напишем искомый закон распределения Y:
Ответ:
Y
3 9 15
P 0,4
0,1
0,5
2. Задана плотность распределения f(x) случайной величины Х, возможные значения
которой заключены в интервале (a,b). Найти плотность распределения случайной величины
Y = 3⋅Х.
Решение.
Так как функция у = 3⋅х дифференцируемая и строго возрастает, то применима фор-
мула
g(y) = f [ψ(y)] * [ψ ' (y)], (*)
где ψ(y) - функция, обратная функция у = 3⋅х.
Найдем ψ(y):
ψ(y) = х = у/3.
Найдем f [ψ(y)]:
f [ψ(y)] = f (у/3). (**)
Найдем производную ψ’(y):
ψ ' (y) = (у/3) ' = 1/3.
Очевидно, что
| ψ ' (y)| = 1/3. (***)
Найдем искомую плотность распределения, для чего подставим (**) и (***) в (*):
g(y) = (1/3) f ' (y/3).
Так как х изменяется в интервале (а, b) и у= 3⋅х, то 3a < y < 3b.
Ответ: g(y) = (1/3) f ' (y/3).
3. Задана плотность распределения f(x) случайной величины Х, возможные значения
которой заключены в интервале (0, ∞). Найти плотность распределения g(y) случайной вели-
чины Y, если: а) Y= е
–х
; б) Y =ln(X); в) Y= Х
3
; г) Y=1/Х²; д) Y=
Х
.
Решение.
а) Применим формулу
g(y) = f [ψ(y)] * [ψ ' (y)],
Найдем ψ(y):
ψ(y) = х = ln (y).
Найдем f [ψ(y)]:
f [ψ(y)] = f [ln (y)]. (**)
Найдем производную ψ ' (y):
ψ ' (y) = [ln(у)] ' = 1/y.
Очевидно, что
| ψ ' (y)| = 1/y. (***)
Найдем искомую плотность распределения:
.
y
1
lnf)yln()y(g
⋅=
Так как х изменяется в интервале (0, ∞) и Y= е
–х
, то (0< y< 1).
Аналогично найдем плотности распределения для остальных вариантов:
б) );y(- ],e[fe)y(g
yy
+∞<<∞⋅=
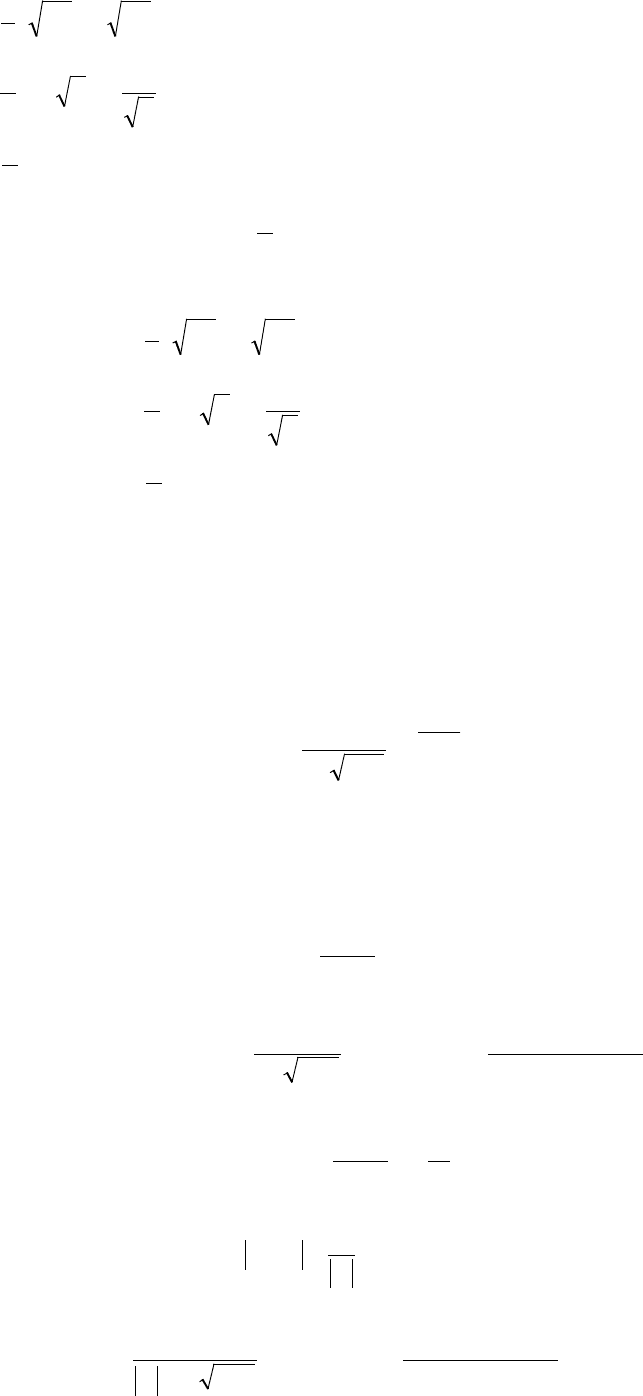
39
в) );y(0 ,yfy
3
1
)y(g
3
2
3
2
+∞<<
⋅⋅=
г) );y(0 ,
y
1
fyy
2
1
)y(g +∞<<
⋅⋅⋅=
д)
[
]
).y(0 ,yfy
2
1
)y(g
2
+∞<<⋅⋅=
Ответ: а)
.
y
1
lnf)yln()y(g
⋅=
б)
[
]
);y(- ,efe)y(g
yy
+∞<<∞⋅=
в) );y(0 ,yfy
3
1
)y(g
3
2
3
2
+∞<<
⋅⋅=
г) );y(0 ,
y
1
fyy
2
1
)y(g +∞<<
⋅⋅⋅=
д)
[
]
).y(0 ,yfy
2
1
)y(g
2
+∞<<⋅⋅=
4. Случайная величина Х распределена нормально с математическим ожиданием, рав-
ным а, и среднеквадратическим отклонением, равным σ. Доказать, что линейная функция Y
= A·X + B также распределена нормально, причем
М(Y) = A·a + B, σ(Y) = |A|·σ.
Решение.
Напишем плотность распределения случайной величины Х:
.е
2
1
)x(f
2
2
2
)ax(
σ⋅
−
−
⋅
π⋅⋅σ
=
Функция у = Ах +В монотонна, поэтому применима формула
g(y) = f [ψ(y)] · |ψ ' (y)|. (*)
Найдем х = ψ(y) из уравнения у = А·х + В:
.
A
By
)y(
−
=ψ
Найдем f [ψ(y)]:
[ ]
[
]
( )
.
A2
B)a(A-y
p где ,e
2
1
)y(f
2
2
p
σ⋅⋅
+⋅
=⋅
π⋅⋅σ
=ψ
−
(**)
Найдем ψ '(y):
.
A
1
A
By
)y('
'
=
−
=ψ
Найдем |ψ ' (y)|:
.
A
1
)y(' =ψ | (***)
Подставляя (**) и (***) в (*), имеем
[
]
( )
.
A2
B)a(A-y
p где ,e
2A
1
)y(g
2
2
p
σ⋅⋅
+⋅
=⋅
π⋅⋅σ⋅
=
−

40
Отсюда видно, что линейная функция Y = A·X + B распределена нормально, причем
M(Y) = A·a + B и σ(Y) = |A|·σ, что и требовалось доказать.
Ответ: функция Y = A·X + B распределена нормально, причем M(Y) = A·a + B и
σ(Y) = |A|·σ, что и требовалось доказать.
7.2. Функция двух случайных аргументов.
Краткие теоретические сведения.
Если каждой паре возможных значений случайных величин Х и Y соответствует одно
возможное значение случайной величины Z, то Z называют функцией двух случайных аргу-
ментов X и Y и пишут
Z = φ(X,Y).
Если Х и Y - дискретные независимые случайные величины, то, для того, чтобы найти
распределение функции Z=X+Y, надо найти все возможные значения Z, для чего достаточно
сложить каждое возможное значение X со всеми возможными значениями Y; вероятности
найденных возможных Z равны произведениям вероятностей складываемых значений X и Y.
Если Х и Y - непрерывные независимые случайные величины, то плотность распреде-
ления g(z) суммы Z=X+Y (при условии, что плотность распределения хотя бы одного из ар-
гументов задана в интервале (-∞, ∞) одной формулой) может быть найдена по формуле:
∫
+∞
∞
−
⋅−⋅= ,dx)xz(f)x(f)z(g
21
либо по равносильной формуле
∫
+∞
∞
−
⋅−⋅= ,dy)yz(f)y(f)z(g
12
где f
1
и f
2
–плотности распределения аргументов; если возможные значения аргументов не-
отрицательны, то плотность распределения g(z) величины Z=X+Y находят по формуле:
∫
⋅−⋅=
z
0
21
,dx)xz(f)x(f)z(g
либо по равносильной формуле
∫
⋅−⋅=
z
0
12
.dy)yz(f)y(f)z(g
В том случае, когда обе плотности f
1
(х) и f
2
(х) заданы на конечных интевалах, для
отыскания плотности g(z) величины Z=X+Y целесообразно сначала найти функцию распре-
деления G(z), а затем продифференцировать ее по z:
g(z) = G’(z).
Если Х и Y - независимые случайные величины, заданные соответствующими плот-
ностями распределения f
1
(х) и f
2
(х), то вероятность попадания случайной точки (Х,Y) в об-
ласть D равна двойному интегралу по этой области от произведения плотностей распределе-
ния:
(
)
[
]
.dydx)y(f)x(fDY,XP
21
∫∫
⋅⋅⋅=⊂
РЕШЕНИЕ ЗАДАЧ
1. Дискретные независимые случайные величины Х и Y заданы распределениями:
X
1 3 Y
2 4
P 0,3
0,7
P 0,6
0,4
Найти распределение случайной величины Z = X +Y.
