Зимина О.В., Кириллов А.И., Сальникова Т.А. Высшая математика. Решебник

Подождите немного. Документ загружается.

30 Гл. 1, Аналитическая геометрия

Подставляя в параметрические уравнения прямой найденное

значение to = 1, получаем

2^0 = 3, 2/0 = -1,

= -1.

Ответ. Прямая и плоскость пересекаются в точке (3,-1,-1).

Условия ЗАДАЧ. Найти точку пересечения прямой и плоскости,

^ х-2 у-3

+ 1

1 1 -4

x +

y~\-2z-9

= 0.

х + 1 ty-3

+ 1

-^ = У-^ = -^, :,^2y-z + b = 0.

X —

1 _ у -ЬЬ _ Z

—

1 "" 4 " 2 '

х-Зг/+ 2-8 = 0.

х-1

у z-{-3

- = ^ = -^, 3a; + y-2z-0.

6. ^ = ^ = ^, x + 3y-z-3 = 0.

Ж —

1 V

—

2 z

8. -^ = ^ = -, X-2/ + 4Z-5-0.

9. £ =

Lzi.£±f,

2x-y + z + 4 = 0.

10.

^ = ^ = i±l, 2x-4,-3z + 7 = 0.

Ответы. 1. (1,2,3). 2. (1,-1,4). 3. (2,-1,3). 4. (4,0,-1).

5.(1,1,2). 6. (-1,0,-4). 7. (-1,1,-2). 8.(3,2,1). 9. (-1,-1,-3).

10.

(-1,2,-1).

1.12. Проекция точки на плоскость или прямую 31

1-12. Проекция точки

на

плоскость или прямую

ПОСТАНОВКА

ЗАДАЧИ. Найти координаты проекции Р' точки

P{^PiУРЧzp)

па плоскость Ах + By

-\-

Cz-\- D = О,

ПЛАН

РЕШЕНИЯ. Проекция Р' точки Р на плоскость является ос-

нованием перпендикуляра, опущенного из точки Р на эту плоскость.

Составляем уравнения прямой, проходящей через точку Р пер-

пендикулярно данной плоскости. Для этого в качестве направляю-

щего вектора прямой берем нормальный вектор плоскости: а = п =

= {А, В, С}. Тогда канонические уравнения прямой имеют вид

х-хр

у-ур Z- zp

А В С '

Находим координаты точки пересечения Р' этой прямой с за-

данной плоскостью (см. задачу

1.11).

Положим

х-хр

_ у-ур _ Z-

~ В ~ С "

Тогда параметрические уравнения прямой имеют вид

= At-\- хр,

у = Bt-\-yp,

Ct-\- Zp.

Подставляя x^y^z в уравнение плоскости и решая его относи-

тельно t, находим значение параметра t = to, при котором происходит

пересечение прямой и плоскости.

Найденное значение ^о подставляем в параметрические уравне-

ния прямой и получаем искомые координаты точки Р'.

ЗАМЕЧАНИЕ.

Аналогично решается задача о нахождении коорди-

нат проекции точки на прямую.

ПРИМЕР.

Найти координаты проекции Р' точки Р(1,2,—1) на

плоскость Зж

—

2/4-22:

—

4 = 0.

РЕШЕНИЕ.

Составляем уравнения прямой, проходящей через точку Р пер-

пендикулярно данной плоскости. Для этого в качестве направляю-

щего вектора прямой берем нормальный вектор плоскости: а = п =

32 Гл.

Ансиитическая геометрия

= {3,

—1,2}.

Тогда канонические уравнения прямой имеют

вид

х-1

_ у-2 _ z-hl

"" -1 2 '

Найдем координаты ТОЧЮЙ пересечения

Р'

этой прямой

задан-

ной плоскостью. Положим

х-~1

__ у-2 __

"" -1 •" 2 "^ '

Тогда параметрические уравнения прямой имеют

вид

x^St

+ 1,

= -t + 2,

= 2t - 1.

Подставляя

эти

выражения

для

х^

у и z в

уравнение плоскости,

находим значение параметра ^,

при

котором происходит пересечение

прямой

плоскости:

3(3t

+ 1) - l{-t +

2{2t

- 1) -

=> to = 2.

Подставляя

параметрические уравнения прямой найденное

значение

to = 2,

получаем жо

= 7, уо =

О,

^о = 1.

Таким образом, точка пересечения прямой

плоскости

и,

следо-

вательно, проекция точки

Р на

плоскость имеет координаты (7,0,1).

Ответ. Проекция

Р'

имеет координаты (7,0,1).

Условия ЗАДАЧ.

Р(1,0,1),

Р(-1,0,-1),

Р(2,1,0),

Р(0,2,1),

Р(-1,2,0),

6. Р(2,-1,1),

Р(1,1,1),

8. Р(1,2,3),

9. Р(0,-3,-2),

10.

Р(1,0,-1),

Найти координаты проекции точки

4х

бу

-f 4z -

= 0.

2х + 6у'-2г-\-11 = 0.

2/-hz

= 0.

2а:

42/

- 3 = 0.

4х-52/-г-7

= 0.

x-y-\-2z-2=^0.

ж-f-42/+

З2:

4-5 = 0.

2х -h Юу

lOz

= 0.

2х -МО2/

-f-

lOz

- 1 = 0.

+ 4z-l = 0.

на

плос-

Ответы.

1.(2,3/2,2).

2. (-3/2,-3/2,-1/2). 3.(2,-1/2,-3/2).

(-1/2,1,1). 5.(1,-1/2,-1/2). 6.(3/2,-1/2,0). 7.(1/2,-1,-1/2).

8.(1/2,-1/2,1/2). 9.(1/2,-1/2,1/2). 10.(1,1/2,0).

1.13. Симметрия относительно прямой или плоскости 33

1.13. Симметрия относительно

прямой или плоскости

ПОСТАНОВКА ЗАДАЧИ. Найти координаты точки Q, симметрич-

ной точке P{xp,yp,zp) относительно прямой

- хр _ у -уо _ Z -

I т п

ПЛАН РЕШЕНИЯ. Искомая точка Q лежит на прямой, перпенди-

кулярной данной и пересекающей ее в точке Р'. Поскольку точка

Р'

делит отрезок PQ пополам, координаты жд, уд и ZQ

ТОЧКИ

определяются из условий

хрЛ-XQ yp + yq zp +

^Р' = 2"^, УР' = 2~^. ^Р' = ^, (1)

где xp,yp,zp — координаты точ1си Р и xp^^ypf^zp/ — координаты

ее проекции Р' на данную прямую.

Найдем проекцию точки Р на данную прямую, т.е. точку Р'

(см.

задачу

1.12).

Для этого:

а) составим уравнение плоскости, проходящей через точку Р пер-

пендикулярно данной прямой. В качестве нормального вектора п

этой плоскости можно взять направляющий вектор данной прямой,

т.е.

п = а = {l^m^n}. Получаем

1{х - Хр) + т{у - УР) -f n{z - zp) = 0;

б) найдем координаты точки пересечения Р' этой плоскости с за-

данной прямой. Для этого запишем уравнения прямой в параметри-

ческой форме

= Н-\- жо,

y = mt-\-yo,

Z = nt-\- ZQ.

Подставляя x^y^z в уравнение плоскости и решая его относительно t,

находим значение параметра t = to, при котором происходит пересе-

чение прямой и плоскости;

в) найденное значение to подставляем в параметрические уравне-

ния прямой и получаем искомые координаты точки Р'.

Координаты точки Q, симметричной точке Р относительно дан-

ной прямой, определяем из условий (1). Получаем

XQ = 2хр/ - Хр, yq = 2ур' - ур, ZQ = 22;р/ - zp.

34 Гл.

Аналитическая геометрия

ЗАМЕЧАНИЕ. Аналогично решается задача о нахождении коорди-

нат точки, симметричной данной, относительно плоскости.

ПРИМЕР. Найти координаты точки Q, симметричной точке

Р(2,

-1,2) относительно прямой

X —

1 _ у

__ Z

-\-1

1 "^ О -2 *

РЕШЕНИЕ.

Найдем проекцию точки Р на данную прямую, т.е. точку Р'.

Для этого:

а) составим уравнение плоскости, проходящей через точку Р пер-

пендикулярно данной прямой. В качестве нормального вектора п

этой плоскости можно взять направляющий вектор данной прямой:

n = a =

{1,0,-2}.

Тогда

1(а: - 2) + 0(2/ + 1) - 2(z - 2) =

=Ф

- 2z + 2 = 0;

б) найдем точку пересечения заданной прямой и плоскости

—

2z + 2 = 0. Для этого запишем уравнения прямой в парамет-

рической форме:

x = t + l,

z = -2t- 1.

Подставляя эти выражения для х, у и z в уравнение плоскости, на-

ходим значение параметра t, при котором происходит пересечение

прямой и плоскости: to =

—1;

в) подставляя в параметрические уравнения прямой найденное

значение to =

—1,

получаем

жр/

О,

г/р/ =

О,

zpr = 1.

Таким образом, точка пересечения прямой и плоскости и, следова-

тельно, проекция точки Р на прямую есть Р'(0,0,1).

Координаты точки Q, симметричной точке Р относительно дан-

ной прямой, определяются из условий (1):

XQ = 2хр'

—

Хр = —2,

VQ = 2ур/ - 2/р = 1,

= 2zpf

—

zp = 0.

Ответ. Точка Q имеет координаты (—2,1,0).

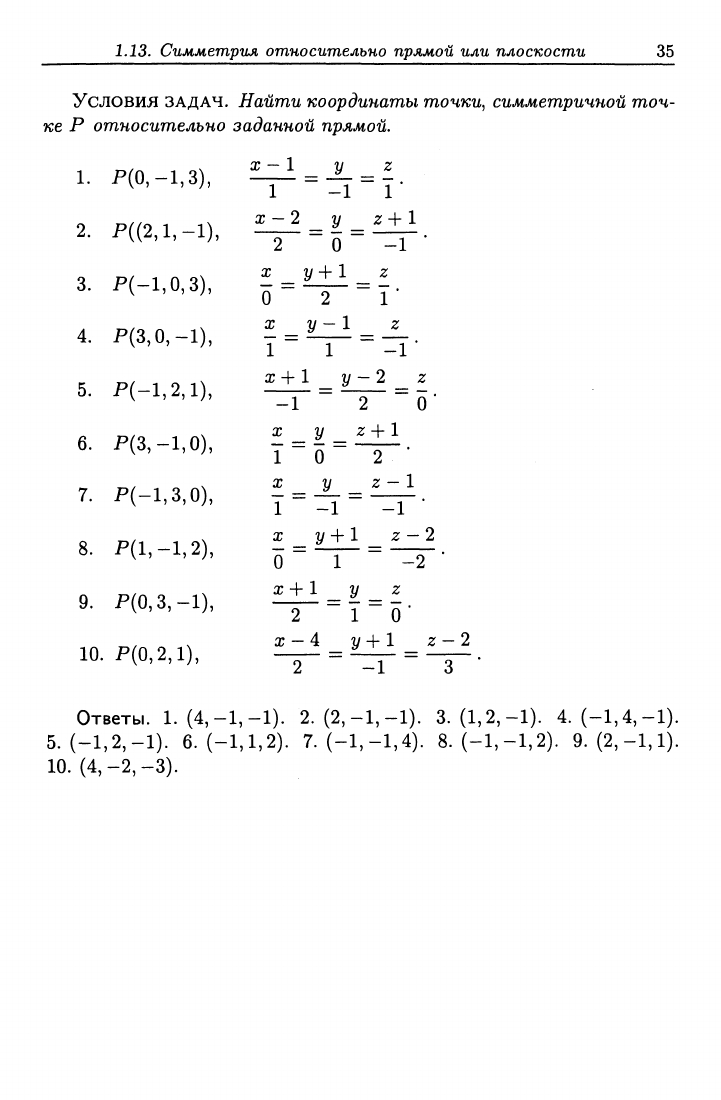
1.13. Симметрия относительно прямой или плоскости 35

Условия ЗАДАЧ. Найти координаты точки, симметричной точ-

ке Р от^носителъно заданной прямой.

Р(0,-1,3),

Р((2,1,-1),

Р(-1,0,3),

Р(3,0,-1),

Р(-1,2,1),

6. Р(3,-1,0),

Р(-1,3,0),

8. Р(1,-1,2),

9. Р(0,3,-1),

10.Р(0,2,1), 2-13-

Ответы.

1.(4,-1,-1).

2.(2,-1,-1). 3.(1,2,-1). 4. (-1,4,-1).

(-1,2,-1). 6. (-1,1,2). 7. (-1,-1,4). 8. (-1,-1,2). 9.(2,-1,1).

10.(4,-2,-3).

X —

0 '

Т''

1 _ 2/ .

-1 "

+ 1 _

_2/-1.

х +

1 __

у -

-1 - ~

_У _ ^

~ 0 ~

_ 2^ _

-1

+ 1

+ 1 _ 2/

2 1

-4 _ у_

-1 *

' 1

-2 _z

+ 1

г-1

-1

_ Z-2

-2 '

+ 1 _ 2^-2

Глава 2

ЛИНЕЙНАЯ АЛГЕБРА

При изучении темы ЛИНЕЙНАЯ АЛГЕБРА вы познакомитесь на

примерах с понятиями линейного (векторного) пространства, линей-

ного оператора, его матрицы, образа, ядра, ранга, дефекта, собствен-

ных векторов и собственных значений. Вы научитесь выполнять раз-

личные операции с операторами и матрицами, исследовать и решать

системы линейных уравнений, получать всю информацию об опера-

торе (матрицу, образ, ядро, ранг и дефект, собственные векторы и

собственные значения) по его матрице, преобразовывать векторы и

матрицы при изменениях базисов.

С помощью пакета РЕШЕБНИК.ВМ вы можете выполнить все

действия с матрицами, привести матрицу к редуцированному (га-

уссову) виду, вычислить определители, обратную матрицу, решить

системы уравнений, проверить линейность оператора, решить харак-

теристическое уравнение, найти собственные векторы и собственные

значения оператора, выполнить все численные расчеты и проверить

правильность полученных вами результатов.

2.1,

Правило Крамера

ПОСТАНОВКА ЗАДАЧИ. Решить систему трех линейных уравне-

ний с тремя неизвестными

СЦХХ

+ С12Х2 -Ь СхзЖз = ^1,

C2ia:i + C22X2 + С23Х3 = d2,

Csia^l -Ь CS2X2 + СззХз = ^3

по правилу Крамера.

ПЛАН РЕШЕНИЯ. ЕСЛИ определитель матрицы системы

Д =

СЦ С12 С13

С21 С22 С23

С31 Сз2 Сзз

2.1.

Правило Крамера

отличен от нуля, то система имеет решение и притом только одно.

Это решение определяется формулами

^'~ д'

г = 1,2,3,

(1)

где Ai - определитель матрицы, получаемой из матрицы системы

заменой г-ого столбца столбцом свободных членов.

Вычисляем определитель матрицы системы

СЦ

CI2 CI3

С21 С22 С23

С31 Сз2 Сзз

И убеждаемся, что он не равен нулю. Следовательно система уравне-

ний имеет единственное решение.

Вычисляем определители

Ai:

dl Ci2 Ci3

d2 C22 C23

6^3 С32 Сзз

Сц dl ci3

C21 d2 C23

сз1

ds Сзз

Сц Ci2 dl

C21 C22 C?2

C31 C32 ds

По формулам Крамера (1) находим решение системы уравнений

Х2 =

хз =

А •

ПРИМЕР. Решить систему уравнений

XI +

2ж2

+ а:з = 4,

Зжх

—

5x2 + Зхз = 1,

2^1 + 7^2 - жз = 8

по правилу Крамера.

РЕШЕНИЕ.

Вычисляем определитель матрицы системы, разлагая его по

первой строке:

-5

1-(-16)-2-(-9)+

1-31 = 33.

Так как он не равен нулю, то система уравнений имеет единственное

решение.

Гл.

2. Линейная алгебра

Вычисляем определители

4 2 1

1 -5 3

] 7 -1

= 4-(-16)-2. 25 +1-47 = 33,

До =

Дя =

1 4 1

3 1 3

2 8-1

1 2 4

3 -5 1

2 7 8

(-25) - 4

(-9) -h 1

•

22 = 33,

= 1. (-47) - 2

•

22 + 4

31 = 33.

По формулам Крамера (1) находим решение системы уравнений

XI =1, Х2 = 1, Жз = 1.

Ответ, xi = 1,

Ж2

= 1, жз = 1.

Условия ЗАДАЧ

мера.

i 2х

Зх

2х

3. I Зх

Бх

Решить системы уравнений по правилу Кра-

2х

Ъх

Зж

2х

Ъх

2х

Ответы.

3. XI

Х2

+ Ъх2 -

а:з

= 2,

- Зж2

-f

2жз = О,

- 2^2 - жз = 4.

Н-

3x2

+ хз = 1,

- 5x2 + 2хз = -И,

2x2

- 2x3 = -3.

Н-

5x2

+ хз = -8,

- 3x2 + 5хз = 16,

-f 2x2

а^з

= -6.

2X2

а;з

= 2,

2x2 -f

Зхз = б,

- 2x2 - хз = 7.

+ 3x2 + хз = —5,

- 4x2 + Зхз = 11,

10.

-f 2x2 -Ь

хз = 5,

3xi — 5x2

~i~

Зхз =

—7,

2xi

-f

7x2 — Хз = 13.

xi +

4x2 -Ь

Зхз = 5,

3xi — 2x2 + Зхз = 9,

2xi +

4x2

— Зхз = 1.

xi +

3x2

+ 2хз = —5,

2x1 - 2x2 + 3x3 = -8,

3xi

-f-

4x2

- 4x3 = 5.

Xi +

5X2

+ Хз = 3,

2xi — 3x2 + Зхз = 8,

2xi +

4x2

- Хз = 0.

xi +

2x2

+ Зхз = 5,

3xi — 2x2 + Зхз = —1,

2xi

3x2

- 2хз = 8.

-f 4x2

- Хз = -9.

vyiDc.D.. 1. Xi = 1, X2 =

Хз =

-1.

2. Xi = 0, X2 =

Хз = 1.

xi =

-1,

X2 =

Хз =

4. xi =r

X2 =

Хз = 1. 5. xi = 0,

-2,

Хз =

6. xi =

-1,

X2 =

Хз =

-2.

xi =

X2 = 0,

„^ =

-1.

8. xi = 1, X2 = 0, Хз = 2. 9. xi = 0, X2 =

-2,

хз = 1.

10.

xi =

X2 =

Хз = 0.

2.2.

Обратная матрица 39

2.2.

Обратная матрица

ПОСТАНОВКА ЗАДАЧИ. Задана квадратная матрица т^ретьего

порядка

(

Си С12 С13

С21 С22 С23

С31 С32 Сзз

Установить существование и найти обратную матрицу С~^.

ПЛАН РЕШЕНИЯ. Матрица С~^ называется обратной квадратной

матрице С, если

где Е — единичная матрица.

Если detC ф О (матрица С — невырожденная), то матрица С

имеет обратную, если det С = О, то матрица С не имеет обратной.

Вычисляем определитель матрицы det С Если det С ^ О, то

матрица С имеет обратную.

Составляем матрицу из алгебраических дополнений

Транспонируем матрицу С

Разделив матрицу С^ на определитель, получаем искомую об-

ратную матрицу

Си С21 Сз1

Си С22 Сз2

Си

С21

Сз1

хуС

Си

С\2

C\z

С\2

С22

Сз2

С 21

С22

С23

Ci3

C2Z

С'зз

с31

Сз2

Сзз

det с \ ^ ^ г*

<-^13 ^2Z <~^33

Проверяем, что С

•

С~^ = Е и записываем ответ.

ПРИМЕР. Задана квадратная матрица третьего порядка

С= I 3 -5