Зоценко Н.Л. Инженерная геология. Механика грунтов, основания и фундаменты

Подождите немного. Документ загружается.

150

тимих для нормальної експлуатації, а їх несуча здатність має бути достатньою,

щоб не виникла втрата стійкості чи руйнування основи.

Закордонні норми проектування основ, хоч і не базуються на принципах

граничних станів, але, починаючи з формули К. Терцагі з уточненнями Мейєр-

гофа, Како-Керізеля, Хансена та інших, містять вирази, до складу яких входять

емпіричні коефіцієнти i, λ, d, N, що залежать від кута внутрішнього тертя φ.

У 70-ті роки з’явились пропозиції перейти до проектування основ, вихо-

дячи з положень сучасної теорії надійності (М. М. Єрмолаєв і В. В. Міхєєв –

1976; А. П. Пшеничкін – 1980; В. Б. Швець й інші – 1980; О. В. Школа – 1980;

О. І. Ігнатова – 1982; М. М. Кризський – 1987; Б. П. Макаров і Б. Ю. Кочетков –

1987; Г. Б. Кульчицький – 1990 та інші), котра є подальшим розвитком принци-

пу граничних станів. Надійність оцінюють імовірністю того, що протягом усьо-

го періоду експлуатації споруди не виникне стан основи, що загрожує її екс-

плуатації. Цей підхід розглянуто в розділі 19. Він дає більш економічні рішен-

ня, але вимагає переходу на статистичні методи розрахунків, які зараз лише ап-

робуються.

Тепер при проектуванні найчастіше застосовують роздільний розрахунок

основ і споруд. Спочатку розраховують будівлю й визначають навантаження,

що передаються на основу так, наче вона абсолютно жорстка та неподатлива.

Потім за цими зусиллями, користуючись спрощеними нормативними правила-

ми, визначають деформації фундаментів, які порівнюють з гранично допусти-

мими.

Повне використання переваг принципу граничних станів можливе з пере-

ходом на методику сумісного розрахунку роботи основи, фундаментів і споруд

у цілому, в результаті котрої відбувається перерозподіл зусиль, що діють на ма-

сив ґрунту (С. М. Клепіков – 1987, 1996). При цьому бажано врахувати просто-

рову роботу конструкцій, геометричну та фізичну нелінійність, анізотропність,

пластичні й реологічні властивості матеріалів і ґрунтів, можливості зміни їх

властивостей у процесі зведення (включаючи технологію та послідовність зве-

дення споруд, а також темпи і графік будівництва) й експлуатації споруд.

Залучення цих чинників до вихідних даних наближає прогноз напружено-

деформованого стану основи до дійсності. Так, при проектуванні об’єктів по

етапах: відривання котловану; зведення фундаментів і підземної частини буді-

влі; зміна рівня ґрунтових вод; будівництво надземної частини; експлуатація

споруди – встановлено, що зусилля в конструкціях зростають у кілька разів і

можуть змінювати свій знак на протилежний. При цьому повною мірою врахо-

вуються варіантність як конструктивного, так і технологічного рішення зведен-

ня споруд, у тому числі чинника часу, а також деформування прилеглої терито-

рії та навколишніх будівель. Звідси можлива оптимізація технології зведення

споруд.

Сучасні задачі механіки ґрунтів дуже різноманітні й мають практичну

спрямованість, зокрема: визначення напруг у ґрунтовій товщі; розрахунок де-

формацій і прогноз осідань фундаментів інженерних споруд; знаходження не-

сучої здатності елементів ґрунтового масиву (навколо фундаментів, паль, пі-

дземних споруд); визначення тиску ґрунтів і гірських порід на підпірні стіни й

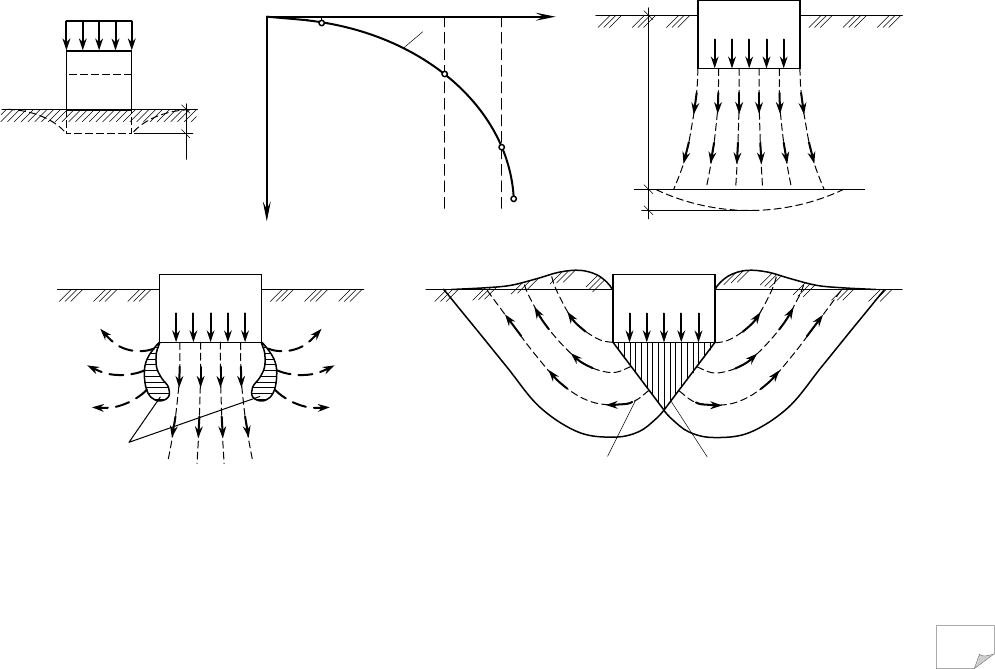
151

інші огороджуючі споруди; розрахунок стійкості укосів; прогнозування дефор-

мацій при утворенні підземних виробок, підтопленні, морозному випинанні, пі-

дземних вибухах тощо. Їх розв’язання засобами механіки ґрунтів неможливе

без широкого використання досягнень теорій пружності, пластичності, повзу-

чості, гідромеханіки, механіки руйнування, математичної фізики й ін. Такі за-

дачі зараз вирішуються, як правило, лише числовими методами із застосуван-

ням сучасних комп’ютерів (про це більш докладно див. п.п. 10.4, 10.5).

6.2. ФАЗИ НАПРУЖЕНОГО СТАНУ ҐРУНТУ

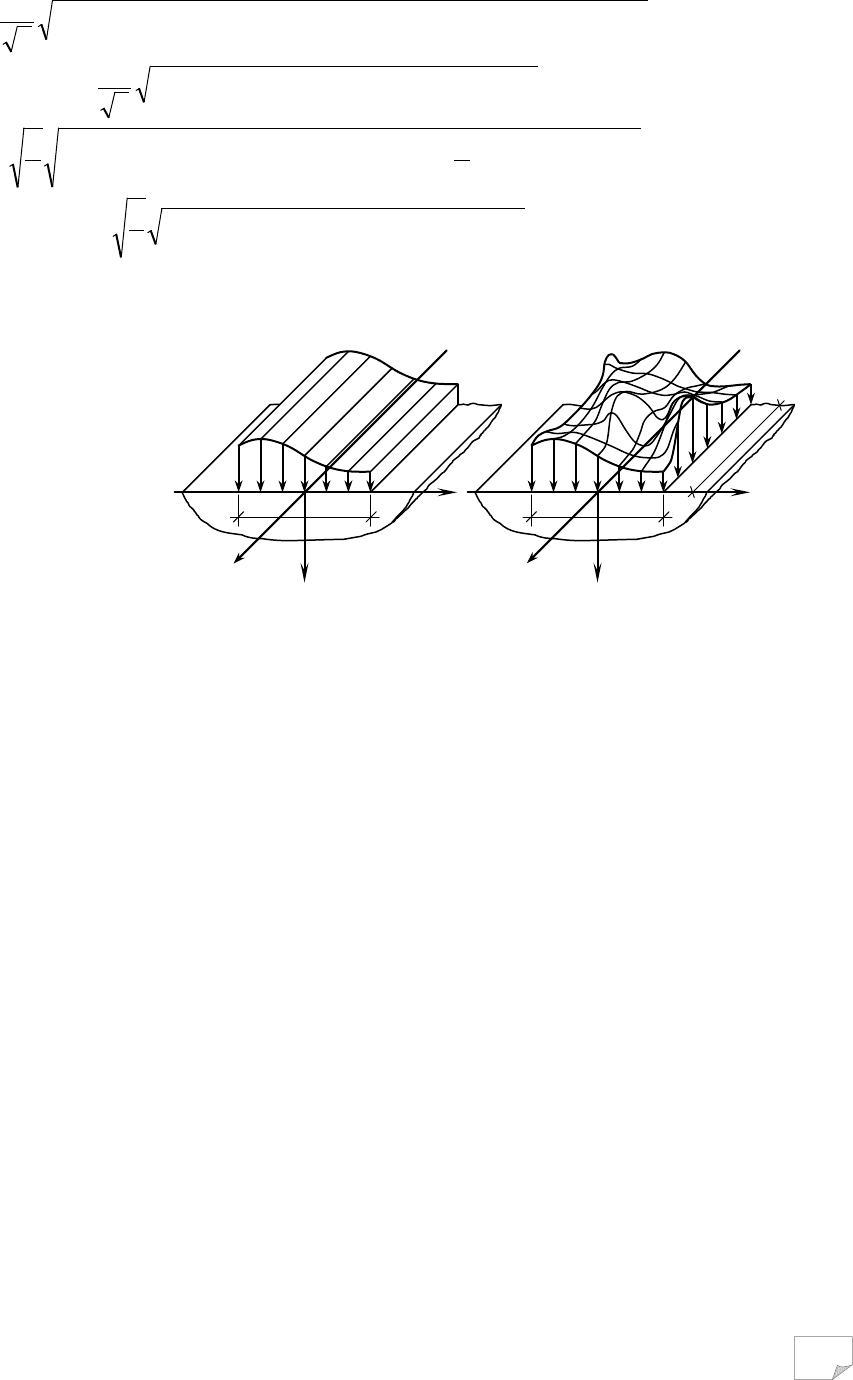
Розглянемо процес деформації масиву ґрунту від дії на нього місцевого

зростаючого навантаження. Для цього на поверхні ґрунту, що має структурну

міцність, розмістимо жорсткий штамп (чи фундамент), за підошвою якого на

ґрунт передається зростаючий тиск σ (рис. 6.1, а). Під його дією відбувається

переміщення поверхні ґрунту (осідання штампа S), величина якого зростає із

збільшенням σ. Зразу зазначимо, що ґрунт при цьому відчуває складний напру-

жений стан, який суттєво відрізняється від компресійного стиснення, бо ґрунт,

крім нормальних, відчуває й дотичні напруги, які при досягненні певної вели-

чини можуть викликати незворотні зрушення.

До речі, ще наприкінці XIX сторіччя професор В. І. Курдюмов шляхом

фотографування процесу вдавлювання штампу в лотку з прозорою передньою

стінкою визначив траєкторії переміщень часток основи і форму ліній ковзання

при втраті стійкості піщаними ґрунтами. Надалі ці дослідження продовжили

В. Г. Березанцев, С. С. Голушкевич, М. В. Малишев, В. В. Соколовський та ін-

ші.

Рис. 6.1. Схема розвитку деформацій ґрунтового масиву від дії місцевого зростаючого

навантаження: а – випробування ґрунту штампом; б –

графік залежності його осідання

від тиску за підошвою; в – фаза ущільнення та місцевих зрушень ґрунту; г – фаза роз-

витку інтенсивних деформацій зрушень і ущільнення; д – фаза випинання ґрунту;

1 – зона зсувів; 2 – лінії ковзання; 3 – ущільнене ядро

str

III

Δh

152

На рис. 6.1, б наведена крива деформації ґрунту від дії місцевого посту-

пово зростаючого навантаження S=f(σ). На ній можна виділити три ділянки

(фази): oa, ab, bc. Поки зовнішній тиск не перевищив структурну міцність ґрун-

ту σ

str

, він відчуває незначні, переважно пружні, деформації. За межею σ

str

під

штампом виникає ущільнення ґрунту за рахунок зменшення його пористості. Із

збільшенням навантаження, ґрунт ущільнюється в усе більшій зоні (це показано

на рис. 6.1, в). Вплив дотичних напруг τ поки що ледь помітний. Частинки ґрун-

ту рухаються вниз із незначним відхиленням убік від вертикалі. Зона перемі-

щень (деформацій) ґрунту поширюється на значну глибину, як правило, значно

більшу за ширину штампа (фундаменту). Чим вища щільність ґрунту, тим на

більшій глибині спостерігають рух частинок. На графіку деформації ґрунту

S=f(σ) цей етап відповідає ділянці oa. Залежність між тиском на ґрунт і осідан-

ням штампу лінійна. Одночасно в ґрунті під краями штампа, де виникає кон-

центрація напруг, розвиваються пластичні деформації (деформації зрушень).

Графік S=f(σ) починає набувати криволінійності. Та все ж при відносно невели-

кому тискові, що звичайно виникає під підошвою фундаментів будівель, цей

графік можна наближено прийняти за пряму. Таку фазу напруженого стану ос-

нови називають фазою ущільнення та місцевих зрушень ґрунтів.

Із точки зору міцності ґрунту ця фаза – безпечна, бо ґрунт набуває більш

щільної структури, а осідання носять відверто згасаючий у часі характер. У

практичних розрахунках у її межах залежність S=f(σ) приймають лінійною. Це

дає змогу застосовувати для розрахунків напруг і визначення кінцевих осідань

у фазі ущільнення теорію лінійно деформованого середовища. Тиск, що відпо-

відає межі між фазами I і II, називають першим критичним тиском.

Подальше збільшення навантаження на штамп призводить до розвитку

зон пластичних деформацій у боки й ущільнення ґрунтів навколо цих зон (як це

показано на рис. 6.1, г). Зони зрушення поступово поширюються, охоплюючи

все більший простір. Ця фаза напруженого стану основи отримала назву фази

розвитку інтенсивних деформацій зрушень та ущільнення. На графіку S=f(σ) їй

відповідає криволінійна ділянка ab. Деякі площадки зрушень, що виникають

протягом цієї фази, поступово з’єднуються, утворюючи під навантаженим шта-

мпом суцільну поверхню ковзання.

Як показали досліди В. Г. Березанцева та В. О. Ярошенка, ущільнене ядро

(див. рис. 6.1, д), котре почало утворюватись під штампом у двох перших фа-

зах, повністю формується із досягненням ґрунтом максимальної несучої здат-

ності. Надалі ядро залишається незмінним. Воно рухається разом із штампом,

працюючи як клин, розсуваючи ґрунт в боки й зумовлює значні осідання штам-

па. Тиск, що відповідає межі між фазами II і III, називають другим критичним

тиском або межею міцності чи межею несучої здатності основи.

Нарешті, під дією деякого тиску відбувається різке осідання штампа з ви-

пинанням ґрунту в боки та нагору. На кривій S=f(σ) з’являється майже вертика-

льна ділянка bc, що відповідає фазі випинання (руйнування) ґрунту. При цьому

напруженому стані переважають: бічні зміщення часток, розвиток суцільної по-

верхні ковзання, втрата стійкості товщі ґрунту (як це показано на рис. 6.1, д).

На практиці фаза випинання звичайно виникає раптово і має катастро-

153

фічний характер. Відбувається руйнування основи, фундамент та надземні

конструкції зазнають аварійних деформацій. У багатьох випадках при ексцент-

ричному прикладанні навантаження відбувається частковий поворот фундамен-

ту та зміщення його вбік. Для великих ексцентриситетів можливе однобічне

випирання ґрунту на поверхню і значний крен споруди. Класичним випадком

цієї фази напруженого стану основи є аварія Трансконського елеватора в Канаді

(рис. 6.2).

Розглянемо й важливе для

практики питання залежності осі-

дання від розмірів штампа. На гра-

фіку залежності осідання від роз-

мірів штампа при однаковому тис-

кові (рис. 6.3) В. О. Вєсєлов виді-

лив три ділянки: першу для малих

штампів площею А≤400 см

– де-

формація відбувається переважно за рахунок випирання ґрунту з-під штампа;

другу для штампів площею А=400-2000 см

; третю для штампів площею А≥2000

см

– деформації зумовлені, головним чином, ущільненням ґрунтів. Для штам-

пів площею до 10-15 м

, а іноді й більше на третій ділянці осідання можна вва-

жати пропорційним площі фундаменту.

Якщо в межах третьої ділянки процес руйнування ґрунту під вузьким і

широким фундаментами прийняти однаковим, то міцність основи останнього

буде більшою, бо в процес зрушень залучається більший об’єм ґрунту, й крити-

чному тискові буде відповідати більша величина абсолютного осідання.

6.3. ОСНОВНІ ПОЛОЖЕННЯ ПРО РОЗПОДІЛ НАПРУГ І

ДЕФОРМАЦІЙ У ТОЧЦІ МАСИВУ ҐРУНТУ

Тиск від навантаження, прикладеного до ґрунтового масиву, наприклад,

через підошву фундаменту чи бічну поверхню та вістря палі, передається в

Рис. 6.2. Аварія Трансконського елеватора в Канаді при однобічному кра-

йовому осіданні 8,4 м в умовах повної втрати стійкості його

основи

(III фаза – випинання)

, м

0,45

0,2

Рис. 6.3. Залежність осідання від розмірів

штампу при однаковому тискові

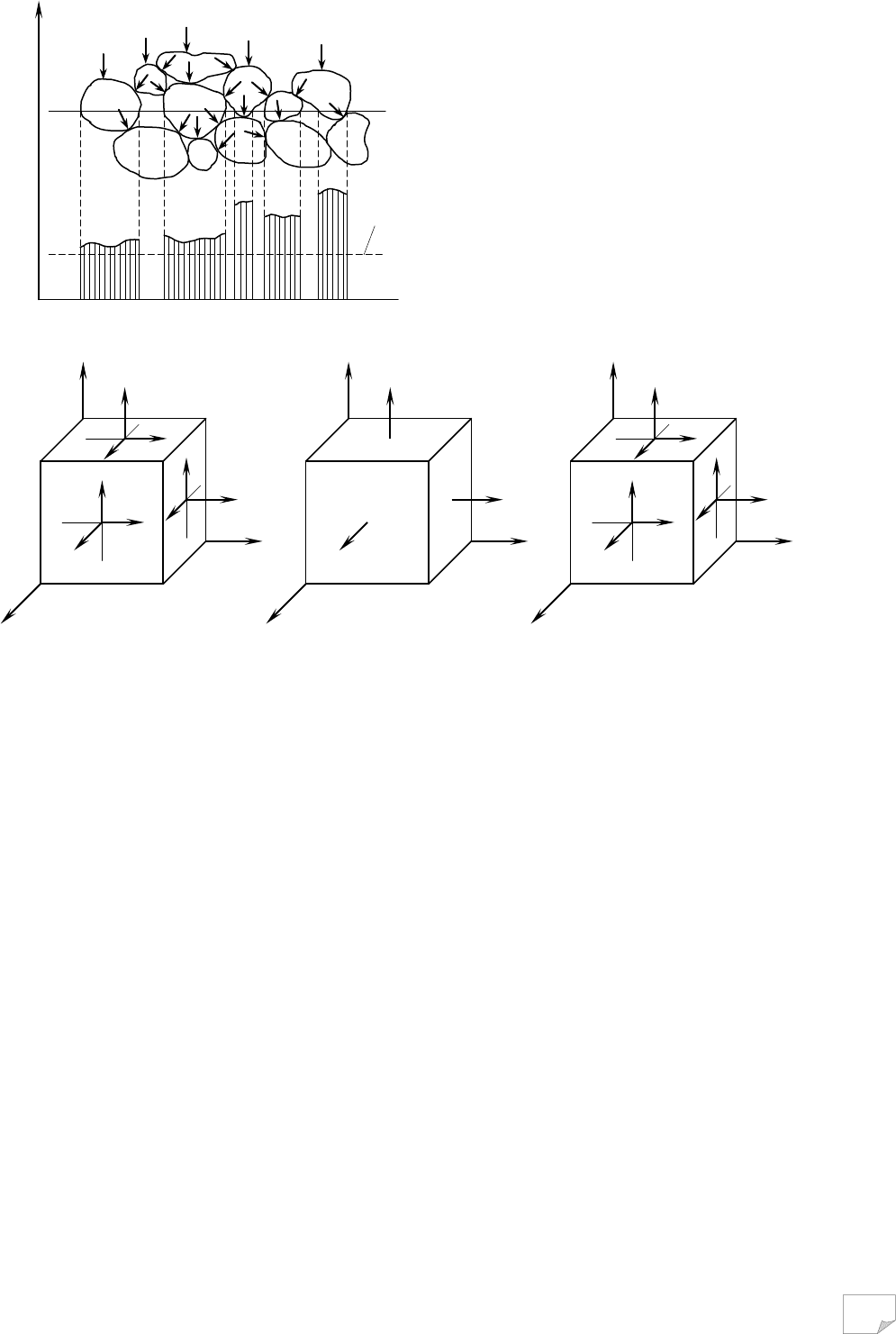
154

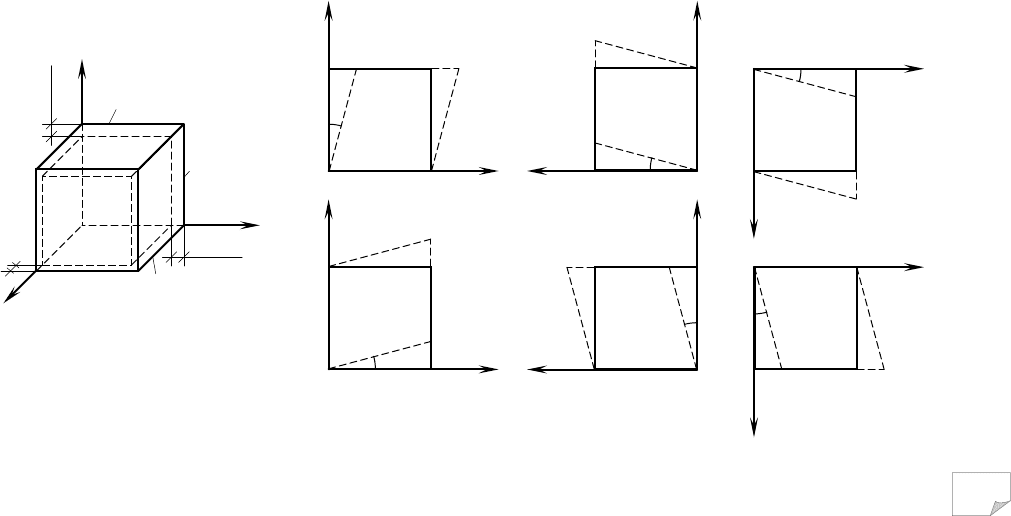
ґрунті частинками або структурними агрегатами через точки контакту, розподі-

ляючись за глибиною на все більшу площу. Напруги при цьому зменшуються.

Відбувається процес розсіювання або затухання напруг за глибиною й з відда-

ленням в сторони. Напруги σ в окремих частинках і міжчастинкових зв’язках у

межах якого-небудь виділеного перерізу, зокрема АВ на рис. 6.4, а, можуть бути

більшими, ніж їх міцність, і спричиняти руйнування. При розгляді напруженого

стану масиву ґрунту подібну місцеву концентрацію напруги, на яку може сут-

тєво впливати просторове розташування окремих часток і зв’язків між ними,

умовно не враховують (окрім моделей дискретного середовища, що описані в п.

6.4). Вважають, що вона не впливає на стійкість масиву в цілому.

Для обґрунтування цього введено поняття елементарного об’єму ґрунту,

тобто такого його об’єму, лінійний розмір якого в багато разів перевищує лі-

нійний розмір частинок або агрегатів, котрі складають цей ґрунт. Тоді, на від-

міну від суцільного середовища, для оцінювання напруг у ґрунтах, що є дис-

персними системами, реальні сили, які діють на окремі ґрунтові частинки, замі-

нюють уявними силами, розподіленими по всьому елементарному об’єму, в то-

му числі й у проміжках між частинками. Значення цих сил, віднесених до оди-

ниці площі перерізу цього об’єму умовно приймають за значення напруг у ґру-

нті (див., наприклад, лінію 2 на рис. 6.4, а).

Крім того, розміри зразка ґрунту для експериментальних визначень ха-

рактеристик його механічних властивостей у припущенні суцільності матеріалу

-σ

Рис. 6.4. Схема розподілу напруг:

а – між частинками ґрунту; б – в елемен-

тарному об’ємі ґрунту; в – у вигляді ша-

рового тензора та г – девіатора напруг;

1 – фактичні напруги у частинках ґрун-

ту; 2 – середня величина напруг у ґрунті

155

повинні бути значно більше від лінійного розміру елементарного об’єму ґрун-

ту. Використання апарату механіки суцільного середовища для розрахунків на-

пруг і деформацій у масиві ґрунту виявляється справедливим лише у випадках,

коли розміри масиву та розміри ділянок, через які передаються навантаження

на масив, значно більше від розміру елементарного об’єму ґрунту.

За підрахунками професора З. Г. Тер-Мартиросяна, у більшості випадків

для піщаних і глинистих ґрунтів ці умови завжди виконуються. 1 см

піску се-

редньої крупності містить близько 50 тис. окремих частинок. Отже, ділянки,

яких стосуються напруги й деформації, будуть мати розміри менше ніж 1 см, а

зразок для випробування ґрунту, щоб неоднорідність окремих частинок не

впливала на його властивості, може мати розміри в декілька сантиметрів. З ін-

шого боку, при ширині фундаменту, наприклад 1 м, точність визначення напруг

і деформацій в основі, складеній такими пісками, достатня для інженерних роз-

рахунків.

Мірою кількісної оцінки напружено-деформованого стану (НДС) масиву

ґрунтів є напруги, деформації та переміщення, що виникають у ньому від дії зо-

внішніх (навантаження від споруд) і внутрішніх (власна вага ґрунтів) сил. Ці

поняття відповідають загальним визначенням механіки суцільного середовища.

У системі прямокутних координат напружений стан елементарного

об’єму ґрунту можна схарактеризувати сукупністю діючих у ньому напруг (рис.

6.4, б): σ

– вертикальна нормальна напруга, що діє у напрямі осі z; σ

– горизон-

тальна нормальна напруга, що діє у напрямі осі y; σ

– горизонтальна нормальна

напруга, що діє у напрямі осі x; τ

, τ

– дотичні напруги, що діють по гранях,

паралельних осі z, однакові між собою відповідно до правила “парності напруг”

(τ

=τ

); τ

, τ

– однакові між собою дотичні напруги, що діють по гранях, па-

ралельних осі y (τ

=τ

); τ

, τ

– однакові між собою дотичні напруги, що діють

по гранях, паралельних осі x (τ

=τ

). Оскільки ґрунти, як правило, дуже погано

працюють на розтягання, в механіці ґрунтів на відміну від механіки суцільного

середовища стискаючі напруги приймають зі знаком “плюс”, а розтягаючі – зі

знаком “мінус”.

Рис. 6.5. Компоненти деформацій:

а – лінійні деформації; б – кутові деформації

б)

а)

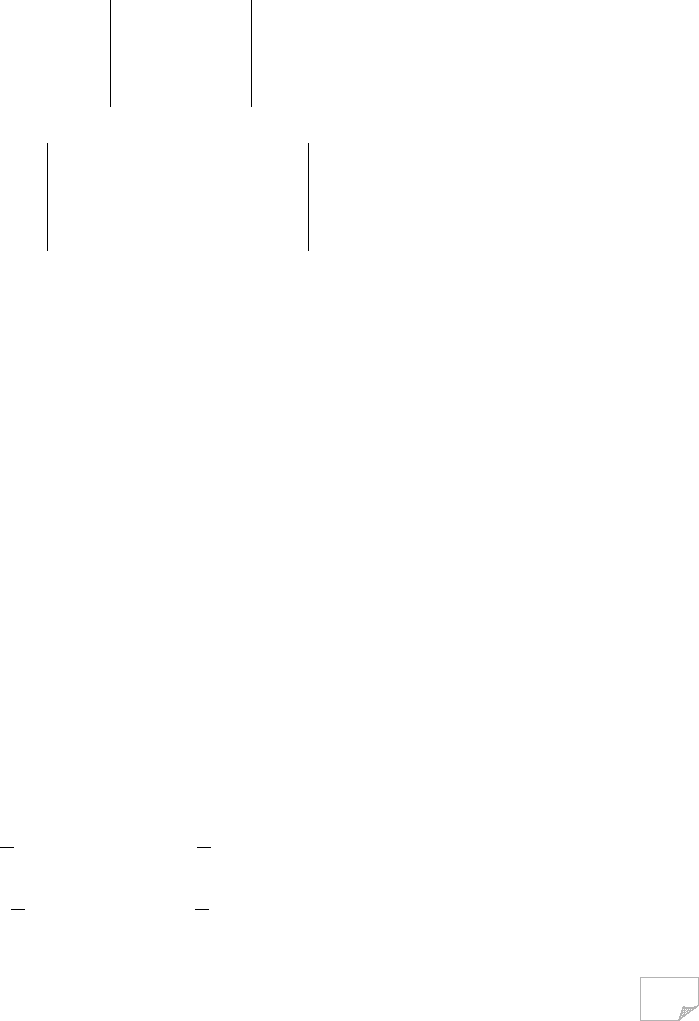
156

Деформований стан елементарного об’єму ґрунту визначають компонен-

ти: три лінійні деформації (характеризують відносні подовження ребер елемен-

тарного паралелепіпеда) ε

, ε

(рис. 6.5, а), три пари взаємно рівних кутових

деформацій (відносних зрушень – характеризують зміни кутів між гранями па-

ралелепіпеда) γ

=γ

, γ

=γ

, γ

=γ

(рис. 6.5, б) та переміщення – u, v, w. У меха-

ніці ґрунтів звичайно позитивними лінійними деформаціями вважають укоро-

чення (для кутових деформацій – зменшення кута між позитивним напрямом

осей), а негативними – подовження (для кутових деформацій – збільшення кута

між позитивним напрямом осей).

Математичний апарат для описування НДС твердого тіла докладно в технічних ВНЗ

вивчають у курсі теоретичної механіки (для тих, хто цікавиться ми рекомендуємо, напри-

клад, книги: Седов Л. И. Механика сплошной среды. – М.: Физматгиз, 1970; Ильюшин А. А.

Пластичность. – М.: Изд-во АН СССР, 1963; Вялов С. С. Реологические основы механики

грунтов. – М.: Высш. школа, 1978). Нижче розглянуті лише деякі положення цього апарату.

Дев’ять величин, що характеризують напружений стан елементарного об’єму ґрунту,

утворюють так званий тензор напруг (6.1) і називаються його компонентами:

zzyzx

yzyyx

xzxyx

σττ

τστ

ττσ

. (6.1)

За аналогією тензор деформацій характеризується матрицею

zzyzx

yzyyx

xzxyx

εγγ

γεγ

γγε

2121

. (6.2)

Величини (6.1) та (6.2) співвіднесені із системою координат x, y, z і при зміні її теж

змінюються. Однак напружений стан у точці масиву як фізичний об’єкт, звичайно, не може

залежати від довільної системи координат, і тому повинен мати характеристики, не залежні

від неї, тобто інваріантні по відношенню до системи координат. До інваріантних характери-

стик напруженого стану належать, зокрема, головні площадки й головні напруги, які можна

вказати для будь-якого тензора напруг. Три головні взаємно перпендикулярні площадки ха-

рактерні тим, що за ними діють лише нормальні напруги, а дотичні відсутні. При цьому зав-

жди приймають, що σ

≥σ

. Знаючи головні нормальні напруги, можна визначити й головні

дотичні напруги, що діють за площадками, на яких вони досягають найбільших значень:

321

/)( σστ

−=

;

132

/)( σστ

−=

;

211

/)( σστ

−=

. (6.3)

Загальний напружений чи деформований стан у точці масиву ґрунту можливо розді-

лити на дві складові. Зокрема, загальний напружений стан (або тензор напруг) (рис. 6.4, б)

виражають через суму гідростатичного напруженого стану (чи шаровий тензор), що викли-

кає зміну лише об’єму ґрунту (рис. 6.4, в), та девіаторного напруженого стану (девіатор на-

пруг), що змінює лише його форму (рис. 6.4, г). Аналогічно можна розподілити й загальний

деформований стан у точці масиву ґрунту. Це дозволяє використовувати для прогнозу пове-

дінки ґрунту інваріантні характеристики його НДС:

- середню нормальну (гідростатичну) напругу σ

, яка викликає лише зміну об’єму вирізаного

з масиву паралелепіпеда; відповідну йому середню лінійну деформацію ε

і загальну об’ємну

деформацію ε

, котрі дорівнюють

)

()(

zyxm

321

σσσσσσσ

++=++=

; (6.4)

)()(

zyxm

321

εεεεεεε

++=++=

; (6.5)

157

εε

; (6.6)

- інтенсивність дотичних напруг τ

– комбінацію напруг, наслідком дії яких є лише зміна

форми елементарного паралелепіпеда, що характеризується інтенсивністю деформацій зру-

шень γ

, де

=+++−+−+−=

)()()()(

zxyzxyxzzyyxi

222222

τττσσσσσσ

)()()( σσσσσσ

−+−+−=

; (6.7)

=+++−+−+−=

)()()()(

zxyzxyxzzyyxi

222222

γγγεεεεεεγ

)()()( εεεεεε

−+−+−= . (6.8)

Наведені інваріанти напруг і деформацій використовують при представленні резуль-

татів експериментів, для складання ряду розрахункових моделей ґрунтів.

Якщо навантаження

розподілене за смугою

(теоретично нескінченної

довжини), то така задача

має назву двовимірної або

плоскої (рис. 6.6, а). У

цьому випадку складові

напруг змінюються лише в

напрямках двох координа-

тних осей, зберігаючи пос-

тійне значення в напрямі

однієї. У випадку дії навантаження, розподіленого за площадкою обмежених

розмірів в усіх напрямах, напружений стан масиву характеризується зміною

складових напруг у напрямах трьох координатних осей. На відміну від плоскої

тривимірну задачу в механіці суцільного середовища називають просторо-

вою(рис. 6.6, б).

У класичній механіці ґрунтів для визначення напруг і деформацій засто-

совують теорію лінійно деформованого середовища. Для використання її ви-

сновків до будь-якого тіла необхідне додержання лінійної залежності між на-

пругами та деформаціями, або підпорядкування матеріалу тіла математичній

залежності, аналогічній закону Гука. При цьому наявність властивості пружних

тіл повністю відновлювати свою форму після розвантаження не обов’язкова,

якщо тільки мова йде про одноразове навантаження. У теорії лінійно дефор-

мованого середовища використовують математичні залежності теорії пружнос-

ті, але, на відміну від останньої, в ній розглядають непружні, лінійно деформо-

вані тіла при їх одноразовому навантаженні. Для використання у класичній ме-

ханіці ґрунтів апробованих розв’язань приймають деякі припущення й обме-

ження, як-от: розрахунки ведуть лише в інтервалі навантажень, у межах котрих

ґрунт можна вважати лінійно деформованим, а також вважають ґрунт за су-

цільне, однорідне та ізотропне середовище. Не відображає теорія пружності й

деформації ґрунтів у часі.

Рис. 6.6. Схеми навантажень для:

а – плоскої задачі; б – просторової задачі

ℓ

-∞

+∞

158

6.4. МОДЕЛІ, ЩО ОПИСУЮТЬ СТАН ҐРУНТУ

Для розв’язання задач механіки ґрунтів звичайно обмежуються вивченням лише ме-

ханічних явищ і відволікаються від фізико-хімічних та інших процесів, які відбуваються в

ґрунтах. Таким чином, механіка ґрунтів має справу не з реальними гірськими породами, як із

природно-історичними тілами, а з їх певними механічними моделями – тілами зі значно

спрощеними властивостями порівняно з фактичними ґрунтами.

Спроби описати весь комплекс різних властивостей ґрунтів за допомогою однієї мо-

делі потребують розроблення складного математичного апарату розрахунків, проведення

трудомістких експериментів для визначення параметрів моделі і все-таки навряд чи можуть

дати позитивний результат найближчими роками. Та навіть, якщо ці спроби й будуть успіш-

ними, то досить очевидно, що така модель виявиться практично непридатною для вирішення

прикладних задач через її складність.

Відсутність єдиної “найкращої” моделі ґрунту призвела до створення великої кількос-

ті моделей, що так чи інакше застосовують у механіці ґрунтів. Як зазначає

В. Г. Федоровський (1985), поділ моделей ґрунтів на класи навряд чи може бути однознач-

ним, бо в одній моделі можна зустріти не лише характеристики різних напрямів, але і класи-

фікаційних ознак дуже багато, причому ці ознаки досить тісно взаємопов’язані й не є неза-

лежними.

Розглянемо спершу лише моделі ґрунтів, що зводяться до співвідношення типу “на-

пруга – деформація” для елементарних об’ємів, а не моделі основ у цілому або контактні мо-

делі. Найбільш загальний поділ усіх моделей можна виконати за ознакою, входить чи ні в їх

рівняння час (у явній чи неявній формі). Моделі, що враховують часові ефекти, звичайно на-

зивають реологічними (або t-моделями). Їх отримують переважно зі статичних моделей (які

час не беруть до уваги) додаванням в’язкості (як це нижче розглянуто в моделях Максвелла

чи Бінгама) в тій чи іншій формі. Є й більш складні

-моделі, котрі не виводяться прямо із

статичних. До цих моделей примикає й розгляд взаємодії скелета ґрунту з поровою рідиною.

Детально реологічні моделі ґрунтів розглянуті в посібнику: Вялов С. С. Реологичес-

кие основы механики грунтов. – М.: Высш. школа, 1978; монографіях: Ширинкулов Т. Ш.,

Зарецкий Ю. К. Ползучесть и консолидация грунтов. – Ташкент: Фан, 1986; Тер-

Мартиросян З. Г. Реологические параметры грунтов и расчеты оснований сооружений. – М.:

Стройиздат, 1990.

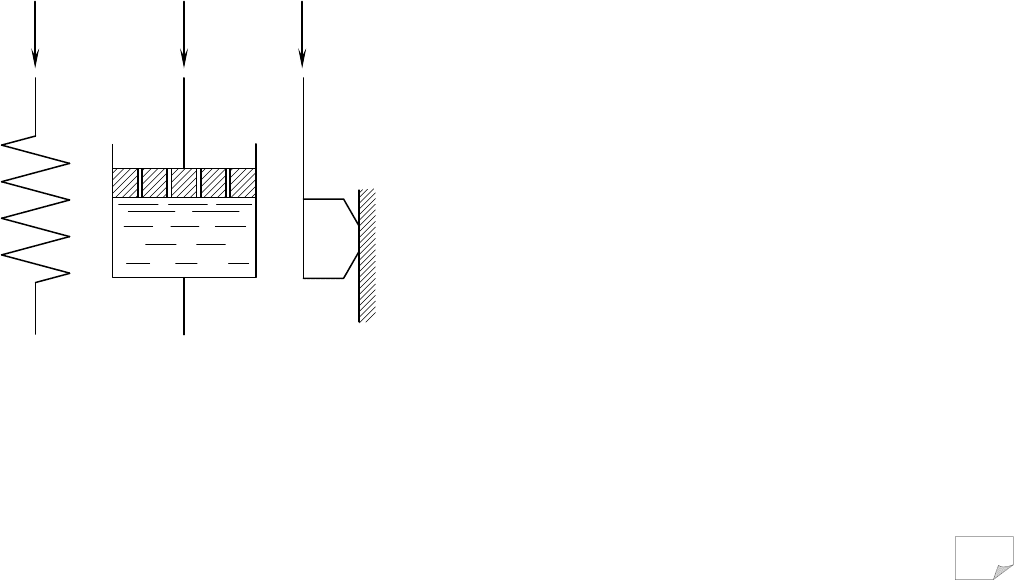
У реології пружні, в’язкі та пластичні власти-

вості тіл досить наочно моделюють набором механі-

чних елементів (звідси термін “механічні моделі”),

які з’єднують паралельно чи послідовно. Так, іде-

альне пружне тіло (або елемент) Гука (рис. 6.7, а)

моделюють пружиною й позначають символом H.

Вважають, що при навантаженні елемент одержує

миттєві лінійні та оборотні деформації. Залежності

між напругами σ (τ) і деформаціями ε (γ) мають ви-

гляд

εσ E

або

γτ

∞

, (6.9)

де E і G

∞

– модуль пружності та гранично-тривале

значення модуля зрушення.

В’язкі властивості тіл моделюють як циліндр,

наповнений рідиною, в яку занурюють дірчастий по-

ршень (рис. 6.7, б). Цей елемент (в’язке тіло Нью-

тона) ще називають демпфіруючим елементом та

позначають N. За законом Ньютона швидкість (



чи



) занурення поршня прямо пропорційна напрузі й

зворотно – в’язкості при об’ємному стисненні η

чи

Рис. 6.7. Механічні моделі: а – пруж-

не тіло Гука; б – в’язке тіло

Ньютона;

в – пластичне тіло Сен-Венана

159

в’язкості η рідини:

/ησε



або

εησ



, чи

γητ



або

ητγ /



. (6.10)

Пластичні властивості відображають ідеальним пластичним тілом (елементом сухого

тертя) Сен-Венана, яке позначають символом SV (рис. 6.7, в), що враховує властивість ма-

теріалу деформуватися тільки після перевищення напругою деякої межі (σ

чи τ

Послідовне з’єднання елементів позначають за допомогою тире (наприклад, H-N), а

паралельне – вертикальної риски (наприклад, H/N). Три наведені елементи можна з’єднувати

в різноманітних комбінаціях, які й будуть відображати різні пружно-в’язкі властивості тіл.

При цьому певні параметри рівнянь стану підлягають експериментальному (феноменологіч-

ному) визначенню. Але численні досліди показали суттєву різницю між рівняннями дефор-

мування ґрунтових моделей та дійсною поведінкою ґрунтів. А от при розгляді якісного боку

процесу деформування ґрунтів такі реологічні моделі дуже наочні. Нижче ми в історичному

розвитку розглянемо найбільш популярні з них.

Зазначимо також, що в більшо-

сті випадків механічні моделі опису-

ють реологічні властивості ґрунту при

зрушенні. Це пов’язано з історичним

розвитком реології ґрунтів, коли спе-

ршу виникла необхідність прогнозу

деформацій зсування. Деякі з цих мо-

делей застосовують і при описі дефо-

рмацій ущільнення. Тоді у рівняннях

міняють τ на σ, G на E, η на η

, γ на ε.

Далі будемо записувати реологічні

моделі ґрунту лише при його зсуван-

ні.

Тіло Кельвіна-Фойгта (позна-

чають символом K) утворено парале-

льним з’єднанням пружного та в’язкого елементів (рис. 6.8, а): K=H/N. Реологічне рівняння

стану цього тіла можна вивести, склавши рівняння моделі

τττ

, (6.11)

де τ

і τ

– напруги в пружному й в’язкому елементах.

З урахуванням (6.9) та (6.10) це рівняння має вигляд

G γηγτ

∞

. (6.12)

При напрузі τ=const з (6.12) отримуємо закономірність зміни деформації з часом

( )

/tG

∞

−

∞

−= 1

. (6.13)

Це рівняння описує зростання деформації, графік якої подано на рис. 6.7, а від нуля до

кінцевого стабілізованого значення

∞∞

G/τγ

. Величину

TG/

∞

називають часом піс-

лядії чи запізнювання деформації. При постійній деформації γ=const напруга, як видно з

(6.12), залишається постійною

γτ

∞

(рис. 6.8, а). Отже, тіло Кельвіна-Фойгта має власти-

вість післядії, але не проявляє властивість релаксації.

Тіло Максвелла (позначають символом M) утворено послідовним з’єднанням пружно-

го та в’язкого елементів (рис. 6.8, б): M=H-N. Реологічне рівняння стану цього тіла можна

одержати, склавши рівняння моделі

γγγ

, (6.14)

де γ

і γ

– відповідно деформації пружного й в’язкого елементів.

Прийнявши γ

=τ/G

– умовно-миттєвий модуль зрушення) і γ

=τ/η, після дифере-

нціації (6.14) отримуємо

Рис. 6.8. Моделі пружно-в’язких тіл:

а – Кельвіна-Фойгта; б –

Максвелла;

в – узагальненого пружно-в’язкого тіла