Асанов А.З. Введение в математическое моделирование динамических систем
Подождите немного. Документ загружается.

2.5. Методика формирования математических моделей
динамических систем
При исследовании динамических объектов и систем, как правило,
интересуются так называемой динамикой систем – способностью систем
изменять свое состояние под воздействием внешних воздействий. В этом
случае математическая модель динамической системы и ее элементов
представляется в виде уравнений динамики, которые могут записываться в
форме дифференциальных, интегральных и др. уравнений. Уравнения
движения описывают динамику
системы, переход ее из одного равновесного
(статического, установившегося) состояния в другое под действием входных
координат (переменных).
Поведение системы на равновесных режимах описывается уравнениями
статики, которые представляют собой алгебраические (линейные или
нелинейные) уравнения. К равновесным (установившимся) режимам
относятся состояние покоя, равномерные и равноускоренные движения
системы. Уравнения установившихся режимов, при которых управляющие
и
возмущающие воздействия принимаются постоянными, обычно являются
алгебраическими уравнениями. Эти уравнения достаточно просто можно
получить, если известны уравнения динамики: уравнения статики
(алгебраические уравнения) можно получить из дифференциального
уравнения динамики при его вырождении, когда приравниваются к нулю все
производные или операторы дифференцирования.
Наиболее распространенным подходом к составлению уравнений
движения динамической системы
является подход, когда система условно
разбивается на множество физически однородных элементов (звеньев). Далее
для каждого элемента составляют дифференциальные (алгебраические,
интегральные и др.) уравнения, описывающие исследуемые процессы, явле-
ния характеристики, на основе того физического закона, которому подчиня-
ется процесс, протекающий в данном элементе. На последующем этапе с
помощью, как правило, алгебраических
уравнений описывают связи между
входными и выходными сигналами (переменными) элементов системы.
Таким образом, уравнения движения системы в целом есть множество
уравнений движения элементов, образующих эту систему, в совокупности с
уравнениями, описывающими взаимосвязи элементов друг с другом.
Одной из наиболее сложных проблем моделирования является проблема
47
адекватности полученного математического описания реальным
физическому процессу или системе. Если процесс достаточно прост или
хорошо известны физические законы и их взаимодействия в системе, то
уравнения, описывающие процесс, получается непосредственно из
физических законов, действующих в этом процессе. Но в общем случае
присутствует неопределенность в наших представлениях о явлениях в
системе,
и хорошее математическое описание можно получить только в
результате большого количества экспериментов. В результате таких
экспериментов и априорных теоретических знаний получаются соотношения,
связывающие доступные для наблюдения выходные сигналы и допустимые
входные сигналы системы.
Поэтому существуют два принципиально различных подхода к построе-
нию математических моделей систем и их элементов: эмпирический
(экспериментальный) и теоретический (аналитический).
При эмпирическом подходе по реакции элемента (
системы) на
различные сигналы и внешние условия возможно построение
математической модели. Достаточно знать поведение выходных переменных
элемента на известные входные переменные. После выбора вида уравнений
движения или функциональной зависимости между этими переменными
решается задача определения параметров модели и оценки адекватности ее
реальным процессам.
При теоретическом подходе математическая модель строится на
основании
физического закона, описывающего движение элемента системы.
В качестве физического закона могут быть рассмотрены уравнения
сохранения энергии, баланса массы, расходов, потоков и количества
движения и т.д.
Получающиеся уравнения движения, как правило, являются
нелинейными. В общем виде отыскать аналитическое решение нелинейного
неоднородного дифференциального уравнения не всегда возможно. В этом
случае практически
единственным способом решения таких уравнений
является использование средств вычислительной техники в совокупности с
методами и алгоритмами вычислительной математики (численное решение
уравнений). Часто задачу интегрирования нелинейных уравнений удается
свести к более простой задаче – задаче решения линейных
дифференциальных уравнений. Эта процедура сведения нелинейных
48
уравнений к линейным называется линеаризацией дифференциальных
уравнений. При этом достаточным условием линеаризации является
отсутствие в исходной нелинейной зависимости разрывов первого и второго
рода, наличие производных всех порядков и справедливость уравнения в
течение всего интервала переходного процесса. Сам метод линеаризации
называется методом малых отклонений.
В большинстве случаев уравнения элементов и
самих динамических
систем оказываются нелинейными. Однако в одних случаях нелинейности
являются несущественными, не вносящими качественно нового в процесс
функционирования, в других они носят определяющий характер и вносят
принципиально новые существенные особенности в процесс функциони-
рования системы. Поэтому при составлении дифференциальных уравнений
необходим анализ возможности и допустимости их упрощения и, в
частности
, линеаризации.
Алгоритм составления уравнений динамики следующий:
• формулируется задача, для решения которой создается математическая
модель системы, определяются входные, выходные и прочие переменные
величины, условия, ограничения и т.д.;
• динамическая система разбивается на элементы (звенья), (как правило,
элементы должны быть физически однородны);
• для каждого элемента (звена) составляется соответствующее уравнение на
основании того фундаментального (если таковое есть) физического
закона, который определяет процесс, протекающий в данном элементе;
• при необходимости осуществляется линеаризация полученных
соотношений;
• с помощью уравнений (как правило, алгебраических) описываются связи
элементов (звеньев) динамической системы друг с другом;
• при необходимости выполняются преобразования для изменения
количественных мер отсчета и изменения размерности;
• совокупность уравнений динамики всех звеньев и уравнений связи
образует математическую модель динамической системы.
Приведенный выше способ описания динамических систем принято
называть поэлементным описанием или поэлементной (компонентной)
моделью. Для такого описания динамической системы характерно большое
49
количество дифференциальных и алгебраических уравнений различного
порядка с большим количеством промежуточных переменных.
Формирование математической модели процесса, объекта, системы – это
первый и весьма важный этап при любых исследованиях и решении
различных задач, но далеко не последний.
Следующим этапом является анализ математической модели. На этом
этапе исследуются общие свойства модели – доказательства
существования
решения задачи, для которой строится модель, доказательства
единственности/неединственности решения, в каких пределах изменяются
переменные, каковы тенденции их изменения и т.д. В случае отсутствия
решения требуемой задачи возникает необходимость корректировки
постановки задачи, способов ее математической формализации. Но в
реальной практике модели сложных объектов и процессов с большим трудом
поддаются
аналитическому исследованию, а упрощения модели приводят к
недопустимым результатам, связанным с потерей адекватности. В этих
ситуациях необходим переход к численным методам исследований.
Этап численного решения (цифровое моделирование) задачи включает в
себя разработку алгоритмов численного решения задачи, составления
программ для ЭВМ и непосредственное проведение расчетов. Здесь
актуальны различные методы обработки данных
, решения разнообразных
уравнений. Нередко расчеты по математической модели носят
многовариантный имитационный характер. Благодаря высокому
быстродействию современных ЭВМ удается проводить многочисленные
эксперименты, изучая поведение модели при различных сочетаниях и
изменениях некоторых условий.
Этап анализа численных результатов заключается в оценке
корректности полученных результатов численного моделирования, в оценке
адекватности модели изучаемым явлениям, процессам,
сложным объектам.
Эти этапы собственно использования полученной математической модели
будут рассмотрены отдельно в разделах, посвященных задачам анализа и
синтеза. Для проведения этих работ, как правило, осуществляют переход от
поэлементного описания к другим формам математического описания
динамической системы: ко вход-выходному дифференциальному уравнению,
передаточным функциям, моделям в пространстве состояний и пр., о
которых
речь пойдет в следующих разделах.
50

2.6. Базовые этапы математического моделирования
различных систем
2.6.1. Формирование уравнений модели электрических систем.
Законы Кирхгофа, Максвелла
Электрические системы представляют собой совокупность устройств,
предназначенных для прохождения электрического тока. Эта совокупность
устройств образует электрическую цепь. Электромагнитные процессы в этих
устройствах могут быть описаны с помощью понятий напряжения и тока.
Источниками электрической энергии являются гальванические
элементы, аккумуляторы, генераторы и другие устройства, в которых
происходит процесс преобразования химической, молекулярно-кинетической,
тепловой
, механической или другого вида энергии в электрическую.
Приемниками электрической энергии, или так называемой нагрузкой,
служат электрические лампы, электронагревательные приборы,
электрические двигатели и другие устройства, в которых электрическая
энергия превращается в световую, тепловую, механическую и т. п.
Расчеты электрических систем (цепей) и исследования процессов,
происходящих в них, основываются на различных допущениях и некоторой
идеализации реальных объектов электрических цепей.
Под элементами в теории электрических цепей подразумеваются
обычно не физически существующие составные части электротехнических и
радиотехнических устройств, а их идеализированные модели, которым теоре-
тически приписываются определенные электрические и магнитные свойства
так, что они в совокупности приближенно отображают явления,
происходящие в реальных устройствах.
В теории
электрических цепей различают активные и пассивные
элементы. Активными элементами считаются источники электрической
энергии: источники напряжения и источники тока. К пассивным элементам
электрических цепей относятся сопротивления, индуктивности и емкости.
Соответственно различают активные и пассивные цепи; активные цепи
содержат источники электрической энергии, пассивные же цепи состоят
только из пассивных элементов.
Ток. Численно
электрический ток определяется как
dq
i
dt
=
, где через q
51
обозначено количество электричества. В Международной системе единиц СИ
i измеряется в амперах, q — в кулонах или ампер-секундах.
Электрический ток может быть постоянным или переменным, т. е.
изменяющимся в зависимости от времени.
Направление тока характеризуется знаком тока. Положительное
направление тока выбирается произвольно; оно обычно указывается
стрелкой. Если в результате расчета тока, выполненного с учетом выбранного
положительного направления, ток имеет знак плюс (
), то это означает,
что его направление совпадает с выбранным положительным направлением.
В противном случае, когда ток отрицателен (
0i >
0i
<
), он направлен
противоположно.
Напряжение. Разность электрических потенциалов двух различных
точек цепи представляет напряжение
на данном участке цепи; оно может
быть постоянным или переменным. В системе СИ напряжение и измеряется в
вольтах. Разность электрических потенциалов – скалярная величина.
u
Положительное направление напряжения чаще всего выбирают
совпадающим с положительным направлением тока.
Положительными направлениями (или просто направлением) токов и
напряжений пользуются при исследовании процессов, происходящих в
электротехнических устройствах,
и при расчете электрических цепей.
Энергия. Мгновенная мощность, поступающая в приемник, равна
произведению мгновенных значений напряжения и тока:
Pui
=
.
Мгновенная мощность
P
– величина алгебраическая; она положительна
при одинаковых знаках
u
и и отрицательна при разных знаках
u
и
i
.
i
Если положительные направления для напряжения и тока приняты
совпадающими, то при
энергия поступает в приемник, а при
энергия возвращается из рассматриваемого участка цепи обратно к
источнику.
0P > 0P <
Энергия, поступившая в приемник за промежуток времени от
до ,
выражается интегралом
.
1
t
2
t
2
1
t
t
WPd=
∫
t
В отличие от мгновенной мощности
P
, которая может иметь отри-
цательный или положительный знак, энергия, поступившая в приемник,
всегда имеет положительный знак.
52

В системе СИ работа и энергия измеряются в джоулях, мощность – в
ваттах.
Сопротивление. Сопротивлением называется идеализированный элемент
цепи, характеризующий потери энергии на нагрев, механическую работу или
излучение электромагнитной энергии.
Следует заметить, что термин «сопротивление» и соответствующее ему
условное обозначение
применяются в электротехнике и радиотехнике для
обозначения как самого элемента, в котором происходит необратимый
процесс поглощения электромагнитной энергии, так и для количественной
оценки величины, равной отношению напряжения на данном элементе
цепи к току, проходящему через него:
R
u
R
i
=
(закон Ома).
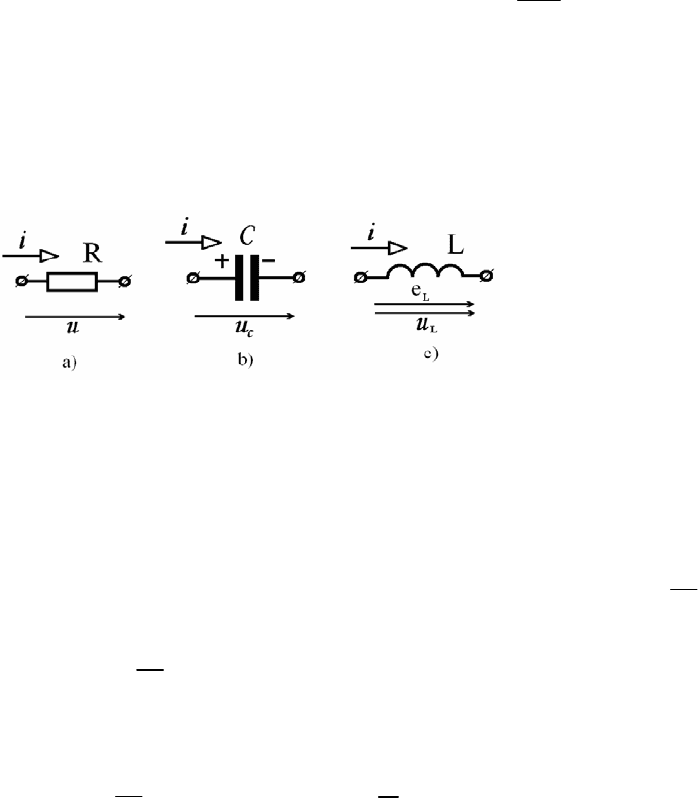
Ус л о в н о е графическое изображение сопротивления показано на рис. 2.6.1-а
Здесь предполагается, что положительные направления тока и на-
пряжения совпадают; при этом знаки
и одинаковы и
u i
0
R
> . В системе СИ
сопротивление
измеряется в омах. R
Мгновенная мощность, поступающая в сопротивление, равна про-
изведению мгновенных значений напряжения и тока:
2
R
PuiRi==
.
Электрическая энергия, поступившая в сопротивление и превращенная в
тепло (впервые было доказано Джоулем и Ленцем), выражается формулой:
2
00
tt
RR
WPdtRi==dt
∫
∫
.
В случае постоянного тока (
i const
=
), .
2
R
WRi= t
Индуктивность. Индуктивностью
L
называется идеализированный
элемент электрической цепи, приближающийся по свойствам к индуктивной
катушке, в которой накапливается энергия магнитного поля.
При этом термин «индуктивность» и соответствующее ему условное
обозначение
L
применяются для обозначения как самого элемента цепи,
способного накапливать энергию магнитного поля, так и для количественной
оценки отношения потокосцепления самоиндукции к току в данном элементе
L
i
Ψ
=
.
Потокосцеплением самоиндукции
Ψ
цепи называется сумма
53
произведений магнитных потоков, обусловленных только током в этой цепи,
на числа витков, с которыми они сцеплены. Если все витки пронизываются
одним и тем же магнитным потоком, то потокосцепление равно
произведению магнитного потока на число витков.
В системе СИ
измеряется в веберах, Ψ
L
– в генри. При этом всегда
потокосцепление и ток имеют одинаковый знак, так что
0
L
> .
Зависимость потокосцепления от тока в общем случае нелинейная, и
параметр
L
зависит от тока. В случае, когда характеристика
Ψ
прямолинейна, индуктивность
L
постоянна (линейная индуктивность).
На основании закона электромагнитной индукции Фарадея – Максвелла
изменение потокосцепления самоиндукции вызывает электродвижущую силу
(Э.Д.С.) самоиндукции, которая выражается формулой
L
d
e
dt
Ψ
=−
.
По закону Ленца, выражающему принцип электромагнитной инерции,
эта Э.Д.С. противодействует изменению потокосцепления, что и учитывается
знаком минус, поскольку положительное направление для
L
e
выбрано
совпадающим с положительным направлением
.
i
Рис. 2.6.1. Условные обозначения элементов электрической системы
Ус л о в н о е графическое изображение индуктивности с указанием вы-
бранных положительных направлений тока и Э.Д.С. самоиндукции
приведено на рис. 2.6.1-с.
Если
не зависит от
i
, то предыдущая формула принимает вид: L
L
di
eL
dt
=−
.
Величина
LL
di
ueL
dt
=− =
называется падением напряжения в
индуктивности, или, что то же, напряжением на индуктивности.
Таким образом,
L
di
uL
dt
=
, тогда
0
1
() (0)
t
L
it i udt
L
=+
∫
. (2.6.111)
Мгновенная мощность, поступающая в индуктивность, равна произ-
ведению мгновенных значений напряжения и тока:
54

LL
di
PuiLi
dt
==
.
Она связана с процессом нарастания или убывания энергии магнитного поля.
Энергия магнитного поля за произвольный отрезок времени
определяется по формуле
[0, ]t
22
0
22
t
L
Li
WLidi
L
Ψ
===
∫
.
Если часть магнитного потока, связанного с индуктивным элементом,
связана одновременно и с другим индуктивным элементом, то эти два
элемента, кроме параметров
1
L
и
2
L
, обладают параметром
M
, называемым
взаимной индуктивностью. Взаимная индуктивность представляет собой
отношение потокосцепления взаимной индукции одного из элементов к току
в другом элементе:
12 21
21
M
ii
Ψ
Ψ
==
,
где
– потокосцепление первого элемента, обусловленное током второго
элемента;
– потокосцепление второго элемента, обусловленное током
первого элемента.
12
Ψ
21
Ψ
В этом случае в первом и во втором элементах наводятся Э.Д.С.
взаимной индукции, равные соответственно:
12 2 21 1
12
;;
MM
ddi d
eMe
dt dt dt dt
ΨΨ
=− =− =− =−
di
M
Эти выражения получены в предположении, что
M
не зависит от и ,
так как здесь рассматриваются линейные цепи.
1
i
2
i
Взаимная индуктивность
M
измеряется, так же как и индуктивность
L
,
в генри. Однако в отличие от параметра
L
взаимная индуктивность
M
обозначает не какой-либо самостоятельный элемент электрической цепи, а
лишь магнитную связь между индуктивными элементами.
Емкость. Емкостью называется идеализированный элемент
электрической цепи, приближенно заменяющий конденсатор, в котором
накапливается энергия электрического поля.
При этом термин «емкость» и соответствующее ему буквенное обозна-
чение
применяются для обозначения как самого элемента цепи, спо-C
55

собного накапливать энергию электрического поля, так и для количественной
оценки отношения заряда к напряжению на этом элементе:
C
q
C
u
=
.
Если
и измеряются в кулонах и вольтах, то измеряется в
фарадах. При этом всегда заряд и напряжение имеют одинаковый знак, так
что
.
q
C
u
C
0C >
Зависимость заряда от напряжения в общем случае нелинейна, и,
следовательно, параметр
зависит от напряжения. В случае, когда
характеристика
прямолинейна, емкость постоянна (линейная
емкость). Здесь рассматриваются только линейные емкости.
C
()qu
C
С изменением напряжения на емкости в присоединенной к ней по-
следовательно электрической цепи создается ток, величина которого
определяется скоростью изменения заряда на емкости:
C
dq du
iC
dt dt
==
.
Таким образом,
C
du
iC
dt
=
, тогда
0
1
(0)
t
CC
uu id
C
=+t
∫
. (2.6.1222)
Ус л о в н о е графическое изображение емкости на рис. 2.6.1-b.
Мгновенная мощность, поступающая в емкость, равна:
C
CC C
du
PuiCu
dt
==
.
Она связана с процессом накопления или убыли электрического заряда в
емкости. Когда заряд положителен и возрастает, то ток положителен, и в
емкость поступает электрическая энергия из внешней цепи. Когда заряд
положителен, но убывает, т. е. ток отрицателен, то энергия, ранее
накопленная в электрическом поле емкости, возвращается во внешнюю цепь.
Энергия
электрического поля в произвольный момент времени опре-
делится по формуле
t
22
0
22
C
u
C
CCC
Cu q
WCudu
C
===
∫
.
Источник Э.Д.С. Источник тока. В теории электрических цепей
пользуются идеализированными источниками электрической энергии:
источником Э.Д.С. и источником тока. Им приписываются следующие
свойства.
56
