Greenwood D.T. Advanced Dynamics
Подождите немного. Документ загружается.

399 Problems
z
(0) = 0, η(0) = 1. (a) Use Euler’s dynamical equations and the (˙, ˙η) kinematical
equations to obtain numerical values of ω
x
,ω
y
,ω
z
,
x
,
y
,
z
,η by integrating over
the time interval 0 ≤ t ≤ 1 s. For times within this interval, calculate the work W
done by M
z
and also the angular deviation α of the x-axis from its original orientation,
where α = cos
−1
(1 −2
2
y
− 2
2
z
). (b) Find W
max
and the time at which it occurs. (c)
Determine α
max
and the time of occurrence. (d) Find the time at which ω
x
,ω
y
,ω
z
simultaneously return to their original values.
6.10. A thin uniform disk of mass m and radius r rolls without slipping on a horizontal
surface. The generalized coordinates are (ψ, θ, φ, X, Y ) where (ψ, θ, φ) are type
I Euler angles, and (X, Y ) is the location of the contact point. The contact point
has a velocity r
˙
φ at an angle ψ with the positive X -axis, that is,
˙
X = r
˙
φ cos ψ
and
˙
Y =−r
˙
φ sin ψ. Choose (
˙
ψ,
˙
θ,)asus where =
˙
φ −
˙
ψ sin θ is the angu-
lar velocity of the disk about its symmetry axis. Assume that g/r = 20 s
−2
, where
g = 9.81 m/s
2
and r = 0.4905 m. (a) Derive the three differential equations of mo-
tion, that is, equations for
˙
usintermsofqs and us. (b) Assume the initial conditions
ψ(0) = 0, θ (0) = π/6, φ(0) = 0, X (0) = 0, Y (0) = 0,
˙
ψ(0) = 4 rad/s,
˙
θ(0) = 0,
(0) = 2 rad/s. Use numerical integration to obtain the values of the qs and us over
the interval 0 ≤ t ≤ 3.5s.Findθ
min
and the following θ
max
with their corresponding
times, as well as the times when θ = 0. Show that the motion of θ is periodic, but the
path of the contact point on the XY-plane is not periodic.
mg
r
i
j
(X, Y )
disk
θ
⭈
.
.
Figure P 6.10.
6.11. A dumbbell consists of two particles, each of mass m, connected by a massless rod of
length l (Fig. P 6.11). Given that m = 1 kg, l = 1 m, and g = 9.8m/s
2
. Choose (x,θ)
as generalized coordinates and assume the initial conditions x(0) =
1
2
m,
˙
x(0) = 0,
θ(0) = 0,
˙
θ(0) =
1
2
rad/s. As the dumbbell falls due to gravity and slides without
friction, particle A hits the wall inelastically. Then it slides down the wall until it
finally leaves and moves to the right. Use the notation v ≡
˙
x, ω ≡
˙
θ. Consider three
phases of the motion.
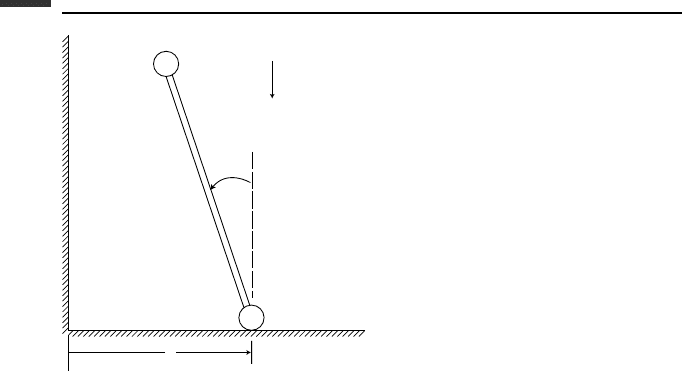
400 Introduction to numerical methods
m
x
e = 0
l
g
m
A
B
θ
Figure P 6.11.
Phase 1 – before impact (a) Derive the four first-order differential equations of motion.
(b) Integrate these equations numerically and tabulate values of x,θ,v,ω, at each 0.1s
from zero to just before the time of impact.
Phase 2 – impact (c) Find the time of impact and the corresponding values of x and θ .(d)
What are the values of
˙
x and
˙
θ just before impact. (e) Solve for
˙
x and
˙
θ immediately after
impact and also the horizontal impulse
ˆ
λ of the wall acting on particle A.
Phase 3 – after impact (f) Given the constraint equation
˙
x −l
˙
θ cos θ = 0, obtain expres-
sions for
¨
x and
¨
θ which are to be integrated numerically. (g) Find the time at which particle
A leaves the wall and give the corresponding values of x,θ,v, and ω.

Appendix
A.1 Answers to problems
Chapter 1
1.1. (a)
˙
x = m
2gr
m
0
(m + m
0
)
,
˙
θ =−
2g(m + m
0
)
m
0
r
(b) x
max
=
2mr
m + m
0
1.2. θ
max
= 120
◦
1.3. v
1
=−
1
5
v
0
i, v
2
, v
3
=
v
0
5
(3i ±
√
3j)
1.4. v =
1
3
v
0
, all particles
1.5. ρ =
v
2
0
cos
2
θ
0
g cos
3
θ
1.6. 1.79 cm higher on west bank
1.7. m
¨
l + kl − ml
˙
θ
2
− mg cos θ = kL
ml
¨
θ + 2m
˙
l
˙
θ + mg sin θ = 0
1.8. (a) v = v
0
1 −e
−
c
m
t
, (b) W = mv
2
0
1 −e
−
c
m
t
,
(c) W = mv
2
0
= 2T ,
1.9.
ˆ
F
i
= cl
1.10. (a) v
10
= 0.6302 v
0
,(b)v
9
= 0.03317v
0
1.11. (a)
˙
x =−
1
3
v
0
,
˙
θ =−
2
√
2 v
0
3l
(b)
ˆ
Q
y
=
4
3
mv
0

402 Appendix
1.12. (a)
˙
x =
v
0
√
2
,
˙
y =
v
0
3
√
2
,ω=
4v
0
3l
(b)
ˆ
F =
2
3
mv
0
1.13. (a) ω =
v
0
2
√
2l
, (b) v
A
=
1
4
v
0
i
1.14. (a) l
¨
φ +r ω
2
0
sin φ = 0, (b) φ
max
= 60
◦
1.15. ω =
2r
ˆ
F
m(r
2
+l
2
− 2rl cos θ )
,
ˆ
R
h
=
(r
2
−l
2
)
ˆ
F
r
2
+l
2
− 2rl cos θ
ˆ
R
v
=
2rl sin θ
ˆ
F
r
2
+l
2
− 2rl cos θ
1.16. (a)
˙
θ =
2
ˆ
F
(5 −
√
3µ)ml
,
˙
x =
2(1 −
√
3µ)
ˆ
F
3(5 −
√
3µ)m
,
(b) µ
min
=
1
√
3
1.17. (a) 2mr
¨
θ = mg(1 −µ) sin θ − mg(1 + µ) cos θ + 2µmr
˙
θ
2
(b) P =
1
2
mg[(1 + µ) sin θ + (1 − µ) cos θ ]
1.18. v
0
=
ch
m
1 −
π
4
1.19. (a)
¨
x =
l
˙
θ
2
cos θ
1 +cos
2
θ
,
¨
θ =
˙
θ
2
sin θ cos θ
1 +cos
2
θ
, P =
ml
˙
θ
2
1 +cos
2
θ
(b)
˙
x =
v
0
sin θ
2(1 +cos
2
θ)
,
˙
θ =
2
1 +cos
2
θ
v
0
l
1.20. (a) m
1
¨
x
1
= k(x
2
− x
1
)
1 −
L
l
+ F
m
1
¨
y
1
= k(y
2
− y
1
)
1 −
L
l
m
2
¨
x
2
= k(x
1
− x
2
)
1 −
L
l
m
2
¨
y
2
= k(y
1
− y
2
)
1 −
L
l
where l =
(x
2
− x
1
)
2
+ (y
2
− y
1
)
2
(b) m
1
¨
x
1
= k(x
2
− x
1
)
1 −
L
l
+ F

403 Answers to problems
m
1
¨
y
1
= k(x
2
− y
1
)
1 −
L
l
m
2
¨
x
2
=−
1
2
k(2x
2
− x
1
− y
1
)
1 −
L
l
1.21. (a) θ
max
= tan
−1
1.1732 = 49.56
◦
(b) θ = 34.86
◦
1.22. (a) Upward
¨
y =
˙
y
2
− gy
L − y
Downward
¨
y =
2L −3y
3L −3y
g
1.23. (a) r
¨
θ − rω
2
0
sin θ = 0, (b)
˙
θ = ω
0
,
(c) F
r
=
1
2
mrω
2
0
Chapter 2
2.1. (a) m
¨
x = 2xλ, m
¨
y + mg =
8
3
yλ
(b) x
max
= 0.9063L , P = 1.077mg
2.2. (a) m(2
¨
x −l
¨
φ sin φ − l
˙
φ
2
cos φ) =∓µmg sin φ
m(2
¨
y +l
¨
φ cos φ − l
˙
φ
2
sin φ) =±µ mg cos φ
ml(l
¨
φ −
¨
x sin φ +
¨
y cos φ) = 0or
ml
2
2
¨
φ =∓
1
2
µmgl
(b) |(
˙
x cos φ +
˙
y sin φ)
˙
φ| >µg
2.3. (a) m
¨
x = 2xλ, m
¨
y =−λ − mg,
¨
x =−
2x
4x
2
+ 1
(2
˙
x
2
+ g)
(b)
˙
x =−
2g
x
2
0
− x
2
4x
2
+ 1
2.4. (a)
˙
φ =
1 +
2r
L
cos φ +
r
2
L
2
ω,(b)
˙
θ =
1 +
r
2
l
2
ω
2.5. (a) m(L cos φ − Rθ)
¨
θ − mR
˙
θ
2
− 2mL
˙
θ
˙
φ sin φ = 0
mL
2
¨
φ + mL
˙
θ
2
(L cos φ − Rθ ) sin φ − mgL cos φ = 0
(b) F = m[L
˙
φ
2
+ (L cos φ − Rθ )
˙
θ
2
cos φ + g sin φ]
2.6. (a) mR
2
¨
θ + mR
2
(
˙
φ + )
2
sin θ cos θ + cR
2
˙
θ = 0
mR
2
¨
φ cos
2
θ − 2mR
2
(
˙
φ + )
˙
θ sin θ cos θ + cR
2
˙
φ cos
2
θ = 0

404 Appendix
2.7. m
2
¨
x −
l
√
2
¨
φ(sin φ + cos φ) +
l
˙
φ
2
√
2
(sin φ − cos φ)
=−λ sin φ
m
2
¨
y +
l
√
2
¨
φ(cos φ − sin φ) −
l
˙
φ
2
√
2
(sin φ + cos φ)
= λ cos φ
ml
l
¨
φ −
¨
x
√
2
(sin φ + cos φ) +
¨
y
√
2
(cos φ − sin φ)
= 0
2.8. m[2
¨
x −(l
o
+ s)
¨
φ sin φ +
¨
s cos φ − (l
0
+ s)
˙
φ
2
cos φ − 2
˙
φ
˙
s sin φ] =−λ sin φ
m[2
¨
y + (l
0
+ s)
¨
φ cos φ +
¨
s sin φ − (l
0
+ s)
˙
φ
2
sin φ + 2
˙
φ
˙
s cos φ] = λ cos φ
m[(l
0
+ s)
2
¨
φ − (l
0
+ s)
¨
x sin φ + (l
0
+ s)
¨
y cos φ + 2(l
0
+ s)
˙
φ
˙
s] = 0
m[
¨
s +
¨
x cos φ +
¨
y sin φ − (l
0
+ s)
˙
φ
2
] +ks = 0
2.9. (a)
˙
x =
2
3
v
0
,(b)
ˆ
P =
1
3
√
2 mv
0
2.10. (a) 2ml
2
¨
θ
1 −
2
3
sin
2
θ
−
4
3
ml
2
˙
θ
2
sin θ cos θ −
ml
2
ω
2
0
sin θ cos θ
3
1 −
2
3
cos
2
θ
2
= 0
(b)
˙
θ =
1
2
√
3 ω
0
2.11. mr
¨
θ − mr
2
sin θ cos θ + µ
N
2
r
+ N
2
φ
sgn(
˙
θ) = mg sin θ
where N
r
=−m(r
˙
θ
2
+r
2
sin
2
θ) +mg cos θ
N
φ
= 2mr
˙
θ cos θ
2.12. (a) ml
2
¨
θ − ml
2
(
˙
φ + ω)
2
sin θ cos θ − mRlω
2
cos θ cos φ + mgl sin θ = 0
ml
2
¨
φ sin
2
θ + 2ml
2
˙
θ(
˙
φ + ω) sin θ cos θ + mRlω
2
sin θ sin φ = 0
(b) E =
1
2
ml
2
(
˙
θ
2
+
˙
φ
2
sin
2
θ) −
1
2
mω
2
(R
2
+l
2
sin
2
θ + 2Rl sin θ cos φ)
−mgl cos θ
2.13. (a)
˙
x =
˙
x
0
,
˙
y = v
0
(b) T
2
=
1
2
mv
2
0
,
T =
1
2
mv
2
0
+ mx
0
v
0
,(c)
ˆ
C = mv
0
j
2.14. (a) m
¨
r − mr
˙
θ
2
= λ, mr
2
¨
θ + 2mr
˙
r
˙
θ =−kλ
(b)
˙
r =
kv
0
√
r
2
+ k
2
, N =
(r
2
+ 2k
2
)mv
2
0
(r
2
+ k
2
)
3/2
(c)
¨
r =−
r
˙
r
2
r
2
+ k
2
−
µ
˙
r
2
(r
2
+ 2k
2
)
k(r
2
+ k
2
)

405 Answers to problems
2.15. (a)
¨
x =
1
l
2
[g(µ(x
2
− y
2
) +(1 − µ
2
)xy) − (x −µy)(
˙
x
2
+
˙
y
2
)] −µg
¨
y =
1
l
2
[g(y + µx)
2
− (y + µx)(
˙
x
2
+
˙
y
2
)] − g
(b)
¨
θ =
g
l
[(1 −µ
2
) sin θ − 2µ cos θ] + µ
˙
θ
2
2.16. (a) 2m
¨
r
1
− 2mr
1
˙
θ
2
= r
1
λ, 2m
¨
r
2
− 2mr
2
˙
θ
2
= r
2
λ, 2ml
2
¨
θ = 0
¨
r
1
+
r
1
l
2
−r
2
1
˙
r
2
1
= 0,
¨
r
2
+
r
2
l
2
−r
2
2
˙
r
2
2
= 0,
¨
θ = 0
(b) r
1
= l sin
√
2 v
0
t
l
+
π
4
, r
2
= l cos
√
2 v
0
t
l
+
π
4
,θ= ω
0
t
2.17. (a) At t = 0,
ˆ
C
r
= mv
0
.Att = R/v
0
,
ˆ
C
r
=−mv
0
(b) v =
1
2
Rω
0
,(c)W =
1
2
mv
2
0
(first impulse)
W =−
1
2
mv
2
0
(second impulse), W =−
3
8
mR
2
ω
2
0
2.18. (a)
√
3 sin θ
1
− sin θ
2
= 0
(b) T =
(3 −sin
4
θ
2
)
2(3 −sin
2
θ
2
)
ml
2
˙
θ
2
2
, V = mgl (cos θ
2
+
3 −sin
2
θ
2
)
(c) v
B
= 1.0824
√
gl downward, (d)
¨
y
A
= 2(
√
2 − 1)g
2.19. (a)
ˆ
N = 4mv
0
,
˙
θ(0+) =
˙
φ(0+) =−
v
0
l
˙
x(0+) = 0,
˙
y(0+) =
1
3
v
0
,
θ,φ,x, y unchanged
(b) 2ml
2
¨
θ
1 −
2
3
sin
2
θ
−
4
3
ml
2
(
˙
θ
2
+
˙
φ
2
) sin θ cos θ = 0
2ml
2
¨
φ
1 −
2
3
cos
2
θ
+
8
3
ml
2
˙
θ
˙
φ sin θ cos θ = 0
(c) θ
min
= 0,
˙
φ =−
2v
0
l
2.20. (a)
¨
x = 0,
¨
y = 0,
¨
θ = 0,
¨
φ = 0
(b) F
AB
= F
CD
=
1
2
ml(
˙
θ
0
−
˙
φ
0
)
2
, F
AD
= F
BC
=
1
2
ml(
˙
θ
0
+
˙
φ
0
)
2
(c) Period = π/
˙
φ
0
2.21. (a)
ml
2
2
¨
θ(1 +cos
2
θ) +
1
2
ml
2
(
˙
φ
2
−
˙
θ
2
) sin θ cos θ + mgl cos θ = 0
ml
2
2
¨
φ cos
2
θ − ml
2
˙
θ
˙
φ sin θ cos θ = 0
406 Appendix
(b)
˙
θ =−
1
8
˙
φ
2
0
+
√
2
g
l
(c) |
˙
φ
0
|
min
= 2.3784
g
l
2.22. (a) (2 sin
2
θ + 1)
¨
θ + 2
˙
θ
2
sin θ cos θ +
g
2r
cos θ = 0
(b) θ = 28.26
◦
, (c) v
2
= 0.4608
√
gr
Chapter 3
3.1. (a) ω =
√
3
20
J +
1
20
K =
√
3
20
j −
1
20
k (b) C =
10 0
0
1
2
√
3
2
0 −
√
3
2
1
2
˙
C =
0
1
20
−
√
3
20
1
20
00
√
3
20
00
3.2. [(I
xx
sin
2
ψ + I
yy
cos
2
ψ) sin
2
θ + I
zz
cos
2
θ]
¨
φ +(I
xx
− I
yy
)
¨
θ sin θ sin ψ cos ψ
+ I
zz
¨
ψ cos θ + [2(I
xx
sin
2
ψ+ I
yy
cos
2
ψ) sin θ cos θ − 2I
zz
sin θ cos θ ]
˙
φ
˙
θ
+ 2(I
xx
− I
yy
)
˙
φ
˙
ψ sin
2
θ sin ψ cos ψ + (I
xx
− I
yy
)
˙
θ
2
cos θ sin ψ cos ψ
+ [(I
xx
− I
yy
) sin θ(cos
2
ψ − sin
2
ψ) − I
zz
sin θ]
˙
θ
˙
ψ = Q
φ
(I
xx
cos
2
ψ + I
yy
sin
2
ψ)
¨
θ + (I
xx
− I
yy
)
¨
φ sin θ sin ψ cos ψ
− (I
xx
sin
2
ψ + I
yy
cos
2
ψ − I
zz
)
˙
φ
2
sin θ cos θ
+ [(I
xx
− I
yy
)(cos
2
ψ − sin
2
ψ) + I
zz
]
˙
φ
˙
ψ sin θ
− 2(I
xx
− I
yy
)
˙
θ
˙
ψ sin ψ cos ψ = Q
θ
I
zz
¨
ψ + I
zz
¨
φ cos θ − (I
xx
− I
yy
)
˙
φ
2
sin
2
θ sin ψ cos ψ
− [(I
xx
− I
yy
)(cos
2
ψ − sin
2
ψ) + I
zz
]
˙
φ
˙
θ sin θ
+ (I
xx
− I
yy
)
˙
θ
2
sin ψ cos ψ = Q
ψ
3.3. (a) v
1
=
v
0
√
2
i +
1 −e
2
j
, v
2
=
1 +e
2
√
2
v
0
j
(b) v
1
=
v
0
√
2
1 −
1 +e
2
µ
i +
1 −e
2
j

407 Answers to problems
v
2
=
v
0
2
√
2
(1 +e)(µi + j)
ω
1
= ω
2
=
1 +e
2
√
2 I
µrmv
0
k
3.4. (a) ω
x
=
5M
y
4I
t
1 −cos
4
5
t
,ω
y
=
5M
y
4I
t
sin
4
5
t
(b) t = 10π/
3.5. (a)
˙
ψ =−H
sin
2
φ
I
yy
+
cos
2
φ
I
zz
˙
θ = H
1
I
zz
−
1
I
yy
cos θ sin φ cos φ
˙
φ = H
1
I
xx
−
sin
2
φ
I
yy
−
cos
2
φ
I
zz
sin θ
(b)
˙
ψ =−
H
I
t
,
˙
θ = 0,
˙
φ = H
1
I
a
−
1
I
t
sin θ
3.6. (a)
3
2
m + m
0
¨
x
1
+
1
4
m
¨
x
2
= F,
3
2
m + m
0
¨
x
2
+
1
4
m
¨
x
1
= 0
(b) x
2
=−
1
14
, (c) P
1
=−
11
195
F (upper face), P
2
=
3
195
F (lower face)
3.7. (a) ω
x
=
123
190
ω
0
,ω
y
=
12
95
ω
0
,ω
z
=
21
190
ω
0
(b) T = 0.9711 ma
2
ω
2
0
3.8.
˙
ψ =±
&
'
'
(
mgr tan θ
R
r
I
a
+ I
t
sin θ + mRr
3.9. (a) m
¨
x +mr
¨
θ − mx
˙
θ
2
− mg sin θ = 0
m
r
2
+ x
2
+
l
2
12
¨
θ + mr
¨
x +2mx
˙
x
˙
θ − mg
(
r sin θ + x cos θ
)
= 0
3.10. (a) I
t
¨
θ − I
a
˙
φ sin θ − I
t
˙
φ
2
sin θ cos θ + mgl sin θ = 0
I
t
¨
φ sin θ + 2I
t
˙
θ
˙
φ cos θ + I
a
˙
θ = 0
(b) θ
min
= 34.63
◦
3.11. (a) (I
a
sin
2
θ + I
t
cos
2
θ)
¨
ψ − I
a
¨
φ sin θ = Q
ψ
= 0
I
a
(
¨
φ −
¨
ψ sin θ ) = I
a
˙
= Q
φ
(b) Q
φ
is internal.

408 Appendix
3.12.
2mR
2
sin
2
θ +
1
2
ml
2
(sin
2
θ sin
2
ψ + cos
2
θ)
¨
φ
+
1
2
ml
2
¨
θ sin θ sin ψ cos ψ +
1
2
ml
2
¨
ψ cos θ
+ (4mR
2
− ml
2
cos
2
ψ)
˙
φ
˙
θ sin θ cos θ +
1
2
ml
2
˙
θ
2
cos θ sin ψ cos ψ
+ ml
2
˙
φ
˙
ψ sin
2
θ sin ψ cos ψ − ml
2
˙
θ
˙
ψ sin θ sin
2
ψ = 0
2mR
2
+
1
2
ml
2
cos
2
ψ
¨
θ +
1
2
ml
2
¨
φ sin θ sin ψ cos ψ
−
2mR
2
−
1
2
ml
2
cos
2
ψ
˙
φ
2
sin θ cos θ + ml
2
˙
φ
˙
ψ sin θ cos
2
ψ
− ml
2
˙
θ
˙
ψ sin ψ cos ψ + 2mgR sin θ = 0
1
2
ml
2
¨
ψ +
¨
φ cos θ −
˙
φ
2
sin
2
θ sin ψ cos ψ +
˙
θ
2
sin ψ cos ψ
− 2
˙
φ
˙
θ sin θ cos
2
ψ
= 0
3.13.
˙
x =
˙
x
0
,
˙
y =
12a
2
˙
y
0
+ al
2
ω
0
12a
2
+l
2
,ω=
12a
˙
y
0
+l
2
ω
0
12a
2
+l
2
3.14. (a)
¨
θ =
12
ml
2
(1 +3 sin
2
θ)
12β
2
cos θ
ml
2
sin
3
θ
−
ml
2
4
˙
θ
2
sin θ cos θ +
mgl
2
sin θ
where β =
ml
2
12
˙
φ(0) sin
2
θ(0) =
ml
2
24
ω
0
(b) N =−
mlω
2
0
10
√
2
+
2
5
mg
3.15. (a) (I
t
+ ml
2
cos
2
θ)
¨
θ − ml
2
˙
θ
2
sin θ cos θ + I
t
˙
ψ
2
sin θ cos θ + I
a
˙
ψ cos θ
=−mgl cos θ
I
t
¨
ψ cos θ − 2I
t
˙
θ
˙
ψ sin θ − I
a
˙
θ = 0
(b) θ
min
= 30
◦
,(c)
˙
ψ =−2
2g
l
3.16. (a) T =
1
2
(3m + m
0
)v
2
+
1
2
mr
2
2
+
3
4
mL
2
+
m
0
L
2
12
˙
φ
2
m =
(3m + m
0
)0
0
mr
2
2
+
3
4
mL
2
+
m
0
L
2
12
(b) v =
ˆ
F
3m + m
0
,
˙
φ =
ˆ
Fc
mr
2
2
+
3
4
mL
2
+
m
0
L
2
12
