Amaro A., Reed D., Soares P. (editors) Modelling Forest Systems

Подождите немного. Документ загружается.

06Amaro Forests - Chap 05 25/7/03 11:05 am Page 56

56 M. Hauhs et al.

computation. ‘Lazy evaluation’ describes the attitude of practical silviculture

towards stand growth quite well (Leibundgut, 1978), even including some of the

prejudices acquired in the scientiﬁc study of forest growth.

Currently the empirical models of forest growth seem to match the needs of

such a ‘lazy evaluation’ task much better than pr

ocess-based models. We suggest

that testing of an interactive approach in forestry may even become a paradigmatic

case in ecosystem modelling, mainly because the empirical basis for management

decisions is so well documented and provides stark contrast to the (surprisingly)

weak performance of process-based models in this application area. Process-based

models typically leave few options for adjusting predictions as new data about the

actual growth responses become available. The preference of silvicultural practition-

ers for empirical over process-based models may thus be rooted in the distinction

that only the former can currently be included easily into interactive management

schemes, while the latter conceptually enforces an attitude towards the forest similar

to that towards the weather and weather predictions.

The example of chess games (interaction based on cultural memory)

demon-

strates the potential roles of theory and modelling in situations where interactive

computing (the game as it is played out) can be distinguished from algorithmic

computing, i.e. with each single decision leading to a next move. This corresponds

to the implicit and ultimate promise of many process-level models for forest growth.

In the case when a realistic state presentation of the stand growth dynamics process

can be found, predictions become feasible and their precision would be limited only

through uncertainties about initial or future boundary conditions (Lange, 1999). The

empirical traditions and heuristics of practical decisions so prominent in silviculture

would be outcompeted and forestry as an ‘art’ or ‘game’ would cease to exist in a

similar manner to which chess would cease to exist with the knowledge of a practi-

cally relevant winning strategy.

What, however, would happen, if our universe is too small, too short lived, or we

e too impatient to wait for a winning strategy in chess to be discovered if it exists; or

if our forests are too complicated and the biotic interaction among trees too history-

dependent for a realistic description by a process model to be invented/discovered in

science? In this case, the only way to become a good chess player is to resort to experi-

enced players and to study played-out games. A master player’s expertise seems

largely to rest on fast access to an archive of played-out games in his/her brain

(Ognjen et al., 2001). When this analogy is taken back to forestry, the only way to deal

with novel goals and novel boundary conditions for forest ecosystems is to update

and improve the practical expertise gained from interaction and to study successfully

managed forests in the past and present. Hence the potential need and impact for

interactive models would be large for forestry in central Europe, where a range of new

boundary conditions devaluates the heuristic basis of silviculture and a large but

hitherto poorly documented archive of played-out games exists only within experts’

memories. A crucial difference from the chess example, however, is that in silviculture

the rules or even the goals of the game are changed ‘on the ﬂy’ as hidden behavioural

phenotypes of trees may be evoked by the new boundary conditions (e.g. increasing

atmospheric CO

levels) or new priorities, such as biodiversity, appear on the political

agenda.

The problem of silvicultural choice does not reduce to the question of whether

and when somebody acts pr

operly as a scientist or as a forest manager, but the issue

This is cultural interaction even though sometimes played by machines. Hence the internal

conﬁgurations or mechanisms do not matter for the type of interaction. Its classiﬁcation focuses on

behaviour only. This example is also discussed by Dreyfus and Dreyfus (1988) and Flyvbjerg (2002).

06Amaro Forests - Chap 05 25/7/03 11:05 am Page 57

57 Algorithmic and Interactive Stand Growth Modelling

is whether interaction can be abstracted out of a given problem in forest manage-

ment or in growth modelling. If we take thinning schemes as an example, the task is

the reconstruction of a speciﬁc growth process in which biological and human inter-

action did take place. As interaction is deﬁned through the external relationship of a

process, the focus in modelling shifts from the search for a realistic representation of

the forest stand itself to a useful representation of an external interface. In particular

the role of visualization is altered to an input interface (Hauhs et al., 1999, 2001). As

an illustrative example we use ﬂight simulators.

Flight simulators are not intended

to represent a plane as such, only its behaviour during its operation as it appears to

a pilot. It is another example where software engineering is providing an ongoing

service rather than transforming static input to output.

In forestry this concept takes on the character of an inverse ﬂight simulator or the

task of inverse engineering of such a pr

ogram. Can we design the behavioural interface

to a simulated forest in such a way that an interactive visualization will be accepted by

experts in silviculture? Such an approach consists of two steps: ﬁrst, an interactive

growth simulator needs to be set up on the basis of the available observations. This ﬁrst

step does not differ from a conventional calibration exercise. Its result is typically non-

unique. The reason is that (for all practical purposes) the set of observations is not large

enough to uniquely identify all the parameters of a process-level model. Therefore the

resulting calibrated models may still contain many ad hoc decisions that will lead to

unreliable predictions. The calibration exercise of this ﬁrst step deﬁnes the initial state

for the subsequent interaction process. In our example, it simulated a given forest stand

up to the age of the ﬁrst thinning.

The second step consists of an interactive selection of that model behaviour that

best r

esembles the (subjective) memories by which an experienced forester describes

the responses of a thinned stand to his interference. The advantage of this coupling

of two steps is that interactive selection appears theoretically more powerful than

(non-interactive) algorithmic selection of data (Goldin and Keil, 2001). The disad-

vantage is that the reference point for successful modelling is shifted to the pool of

expert knowledge in the respective realm. Without such experts, who remember and

are able to agree upon proper growth behaviour and set a standard for reconstruc-

tions, the interactive model would be of no help, i.e. prediction would remain as

elusive as before. However, if there is a group of experts that has something to say

about a silvicultural problem, the model may greatly support and facilitate commu-

nication within this group of experts. To return to the ﬂight simulator metaphor, if

good pilots approve of a simulator, it can be used to pass their expertise on to

novices and ultimately to serve as a communication tool among the experts

themselves.

An Interactive Model Applied to a Thinning Trial at Denklingen (Bavaria)

We illustrate this approach with a well-documented stand from Denklingen (Bavaria).

The Denklingen Norway spruce (Picea abies Karst.) thinning trial was situated on a

glacial moraine in southern Bavaria. It is one of several trials started in the 1880s. At the

time of its harvest in 1991 (due to stormfelling), it had become one of the oldest

Norway spruce thinning trials and had accumulated the longest record from such trials

in Bavaria (H. Pretzsch, personal comunication). It consisted of three treatments, all of

which received a periodic low-thinning regime, although with varying intensity. In the

J.K. Vanclay has already proposed this analogy before, as was pointed out to us by Paul van Gardingen.

06Amaro Forests - Chap 05 25/7/03 11:05 am Page 58

58 M. Hauhs et al.

A-grade condition, only those trees were removed that were expected to die within

the next growth period. B-grade consisted of moderate and C-grade of heavy thin-

ning (late 19th century deﬁnitions).

As a model we use the individual tree simulator

TRAGIC++ described elsewhere

(Hauhs et al., 1995). It allows us to specify a local and variable nutrient supply for

one (growth-limiting) nutrient for which roots compete and the photosynthetic

capacity of leaves competing for light interception. An important feature of this

model is that any stand has to be started from seeds, plants or natural regeneration

for which no or a narrow distribution of initial heights is speciﬁed. Here we started

with identical trees representing the 1.4 × 1.4 m plantation from 1848. The simulated

distributions in height, biomass, diameter, etc. are consequences of competition

between individual trees (algorithmic part) and, in addition (interactive part), the

external interferences imposed by the thinning regimes (Hauhs et al., 2001).

The Denklingen A-grade data set comes closest to the concept of an

autonomous gr

owth process not impacted by management. That is why we used it

here for the ﬁrst of the two steps outlined above. From the plantation of identical

trees the model is able to match observed distributions of height and diameter mea-

surements for 108 years between the ages of 35 (when measurements started) and

143 (the last recording before the stand was felled by a storm). We found several

parameterizations of this model in which the number of trees and the averages for

height diameter and basal area are relatively close to observations. It is difﬁcult for

such a multi-dimensional calibration exercise to deﬁne a criterion for the best ﬁt

(Fig. 5.1). In addition, a highly parameterized model such as

TRAGIC++ gives typi-

cally non-unique results in a calibration exercise.

This is the point where interactive selection provides a further and reﬁned test-

ing possibility for the several, equally satisfactory

, calibrations of a process-based

model. Any calibrated reconstruction of the A-grade can be taken as the non-interac-

tive growth part behind the responses observed in the thinned variants B- and

C-grades. An experienced forester is asked to select the trees in each thinning event

based on the visualization of the simulated reconstruction (Fig. 5.2). In addition, one

might provide the forester with the explicit list of felled trees with diameter and

height, or alternatively just with the total basal area of the trees taken out in each

thinning (a much more realistic constraint in terms of operational forestry).

The forester is confronted with this image and asked whether the presented for-

est is acceptable as a plausible thinning task and, if yes, the thinning can be imposed

interactively at the tr

ee level through the visual interface. After completing this thin-

ning the resulting stand structure is passed back to the autonomous growth part of

the model (

TRAGIC++). That is how the algorithmic part of the simulation is extended,

say for the next 10–20 years. The forester is then asked again whether he or she

accepts the resulting visualized stand as a plausible result of the preceding actions

and, if yes, continues with the thinning exercise. Whenever the model response is

judged as unrealistic, the forester has the option of a restart with a slightly changed

set of behavioural tree rules or a slightly changed nutrient availability, etc.

We will not present results of such trials with experts here, as we want only to

point out how this can be organized and the new role that forest growth models

would play in this interactive task, which eventually becomes a communication

process. The current best calibration of the A-grade is accessible through a graphical

For a technical description of the current version see: www.bitoek.uni-bayreuth.de/mod/html/

tragic/documentation/documentationnotes.pdf

Currently this step will not happen automatically, a user has to mail the database administrator for this

request.

06Amaro Forests - Chap 05 25/7/03 11:05 am Page 59

Algorithmic and Interactive Stand Growth Modelling

Mean height

Mean diameter at breast height

/ha

0 25 50 75 100 125 150 0 25 50 75 100 125 150

Stand age

real

sim.

Stand age

160

4000

Basal area

140

3500

rees

120

100

Number/ha

3000

2500

2000

1500

1000

500

0 25 50 75 100 125 150 0 25 50 75 100 125 150

Stand age Stand age

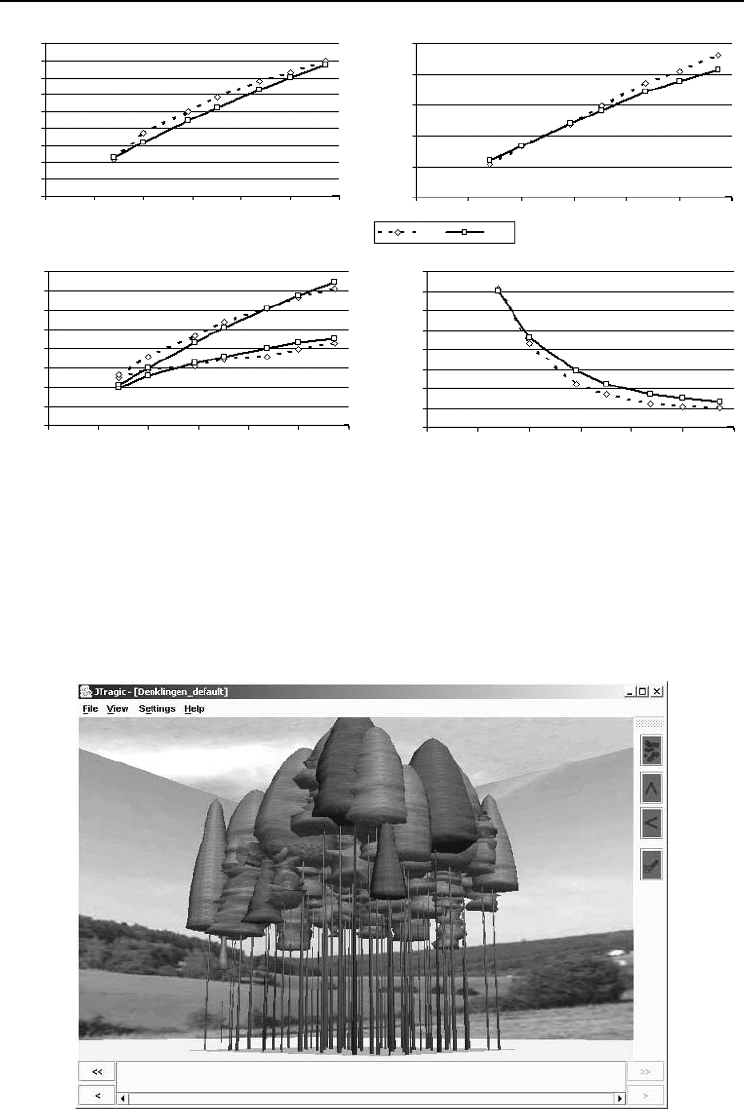
Fig. 5.1. The results of a TRAGIC++ calibration (squares) to the Denklingen A-grade data set (diamonds). The

stand was planted as 5000 identical seedlings per hectare and then run with constant boundary conditions

and without any interference for 143 years. Mortality up to age 40 is entirely due to competition among

trees. After age 40 a random mortality of 0.5%/year has been added. The trees randomly removed by this

procedure are larger than the trees selected by the (interactive) low-thinning regime that was applied at the

real stand. This caused the tree number towards the end of the run to be higher and diameter to be lower in

the simulation. This deviation has been accepted as we wanted to see how closely the model can match

observations in the non-interactive mode. Shown are averages from ﬁve runs over a 50 × 50 m section with

yearly time steps. The standard deviation is about ±3% and is not shown.

Fig. 5.2. A typical screenshot from an interactive session using the graphical interface JTRAGIC. The shown

stand simulates a 20 × 20 m section of the reconstructed A-grade Denklingen stand at the age of 60 years

due for thinning.

06Amaro Forests - Chap 05 25/7/03 11:05 am Page 60

60 M. Hauhs et al.

interface, JTRAGIC, where interested readers can place their own thinning attempts

(www.bitoek.uni-bayreuth.de/mod/html/webapps).

It is necessary, however, to start this selection with experts only, because we

want to exclude the possibility that the model was discar

ded due to a thinning

choice imposed by a silviculturally incompetent user. The main question becomes:

Are there models that are suitable to be accepted by such experts as a proper docu-

mentation and repository of their decisions, as these reside in their subjective mem-

ories? To what extent can these reconstructions be kept consistent with the objective

(non-interactive) observations of such a stand?

Discussion and Outlook

Computation has become a powerful tool in the automatic generation of complex

patterns from simple iterated functions. One prominent example is the implementa-

tion of grammars such as L-systems in which modular organisms can be generated

from the typical building blocks. The architecture of a tree can be algorithmically

derived from a set of modules and rules. When linked with a powerful visualization

software, such programs have come close to photo-realism in presenting individual

plants (Prusinkiewicz and Lindenmayer, 1990; Godin, 2000; see also Knauft, Chapter

30, this volume).

This phase of autonomous growth of a stand can be extended when the (seem-

ingly) interactive aspects can be r

educed to an algorithmic function. For example,

interactive competition among trees for photosynthetically active radiation can be

explicitly calculated from a simpliﬁed light extinction function and the actual verti-

cal distribution of above-ground biomass of the stand. It is here that currently much

of the computational power of IT has been allocated in forest growth modelling.

This rigorous, but still unsuccessful, approach in terms of convincing forest man-

agers, represents the ‘brute force’ method, as additional resources of computing are

entirely directed towards an extension of existing algorithmic tasks.

The interactive approach proposed here is motivated by the observation that

interactive selection among an immense number of choices is in many r

eal life situa-

tions more powerful than an algorithmic selection. For example, in the world of cul-

tural interaction, (interactive) job interviews, where the next question depends on

the previously given answers, are obviously more powerful than questionnaires

(where the sequence of answering is not prescribed). At the biological level of inter-

action as observed in ecosystems, the interactive nature of living organisms may

itself be an irreducible feature (Hauhs and Lange, 2003). Past attempts to get rid of

this feature have more often been motivated by its incompatibility with the prevail-

ing paradigm of process-oriented modelling rather than by a proper abstraction of

ecosystem behaviour. Here we propose to utilize the additional classiﬁcatory power

of interaction for a faster and more complete (in terms of the available sources of

knowledge) zoom on to consistent growth reconstructions.

An expansion of forest growth modelling has been sketched from serving pre-

dictive tasks based on algorithmic modelling towar

ds also serving communicative

tasks based on interactive modelling. This proposed change moves the focus in

stand modelling from the search for a realistic representation of stand dynamics to

the support of the documentations of silvicultural experience; in the words of our

examples, creating an archive of played-out games as remembered by experts rather

than looking further for a winning strategy for the whole game.

Human beings are (still) superior to computers in the area of pattern r

ecognition,

in fact this is the reason why humans are still able to beat a computer at chess.

06Amaro Forests - Chap 05 25/7/03 11:05 am Page 61

61 Algorithmic and Interactive Stand Growth Modelling

Computers are much more powerful in pattern generation. A proper coupling of pat-

tern generation (algorithmic) and pattern selection (interactive, experience-based)

becomes possible if the generated patterns from a computer model can rapidly be

visualized as a virtual forest. An integration between the two perspectives would be

achieved when the unavoidable plasticity of the model (and the range of calibrated

parameter sets) is sufﬁcient to cover the range of expert behaviours encountered in

an interactive session; in addition in such a framework it can be checked whether or

not the subjective judgements of individual experts converge to reproducible and

accepted standards in the ﬁeld. Another potential outcome (although we regard it as

unlikely) is that the approach indicates a lack of any standard among experienced

practitioners. However, in the case where a reproducible pattern or reaction norm

has been found, the scientiﬁc problem can be stated in a new way: What is the

best (simplest) explanation in terms of processes for this reproducible pattern in

silviculture?

We suggest that much more effort can and should be devoted to the problem of

interaction of which silvicultur

e may serve as a paradigmatic example. The ‘should’

is stated from the perspective of a largely empirical management regime that

requires new and appropriate technology for a continuous updating of its expertise

when faced by the changes in its boundary conditions, e.g. in central Europe. The

‘can’ is stated from the perspective of the potential that IT provides for growth mod-

elling. Modelling becomes in this case a predominately backward-oriented exercise

in time, by which valuable data and experiences from the past become more efﬁ-

ciently documented than by books or words. Instead of predictions that substitute

for experience, interactive growth models have the potential to preserve and update

the relevant experience in a transparent and efﬁcient way.

Acknowledgements

This work was supported by the German Ministry of Science and Education (BMBF)

under contract no. PT BEO 0339476 D. The manuscript was prepared during a sabbati-

cal stay of the ﬁrst author at the School of Forestry of the University of Canterbury

(NZ). We thank Hans Pretzsch for providing us with the Denklingen data set.

References

Dreyfus, H. and Dreyfus, S. (1988) Mind Over Machine: the Power of Human Mind and Expertise in

the Era of the Computer. Free Press, New York, 25 pp.

Flyvbjerg, B. (2002) Making Social Science Matter. Cambridge University Press, Cambridge.

Godin, C. (2000) Representing and encoding plant architecture: a review. Annals of Forest

Science 57, 413–438.

Goldin, D. and Keil, D. (2001) Evolution, Interaction, and Intelligence: Congress on

Evolutionary Computation CEC’01, Korea, May 2001. Available at: www.cs.umb.edu/

~dqg/papers/cec01.doc

Goldin, D., Keil, D. and Wegner, P. (2001) An interactive viewpoint on the role of UML. In:

Uniﬁed Modelling Language: Systems Analysis, Design, and Development Issues. Idea Group

Publishing. Available at: www.cs.umb.edu/~dqg/papers/uml.doc

Hauhs, M. and Lange, H. (2003) Virtualities and realities of artiﬁcial life. In: Reuter, H.,

Breckling, B. and Mittwollen, A. (eds) Gene, Bits und Ökosysteme, Theorie in der Ökologie.

P. Lang Verlag, Frankfurt/M.

Hauhs, M., Kastner-Maresch, A. and Rost-Siebert, K. (1995) A model relating forest growth to

ecosystem-scale budgets of energy and nutrients. Ecological Modelling 83, 229–243.

06Amaro Forests - Chap 05 25/7/03 11:05 am Page 62

62 M. Hauhs et al.

Hauhs, M., Dörwald, W., Kastner-Maresch, A. and Lange, H. (1999) The role of visualization in

for

est growth modelling. In: Amaro, A. and Tomé, M. (eds) Empirical and Process-based

Models for Forest Tree and Stand Growth Simulation. Edições Salamandra, Lisbon, pp.

403–418.

Hauhs, M., Lange, H. and Kastner-Maresch, A. (2001) Complexity and simplicity in ecosys-

tems: the case of forest management. InterJournal for Complex Systems 415, 1–8 (www.

interjournal.org).

Lange, H. (1999) Are ecosystems dynamical systems? International Journal of Computing

Anticipatory Systems 3, 169–186.

Leibundgut, C. (1978) DieWaldpﬂege. Haupt Verlag, Bern.

Levy, D. and Newborn, M. (1991) How Computers Play Chess. W.H. Freeman, New York.

Ognjen, A., Riehle, H.J., Fher, T., Wienbruch, C. and Elbert, T. (2001) Pattern of y-bursts in chess

players. Nature 412, 603–604.

Pigliucci, M. (2001) Phenotypic Plasticity, Beyond Nature and Nurture. Johns Hopkins University

Press, Baltimore, Maryland.

Prusinkiewicz, P. and Lindenmayer, A. (1990) The Algorithmic Beauty of Plants. Springer, New

York.

Schanz, H. (1995) Forstliche Nachhaltigkeit. Befragung zum Begriffsverständnis der Forstleute

in Deutschland. Allgemeine Forstzeitschrift 50(4), 188–192.

Stein, L.A. (1999) Challenging the computational metaphor: implications for how we think.

Cybernetics and Systems 30 (6), September 1999.

Vanclay, J.K. and Skovsgaard, J.P. (1997) Evaluating forest growth models. Ecological Modelling

98, 1–12.

van Leeuwen, J. and Wiedermann, J. (2001) Beyond the Turing limit: evolving interactive sys-

tems. In: Pacholski, L. and Ruzicka, P. (eds) SOFSEM 2001: Theory and Practice in

Informatics, Proceedings of the 28th conference, Lecture Notes in Computer Science Vol.

2234. Springer-Verlag, Berlin, pp. 90–109.

Wegner, P. (1997) Why interaction is more powerful than algorithms. Communication Association

Computing Machinery 40(5).

Wegner, P. and Goldin, D. (2003) Computation beyond Turing machines. Communication

Association Computing Machinery (in press).

07Amaro Forests - Chap 06 25/7/03 11:05 am Page 63

6 Linking Process-based and

Empirical Forest Models in

Eucalyptus Plantations in Brazil

Auro C. Almeida,

1,2

Romualdo Maestri,

Joe J. Landsberg

and José R.S. Scolforo

Abstract

The 3-PG model (Landsberg and Waring, 1997) was parameterized to predict potential produc-

tivity across 170,000 ha of Eucalyptus grandis hybrid plantation distributed in 19 regions in east-

ern Brazil. The regions were deﬁned on the basis of meteorological measurements made by

automatic weather stations. Mean annual increments estimated by the model for a 6-year rota-

tion were compared with available observations made annually in permanent sample plots

(PSPs). The goodness of ﬁt between estimated and observed growth was determined by R

0.92. Comparisons between model estimates and measurements such as basal area and total

volume are presented.

An empirical model called E-GROW ARCEL was developed and ﬁtted using PSP data from

the same region. The model is based on recovering the parameters of the Weibull probability

density function by matching their moments to estimated stand level variables. Stand models

were ﬁtted for projections of stand basal area, mortality, dominant height, tree height, DBH

(diameter at breast height) variance and stem taper. Volume of log types in the DBH distribu-

tion can be estimated.

Mean annual increment (MAI), one of the outputs of 3-PG, was used to establish a hybrid

approach, linking the two models by matching the relationship between MAI and site index

from E-GROW ARCEL. Growth curves and yields are generated.

The hybrid approach is being established as a basis for decision making and management

of fast-growing E. grandis hybrid plantations in eastern Brazil.

Introduction

The area of fast growing eucalyptus plantations in Brazil has been increasing during

the last 20 years. According to the Brazilian Silvicultural Society (SBS, 2001), planted

forest in Brazil in 2000 was estimated at 4.8 million ha; these plantations are the

basis for the pulpwood industry in Brazil. Its high productivity is a result of ideal

Aracruz Celulose S.A., Brazil

Correspondence to: aca@aracruz.com.br or rmaestri@aracruz.com.br

The Australian National University, School of Resources Environmental and Society, Australia

Universidade Federal de Lavras, Brazil

07Amaro Forests - Chap 06 25/7/03 11:05 am Page 64

64 A.C. Almeida et al.

climatic conditions, applied research, and improvements in genetics and silvicul-

tural practices. Many forest companies are working with a plantation rotation length

of 6–7 years. With this short rotation, any change in climate, such as severe drought

stress, has direct effects on productivity and wood quality.

Forest resource management requires decisions to be made on the strategy and

tactics of operations.

At all these levels, decision making may be supported by

mathematical models (Hinssen, 1994). Demand for speciﬁc information by forest

managers and planners is one of the reasons for changing this situation and moving

towards a causal-oriented approach. Questions about potential productivity, the

effects of climate on forest growth, and the ability to understand and analyse the

effects of silvicultural practices, such as soil preparation, weed and disease control,

fertilization and water management, can be answered using process-based models

and in some cases integrating these with empirical models in operational systems.

The development of effective and accurate models to predict forest growth and

oducts during the forest rotation is essential for forest managers and planners.

Empirical growth and yield models, which rely on ﬁtting functions to measurement

data from a sample of the forest population of interest (Burkhart, 1997), are the tools

that have mainly been used to provide decision-support information that meets

basic operational needs for evaluating various forest management scenarios

(Mohren and Burkhart, 1994). Growth and yield predictions are used to assess prof-

itability, determine harvesting schedules, estimate site potential and risks involved,

and evaluate silvicultural practices (Dye, 2001).

The development of process-based models to predict forest growth has been

ogressing rapidly in the last few years. However, operational applications in for-

est plantations are still at an early stage. These models focus on the representation

and explanation of the processes that take place in forest ecosystems and highlight

state variables that are closely associated with these processes (Larocque, 1999).

However, despite the logical concepts underlying process-based models, they are

not yet being used as operational tools in forest management; most of them are used

as research tools only. Baldwin et al. (1993), MacLean (1999), Kimmins et al. (1999),

Host et al. (1999), Hauhs et al. (1999) and Battaglia et al. (1999) have recently com-

bined process-based and empirical models. Mäkelä et al. (2000) consider that the

future lies in models that combine biophysical processes and empirical relationships

– referred to as mixed or hybrid models. Interest is being shown, by some forestry

companies, in the use of these models as operational tools (Almeida, 2000).

Our aim in this chapter is to demonstrate the possibility of integrating the

ocess-based model 3-

PG with the empirical growth model called E-GROW ARCEL, to

produce a hybrid model developed and adjusted for Eucalyptus grandis in Brazil. We

used a dense network of measurements of growth rates from permanent plots to

evaluate the model’s performance.

State of the Art

Vanclay (1999) deﬁned stand growth models as abstractions of the natural dynamics

of a forest stand, which may encompass growth, mortality, and other changes in

stand composition and structure. Korzukhin et al. (1996) presented a detailed analy-

sis of the relative merits of process-based and empirical forest models, which high-

lighted the value of both classes of models and indicated how they can be applied in

forest ecosystem management.

Currently available process-based models can provide good estimates of

owth and biomass productivity at various scales; combined with conventional

07Amaro Forests - Chap 06 25/7/03 11:05 am Page 65

65 Linking Process-based and Empirical Models

mensuration-based growth and yield models they can provide information of the

type required by managers and planners (Landsberg, 2003). Some of the most com-

monly cited models in the literature are:

FOREST-BGC (Running and Coughlan, 1988;

Running and Gower, 1991),

CENTURY (Parton et al., 1987), G’DAY (Comins and

McMurtrie, 1993), 3-

PG (Landsberg and Waring, 1997), PROMOD (Battaglia and Sands,

1997),

JABOWA (Botkin et al., 1972) and MAESTRO (Wang and Jarvis, 1990). All these

have been used and tested as research tools in different parts of the world, with data

from a range of environments. Several authors argue that the limited application of

process-based models as practical tools is a consequence of the large number of

parameter values required, the complexity of the models and the lack of appropriate

documentation. However, despite these factors, the use of process-based models

must increase our understanding of the environmental factors affecting growth, and

they can be used to estimate potential productivity in areas without forest and

under changing environmental conditions (Mohren and Burkhart, 1994; Korzukhin

et al., 1996). Models with fewer parameters that express the physiological processes

in simple terms are more likely to be used in forest management.

Empirical growth models may be at different levels of detail (Maestri et al.,

1995). They may be size class models, single-tr

ee models, or apply to a whole stand,

depending on the detail required. These models are derived from tree size data from

stands in a range of ages, site indices (SIs), stand densities and management condi-

tions. They are widely used in forest planning activities. However, they are limited

to be transportable to new areas where no measured growth data are available.

Several studies have been done using empirical growth models that include

envir

onmental variables. Hunter and Gibson (1984) used principal component

analysis (PCA) to select soil characteristics and climatic variables that exerted signif-

icant effects on growth. They observed a positive relationship between SI and rain-

fall, nutrients, topsoil depth and soil penetrability of Pinus radiata stands in New

Zealand. Carter and Klinka (1989) related SI of coastal Douglas-ﬁr stands in British

Columbia to available soil micronutrients and soil water deﬁcits during the growth

season. Snowdon et al. (1998) incorporated climatic indices derived from a process-

based model,

BIOMASS, into an empirical growth model, to describe stand height,

basal area and volume in an initial spacing trial with P. radiata. These indices

improved the ﬁt compared with the basic empirical equations by 13%, 22% and 31%

for mean tree height, stand basal area and stand volume, respectively. Woollons et al.

(1997) incorporated climatic variables into a basal area model of P. radiata in New

Zealand, improving the accuracy of the model by 10%.

A hybrid approach combining the main advantages of process-based and

empirical models has been adopted in some cases. Baldwin et al

. (1993) combined a

single-tree empirical model called

PTAEDA2 (Burkhart et al., 1987) with a process-

based model called

MAESTRO (Wang and Jarvis, 1990). Using PTAEDA2 they projected

to a certain age the stand variables used by

MAESTRO: individual mean crown ratio,

crown shape, crown length, and the vertical and horizontal distributions of foliage

biomass. This information was then used by

MAESTRO to calculate biomass produc-

tion, which was fed back to

PTAEDA2 to adjust its predictions. These steps were

repeated to the end of the rotation.

Battaglia et al.

(1999) used the process-based model PROMOD and the empirical

model

NITGRO developed for Eucalyptus nitens plantations. The resulting hybrid

model was applied in 16 Eucalyptus globulus stands in Tasmania, Australia.

PROMOD

predicted the mean annual increment (MAI, m

/ha/year) and estimated the SI

applying an empirical relationship between MAI and SI.