Ames W.F., Roger C. Nonlinear equations in the applied sciences. Volume 185
Подождите немного. Документ загружается.

410
M.
C.
Nucci
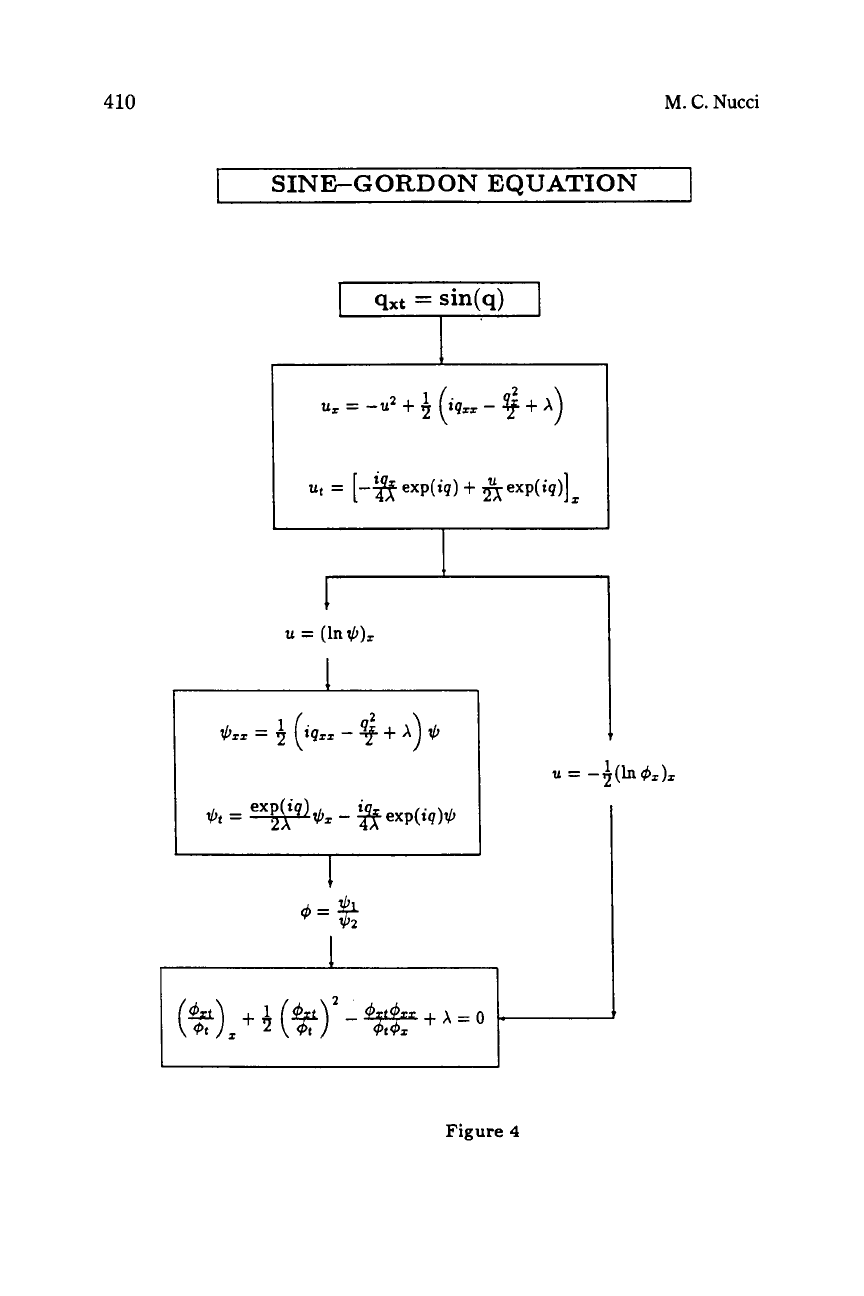
SINE-GORDON
EQUATION
I
Figure
4
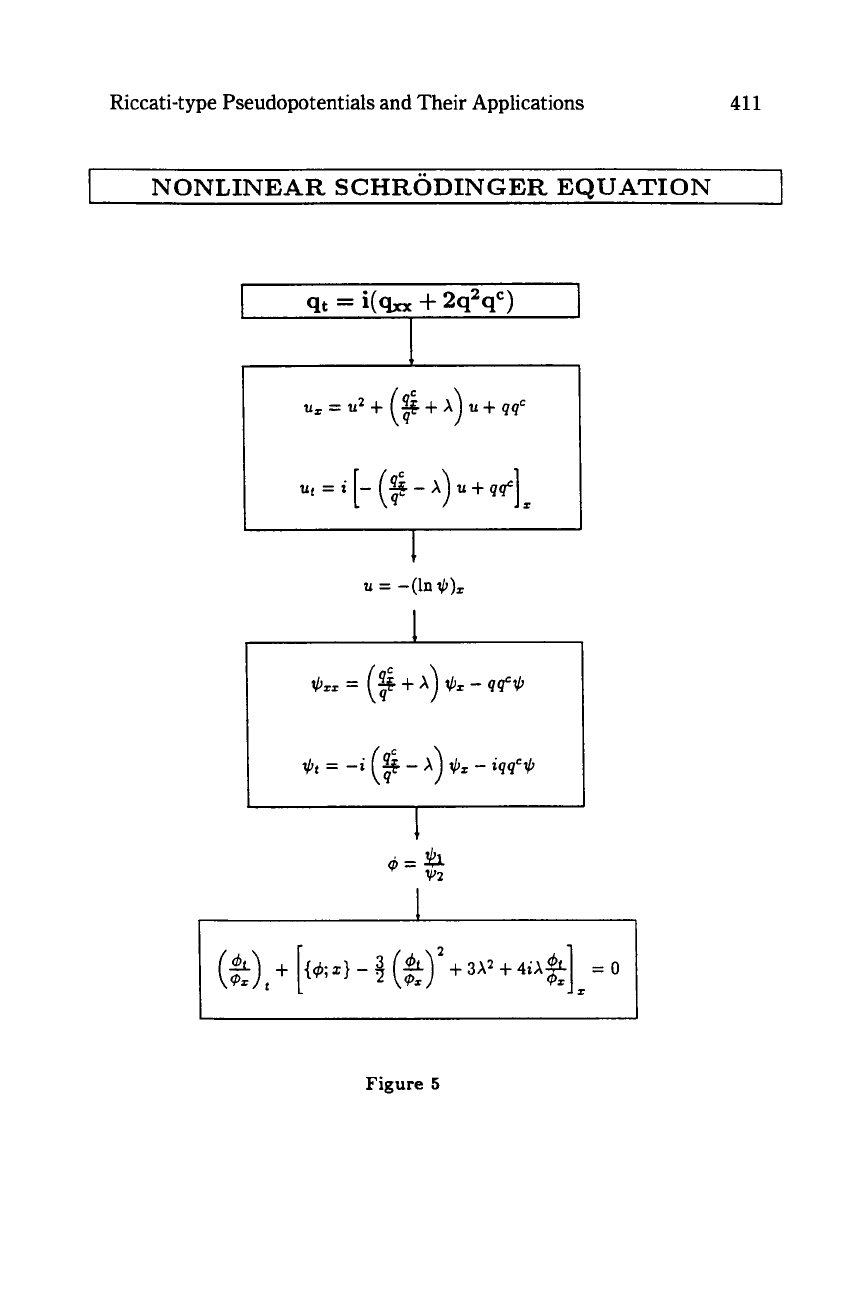
Riccati-type Pseudopotentials and Their Applications
41
1
I
NONLINEAR
SCHRODINGER
EQUATION
u,=uz+
++A
u+qqc
(r
1
ut
=
i
[-
(5
-
A)
u
+
qe]
I
u
=
-(ln
$)I
Figure
5

412
M.
C.
Nucci
2.3
Riccati-chain
In
[3]
the Riccati-chain was given. It
was
noticed that any of its
elements can be linearized. In Table
1
some
of
them are displayed
up to the fourth-order.
T"'
+
4rrt1+
6r2rt
+
3rt2
+
r4
Table
1:
Linear transformation and Riccati-chain.
If
T
=
T(Z)
is
a
solution of any element of the Riccati-chain, the
corresponding linear equation has solution V
=
V(z) (see Table
1)
given by:
T
=
(logv)'
(2.34)
This is the transformation between the Riccati equation:
TI
+
T2
=
P(Z)
(2.35)
and the linear second order equation:
V"
=
P(Z)V
(2.36)
Note that the elements of the Riccati-chain are formally invariant
under the simple transformation
u*
=
-u.
The transformation:
1
2
T
=
--
(log
Wt)l
(2.37)

Riccati-type Pseudopotentials and Their Applications
413
leads to equations involving the Schwarzian derivative, but these
novel equations (order
2
4)
are not invariant under the Mobius
group. In Table 2 the transformation (2.37)
is
applied
to
some ele-
ments of the Riccati-chain up to the fourth-order.
W”
2w’
--
=
T
1
--{w;
2
x}
=
TI
+
T2
I
--
[{w;
2)”
-
2{w; x}{w;
2)’
-
--{w;
.}”+
--{w;
x}2
=
1
3
20”
1
wtt
2
2
wf
4
w’
Table 2: Schwarzian transformation and Riccati-chain.
2.4
Higher-order
(2
3)
scattering
Now
let us consider
a
NLE
evolution equation:
We assume there exists
a
pseudopotential
u
=
u(x,t)
such that:

414
M.
C.
Nucci
with the integrability condition:
ux
...xt
=
Utx
...x
(n
2
2) (2.40)
-
-
n
n
whenever (2.38)
is
satisfied. Here
R;[u;
z]
(i
=
0,1,.
.
.
,
n)
is
any
element of the Riccati-chain
of
order
n
with respect
to
u
as
a
function
of
x,
i.e.:
and
Fn-2,
. .
.
,
Fo,
F,
Gn-l, . .
.
,
Go,
G
are functions
of
q,
q,,
.
. .
to be
determined by (2.38) and (2.40). If such
a
pseudopotential
u
can be
found, then the Lax equations
(n
+
l-order scattering problem) are
easily obtained from (2.39) by means of the transformation (2.34),
1.e.:
u
=
(log+), (2.42)
where
$
=
+(x,t)
is
the spectral function.
If
we eliminate
q,
q,,
.
.
.
from
(2.39), then the equation satisfied by
u
is obtained.
A
simple
invariance of this equation, e.g.:
u*
=
-u
(2.43)
can generate
an
auteBacklund transformation
of
(2.38)
by eliminat-
ing
u
and
u*
in (2.39) and:
R,[u*;
X]
=
Fn-z(q*,
q:,
-
*
.)Rn-2[~*;
X]
+
* *
*
+
+Fo(q*,
a:,
*
*
.)Rob*;
4
+
+o*,
q;,
* *
.>
(2.44a)

Riccati-type Pseudopotentials
and
Their Applications
415
where
q*
=
q*(z,t)
is another solution of (2.38).
tion:
In the case
of
a
second-order scattering problem, the transforma
(2.45)
applied to the Riccati-type defining equations of the pseudopotentid
u, gives rise to the singularity manifold equation of (2.38), the de-
pendent variable
of
which is
4
=
+(z,t).
This is not true, however,
for
the higher-order members of the Riccati-chain. In some cases,
the singularity manifold equation is derived by the transformation
(2.20) applied to the Lax equations [30].
Applications of this technique can be found in [30].
A
very inter-
esting example
is
given by the
Bullough-Dodd equation:
1
2
=
--(1og4x)z
(2.46)
For
this equation no pseudopotential u exists
so
that the defining
equations are
of
the Riccati-type. However,
a
pseudopotential
u
is
found such that:
%,
=
-311%
-
u3
+
(
-qx,
+
q:)u
+
x
(2.47a)
ut
=
-(ux
+
u2)
+
-
X
x
[",'
e-qqx
.I
(2.47b)
which gives:
e-q
=
ut
+
u Jutdz
(2.48)
>,
ut
=
1
(utu,
+
u3
J
ut dx
-
uuzt
x
where
A
is
a
constant. The Lax equations [14]:
Ilxm
=
(-qzz
+
q:>+z
+
xIl
(2.49)
(2.50a)
(2.50b)

416
M.
C.
Nucci
are easily obtained by applying (2.42) to (2.47).
If
we combine (2.49)
and (2.42), then the equation satisfied by the spectral function
$J
is
given by:
X$$t
+
$ztt$z
-
+zt
(
$tt
+
-
:)=o
(2.51)
It should be remarked that in [15]
a
"generalized pseudopotential"
was
introduced
for
(2.46) which corresponds to the spectral function
$
in our notation.
The equation satisfied by
u
(2.49) is invariant under the trans-
formation:
u*
=
-u,
A*
=
-A
(2.52)
Another solution of (2.46) will correspond to:
UfZ
=
-311-u:
-
u*3
+
(-&
+
q;2)u*
+
A*
(2.53a)
(2.53b)
If
we
combine (2.47a), (2.53a), (2.52) and eliminate
u,
then the fol-
lowing spatial part of an auto-Backlund transformation for (2.46) is
found [16]:
with Q
=
qt,
Q*
=
q;.
The time part is obtained from (2.47b) and
(2.53b) by
a
similar approach. Figure 6 summarizes the properties of
(2.46). Note that neither the equation satisfied by
nor the equation
satisfied by
4,
which is obtained by substituting (2.45) into (2.49),
1.e.:

Riccati-type Pseudopotentials and Their Applications
are invariant under the Mobius group:
417
(2.56)
This is in agreement with
the
results in
[43],
where
it
was shown that
the overdetermined system
of
equations
for
the ”singularity function”
has
only trivial solutions.
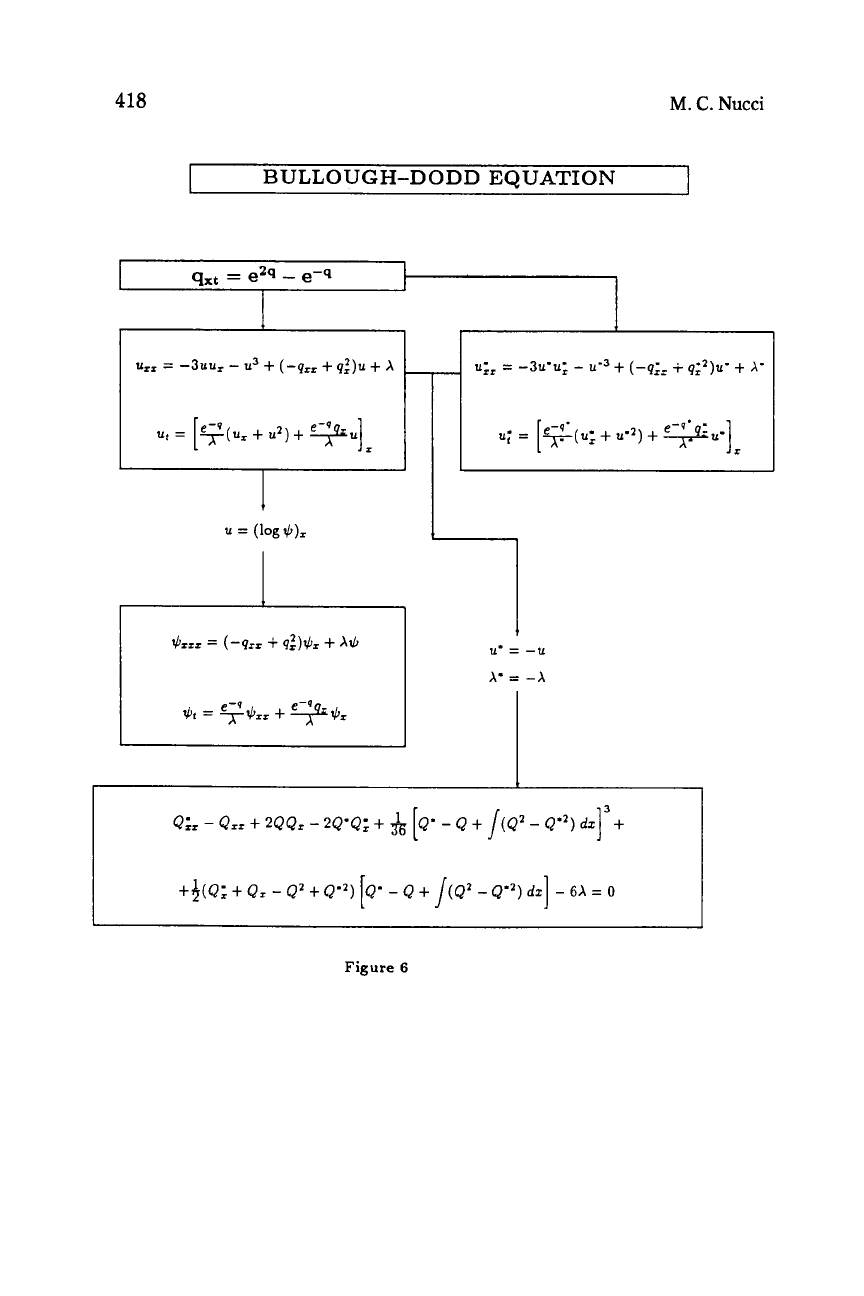
418
M.
C.
Nucci
BULLOUGH-DODD EQUATION
I
u;,
=
-3u-u;
-
u-3
+
(-q;=
-i
q;Z)u-
+
A’
-I
Q;,
-
Q,,
+
2QQ,
-
2Q’Q;
+
&
Q’
-
Q
+
(QZ
-
Q”)
dzI3
+
[J
+$(Q;
+
Q,
-
QZ
+
Q”)
[Q.
-
Q
+
/(Qz
-
Q”)
dz]
-
6X
=
0
Figure
6

Riccati-type Pseudopotentials and Their Applications
419
3
Riccati-type pseudopotentials
for
NLE
equa-
tions in
2+1
dimensions
The
2+1
dimensional case is rather more complicated.
Let us con-
sider nonlinear evolution equations of the form:
9,
qx,
qy,
qxx,
qxY,
J
qy
dx,
-
-
.)
(34
We assume that there exists
a
pseudopotential
u
=
u(t,x,y)
such
that:
(3.2a)
(3.2b)
with the requirement that
uxt
=
utX
whenever
(3.1)
is satisfied. Then
(2.16)
could
be
applied to
(3.2),
which will give the
Lax
equations for
(3.1).
If we can find another pseudopotential
u*
which has
a
simple
transformation to
u,
e.g.:
u*
=
-u
(3.3)
then we can easily obtain an auto-Backlund transformation for
(3.1).
Finally, we get the singularity manifold equation for
(3.1)
from the
Lax equations through
(2.20),
as
in
1+1
dimensions.
It should be
remarked that
(2.22)
does not hold true in
2+1
dimensions, because
the Wronskian of
$1
and
$2
with respect to
x
is never equal to one.
We now apply this technique to the
Kadomtsev-Petviashvili
equation:
qt
=
qxxx
-
6qqx
+
3
J
qyy
dx
(3.4)
