Ames W.F., Roger C. Nonlinear equations in the applied sciences. Volume 185
Подождите немного. Документ загружается.

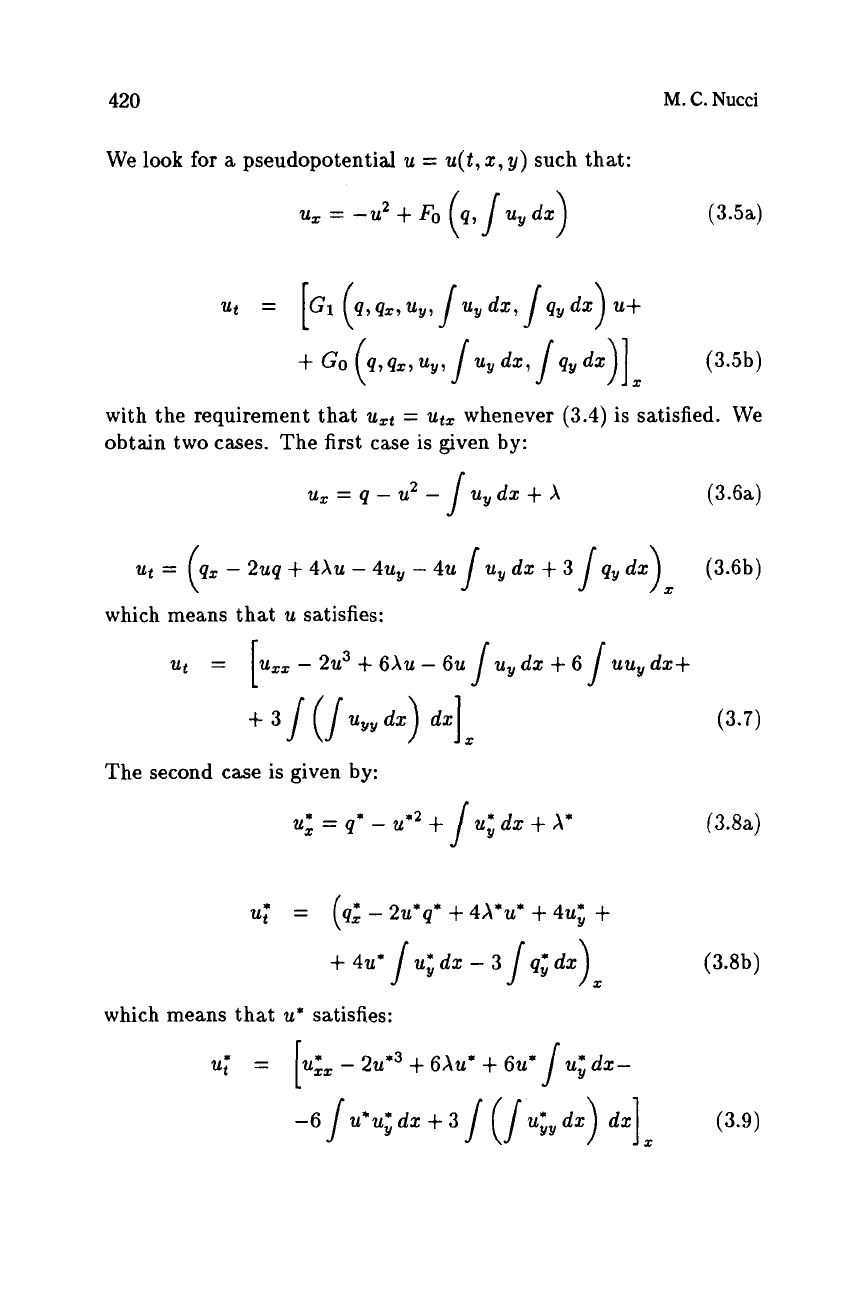
420
M.
C.
Nucci
We
look
for
a
pseudopotential
u
=
u(t,
x,
y)
such that:
U,
=
-u'+
Fo
(3.5a)
+GO
(q,qx,uy, Juydx, JqYdx)]
X
(3.5b)
with the requirement that
uXt
=
utx
whenever
(3.4)
is satisfied. We
obtain two cases. The first case is given by:
U,
=
q
-
u2
-
uydx
+
X
(3.6a)
J
ut
=
qx
-
2uq
+
4~u
-
4uy
-
4u
J
uy dx
+
3
J
qy
dx) (3.6b)
(
X
uXx-2u3+6Au-6u Juydx+6 Juuydx+
which means that
u
satisfies:
The second case is given by:
uj.
=
q*
-
u*'
+
u; dx
t
A*
(3.8a)
J
u;
=
(q:
-
2u*q*
+
4X*u*
+
421;
+
which means that
u*
satisfies:
uZx
-
2u*3
+
6Au*
+
6u*
u;
dx-
J
(3.8b)

Riccati-type Pseudopotentials and
Their
Applications
421
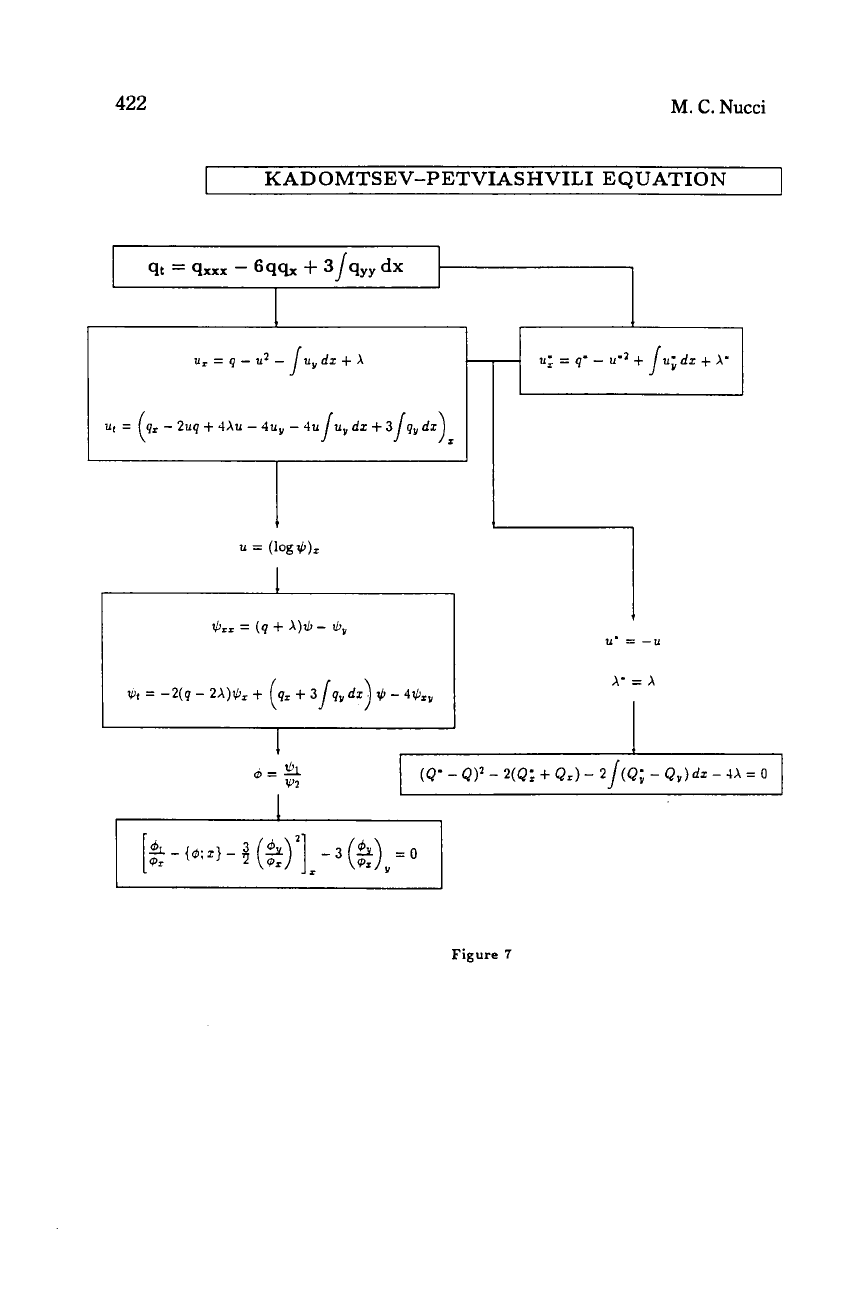
It easy to show that:
Then the
tained
[9]:
(9'
-
u*
=
-u
A*
=
X
(3.10)
following auto-Backlund transformation for (3.4) is ob-
Q)2
-
2(Q:
+
Qx)
-
2 /(Q;
-
Qy)
dx
-
4X
=
0
(3.11)
where Qx
=
q
and QZ
=
q*.
If
we apply:
to (3.6), we obtain the
Lax
equations [20]:
+m
=
(q
+
X)ll,
-
?by
(3.13a)
+t
=
-2(q
-
2Wx
+
(3.13b)
In [24], the differential form approach was used to generate the
Lax
equations for (3.4). If we apply (2.20) to the
Lax
equations, we
obtain the singularity manifold equation
of
(3.4) [42]:
(&).I2
-
3
(2)
=
o
(3.14)
2
42
Y
Figure 7 summarizes these results. Figure
8
gives the
Lax
equations,
auteBacklund transformation and singularity manifold equation of
the Boussinesq equation. This equation is not
a
(2+1)-dimensional
NLE
equation, but it can be derived from the Kadomtsev-Petviashvili
equation if we apply the following transformation on the independent
variables:
t=O
y=r
(3.15)
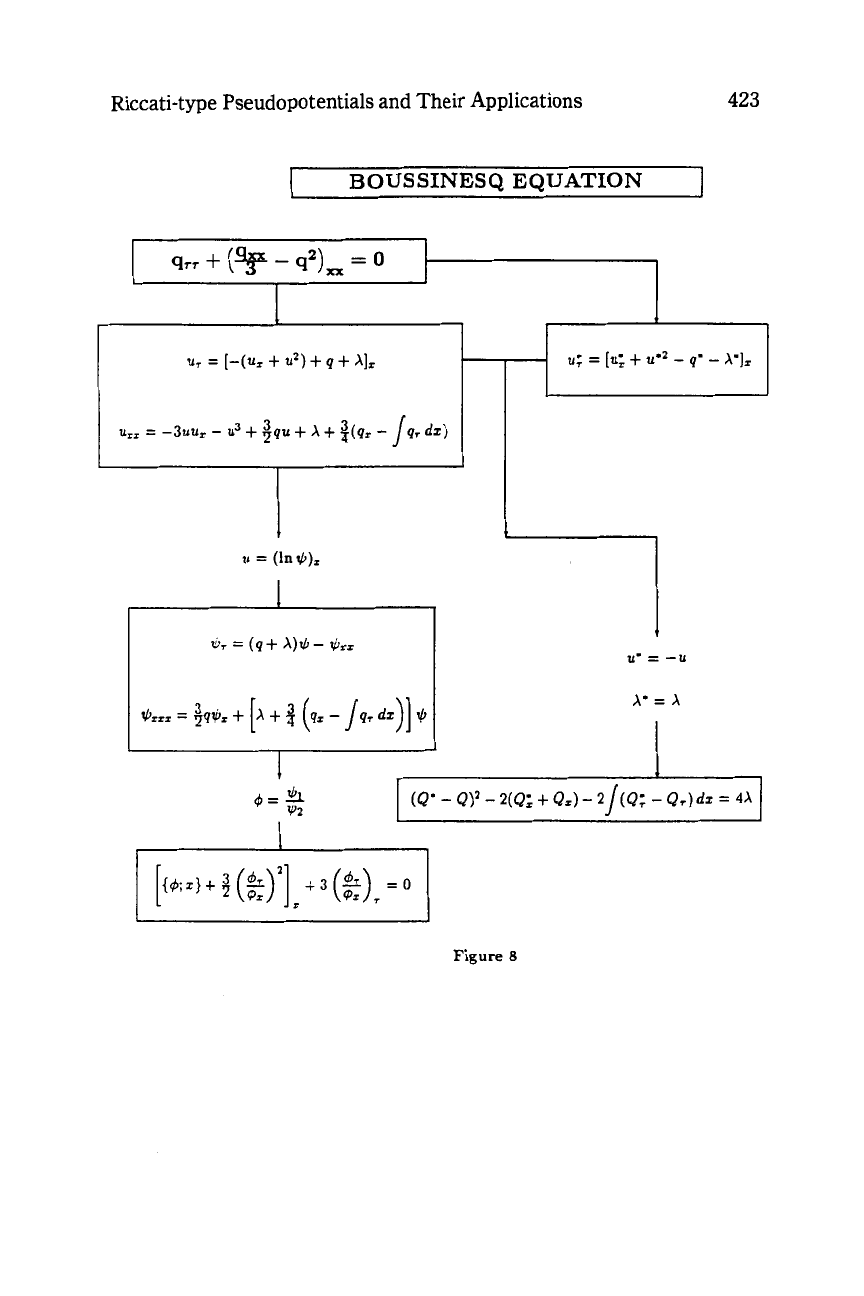
It should be noticed that the Boussinesq equation gives rise
to
a
third-order scattering problem. In fact, the defining equations of its
pseudopotential correspond to
R2
in the Riccati-chain. Furthermore,
the singularity manifold equation can be obtained by (2.20). In [23],
the differential form approach
was
used to generate the
Lax
equations
of
the Boussinesq equation.
Other examples in 2+1 dimensions can be found in [27], [28].
422
b=gl
w2
M.
C.
Nucci
(Q’
-
Q)Z
-
2(Q;
+
Q,)
-
2/(Q;
-
Q.)
dz
-
4A
=
0
KAD OMTS EV-PETVIAS HVILI EQUATION
A’
=
A
Figure
7
Riccati-type Pseudopotentials and Their Applications
423
I
BOUSSINESO
EOUATION
1
u;
=
[u;
+
U.2
-
q'
-
A'],
-I
t
Figure
8

424
M.
C.
Nucci
4
Singularity manifold equations and recip-
rocal aut
o-B
acklund transformat ions
In 1983 the concept of the singularity manifold equation
was
intro-
duced [44].
While it plays
an
important rBle in establishing if
a
partial differential equation possesses the Painlevd property, the sin-
gularity manifold equation did not seem
to
have other applications.
In
an
appendix
to
one of his papers
[38],
Weiss noticed that the sin-
gularity manifold equation of the Korteweg-de Vries equation could
be transformed into the Harry Dym equation via an inverse trans-
formation plus
a
change of dependent variable. In [36], Rogers and
Wong derived
a
reciprocal auto-Backlund transformation [19] for the
Harry Dym equation. All these results were found
to
be true for the
Korteweg-de Vries hierarchy [34]: the Harry Dym hierarchy was ob-
tained by applying
a
reciprocal Backlund transformation [19] to the
equations satisfied by the potentials of the singularity manifold func-
tions. In 2+
1
dimensions, substituting the Kadomtsev-Petviashvili
equation for the Korteweg-de Vries equation, Rogers [32] obtained
the (2+1)-dimensional Harry Dym equation and its auto-Backlund
transformation using the same approach. He noticed that the recip-
rocal
auto-Blklund transformation
was
induced by the invariance
of the singularity manifold equation under the Mobius group.
In
[33],
analogous results were obtained for both the Caudrey-Dodd-
Gibbon and Kaup-Kuperschmidt hierarchies and two different hier-
archies based on Kawamoto-type equations were derived. In [29], it
was shown that these results are not exclusive
to
few cases but they
are generalizable
so
that any singularity manifold equation generates
a
novel equation and its auto-Backlund transformation. Let us
see
how this works. In
1+1
dimensions,
a
singularity manifold equation
in
4(x,t)
is made of combinations of terms such
as:
4t
4X’
-
and their derivatives, which are invariant under the Mobius group:

Riccati-type Pseudopotentials and Their Applications
425
(ad
-
bc
#
0;
a,
b,
c,
d
=
constants).
As
in
[38],
if we apply
an
inverse transformation
[4],
i.e.:
2
+
4,
t
-f
t,
4+x
(4.3)
the following equalities
are
true:
?Tow we have an equation in
x
=
z(4,
t).
If we make the substitution:
x
=
/v-'d4
(4.5)
which implies:
X&
=
-v-2vt,
{x;
4)/x2
=
-vw+~
+
4/2 (4.6)
we obtain
a
novel equation (N.E.) in
v.
Finally, the invariance
of
the
singularity manifold equation under the Mobius group
(4.2)
induces
the following auto-Bkklund transformation:
(ad
-
bc)v
=
(cJv-1
d++d)*
(4.7)
coupled with
(4.2).
with:
In
2+1
dimensions, we use the same procedure, via
(4.3)
coupled
Y-fY
(4.8)
which yields:
X
a,
=
-gad
+
a,
Xb
(4.9)
We
will now consider the singularity manifold equation (S.M.E.) of
the Burgers equation. In
[26],
the
Burgers
equation:
qt
=
qzz
+
qqz
(4.10)

426
M.
C.
Nucci
was shown to possess
a
pseudopotentid
u
=
u(x,
t)
such that3:
qx
tL2
q2
'11=
=
-
+
-
-
-
228
(4.11a)
(4.11b)
In [28], the transformation:
'11
=
(1n4x)x (4.12)
was
used to obtain the singularity manifold equation for (4.10):
(4.13)
xx
If we apply the inverse transformation (4.3) to (4.13), and use (4.4),
we obtain:
Substituting (4.5) and deriving by
4
will give
a
N.E.
in v(4,t):
(4.15)
2VV&
-
2vtv4
-
v3v444
21
v:
vtt
=
2-
+
v2
?I
An auto-Backlund transformation for (4.15) is given by (4.2) and
(4.7), where v*(@,
t)
is another solution of (4.15). Figure 9 summa-
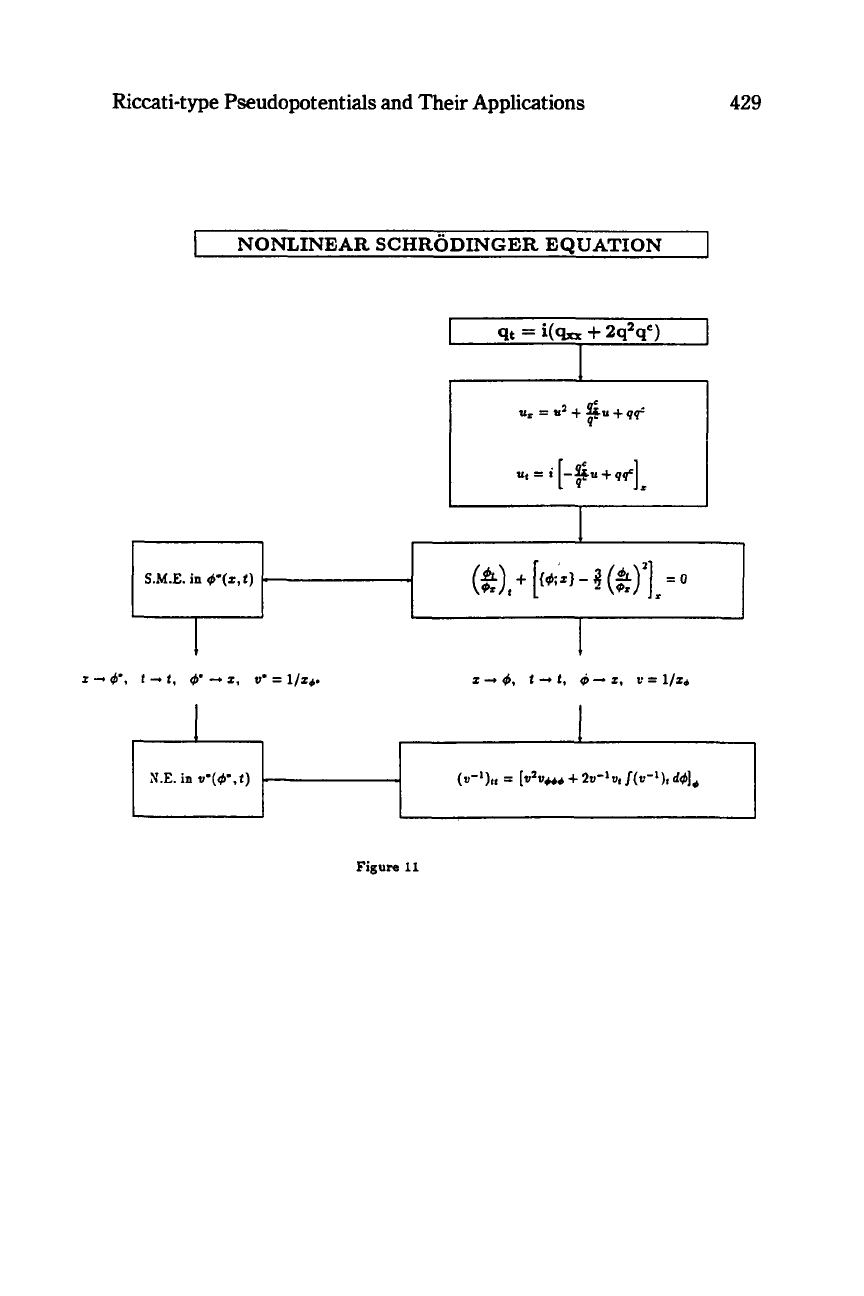
rizes these results for the Burgers equation. Other examples given in
Figures 10 through 12 are the sine-Gordon, nonlinear Schrijdinger,
and
(2+
1)-dimensional Sawada-Kotera equations4, respectively.
More examples can be found in [29].
3We assume
A
=
0
to simplify the calculations.
'Note that the diagram in Figure
12
is not complete, because of the small
space available.

Riccati-type Pseudopotentials and Their Applications
BURGERS EQUATION
427
Figure
9

428
M.
C.
Nucci
I
SINE-GORDON
EQUATION
I
II
I
I
I
Figure
10
Riccati-type Pseudopotentials and Their Applications
X.E.
in
u'(&.t)
429
.
(u-1)ff
=
[U2W*r,
+
2u-'uf
J(o-'),d4],
NONLINEAR SCHRODINGER EQUATION
2
+
4,
1
-
t,
4-
I, o=
112,
