Ames W.F., Roger C. Nonlinear equations in the applied sciences. Volume 185
Подождите немного. Документ загружается.

430
M.
C.
Nucci
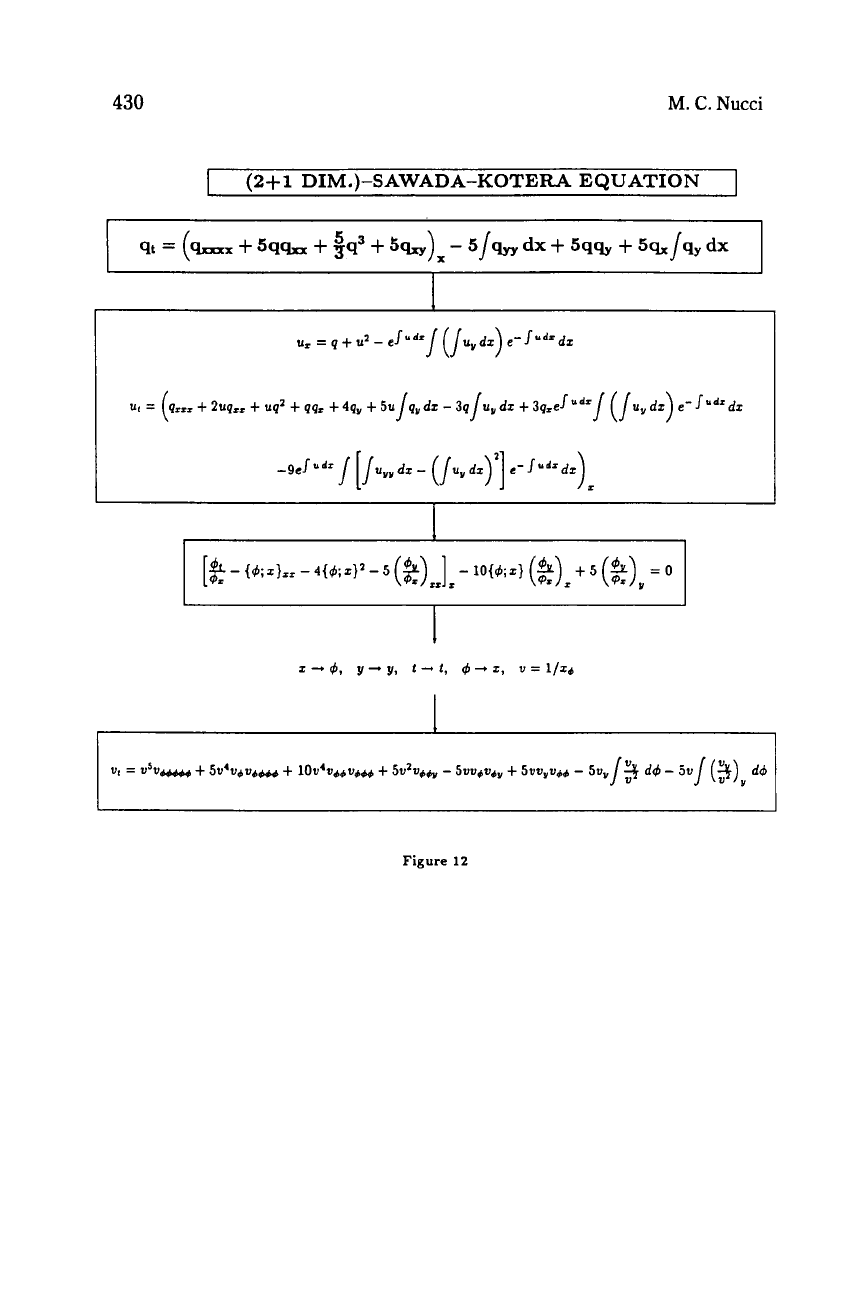
(2+1
DIM.)-SAWADA-KOTERA EQUATION
I
.9elud'/
[/uyydt
-
(/u,dz)']
e'fYdrdz)
r
t
+
4,
y-
y,
c
+
i,
4-
2,
u=
1/24
Figure
12

Riccati-type Pseudopotentials and Their Applications
43
1
5
Riccati-type pseudopotentials and
non-integrability
Riccati-type pseudopotentials always exist
for
any
NLE
equation in
1+ 1
dimensions:
Qt
=
H(q7
qx,
QXX,
Qxtz,
* *
.)
(5.1)
which has local conservation laws of the form:
ft
=
92
(5.2)
where
f
and
g
are functions
of
q
and its derivatives by
5.
If
(5.1) is
not S-integrable, then the only Riccati-type pseudopotentids involve
expressions of the local conservation laws, i.e.5:
fx
ux
=
-u2
+
(7
+
pj
-
277
u
+
Af2
+
77
(5
+
pj
-
7)
(5.3a)
ut=
(yu+q-+v)
9+P
f
X
(5.3b)
where
p,
q,
A,
p,
v
are
arbitrary constants.
If
we apply:
u
=
(log$),
(5.4)
then we obtain the
Lax
equations given in
[8].
Note that for
7
=
0,
these
Lax
equations reduce to:
$xz.
=
($
+
Pf)
$x
+
Xf2$
+t
=
y$x
+
”$
(5.5a)
(5.5b)
which were shown to be trivial in
[8].
As
an example we consider the
Kuramoto-Sivashinsky equation
[
121:
qt
=
(qxxx
+
Qx
+
q2)x
(5.6)
A
pseudopotential
u
given by
(2.15),
i.e.:
Uz
=
-u2
+
F1(q)u
+
Fo(q)
(5.7a)
5We
assume
k
=
-1.

432
M.
C.
Nucci
ut
=
[Gl(q,
qx,
~z)u
+
Go(Q,
qz,
qzx)]z
(5.7b)
does not exist.
If
we look for
a
pseudopotential
u
such that:
ut
=
[Gl(q,
qz,
qzz,
qzzx)~
t
Go(q,
qz,
qzz,
qzzz)Ix
(5.8b)
we find only (5.3) with
f
=
q
+
c1
and
g
=
qxxz
t
qz
+
q2
+
c2
(CI
and
c2
are arbitrary constants). Other examples can be found in
[8].
Bibliography
[l]
M.
J.
Ablowitz, D.
J.
Kaup, A.
C.
Newell and H. Segur, "Non-
linear evolution equations of physical significance", Phys. Rev.
Lett.
31
(1973) 125-127.
[2]
M.
J.
Ablowitz and
H.
Segur,
Solitons and Inverse Scattering
Tmnsform,
SIAM, Philadelphia (1981).
[3] W.F. Ames,
Nonlinear Ordinary Differential Equations in
Tmnsport Processes,
Academic Press, New York (1968).
[4]
W
.F.
Ames,
Nonlinear Partial Differential Equations in Engi-
neering,
Vol.
2,
Academic Press, New York (1972).
[5]
R.L.
Anderson and
N.H.
Ibraghimov,
Lie-Bicklund Transfor-
mation in Applications,
SIAM, Philadelphia (1979).
[6] F. Calogero, "Why are certain nonlinear PDEs both widely ap-
plicable and integrable?", in
What
is
integmbility (for nonlinear
PDEs)?
(ed. V.E. Zakharov) Springer-Verlag, Berlin (1988) to
be published.
[7]
F.
Calogero and A. Degasperis,
Spectml transform and solitons:
tools to solve and investigate nonlinear evolution equations, Vol.
1,
North Holland, Amsterdam (1982).

Riccati-type Pseudopotentials and Their Applications
433
[8]
F.
Calogero and M.C. Nucci,
”Lax
pairs galore”,
J.
Math. Phys.
(1990)
to be published.
[9]
H.-H. Chen, ”A Backlund transformation in two dimensions”,
J.
Math. Phys.
16
(1975) 2382-2383.
[lo]
H.-H. Chen, ”Relation between Backlund transformations and
inverse scattering problems”, in
Biicklund Tmnsformations, the
Inverse Scattering Method, Solitons, and Their Applications
(ed.
R.M. Miura)
(Lecture Notes in Mathematics
515)
Springer-
Verlag, Berlin
(1976) 241-252.
[ll]
P.A. Clarkson, ”The PainlevC conjecture, the PainlevC prop-
erty for partial differential equations and complete integrabil-
ity”, Physica
D
18
(1986) 209-210.
[12]
R. Conte and M. Musette, ”Painlev6 analysis and Backlund
transformation in the Kuramoto-Sivashinsky equation”, J. Phys.
A:
Math. Gen.
22
(1989) 169-177.
(131
J.P.
Corones and
F.J.
Testa, ”Pseudopotentials and their Ap-
plications”, in
Biicklund Transformations, the Inverse Scatter-
ing Method, Solitons, and Their Applications
(ed. R.M. Miura)
(Lecture Notes in Mathematics
515)
Springer-Verlag, Berlin
(1976) 184-198.
[14]
P.
Fordy and
J.
Gibbons, ”Integrable nonlinear Klein-Gordon
equations and Toda lattices”, Commun. Math. Phys.
77
(1980)
2 1-30.
[15]
B.
Gaffet,
”A
class of
l-D
gas
flows
soluble by the inverse scat-
tering transform”, Physica
D
26
(1987) 123-139.
[16]
B. Gaffet, ”Common structure of several completely integrable
non-linear equations”,
J.
Phys. A: Math. Gen.
21
(1988) 2491-
2531.
[17]
A.C. Hearn,
REDUCE
User’s Manual. Version
3.3,
The Rand
Corporation, Santa Monica
(1987).

434
M.
C.
Nucci
[18]
E. Hille,
Ordinary Differential Equations in the
Complex
Do-
main,
Wiley
&
Sons,
New
York
(1976).
I191
J.G. Kingston and C. Rogers, "Reciprocal Backlund transforma-
tions of conservation laws", Phys. Lett. A
92
(1982) 261-264.
[20]
B.G. Konopelchenko and V.G. Dubrovsky, "Some new inte-
grable nonlinear evolution equations in
2
+
1
dimensions", Phys.
Lett. A
102
(1984) 15-17.
[21]
P.
D.
Lax,
"Integrals of nonlinear equations
of
evolution and
solitary waves", Comm. Pure Appl. Math.
21
(1968) 467490.
[22]
R. M. Miura, "The Korteweg-de Vries equation:
a
survey of
results", SIAM Rev.
18
(1976) 412-459.
[23]
H.C. Morris, "Prolongation structures and
a
generalized inverse
scattering problem",
J.
Math. Phys.
17
(1976) 1867-1869.
[24]
H.C. Morris, "Prolongation structures and nonlinear evolution
equations in two spatial dimensions",
J.
Math. Phys.
17
(1976)
1870-1872.
[25]
M.C. Nucci, "Pseudopotentials,
Lax
equations and Backlund
transformations for non-linear evolution equations",
J.
Phys. A:
Math. Gen.
21
(1988) 73-79.
[26]
M.C. Nucci, "Pseudopotentials and integrability properties of
the Burgers' equation", Atti Sem. Mat. Fis. Univ. Modena
38
(1990) 313-317.
[27]
M.C. Nucci, "Pseudopotentials for non-linear evolution equa,
tions in
2
+
1
dimensions", Int.
J.
Non-Linear Mech.
23
(1988)
361-367.
[28]
M.C. Nucci, "Painlev4 property and pseudopotentials for non-
linear evolution equations
",
J. Phys. A: Math. Gen. 22
(1989)
2897-29 13.

Riccati-type Pseudopotentials and Their Applications
435
[29]
M.C. Nucci, "Reciprocal auto-Backlund transformations via the
Mobius group", Atti Sem. Mat. Fis. Univ. Modena
(1990)
to be
published.
[30]
M.C. Nucci, "Riccati-chain type pseudopotentials, higher-order
scattering and Backlund transformations
for
non-linear evolu-
tion equations", Preprint GT
Math:052190-040 (1990).
[31]
M.
Omote, "Prolongation structures of nonlinear equations and
infinite-dimensional algebras",
J.
Math. Phys.
27
(1986) 2853-
2860.
[32]
C. Rogers, "The Harry-Dym equation in
2+1
dimensions:
a
re-
ciprocal link with the Kadomtsev- Petviashvili equation", P hys.
Lett.
A
120
(1987) 15-18.
[33]
C. Rogers and
S.
Carillo, "On reciprocal' properties of the
Caudrey- Dodd- Gibbon and Kaup-Kupershmid t hierarchies",
Physica Scripta
36
(1987) 865-869.
[34]
C. Rogers and M.C. Nucci, "On reciprocal auto-Backlund
transformations and the Korteweg-de Vries hierarchy", Physica
Scripta
33
(1986) 289-292.
[35)
C. Rogers and W.F. Shadwick,
Ba'ckfund
Tmnsform~tions
and
Their
Applic~tions,
Academic Press, New York
(1982).
[36]
C. Rogers and P. Wong, "On reciprocal Backlund transforma-
tions
of
inverse scattering schemes", Physica Scripta
30
(1984)
10-13.
[37]
H.D. Wahlquist and F.B. Estabrook, "Prolongation structures
of nonlinear evolution equations",
J.
Math. Phys.
16
(1975) 1-7.
[38]
J.
Weiss, "The PainlevC property for partial differential
equations.
11:
Backlund transformations,
Lax
pairs, and the
Schwarzian derivative",
J.
Math. Phys.
24
(1983) 1405-1413.
[39]
J.
Weiss, "On classes of integrable systems and the PainlevC
property",
J.
Math. Phys.
25
(1984) 13-24.

436
M.
C.
Nucci
[40]
J.
Weiss, ”The sine-Gordon equations: Complete and partial
integrability”,
J.
Math. Phys.
25
(1984) 2226-2235.
[41]
J.
Weiss, ”The Painlev6 property and Backlund transformations
for the sequence
of
Boussinesq equations”,
J.
Math. Phys.
26
(1985) 258-269.
[42]
J.
Weiss, ”Modified equations, rational solutions, and the
Painlev6 property for the Kadoxntsev-Petviashvili and Hirota-
Satsuma equations”,
J.
Math. Phys.
26
(1985) 2174-2180.
[43]
J.
Weiss, ”Backlund transformation and the Painlev6 property”,
J.
Math. Phys.
27
(1986) 1293-1305.
[44]
J.
Weiss, M. Tabor and
G.
Canevale, ”The Painlev6 property
for partial differential equations”
J.
Math. Phys.
24
(1983) 522-
526.

Nonlinear Elasticity
:
Incremental Equations
and
Bifurcation Phenomena
R.
W.
Ogden
University
of
Glasgow
Abstract
This paper begins with
a
summary
of
the basic equations govern-
ing nonlinear quasi-static deformations of an elastic solid. Attention
is then focussed on the linearized equations associated with incremen-
tal deformations superimposed
OR
an underlying finite deformation.
The question
of
stability of the underlying deformation is then exam-
ined and the connection between stability and uniqueness of solution
of incremental boundary-value problems discussed. Non-uniqueness
of
solution is illustrated in two simple examples-bifurcation from
a
homogeneously deformed configuration under dead loading, and
surface deformations on
a
pre-stressed half-space.
1
Introduction
The mathematical theory of elasticity has
a
long history and has
its roots in engineering mechanics;
in
particular, the linear theory
has
been developed over
a
period of more than 300 years.
As
well
as
providing many challenges for mathematicians, the linear theory has,
within certain limitations, satisfied the needs of applications in, for
example, structural mechanics, fracture mechanics and seismology.
The linear theory remains
a
very active area of research and still
offers
a
wide range of opportunities for mathematical development.
It is only relatively recently that the
nonlinear theory of elasticity
has received comparable attention; the theory has developed rapidly
Nonlinear
Equations
in
the Applied Sciences
437
Copyright
0
1992
by
Academic Press,
Inc.
All
rights
of
reproduction
in
any
form
reserved.
ISBN
0-12-056752-0

438
R.
W.
Ogden
since the
1940’s,
stimulated by the need to describe and explain the
mechanical behaviour
of
materials, such
as
natural rubber, which are
capable of undergoing large elastic deformations. The fabrication
of
synthetic rubber-like materials has provided further stimulus, and,
more recently, application
of
the theory to the study of the mechanics
of
biological tissues has been much in evidence. The range of appli-
cations is growing, a.nd nonlinear elasticity can now be regarded
as
very much an interdisciplinary subject area, impinging on engineer-
ing, materials science, chemistry, physics and biology. The inherent
nonlinearity of the mathematical theory presents many difficulties
but it also offers
a
wealth
of
exciting and challenging opportunities
for researchers in
a
diversity
of
fields, but notably in theoretical me-
chanics, applied mathematics, pure mathematics, numerical analysis
and computational mechanics.
In
this article the intention is not to provide
a
comprehensive
account
of
nonlinear elasticity but to concentrate
on
the main in-
gredients of the theory and to illustrate how the nonlinearity influ-
ences the nature
of
the solution of some very simple boundary-value
problems. Different flavours
of
the theory, with varying degrees of
mathematical sophistication, are encountered
in
the literature, and
the reader is referred to the texts by Truesdell and No11
[20],
Marsden
a.nd Hughes
[ll],
Ogden
[14]
and Ciarlet
[GI,
in particular, for more
details
of
the theory. Only
a
limited number of selected papers are
cited here and in general, rather than give full documentation, we
point to the above-mentioned monographs for references to original
sources; see also the recent review article by Beatty
[4].
2
Basic Equations
2.1
Kinematics
We consider
a
continuous body which occupies
a
connected open
subset of
a
three-dimensional Euclidean point space, and we refer to
such
a
subset
as
a
configuration
of
the body. We identify an arbitrary
configuration as
a
reference configuration
and denote this by
B,.
Let
points in
B,
be labelled by their position vectors
X
relative
to
an

Nonlinear Elasticity
439
arbitrarily chosen origin and let
dB,.
denote the boundary off?,. Now
suppose that the body is deformed quasi-statically froin
B,
so
that it
occupies
a
new configuration,
B
say, with boundary
Of?
-
we refer to
B
as
the
current configuration
of the body. The deformation can be
represented by the ma.pping
x:
B,
-+
B
which takes points
X
E
B,
to points
x
E
B
according to
x=x(X)
XEB,,
(1)
where
x
is the position vector of the point
X
in
B.
The mapping
x
is
called the
deformation
from
B,
to
0.
We require
x
to be one-to-one
and, for purposes
of
this article, twice continuously differentiable.
For simplicity, we consider only Cartesian coordinate systems
and let
X
and
x
respectively have coordinates
X,
and
x;,
where
a,
i
E
{1,2,3},
so
that
x;
=
XI(&).
Greek and Roman indices refer
respectively to
B,
and
B,
and the usual summation convention will
be used.
The
deformation gradient tensor
A
is given by
A
=
Gradx
(2)
and has Cartesian componeiits
A;,
=
dxi/aX,,
Grad being the gra-
dient operator in
B,.
Local invertibility of
x
requires that
A
is non-
singular, and we adopt the usual convention det
A
>
0
and the nota-
tion
J
=
det
A.
(3)
Locally,
A
describes the deformation in the neighbourhood of the
point
X.
The
polar
decompositions
A
=
RU
=
VR,
where
R
is proper orthogonal and
U, V
are positive definite and sym-
metric, are unique.
Respectively,
U
and
V
are called the
right
and
left stretch tensors.
(4)
We also have the
spectral decomposition
i=l
