Astakhov V. Tribology of Metal Cutting

Подождите немного. Документ загружается.

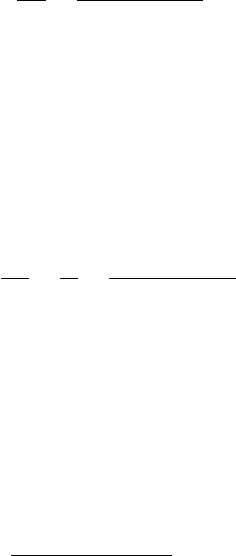
Cutting Tool Wear, Tool Life and Cutting Tool Physical Resource 227

As it follows from Eq. (4.3), the dimension wear rate is inversely proportional to tool

life but it does not depend on the selected wear criterion (a particular width of the ﬂank

wear land, for example).

• The surface wear rate is the radial wear per 1000 sm

of the machined area (S)

(

−h

r−i

)

100

(

l − l

)



µm/10



, (4.4)

where h

r−i

and l

are the initial radial wear and initial length of the tool path,

respectively and l is the total length of the tool path.

As it follows from Eq (4.4), the surface wear rate is reverse proportional to the overall

machined area and, in contrast to it, does not depend on the selected wear criterion.

• The speciﬁc dimension tool life is the area of the workpiece machined by the tool

per 1 µm of its radial wear

(

l − l

)

(

−h

r−i

)

100



/µm



. (4.5)

The surface wear rate and the speciﬁc dimension tool life are versatile tool wear charac-

teristics because they allow to compare different tool materials for different combinations

of the cutting speeds and feeds using different criteria selected for assessment of tool

life. Table 4.2 presents a comparison of different assessments of tool wear and thus the

tool life.

It is possible to use the width of the wear land at the tool point (nose) (current VB

and

initial VB

C−i

) instead of the radial wear (Fig. 4.1) to calculate the surface wear rate, i.e.

(

−VB

C−i

)

100

(

l − l

)



µm/10



. (4.6)

Although such a substitution is correct, it is difﬁcult to correlate VB

with the dimensional

accuracy of machining. This is due to the plastic lowering of the cutting edge, which

often occurs in machining difﬁcult-to-machine materials.

4.4 Optimal Cutting Temperature – The First Metal Cutting Law

4.4.1 The essence of the ﬁrst metal cutting law (the Makarow’s law)

As discussed in Chapter 3, the cutting temperature is understood as the mean integral

temperature at the tool–chip and tool–workpiece interfaces as measured by a tool-work

thermocouple. As conclusively proven by Makarow [14], this temperature is the most

suitable parameter to correlate the tribological conditions at the discussed interfaces with

tool wear. Therefore, the correlation of this temperature with parameters of the cutting

system should be established.

228 Tribology of Metal Cutting

Table 4.2. Comparison of different characterizations of tool life.

Characteristic Designation/equation Restriction factors

Possibility to use in calcula-

tions of dimension accuracy

Cutting speed (ν (m/min))

Cutting feed (f (mm/rev))

Dimensions of the

machined part (surface)

Tool wear VB

or VB

Machining time without

adjustment or

replacement of the tool

(min)

c−l

++− +No

Number of part produced

without adjustment or

replacement of the tool

p−l

−−+ +No

Length of the tool path L

c−l

= νT

c−l

−+− +No

Area of the machined

surface

c−l

= 10νT

c−l

f −−− +No

Volumetric or mass tool

wear

−−− −No

Linear relative wear h

l−r

(

−h

r−i

)

1000

(

l−l

)

−+− −Yes

Dimension wear rate ν

νh

l−r

1000

++− −Yes

Surface wear rate h

(

−h

r−i

)

100

(

l−l

)

−−− −Yes

Speciﬁc dimensional tool

life

(

l−l

)

(

−h

r−i

)

100

−−− −Yes

Note that “+” means that the restrictive factors should be kept the same when using this characteristic for

the comparison of cutting tools and regimes.

To do that, a simple factorial design of experiment (DOE) (discussed in detail in

Chapter 5) can be employed. As the result of DOE, the following equation to corre-

late the cutting temperature, θ

with parameters of the cutting regime for a given work

material is obtained

= C

, (4.7)

where C

is constant that depends on the properties of the work material, n

, n

and n

are powers to be determined in DOE (Chapter 5).

Table 4.3 shows the constants and powers obtained in machining different steels. As

shown, the strongest inﬂuence on the cutting temperature has the cutting speed. Makarow

showed [14] that the tougher the work materials (in terms of its machinability) gets,

the stronger the inﬂuence of the cutting speed (compared to other machining param-

eters) becomes. Another important conclusion follows from the analysis of Eq. (4.7)

Cutting Tool Wear, Tool Life and Cutting Tool Physical Resource 229

Table 4.3. Coefﬁcients and powers in Eq. (4.7). Tool material –

P20, rake angle γ = 8

◦

, ﬂank angles of the major and minor

cutting edges, α = α

= 15

◦

, tool cutting edge angle κ

= 45

◦

tool cutting edge angle of the minor cutting edge κ

= 15

◦

Work material C

AISI 1010 228 0.25 0.07 0.03

AISI 1020 269 0.27 0.15 0.10

AISI 1045 352 0.22 0.08 0.05

AISI 1080 224 0.33 0.11 0.07

AISI 07 326 0.28 0.12 0.07

and Table 4.3, namely that the same cutting temperature can be achieved using different

combinations of the terms of Eq. (4.7).

Analyzing a great body of experimental data, Makarow formulated the law [14] which

was presented as the First Metal Cutting Law (the Makarow’s law) by Astakhov [16,17]:

For given combination of the tool and work materials, there is the cutting temperature,

referred to as the optimal cutting temperature θ

opt

, at which the combination of minimum

tool wear rate, minimum stabilized cutting force, and highest quality of the machined

surface is achieved. This temperature is invariant to the way it has been achieved (whether

the workpiece was cooled, pre-heated etc.).

The ﬁrst metal cutting law, established initially for longitudinal turning of various work

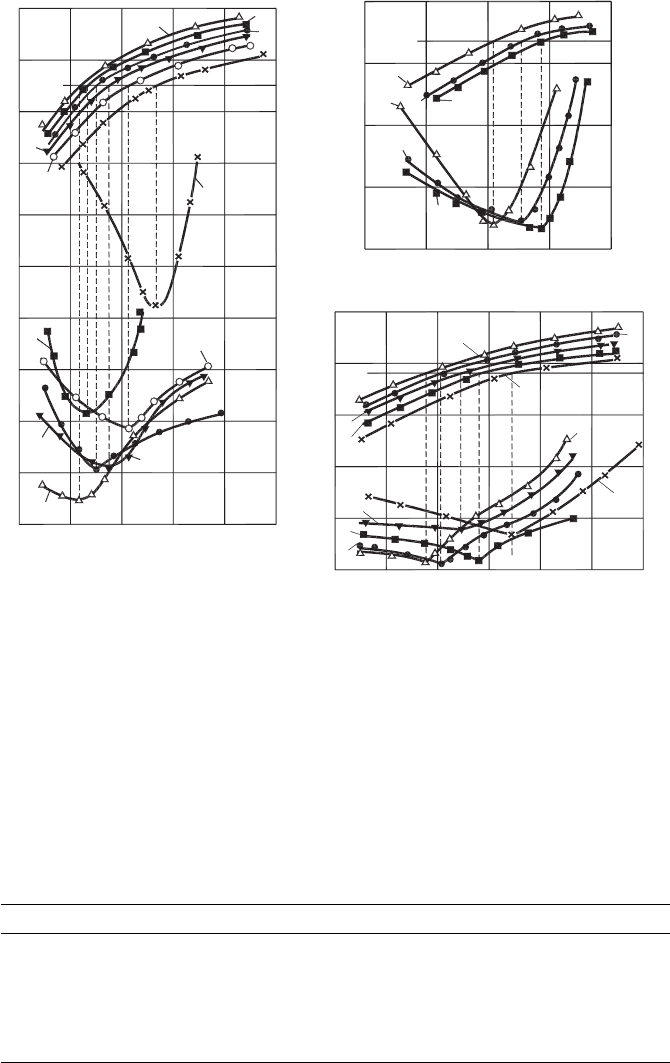
materials (example is shown in Fig. 4.5(a), was then experimentally proven for various

machining operations. Figure 4.5(b) shows its applicability in twist drilling, Fig. 4.5(c) –

in thread cutting, Fig. 4.5(d) – in gear hobbing. Considering Fig. 4.5(a), one can see

that when the cutting feed increases, the surface wear rate reduces. However, minimum

tool wear rates, when various cutting feed are used, occur at the same optimal cutting

temperature θ

opt

, although the amount of the surface wear rate varies more than 2 times.

Even more pronounced effect can be observed in Fig. 4.5(b), where the cutting feed has

a much stronger inﬂuence on tool life, represented by the total length of the tool path to

achieve VB

= 0.3 mm. As shown, there is a speciﬁc combination of the cutting speed

and feed at which tool life is at a maximum. Changing the cutting speed and/or feed on

either side reduces tool life while the minimum tool wear rate under a given combination

of these parameters corresponds to the optimal cutting temperature. Figure 4.5(c) shows

that tool life in thread cutting, represented by the total length of the tool path (L (m)) to

achieve VB

= 0.5 mm, has its maximum at the same optimal cutting temperature, θ

opt

under different combinations of cutting speed and feeds. Figure 4.5(d) shows that the

same conclusion can be drawn from the data for gear hobbing.

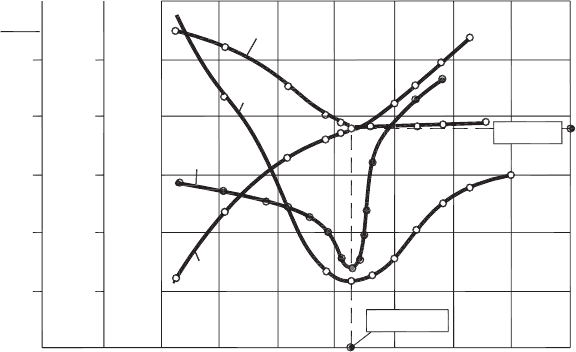
Figure 4.6 shows that the machining at optimal cutting temperature results not only

at the minimum tool wear rate but also leads to obtaining the minimum cutting force

and smallest roughness of the machined surface. As it follows from this picture, under

230 Tribology of Metal Cutting

400

16080 120

(µm/10

)

1200

800

400

300

500

700

160

120

12816

L (mm)

L (m)

100

11070 90

q(°C) q(°C)

q(°C)

opt

q(°C)

800

700

600

N (pc)

400

300

200

(a) (b)

150

200

250

10 20 30

n (m/min) n (m/min)

Fig. 4.5. Optimal cutting temperature: (a) turning, tool material – P30, work material – AISI 1045,

depth of cut d

= 1.5 mm using different cutting feeds: 1 – 1.4, 2 – 0.87, 3 – 0.61, 4 – 0.39 and

5 – 0.39 mm/rev, (b) drilling with twist drills, tool material – HSS T15, work material – AL 610

alloy, drill diameter – 15 mm, tool life criterion – VB

= 0.3 mm using different feeds: 1 – 0.28,

2 – 0.17 and 3 – 0.10 mm/rev, (c) thread cutting with a single-point cutting tool, tool material –

M10, work material – AISI 303, tool life criterion – VB

= 0.5 mm, using different feeds: 1 – 1.0,

2 – 1.5 and 3 – 2.0 mm/rev, (d) gear hobbing, tool material – HSS T15, work material – AISI

4140, module, m = 2 mm, number of teeth z = 61, VB

= 0.7 mm, using different axial feeds:

1 – 4.0, 2 – 2.5 and 3 – 1.7 mm/rev.

given cutting conditions, the optimal cutting temperature θ

opt

= 875

◦

C can be directly

correlated to the so-called optimal cutting speed ν

opt

= 1.28 m/s.

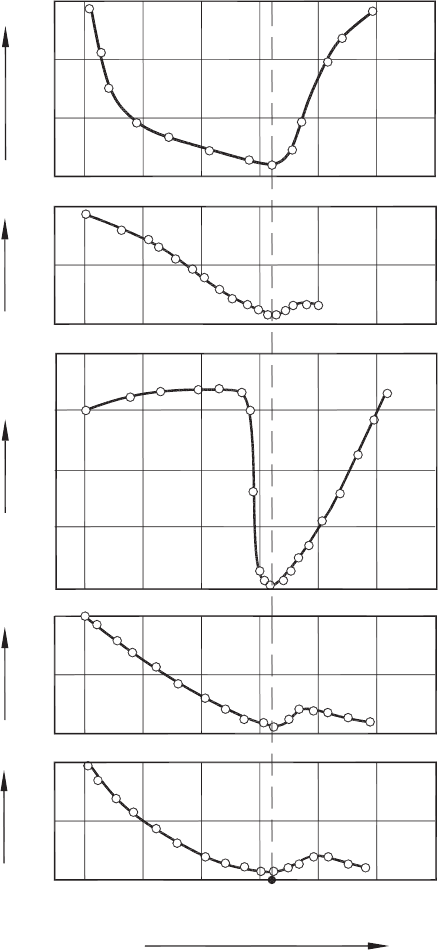
To understand the technical and physical background of the optimal cutting tempera-

ture, one should understand what happens with the work material at this temperature.

Figure 4.7 presents the answers to this question at the technical level. This ﬁgure shows

what happens with the most relevant (to machining) mechanical characteristics of the

work material when this material is brought to the temperature equal to the optimal

Cutting Tool Wear, Tool Life and Cutting Tool Physical Resource 231

0 n (m/s)0.4 0.8 1.2 1.6 2.0 2.4

200

500

700

900

1100

300

400

500

600

700

172

µm

0.1m

θ(°C)

opt

= 1.28m/s

opt

= 875°C

Fig. 4.6. Experimental determination of the optimum cutting speed and temperature using longi-

tudinal turning of AISI 4340 steel. Tool material: carbide P20. Cutting regime: f = 0.15 mm/rev,

=1 mm.

cutting temperature. Particularly, the minima of the ultimate strength, σ

UTS

and elon-

gation, e

(which represents the strain at fracture) result in the minimum work done

in the fracture of the layer being removed as discussed in Chapter 2. The minimum

microhardness, HV assures the minimum of the normal stress at the tool–chip interface

as discussed in Chapter 3. The minimum Young’s modulus assures the minimum work

of elastic deformation (Chapter 2) while the minimum of h

r−s

results in minimum tool

ﬂank wear.

To understand the discussed phenomena at the level of physical metallurgy, one should

recognize that metal cutting is the purposeful fracture of the work material as deﬁned

by Astakhov [16]. As discussed in Chapter 2, the work spent in purposeful fracturing of

the layer being removed, i.e. its fracture toughness, should be considered as the prime

parameter in determining the cutting force and the energy spent in machining. Therefore,

one should consider the mechanics of fracture [18] and the importance of the process

temperature in this mechanics. Another important aspect of metal cutting, discussed in

Chapter 2, is plastic deformation that should be considered as a waste of energy. In metal

cutting, it is desired that the work materials have as small a strain at fracture as possible.

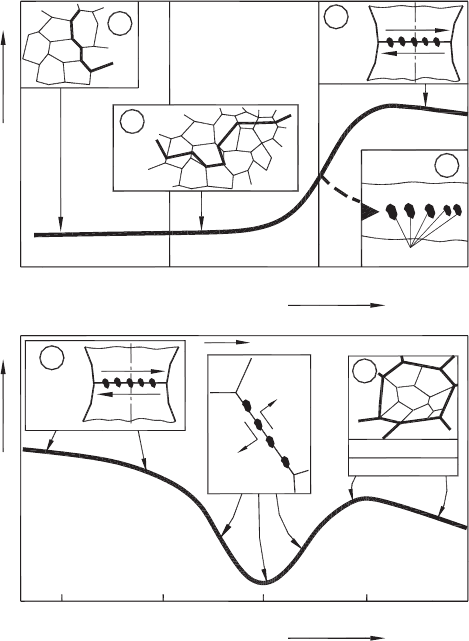
According to Atkins and Mai [18] and Komarovsky and Astakhov [19], there is a marked

increase in the strain at fracture and also in the work of fracture, at about 0.18–0.25 of

the melting point (T

); similar changes occur in other measurements of ductility such

as Charpy values (CVN), as shown in Fig. 4.8(a). It explains a number of “strange”

results obtained by Zorev in his tests at low cutting speeds [20]. This phenomenon also

explains the great size of the zone of plastic deformation observed at low cutting speeds,

and incorporated in the model discussed by Astakhov [16]. The known built-up edge

232 Tribology of Metal Cutting

600 800 1000 1200

150

250

350

uts

(MPa)

100

140

180

HV (MPa)

E (GPa)

100

140

180

(µm/km)

opt

Temperature (°C)

(%)

Fig. 4.7. Inﬂuence of temperature on the properties of pure iron.

Cutting Tool Wear, Tool Life and Cutting Tool Physical Resource 233

voids particles

notch

0.1 0.2 0.30

(0°K)

Ductility

Temperature, T/Tm

Ductility

Room Temp

0.4 0.5 0.60.3

Sliding

Cavities

Recrystallisation

Partial

Full

(a)

(b)

Voids

DIFFUSION IMPORTANT

Fig. 4.8. Changes in ductility and typical associated mechanisms of fracture for bss materials:

(a) at temperatures <0.3 T

: (A) low-temperature intergranular cracks, (B) twinning or slip leading

to cleavage, (C) shear fracture at particles, (D) low energy shear at particles; (b) at temperatures

>0.3 T

: (C) shear at particles, (D) cavities along grain faces, (E) recrystallization suppresses

cavitation.

is the result of the discussed high plasticity region in front of the tool rake face within

the contact length. Exceptions are certain fcc metals and alloys (Al, Cu, Ni, Pb) that do

not normally cleave. As such, there is no transition in values, which gradually rises with

temperature.

The increase in ductility over the “transition temperature range” is followed by a gradual

drop beyond approximately 0.35 T

. It is believed that it happens due to the contin-

uous fall in the Peierls–Nabarro stress which opposes dislocation movement, coupled

with the emergence of cross-slip (as opposed to Frank–Read sources) as a dislocation

generator as the temperature is raised [18]. In the author’s opinion the cause is in

dilation–compression reactions as explained in Ref. [19].

234 Tribology of Metal Cutting

At high temperatures, grain boundaries become signiﬁcant. Below approximately 0.45 T

grain boundaries act principally as barriers inhibiting cleavage and causing dislocation

pile-ups. At higher temperatures, the regions of intense deformation, which are contained

within the grains at lower temperatures, now shift to the grain boundaries themselves.

Voids are nucleated and then cracks develop on the grain boundaries. Shear stresses on

the boundaries cause relative sliding of the grains, and voids are reduced in the region

of stress concentrations (see Fig. 4.8(b) – position D). Therefore, the region around this

temperature can be termed as the ductility valley. Experiments showed [14] that the

reduction of plasticity may reach two fold and even more for high alloys. The presence

of this valley is the physical cause of the existence of the optimal cutting temperature.

At temperatures

(

0.5–0.6

)

, recovery and re-crystallization processes set in (recov-

ery relates to a re-distribution of dislocation sources so that dislocation movement

is easier, and in re-crystallization, the energy of dislocations generated during prior

deformation is used to nucleate and grow new grains, thus effecting annealed struc-

ture over a long time). The net effect is increased ductility causing a bump shown in

Fig. 4.8(b).

4.4.2 Major consequences of the ﬁrst metal cutting law (Makarow’s law)

The following consequences of the ﬁrst metal cutting law are of great importance in the

tribology of metal cutting.

Consequence 1: For cutting tools with various combinations of cutting geometry param-

eters (Appendix A) – rake, ﬂank, inclination, tool cutting edge angles, nose and cutting

edge radii, etc. – the optimal cutting temperature corresponds to the points of minimum

on the curves representing the dependence of tool wear rate on the cutting speed while

the optimal cutting speed corresponding to each and every particular case varies in a

wide range. Figure 4.9(a) and Table 4.4 show an example of experimental veriﬁcation

of this consequence.

Consequence 2: The minimum tool wear rate is achieved at the same optimal temperature

in dry cutting and in cutting with various cutting ﬂuids (media) using various methods of

cutting ﬂuid supply. Figure 4.9(b) demonstrates an example of the obtained experimental

data. As shown, the optimal temperature is the same for dry machining as well as for

machining using different cutting ﬂuids.

Consequence 3: The optimal cutting temperature is the same for various combinations of

the temperature of the preheated workpiece and uncut chip thicknesses. This is illustrated

by an example shown in Fig. 4.9(c) and Table 4.5. In other words, the optimal cutting

temperature does not depend on or is invariant to a particular method by which it was

achieved.

Consequence 4: Variation of the workpiece diameter in turning and boring leads to a

signiﬁcant change in the optimal cutting speed (i.e. the cutting speed corresponding to

the minimum tool wear rate). The reason for this is discussed in Chapter 2, where

the interactions of the deformation and thermal waves are considered. The optimal

Cutting Tool Wear, Tool Life and Cutting Tool Physical Resource 235

0 40 80 120

400

600

200

800

600

400

800

200

400

1000

n (m/min)

6040020

400

800

1200

302010

200

600

400

800

(a)

(b)

(c)

(µm/10

)

(µm/10

)

(µm/10

)

q(°C)

opt

Fig. 4.9. Inﬂuence of cutting speed on the cutting temperature and tool wear rate: (a) wear in

turning AL 610 alloy, tool material – carbide P10 (14% TiC, 8% Co), combinations of the tool

geometry parameters are shown in Table 4.4, (b) wear in turning Haynes 263 alloy (29% Cr,

2.5% Ti), tool material – carbide M20 (92% WC, 8% Co), depth of cut d

= 0.5 mm, cutting

feed f = 0.08 mm/rev, curves: (1) dry cutting, (2) water-based (6%) cutting ﬂuid, (3) oil-based

cutting ﬂuid with chlorine and sulfur, (c) wear in turning Haynes 263 alloy with pre-heating of the

workpiece, tool material – carbide M10 (92% WC, 8% Co), depth of cut d

= 0.5 mm, feeds and

pre-heating temperatures are shown in Table 4.5.

Table 4.4. Regime and geometry parameters in Fig. 4.9(a).

Curve No. d

(

)

(

mm/rev

)

(

◦

)

(

◦

)

(

◦

)

(

◦

)

(

)

1 0.5 10

45 −10 0.3

90 0.1

3 0.09

1.0

4 0.25 0

0.1

530

6 0.18 10 10 1.0

236 Tribology of Metal Cutting

Table 4.5. Parameters of curves in Fig. 4.9(c).

Curve No. f

(

mm/rev

)

(

◦

)

10.11 20

20.21 100

30.3 200

40.11 300

50.3 300

temperature, however, remains the same. This is illustrated by an example shown in

Fig. 4.10.

Consequence 5: If the structure and/or hardness of the work material are changed, the

optimal cutting speed is changed correspondingly, but the optimal temperature, remains

the same. This is illustrated by an example shown in Figs. 4.11(a) and (b) where the test

results for turning using the same high-carbon tool steel brought to different hardness are

shown. As shown, the optimal cutting speed changes with the hardness and metallurgical

structure of the work material (Fig. 4.11(a)) while the optimal cutting temperature remains

the same (Fig. 4.11(b)).

The summary of the considered consequences is as follows:

The optimal cutting temperature depends upon only the compositions of the tool and

work materials, so it can be determined once, and then used to optimize various cutting

processes where the same combination of tool/work materials is used. This temperature

does not depend on the type of cutting operation, tool geometry, parameters of machining

regime, particular type and method of application of the cutting ﬂuid, etc.

200

100

0 204060n (m/min)

q(°C)

opt

1000

800

600

300

L (m)

= 90mm

45mm

27mm

Fig. 4.10. Inﬂuence of cutting speed on the cutting temperature and the total length of the tool path

in machining workpiece of three different diameters in turning. Work material – Haynes 263 alloy

(29% Cr, 2.5% Ti), tool material – micrograin carbide M10 (94% WC, 6% Co), depth of cut

= 0.25 mm, cutting feed f = 0.09 mm/rev, tool life criterion – radial tool wear VB

= 30 µm.