Atkinson K. An Introduction to Numerical Analysis
Подождите немного. Документ загружается.


THE TRAPEZOIDAL
RULE
AND SIMPSON'S RULE 259
Chapter
1],
p
1
(x) =
f(a)
+
(x-
a)f'(a)
R
2
(X)
=
fx
(X
- t )
f"
( t )
dt
a
Note that from (5.1.3),
(5.1.19)
for any two functions
F,
G E C[ a, b
].
Thus
since
E
1
(p
1
)
= 0 from (5.1.4). Substituting,
f
hjx
( b - a ) Jh
=
(x-
t)f"(t)
dt-
--
(b-
t)f"(t)
dt
a a 2 a
In general for any integrable function G(x,
t),
t Jx G(x, t) dtdx = t
tG(x,
t)
dxdt
a a a t
(5.1.20)
Thus
f
h
jh
(b-
a)Jh
E
1
(R
2
)
= a
f"(t)
1
(x-
t)
dxdt-
-
2
- a
(b-
t)f"(t)
dt
Combining integrals and simplifying the results,
1
fb
E
1
(!)
=-
f"(t)(t-
a)(t-
b)
dt
2 a
(5.1.21)
For the composite trapezoidal rule (5.1.5),
En(!)=
fbK(t)f"(t)
dt
a
(5.1.22)
i
--------------------
-------------
--------
--
..
--
--------
----··--·---------
j = 1, 2,
...
, n (5.1.23)
The formulas (5.1.21) and (5.1.22) are called the
Peano kernel formulation of the

i
I
--
_/
260 NUMERICAL INTEGRATION
error, and
K(t)
is called the Peano kernel. For a more general presentation, see
Davis (1963, chap.
3).
As a simple illustration of its
use,
take bounds in (5.1.22) to obtain
(5.1.24)
If
f"(t)
is very peaked, this may give a better bound on the error than (5.1.7),
because in (5.1.7)
we
generally must replace
1/"('IJ)I
by
11/"lloo·
For
Simpson's rule, use Taylor's theorem to write
11x
3
R
4
(x)
=-
(x-
t)
[<
4
>(t) dt
6 a
As before
and
we
the!l calculate
EiR
4
)
by direct substitution and simplification:
This yields
£
2
(!)
=
tK(t)[<
4
>(t) dt
a
{
1 3
-(t-
a)
(3t-
a-
2b)
K(t)
=
72
1 3
-.
(b-t)(b+2a-3t)
72
a+b
a
5.
t
5.
-
2
-
a+b
-2-
5,_
t
5,_
b
A graph
of
K(t)
is given in Figure
5.3.
By
direct evaluation,
b-a
h=--
2
{5.1.25)
{5.1.26)
As with the composite trapezoidal method, these results extend easily to the
composite
Simpson rule.
The following examples are intended to describe more fully the behavior of
Simpson's
and
trapezoidal rules.

--·---··
--·--·
-·
--
-
·-·-----
--
-··
·-
--·-
-
THE TRAPEZOIDAL RULE AND SIMPSON'S RULE 261
y
Example 1.
a
Figure 5.3 The Peano kernel for
Simpson's rule.
2
j(x)
=
;r
3
v'X.
[a. b] = [0.
1].
I = 9
Table 5.4 gives the error for increasing values of n. The derivative j<
4
l(x)
is
singular at x =
0,
and thus the formula (5.1.17) cannot be applied to this case. As
an alternative,
we
use the generalization of (5.1.25) to the composite Simpson rule
to obtain
Thus the error should decrease by a factor of 16 when
h
is
halved (i.e., n
is
doubled). This also gives a fairly realistic bound on the error. Note the close
agreement
of
the empirical values of ratio with the theoretically predicted values
of 4 and 16, respectively.
2.
1
f(x)
=
1
(
)2
+
x-'IT
[a,
b]
= [0,5]
I = 2.33976628367
Table
5.4 Trapezoidal, Simpson integration:
case
(1)
Trapezoidal Rule
Simpson's Rule
n Error
Ratio Error Ratio
2
-7.197-
2
3.96
-3.370-3
14.6
4
-1.817-
2
-2.315-
4
8
-4.553-
3
3.99
-1543-5
15.0
4.00
15.3
16
-1.139-
3
-1.008-6
32
-2.848-4
4.QO
-6.489-
8
15.5
4.00
i5.7
64
-7.121-
5
4.00
-.4.141-9
15.8
128
-1.780-
5
-2.626-
10
-----------------
-
-·
----------·--·------·
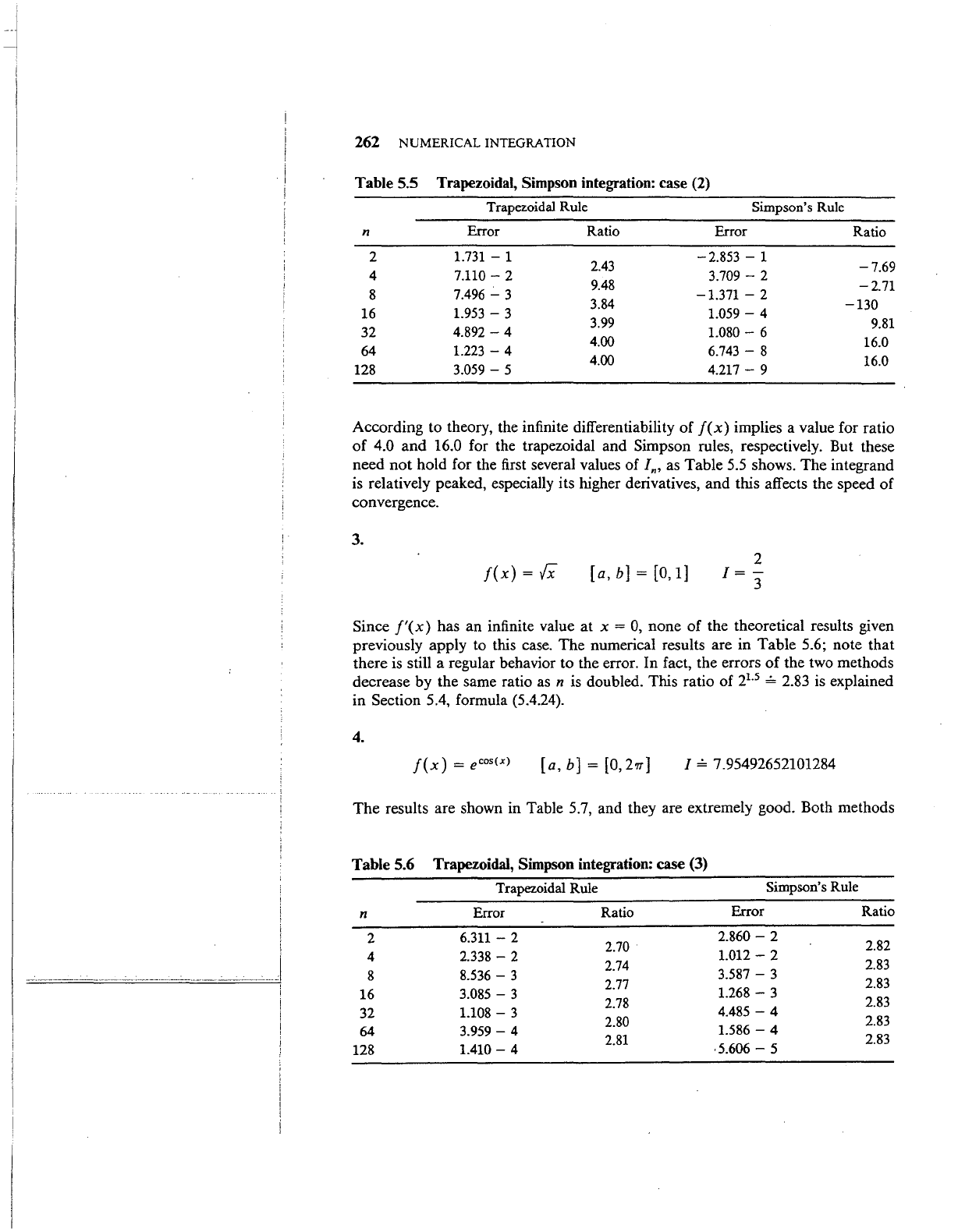
262 NUMERICAL INTEGRATION
Table 5.5
Trapezoidal,
Simpson
integration:
case
(2)
Trapezoidal Rule
Simpson's Rule
n Error Ratio Error
Ratio
2
1.731
- 1
2.43
-2.853-
1
-7.69
4
7.110-
2
3.709-
2
8
7.496
.:...
3
9.48
-1.371-
2
-2.71
16
1.953-
3
3.84
1.059-
4
-130
32
4.892-
4
3.99
1.080-
6
9.81
64
1.223-
4
4.00
6.743-
8
16.0
128
3.059-
5
4.00
4.217-
9
16.0
According to theory, the infinite differentiability
of
f(x)
implies a value for ratio
of
4.0
and
16.0 for the trapezoidal
and
Simpson rules, respectively. But these
need
not
hold for the first several values
of
In, as
Table
5.5 shows.
The
integrand
is relatively peaked, especially its higher derivatives,
and
this affects the speed
of
convergence.
3.
f(x)
=IX
[a,b]=[0,1]
2
I=-
3
Since
f'(x)
has an infinite value
at
x = 0,
none
of
the theoretical results given
previously apply to this case.
The
numerical results are in
Table
5.6; note
that
there
is still a regular behavior
to
the error.
In
fact, the errors
of
the two methods
decrease
by
the same ratio as n is doubled. This ratio
of
21.
5
= 2.83 is explained
in Section 5.4, formula (5.4.24).
4.
J(x)
=
ecos(x)
[a,
b]
= [0,277]
I=
7.95492652101284
The
results are shown in Table 5.7, and they are extremely good. Both methods
Table 5.6
Trapezoidal,
Simpson
integration:
case (3)
Trapezoidal Rule
Simpson's Rule
n
Error
Ratio
Error
Ratio
2
6.311-
2
2.70.
2.860-
2
2.82
4
2.338-
2
1.012-
2
2.83
2.74
3.587-
3
8
8.536-
3
2.77
2.83
16
3.085-
3
1.268-
3
2.78
2.83
32
1.108-
3
4.485-
4
2.83
2.80
64
3.959-
4
1.586-
4
2.83
128
1.410-
4
2.81
·5.606-
5

NEWTON-COTES INTEGRATION FORMULAS 263
Table 5.7 Trapezoidal, Simpson integration: case (4)
Trapezoidal Rule Simpson's Rule
n
Error
Ratio
Error
Ratio
2
-1.74
5.06E + 1
7.21E-
1
4
-3.44E-
2
5.34E-
1
1.35
8
-1.25E-
6
2.75E
+ 4
1.15E-
2
4.64E
+ 1
16
<
l.OOE-
14
> 1.25E + 8
4.17E-
7
2.76E
+ 4
<
l.OOE-
14
> 4.17E + 7
are very rapidly convergent, with the trapezoidal rule superior to Simpson's rule.
This illustrates the excellent convergence of the trapezoidal rule for periodic
integrands; this is analyzed in Section 5.4. An indication of this behavior can
be
seen from the asymptotic error terms (5.1.9) and (5.1.18), since both estimates
are
zero
in
this case
of
f(x).
5.2 Newton-Cotes Integration Formulas
The
simple trapezoidal rule (5.1.2)
and
Simpson's rule (5.1.13) are the first two
cases
of
the Newton-Cotes integration formula.
For
n
~
1, let h =
(b-
a)jn,
xj
=
a+
jh
for j =
0,
1,
...
, n. Define
In(/)
by replacing
f(x)
by its interpolat-
ing polynomial Pn(x)
on
the nodes x
0
,
x
1
;
•••
, xn:
(5.2.1)
Using the Lagrange formula (3.1.6) for Pn(x),
(5.2.2)
with
wj,n=
J\.n(x)dx
j=0,1,
...
,n
a
(5.2.3)
Usually we suppress the subscript n and write
just
wj.
We have already
calculated the cases n = 1 and
2.
To
illustrate the calculation
of
the weights, we
give the case
of
w
0
for n =
3.
A change
of
variable simplifies the calculations. Let x = x
0
+
p.h,
0
~
p.
~
3.

i
I
-~··----·--·~·-·-------~~-~------
-~-~---------~~--~-·
_,
___
_j
I
!
I
'
264
NUMERICAL
INTEGRATION
Then
1
13
=
--
(JL-
1)h(p.-
2)h(p.-
3)h.
hdp.
6h
3
0
h
13
=
--
(p.-
1)(p.
-2)(p.-
3)
dp.
6 0
3h
wo=-
8
The
complete
formula for n = 3 is
(5.2.4)
and
is called
the
three-eighths rule.
For
the
error, we give the following theorem.
Theorem 5.1 (a)
For
n even, assume
f(x)
is n + 2 times continuously differen-
tiable
on
[a,
b]. Then
some
11
E [a, b] (5.2.5)
with
1
1n
C..=
p.
2
(p.-
1)
· · ·
(p.-
n)
dp.
n
(n
+ 2)! 0
(5.2.6)
(b)
For
n odd, assume
f(x)
is n + 1 times continuously differen-
tiable on
[a,
b
].
Then
some
11
E
[a,
b]
(5.2.7)
with
1
in
C=
p.(p.-1)···(p.-n)dp.
n
(n
+ 1)! o
Proof
We
sketch the proof for
part
(a), the most
important
case.
For
complete
proofs
of
both
cases, see Isaacson
and
Keller (1966, pp. 308-314).
From
(3.2.11),
En(/)
=I(/)
-In(/)
=
jb(x-
x
0
)(x-
x
1
)
• • •
(x-
xn)f[x
0
,
x
1
,
.•.
, xn, x] dx
a

NEWTON-COTES INTEGRATION FORMULAS 265
Define
w(x) =
jx(t-
x
0
) • · •
(t-
xJ
dt
a
Then
w(a)=w(b)=O
·
w(x)>O
for
a<
x < b
The proof that w(x) > 0 can be found
in
Isaacson and Keller (1966,
p.
309).
It
is
easy to show w(b) =
0,
since the integrand
(t-
x
0
) • • •
(t-
xn)
is
an odd function with respect to the middle node
xn
12
=
(a+
b)/2.
Using integration
by
parts and (3.2.17),
En(!)=
jbw'(x)f[x
0
,
...
,xn,x]dx
a
En(!)
= -
jb
w(x
)/[x
0
,
••.
, xn,
x,
x]
dx
a
Using the integral mean value theorem
and
(3.2.12),
En(!)=
-f[xo•····
xn, t
~]jbw(x)
dx
a
/(n+2)(TJ)
b x
= - ( ) j j
(t-
x
0
) • • •
(t-
xn)
dtdx
(5.2.8)
n+2!
a a
We change the order of integration and then use the change of variable
t = x
0
+
p.h,
0
~
p.
;5;
n:
=
-hn+J
f"p.(p.-
1)
· · ·
(p.-
n +
1)(p.-
n)
2
dp.
lo
.
Use the change of variable v = n -
p.
to give the result
jbw(x)
dx
~
-hn+J1n(n-
v)
· · ·
(1-
v)v
2
dv
a 0
Use the fact that n is even and combine the preceding with (5.2.8), to
obtain the result (5.2.5)-(5.2.6).
•

266 NUMERICAL INTEGRATION
Table 5.8 Commonly used Newton-Cotes formulas
h h h
3
11
= 1 J
f(x)
dx =
-[f(a)
+/(b)]-
-/"(0
trapezoidal rule
u 2
12
n=2
ft<x)dx=~[t(a)
+4/(a;b)
+f(b)]-
~/<
4
>aJ
Simpson'srule
n=3
h 3h
3h
5
J
f(x)
dx =
-[f(a)
+ 3f(a
+h)+
3f(h-
h)+
/(b)]-
-j<
4
>aJ
u 8 w
n=4
f
h 2h [
(a+
h)
]
8h
1
f(x)
dx
=-
7f(a)
+
32/(a
+h)+
12/
--
+
32/(h-
h)+
7f(h)
-
-j<
6
>W
u
45
2
945
For easy reference, the most commonly used Newton-Cotes formulas are
given
in
Table 5.8. For n =
4,
/
4
(/)
is
often called Boote's rule. As previously,
let
h =
(b-
a)jn
in the table.
Definition A numerical integration formula
i(f)
that approximates
J(f)
is
said to have degree
of
precision m
if
1.
f(f)
=!(f)
for all polynomials
f(x)
of
degree.:::;;
m.
2.
[(f)
=I=
!(f)
for some polynomial f of degree m +
1.
Example With n =
1,
3 in Table 5.8, the degrees of precision are also m = n =
1,3,
respectively. But with n = 2,4, the degrees of precision are
(m
= n + 1 =
3,
5,
respectively. This illustrates the general result that Newton-Cotes formulas
with an even index
n gain an extra degree of precision as compared with those of
an odd index [see formulas (5.2.5) and (5.2.7)].
Each Newton-Cotes formula can be used to construct a composite rule. The
most useful remaining one
is
probably that based
on
Boole's rule (see Problem
7).
We omit any further details.
Convergence discussion The next question of interest is whether
In(f)
con-
verges to
!(f)
as n
~
oo.
Given the lack of convergence
of
the interpolation
polynomials on evenly spaced nodes for some choices of
f(x)
[see (3.5.10)],
we
should expect some difficulties. Table 5.9 gives the results for a well-known
example,
!
4
dx
I=
--
= 2 ·
tan-
1
(4)::: 2.6516
-41
+ x
2
(5.2.9)
These Newton-Cotes numerical integrals are diverging; and this illustrates the
fact that the Newton-Cotes integration formulas
In(f)
in (5.2.2), need not
converge to
!(f).
To understand the implications of the lack of convergence of Newton-Cotes
quadrature for
(5.2.9),
we
first give a general discussion
of
the convergence of
numerical integration methods.

NEWTON-COTES INTEGRATION FORMULAS
267
Table5.9
Newton-Cotes example
(5.2.9)
n
Jn
2
5.4902
4
2.2776
6
3.3288
8
1.9411
10
3.5956
Definition Let .fF be a family
of
continuous functions on a given interval [a, b
].
We say
§is
dense in
C[a,
b] if for every f E
C[a,
b] and every
£ > 0, there
is
a function
f.
in
.fF
for which
Max
lf(x)-
f.(x)
I:::;;£
as,xs,b
(5.2.10)
Example 1. From the Weierstrass theorem [see Theorem 4.1], the set of all
polynomials is dense in
C[ a, b
].
2.
Let
n;;::
1, h =
(b-
a)jn,
xj
=a+
jh,
0
~}:::;;
n. Let
f(x)
be linear on
each of the subintervals [xj_
1
,
xj]. Define § to be the set of all such piecewise
linear
fup.ctions
f(x)
for all n. We leave to Prbblem
11
the proof that .fF is dense
in
C[a,
b].
Theorem
5.
2 Let
n
In(!)=
L Wj,nf(xj,n) n;;:: 1
j-0
be a sequence of numerical integration formulas that approximate
Let
.fF
be a family dense in
C[a,
b]. Then
all
fEC[a,b]
(5.2.11)
if and only if
1.
all
jE.fF
(5.2.12)
and
n
2.
B = Supremum L
lwj,nl
<
oo
n<!:l
j-0

268
NUMERICAL
INTEGRATION
Proof (a) Trivially, (5.2.11) implies (5.2.12). But the proof that (5.2.11) im-
plies
(5.2.13)
is
much
more difficult. It
is
an example of the principle
of
uniform boundedness, and it can be found in almost any text on func-
tional analysis;
for
example, see Cryer (1982, p. 121).
(b)
We
now
prove that (5.2.12) and (5.2.13) implies (5.2.11). Let
f E
C[
a,
b]
be
given,
and let
t:
> 0 be arbitrary. Using the assumption
that
.;F
is
dense in
C[
a, b
],
pick
f.
E
ff
such that
Then write
I(!)-
In(!)=
[I(!)
-/(f.)]
+
[I(f.)
-In(/.)]
+[In(!.)-
I,(!)]
It
is
straightforward to derive, using (5.2.13) and (5.2.14), that
IJ{f}-
In(!)
I:=;
IJ(f)-
J(f,)
I+
II{!.}-
Jn(f<)
I
+
IJn(J.}-
Jn(f)
I
(
::;
2
+II(!.)
-
!Jf.)
I
(5.2.14}
Using (5.2.12),
ln(f.)
~
!{f.)
as n
~
oo.
Thus for all sufficiently large
n,
say· n
~
n,,
Since
t:
was
arbitrary, this shows
ln(f)
~
/(f)
as
n
~
oo.
•
Since the Newton-Cotes numerical integrals
In(f)
do not converge to
/{f)
for
f(x)
=
1/(1
+ x
2
)
on [
-4,4],
it must follow that either condition (5.2.12) or
(5.2.13) is violated.
If
we
choose
!F
as the polynomials, then (5.2.12)
is
satisfied,
since
In(
p)
=
/(
p)
for any polynomial p
of
degree
::;
n. Thus (5.2.13) must be
false. For the Newton-Cotes formulas
(5.2.2),
n
Supremum L
lwj.nl
=
oo
n
j=O
Since
/{f)
=
ln(f)
for the special case
f(x)
==
1,
for any
n,
we
have
n
"w.
=
b-
a
1..-
J,n
j=O
n~1
(5.2.15)
(5.2.16)
