Atkinson K. An Introduction to Numerical Analysis

PROBLEMS 329

38. Evaluate the following singular integrals within the prescribed error toler-

ance.

Do

not

use

an automatic program.

(a)

fo

4

"

cos(u)log(u)

du £ =

10-

8

1

2/fT

( 1 )

(b)

·

0

x

2

sin

~

dx £ =

10-

3

(c)

(d)

{ cos

3

(x)

dx

op

( = 10-8

1

£ =

10-

5

a = 1 - -

'IT

39. Use an adaptive program (e.g., DQAGP) to evaluate the integrals of

Problem 38.

40. (a) Develop the product trapezoidal integration rule for calculating

!(!)

=

1

b/(x)adx

0 X

O<a:::;;1

Put the weights into a convenient form, analogous to (5.6.28) for the

product trapezoidal rule when

w(x)

=

log(x).

Also, give an error

formula analogous

to

(5.6.24).

(b) Write a simple program to evaluate the following integrals using the

results of part (a).

dx

(ii)

11--..,..-,--

0

sin(x

2

1")

Hint: For part (ii), first let u = x

2

1".

41. To show the ill-posedness of the differentiation of a function

y(t)

on an

interval

[0,

1],

consider calculating

x(t)

=

y'(t)

and

xn(t)

=

y;(t),

with

1

Yn(t)

=

y(t)

+

-tn

n

:2::

1

n

Recall the definition of ill-posed and well-posed problems from Section 1.6 .

. Use the preceding construction to show that the evaluation of

x(t)

is

unstable relative to changes in

y. For measuring changes in x and y, use

the maximum norm of (1.1.8) and (4.1.4).

42. Repeat the numerical differentiation example

of

(5.7.23) and Table 5.25,

using your own computer or hand calculator.

43. Derive error results for

DtJ(m)

in (5.7.10) relative to the effects of

rounding errors, in analogy with the results

(5.7.21)-(5.7.22) for

jjp>j(x).

Apply

it

to

f(x)

= ex at x =

0,

and compare the results with the actual

results

of

your own hand computations.

SIX

NUMERICAL METHODS

FOR

ORDINARY

DIFFERENTIAL

EQUATIONS

Differential equations are one

of

the most important mathematical tools used in

modeling problems in the physical sciences. In this chapter we derive and analyze

numerical methods for solving problems for ordinary differential equations. The

main form

of

problem that

we

study

is

the initial value problem:

y'

=

f(x,

y)

(6.0.1)

The

function

f(x,

y)

is to be continuous for all

(x,

y)

in some domain D

of

the

xy-plane, and

(x

0

,

Y

0

)

is

a point

in

D. The results obtained for (6.0.1) will

generalize

in

a straightforward way to both systems of differential equations and

higher order equations, provided appropriate vector and matrix notation is used.

These generalizations are discussed and illustrated in the next two sections.

We

say that a function

Y(x)

is

a solution on

(a,

b]

of (6.0.1) if for all

a~

x

~

b,

1.

(x,

Y(x))

ED:

2.

Y(x

0

)

= Y

0

•

3.

Y'(x)

exists and

Y'(x)

=

f(x,

Y(x)).

As notation throughout this chapter,

Y(x)

will denote the true solution of

whatever differential equation problem is being

cOnsidered:

Example

l.

The general first-order linear differential equation

is

y'

= a

0

(x)y

+

g(x)

as;,xs;,b

in which the coefficients a

0

(x)

and

g(x)

are assumed to be continuous on

(a,

b].

The

domain D for this problem is ·

D =

{(x,y)!a

~

x

s;,

b,

-oo

<y

<co}

.

The

exact solution of this equation can be found in any elementary differential

equations textbook [e.g., Boyce and Diprima (1986), p. 13]. As a special case,

consider

y'

= >.y +

g(x)

Os;,x<oo

(6.0.2)

333

[

I

-

-_I

I

l

I

i

I

334 NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS

with

g(x)

continuous on

[0,

oo). The solution that satisfies

Y(O)

= Y

0

is

given by

O~x<oo

(6.0.3)

This is used later to illustrate various theoretical results.

2.

The equation

y'

=

-y

2

is

nonlinear. One

of

its solutions is

Y(x)

= 0,

and

the remaining solutions have the form

1

Y{x) =

--

x+c

with

can

arbitrary constant. Note that

IY(-c)l

=

oo.

Thus the global smooth-

ness

of

j(x,

y)

=

-y

2

does not guarantee a similar behavior in the solutions.

To

obtain

some

geo~etric

insight for the solutions

of

a single first-order

differential equation,

we

can look at· the direction field induced by the equation

on

the xy-plane.

If

Y(x)

is

a solution that passes through

(x

0

,

Y

0

),

then the slope

of

Y(x)

at

(x

0

,

Y

0

)

is Y'(x

0

)

=

j(x

0

,

Y

0

).

Within the domain D of

f(x,

y),

pick

a representative set of points

(x,

y)

~d

then draw a short line segment with

slope

f(x,

y)

through each (x,

y).

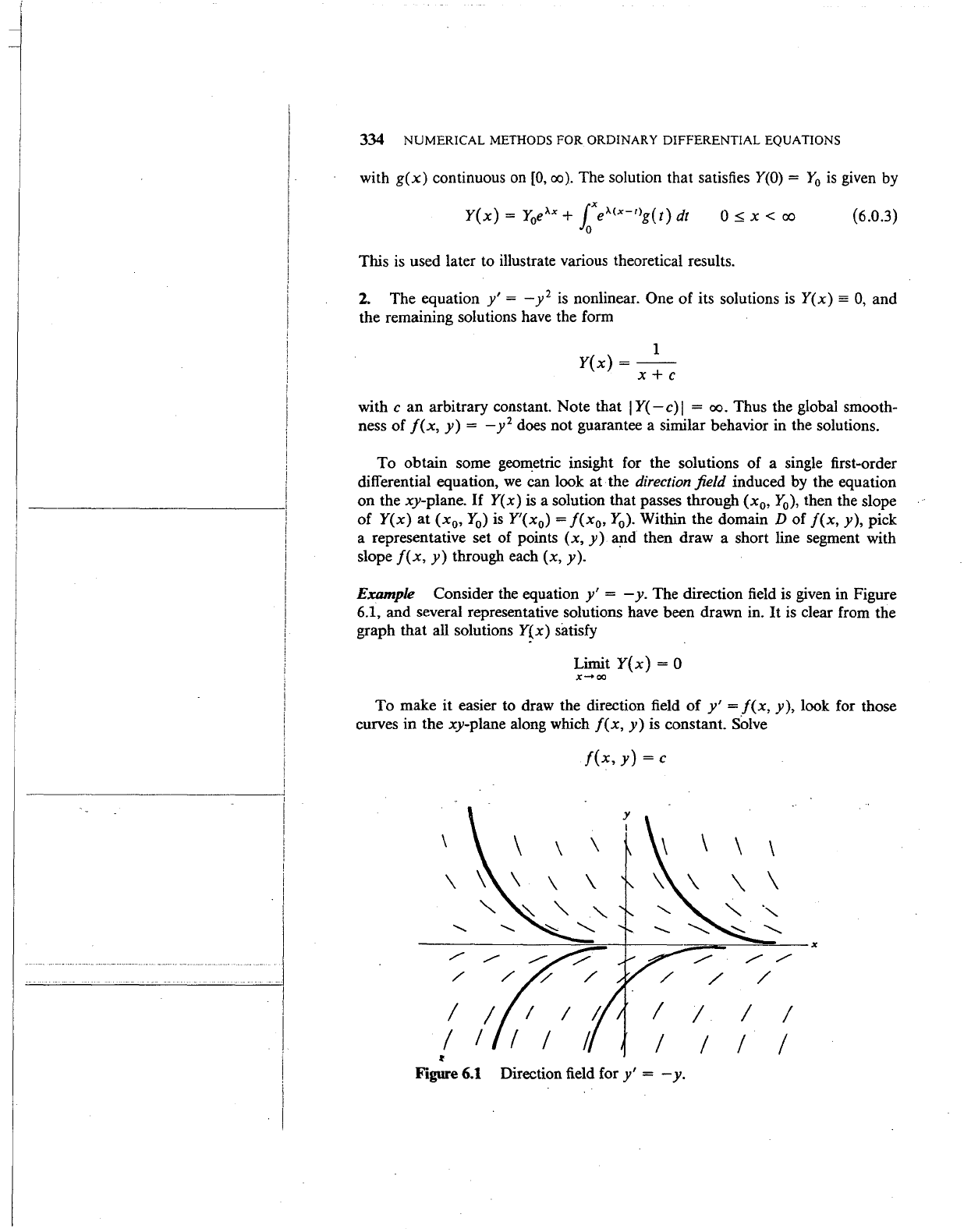
Example Consider the equation

y'

= - y. The direction field is given in Figure

6.1, and several representative solutions have been drawn in.

It

is clear from the

graph that all solutions

Y(x)

satisfy

Limit

Y(x)

= 0

X->CXl

To

make

it

easier to draw the direction field

of

y'

=

f(x,

y),

look for those

curves

in

the xy-plane along which

f(x,

y)

is constant. Solve

J(x,

y)

= c

y

I

\

\ \

\

........

..........

--x

/

I

~

Figure

6.1

Direction field for

y'

= -

y.

j

I

EXISTENCE, UNIQUENESS,

AND

STABILITY THEORY 335

y

Figure 6.2 · Direction

field

for

y'

= x

2

+ y

2

•

for various choices of

c.

Then each solution

Y(x)

of

y'

=

f(x,

y)

that intersects

the curve

f(x,

y)

= c satisfies

Y'(x)

= c at the point

of

intersection. The curves

f(x,

y)

=care

called level curves of the differential equation.

Example Sketch the qualitative behavior of solutions

of

The level curves of the equation are given by

c>O

which are circles with center (0,0) and radius

/C.

The

direction

field

with some

representative solutions is given in Figure

6.2.

Three circles are drawn, with

c =

~,

1,

4.

This

gives

some qualitative information about the solutions

Y(

x

),

and

occasionally this can be useful.

-"-'==~~=-==.c..-""-'-'----'=~'-"===-'·=i

6.1

Existence, Uniqueness, and Stability Theory

From the examples of the introduction it should

be

intuitive that

in

most cases

the initial value problem

(6.0.1) has a unique solution. Before beginning the

numerical analysis for

(6.0.1),

we

present some theoretical results for it. Condi-

tions are given to ensure that it has a unique solution, and

we

consider the

I

i

I

m••~j

336

NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS

stability of the solution

when

the initial data Y

0

and the derivative

f(x,

y)

are

changed by small amounts. These results are necessary in order to better

understand the numerical methods presented later. The domain

D will hence-

forth be assumed to satisfy the following minor technical requirement:

If

two

points

(x,

y

1

)

and

(x,

y

2

)

both belong to D, then the vertical line segment joining

them is also contained in

D.

Theorem 6.1 Let

/(x,

y)

be a continuous function of x and y, for all (x,

y)

in

D, and let

(x

0

,

Y

0

)

be an interior point of D. Assume

f(x,

y)

satisfies the Lipschitz condition

all (x, y

1

),

(x,

h)

in D (6.1.1)

for some K

~

0.

Then for a suitably chosen interval I =

[x

0

-

a, x

0

+ a], there

is

a unique solution Y(x) on I of (6.0.1).

Proof

The proof of this result can be found in most texts on the theory of

ordinary differential equations [e.g., see Boyce and Diprima

(1986),

p.

95].

For that reason,

we

omit it. •

Showing the Lipschitz

is

straightforward if

aj(x,

y)/

a y exists and

is

bounded

on

D. Simply let

K=

Max

.

laj(x,y)l

(x,_v)ED

ay

(6.1.2)

Then using the mean value theorem

for some

t between y

1

and y

2

•

Result (6.1.1) follows immediately using (6.1.2).

Example

The following

two

examples illustrate the theorem.

1.

Consider

y'

= 1 + sin (

xy)

with

D = {

(X'

y

)I

0

~

X

~

1'

-

00

< y <

00}

To

compute the Lipschitz constant

K,

use (6.1.2). Then

aj(x,y)

---

= x ·

cos(xy)

ay

K=l.

Thus for any

(x

0

,

Y

0

)

with 0 < x

0

< 1, there is a solution

Y(x)

to the associated

initial

value problem on some interval

[x

0

-

a, x

0

+ a] c

[0,

1].

EXISTENCE, UNIQUENESS, AND STABILITY THEORY

337

2.

Consider the problem

y(O)

= 1

for any constant a >

0.

The solution is

a2

Y(x)

= 2 2

a - x

-a<

x

<a

The solution exists on only a small interval if a is small. To determine the

Lipschitz constant,

we

must calculate

aj(x,

y)

4xy

ay

a

2

To have a finite Lipschitz constant on D, the region D must be bounded in x

and

y,

say - c

~

x

~

c and - b

~

y

~

b. The preceding theorem then states that

there is a solution

Y(x)

on some interval

-a~

x

~a,

with a

~

c.

· Lest it be thought that

we

can evaluate .the partial derivative at the initial

point

(x

0

,

Y

0

)

=

(0,

1) and obtain sufficient information to estimate the Lipschitz

constant

K,

note that

for any

a>

0.

af(0,1)

---=0

ay

Stability of the solution The stability

of

the solution

Y(x)

is

examined when the

initial value problem

is

changed by a small amount. This is related to the

discussion of stability in Section

1.6

of

Chapter 1. We consider the perturbed

problem

y'

=

f(x,

y)

+

8(x).

y(xo)

==

Yo+

t:

{6.1.3)

with the same hypotheses for

f(x,

y)

as in Theorem 6.1. Furthermore,

we

assume

8(x)

is continuous for

all

x such that

(x,

y)

ED

for some

y.

The problem

(6.1.3) can then be shown to have a unique solution, denoted by

Y(x;

8,

t:).

Theorem 6.2 Assume the same hypotheses as in Theorem 6.1. Then the problem

(6.1.3) will have a unique solution

Y(x;

8,

t:)

on an interval

[x

0

-

a, x

0

+a],

some

a>

0,

uniformly for all perturbations

t:

and

8(x)

that satisfy

for

t:

0

sufficiently small.

In

addition, if

Y(x)

is

the solution of the

!

I

...

I

338 NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS

unperturbed problem, then

Max

IY(x)-

Y(x; 8,

€)

I~

k[\£1

+

ajjSII"']

(6.1.4)

lx-xol5a

with k =

1/(1

-

aK),

using the Lipschitz constant K of (6.1.1).

Proof

The

derivation

of

(6.1.4) is much the same as the proof of Theorem 6.1,

and

it can be found in most graduate texts

on

ordinary differential

equations.

•

Using

this result, we can say that the initial value problem (6.0.1)

is

well-posed

or

stable,

in

the sense

of

Section 1.6 in Chapter

1.

If

small changes are made in

the differential equation

or

in the initial value, then the solution will also change

by a small amount.

The

solution Y depends continuously on the data of the

problem, namely the function

f and the initial

data

Y

0

.

It was pointed out in Section 1.6 that a problem could be stable but

ill-conditioned with respect to numerical computation. This is true with differen-

tial equations, although it does not occur often in practice.

To

better

under_stand

when this may happen,

we

estimate the perturbation in Y due to perturbations in

the problem.

To

simplify our discussion,

we

consider only perturbations £ in the

initial value

Y

0

;

perturbations

S(x)

in the equation enter into the final answer in

.much the same way, as indicated in (6.1.4).

Perturbing the initial value

Y

0

as in (6.1.3), let Y(x;

£)

denote the perturbed

solution. Then

Y'(x; e) =

j(x,

Y(x; e))

Y(x

0

;

€)

= Y

0

+ €

X

0

-

0:

:5

X

:=;·

Xn + 0:

(6.1.5)

Subtract

the

corresponding equations

of

(6.0.1) for

Y(x),

and let

Z(x;

e) =

Y(x;

e) - Y(x).

Then

Z'(x;

£)

=

f(x,

Y(x;

!))

-

f(x,

Y(x))

8j(x,

Y(x))

="'

ay

Z(x;

!)

( 6.1.6)

and

Z(x

0

;

€)

=£.The

approximation (6.1.6) is valid when Y(x;

€)

is

sufficiently

close to

Y(x),

which it is for small values

of£

and

small intervals [x

0

-

a,

x

0

+ a].

We can easily solve the approximate differential equation of (6.1.6), obtaining

[

.

x8/(t,

Y(t))

l

Z(x;

€)

,;,

€ • exp f a dt

xo Y

If

the partial derivative satisfies

8f(t,

Y(t))

----~0

ay

(6.1.7)

(6.1.8)

'

_\

EXISTENCE, UNIQUENESS,

AND

STABILITY THEORY

339

then

we

have that

Z(x,

£)probably remains bounded

by£

as

x increases. In this

case, we say the initial value problem

is

well-conditioned.

As an example

of

the opposite behavior, suppose we consider

y'=Ay+g(x)

y(O)

= Y

0

( 6.1.9)

with A >

0.

Then

8fj8y

=A,

and

we

can calculate exactly

Thus the change in Y(x) becomes increasing large as

x increases.

Example

The

equation

y'

= 100y - 101e-x

y(O)

= 1 (6.1.10)

has the solution

Y(x)

=e-x.

The perturbed problem

y'

= 100y - 101e-x

y(O)

= 1 + £

has the solution

Y(x;

€)

=e-x+

t:elOOx

which rapidly departs from the true solution. We say (6.1.10) is an ill-conditioned

problem.

=

For

a problem to be well-conditioned,

we

want the integral

f

x

8f(t,

Y(t))

----dt

Xo

ay

to

be

bounded from above by zero

or

a small positive number, as x increases.

Then the perturbation

Z(x;

£)will be bounded

by

some constant times_£, with

- the constant

not

too large. ·

In

the case that (6.1.8) is satisfied,

but

the partial derivative is large in

magnitude, we will have that

Z(x;

€)

--4

0 rapidly as x increases. Such equations

are considered well-conditioned,

but

they may also be troublesome for most of

the numerical methods of this chapter. These equations are called

stiff

differential

equations,

and

we will return to them later in Section 6.9. ·

Systems of differential equations

The

material

of

this chapter generalizes

to

a

system

of

m first-order equations, written

(6.1.11)

I

. . . . . I

-

··-··

··-

····-

··-

340

NUMERICAL

METHODS FOR ORDINARY

DIFFERENTIAL

EQUATIONS

This

is

often made to look like a first-order equation by introducing vector

notation. Let

[

y

1

(x)

j

y(x)

= ;

[

yl.O

j

Y

0

= ; (6.1.12)

Ym(x)

Ym,O

The system (6.1.11) can then be written as

y' =

f(x,

y)

(6.1.13)

By

introducing vector norms to replace absolute values, virtually all of the

preceding results generalize to this vector initial value problem.

For higher order equations, the initial value problem

y<m>

=

f(x,

y, y',

...

,

y<m-1>)

y(xo)

=

Yo,

...

,

y<m-1>(xo)

=

Yo(m-1)

(6.1.14)

can be converted to a first-order system. Introduce the new unknown functions

Y1

= Y

Yz

=

y'

• · · · •

Ym

=

y<m-

1

)

•

These functions satisfy the system

Y~

=

Yz

Y.:.-1

=

Ym

Example

The

linear second-order equation

y"

= a

1

(x)y'

+ a

0

(x)y

+

g(x)

becomes

Yl(xo) =

Yo

h(xo)

=

Yo

In

vector form with

A(x)

denoting the coefficient matrix,

y'

= A ( x )y +

G(

x)

a linear system

of

first-order differential equations.

(6.1.15)

Atkinson K. An Introduction to Numerical Analysis

Подождите немного. Документ загружается.