Atkinson K. An Introduction to Numerical Analysis

......

··-···

...

---------

...

.. j

EULER'S METHOD 351

Usually rounding error

is

not a serious problem. However, if the desired

accuracy

is

close to the best that can be attained because of the computer word

length, then greater attention must be given to the effects due to rounding.

On an

IBM mainframe computer (see Table 1.1) with double precision arithmetic, if

h

~

.001, then the maximum of

ujh

is

2.2

X

10-

13

, where u

is

the unit round.

Thus the rounding error

will

usually not present a significant problem unless very

small error tolerances are desired. But in single precision with the same restric-

tion

on

h, the maximum of

ujh

is

0.5 X 10-4,

and

with

an

error tolerance of this

magnitude (not an unreasonable one), the rounding error will be a more signifi-

cant

factor.

Example We solve the problem

y'=

-y+2cos(x)

y(O)

= 1

whose true solution

is

Y(x)

=sin

(x)

+ cos(x). We solve it using Euler's method,

with three different forms

of

arithmetic: (1) fqur-digit decimal floating-point

arithmetic with chopping; (2) four-digit decimal floating-point arithmetic with

rounding; and (3) exact,

or

very high-precision, arithmetic.

In

the first two cases,

the unit rounding errors are

u =

.001

and u = .0005, respectiYely. The bound

(6.2.32) applies to

cas_es

1 and

2,

whereas case 3 satisfies the theoretical bound

(6.2.24). The errors for the three forms of Euler's method are given in Table 6.3.

The errors for the answers obtained using decimal arithmetic are based on the

true answers

Y(

x)

rounded to four digits.

For

the case of chopped decimal arithmetic, the errors are beginning to be

affected with

h = .02; with h =

.01,

the chopping error has a significant effect

on

Table

6.3 Example

of

rounding effects in Euler's

method

Chopped

Rounded

Exact

h

X

Decimal

Arithmetic

.04

1

-l.OOE-2

-1.70E-

2

-1.70E-

2

-1.17E-

2

1.83E-

2

-1.83E-

2

3

-1.20E-

3

-2.80E-

3

-2.78E-

3

4

l.OOE- 2

1.60E-

2

1.53E-

2

5

1.13E-

2

1.96E-

2

1.94E-

2

.02

1

7.00E-

3

-9.00E-

3

-8.46E-

3

2

4.00E-

3

-9.10E-

3

-9.13E-3

3

2.30E-

3

-1.40E-

3

-1.40E-

3

4

-6.00E-

3

8.00E-

3

7.62E-

3

5

-6.00E-

3

8.50E-

3

9.63E-

3

.01

1

2.80E-

2

-3.00E-

3

-4.22E-

3

2

2.28E-

2

-4.30E-

3

-4.56E-

3

7.40E-

3

-4.00E-

4

-7.03E-

4

-2.30E-

2

3.00E-

3

3.80E-

3

5

-2.41E-

2 4.60E

-3

4.81E-

3

I

H-

••

---------

•••

•d-

H

---·--

---··-

••

I

352 NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS

the total error. In contrast, the errors using rounded arithmetic are continuing to

decrease, although the h =

.01

case is-affected slightly. With this problem, as with

most others, the use

of

rounded arithmetic is far superior to that

of

chopped

arithmetic.

Asymptotic

error

analysis

An

asymptotic estimate

of

the error in Euler's

method is derived, ignoring any effects due to rounding. Before beginning, some

special

notation

is

necessary to simplify the algebra in the analysis.

If

B ( x,

h)

is a

function defined for x

0

:s:

x

~

b

and

for-all sufficiently small h, then the notation

B(x,

h)=

O(hP)

for some p > 0, means there is a constant c such

that

I B (

x,

h) 1

~

ch P

(6.2.34)

for all sufficiently small h.

If

B depends on h only, the same kind of bound is

implied.

Theorem 6.4 Assume

Y(x)

is the solution

of

the initial value problem (6.0.1)

and

that it

is

three times continuously

differentiable~

Assume

Bf(x,

y)

f,(x,y)=

By

are continuous

and

bounded for x

0

:S:

x

:S:

b,

-

oo

< y <

oo.

Let

the initial value

fh(X

0

)

satisfy

(6.2.35)

Usually this error is zero and thus

1>

0

= 0.

Then the error in Euler's method (6.2.3) satisfies

(6.2.36)

where

D(x)

is the solution

of

the linear initial value problem

D'(x)

=

f,(x,

Y(x))D(x)

+ t Y"(x)

D(x

0

)

= o

0

(6.2.37)

Proof Using Taylor's theorem,

for some xn

:S:

~"

~

xn+l·

Subtract (6.2.3)

and

use (6.2.2) to obtain

(6.2.38)

i

.,

......

····----

--

-·

-··

..

·-··-··-

····-·

--l

EULER'S METHOD 353

Using Taylor's theorem on

f(x,,

y,), regarded

as

a function of y,.

j(x,,

yJ

=

j(x,,

Y,) +

(y,-

Y,).0.(x,,

Y,}

+

!(y,-

Y,ff}·y(x,,

f,)

for some

f,

between

y,

and Y,. Using this in (6.2.38),

h2

en+l

=

[1

+

hf~(x,,

Y,)]en +

2Y"(x,)

+

B,

( 6.2.39)

Using (6.2.16)

(6.2.40)

Because

B,

is small relative to the remaining terms in (6.2.39),

we

find

the dominant part of the error by neglecting

B,. Let

g,

represent the

dominant part

of

the error.

It

is

defined implicitly by

h2

.

gn+l

=

[1

+

hfv(x,,

Y,)]g, +

2Y"(x,)

( 6.2.41)

with

(6.2.42)

the dominant

part

of the initial error (6.2.35). Since

we

expect

g,,;,

e,.

and since

e,

=

0(

h),

we

introduce the sequence {

8,}

implicitly by

(6.2.43)

Substituting into (6.2.41), canceling

h

and

rearranging,

we

obtain

x

0

:::;;

x,:::;; b (6.2.44)

I

The initial value 8

0

from (6.2.35) was defined as independent of

h.

The equation (6.2.44)

is

Euler's method for solving the initial value

problem (6.2.37); thus from Theorem 6.3,

(6.2.45}

Combining this with (6.2.43),

{6.2.46)

To complete the proof,

it

must be shown that

g,

rs

indeed the

principal part

of

the error e

,.

Introduce

(6.2.47)

I

---

-

------------

____

I

354

NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS

Then k

0

= e

0

-

g

0

=

O(h

2

)

from (6.2.35) and (6.2.42). Subtracting

(6.2.41) from (6.2.39), and using (6.2.40),

kn+t

=

[1

+ h/y(x,, Y,)]k, + B,

lkn+tl

::;

(1

+

hK

)lk,l +

0(

h

3

)

This is of the form of (6.2.20) in the proof of Theorem

6.3,

with the term

h-r(h)

replaced by

O(h

3

).

Using the same derivation,

(6.2.48)

Combining ( 6.2.46)-( 6.2.48),

which proves (6.2.36).

•

The function

D(x)

is rarely produced explicitly,

but

the form of the error

(6.2.36) furnishes useful qualitative information.

It

is

often used

as

the basis for

extrapolation procedures, some of which are discussed in later sections.

Example Consider the problem

y'

=

-y

y(O)

= 1

with the solution

Y(x)

= e-x. The equation for

D(x)

is

D'(x) =

-D(x)

+

te-x

D(O) = 0

and

its solution

is

D(x)

=

txe-x

This gives the following asymptotic formula for the error in Euler's method.

(6.2.49)

Table 6.4 contains the actual errors and the errors predicted by (6.2.49) for

h = .05. Note then the error decreases with increasing

x,

just

as

with the solution

Y(x).

But the relative error increases linearly with x,

Y(x,)-

Yh(x,)

Y(x,)

h

,;,

-x

2 ,

Also, the estimate (6.2.49)

is

much better than the bound given by (6.2.13) in

__

j

EULER'S METHOD 355

Table

6.4 Example (6.2.49)

of theorem 6.4

x,

Y,

-

Yn

hD(x,)

.4

.00689

.00670

.8

.00920 .00899

1.2

.00921

.00904

1.6 .00819

.00808

2.0

.00682 .00677

Theorem 6.3. That bound is

and it increases exponentially with

x,.

Systems of equations To simplify the presentation, we will consider only the

following system of order

2:

y{

=

/1

(X'

Yl'

Y2)

y~

= f2(x,

Y1,

Y2)

Yl(xo) =

Y1,0

Y2(xo)

=

Y2,o

(6.2.50)

The generalization to higher order systems

is

straightforward. Euler's method for

solving

(6.2.50)

is

{6.2.51)

a clear generalization of (6.2.3).

All of the preceding results of this section will generalize to (6.2.51), and the

form of the generalization

is

clear if

we

use the vector notation for (6.2.50) and

(6.2.51),

as

given in (6.1.13) in the last section. Use

y'

= f{x,y)

In

place of absolute values, use the norm (1.1.16) from Chapter 1:

IIYII

=

MaxiY;I

i

To generalize the Lipschitz condition (6.2.12), use Taylor's theorem (Theorem

1.5) for functions of several variables to obtain

llf(x,z) - f(x,y)JI5:

Kllz-

Yll

{6.2.52)

a[;(x,

wl,

w2)

K=

Max_E

Max

i j x

0

s,xs,b

-oo<w

1

,

"'l<oo

(6.2.53)

I

i

!

I

i

I

-

----

---

--

_j

356 NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS

The

role

of

aj(x,

y)jay

is

replaced by the Jacobian matrix

(6.2.54)

As an example, the asymptotic error formula (6.2.36) becomes

(6.2.55)

with

D(x)

the solution of the linear system

D'(x)

= fy(x,

Y(x))D(x)

+ fY"{x)

(6.2.56)

using the preceding matrix fy(x, y).

Exampk Solve the pendulum equation,

8"(

t) =

-sin

(

8(

t))

7T

8{0)

= 2

8'{0)

= 0

Convert this to a system by letting y

1

=

8,

y

2

=

(}',

and replace the variable t by

x. Then

Y{

=

Y2

y

2

(0) = 0

(6.2.57)

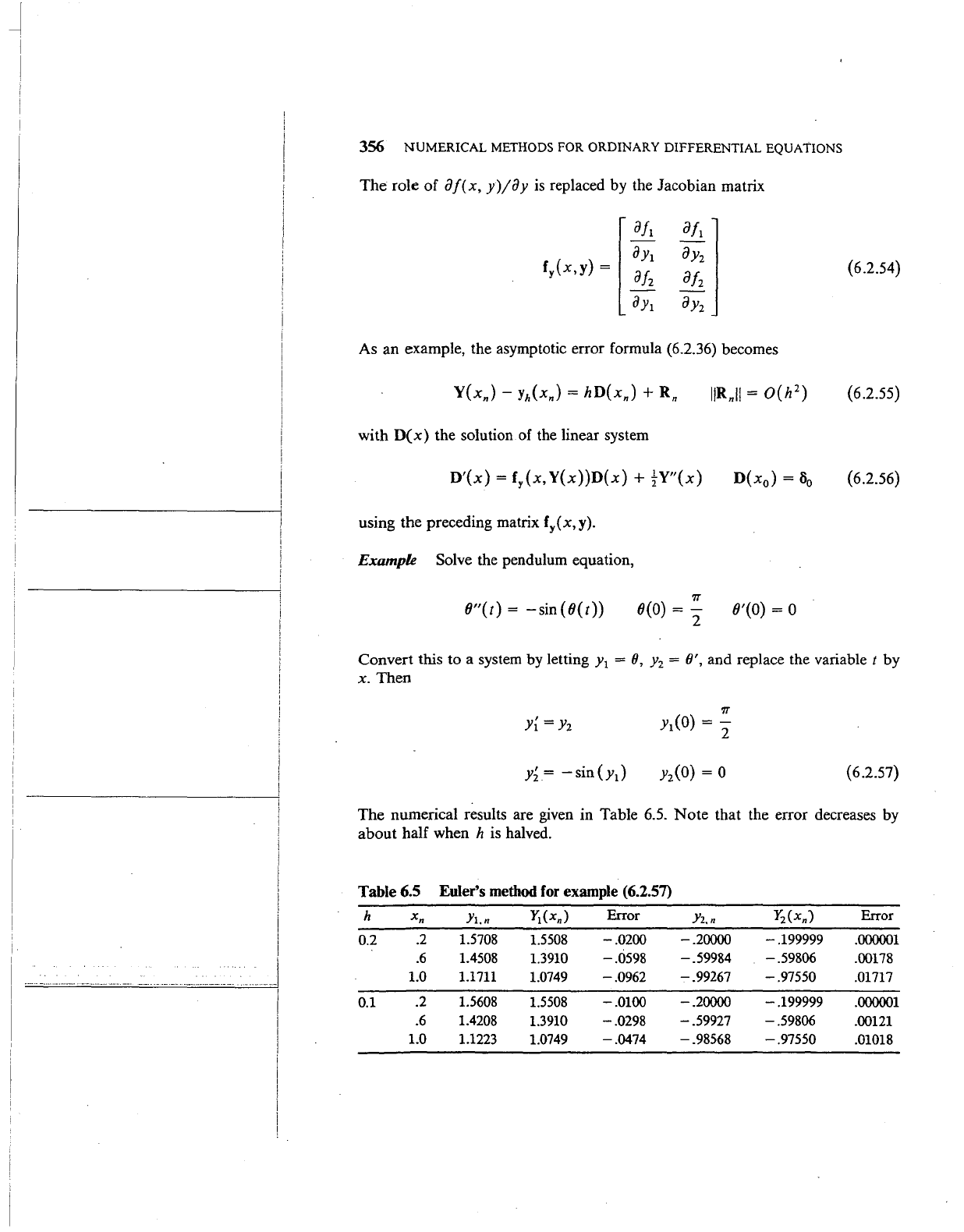
The numerical results are given in Table 6.5. Note that the error decreases by

about half when h is halved.

Table 6.5

Euler's

method

for

example (6.2.57)

h

Xn

Y!,n

Y

1

(xn)

Error

Y2,n

J2(xn)

Error

0.2

.2

1.5708

1.5508

-.0200

-.20000

-.199999

.000001

.6

1.4508

1.3910

-.0598

-.59984

-.59806

.00178

1.0

1.1711

1.0749

-.0962

-.99267 -.97550

.01717

0.1

.2 1.5608

1.5508

-.0100

-.20000

-.199999

.000001

.6

1.4208

1.3910

-.0298

-.59927 -.59806

.00121

1.0 1.1223 1.0749

-.0474

-.98568 -.97550

.01018

MULTISTEP METHODS 357

6.3 Multistep

Methods

This section contains an introduction to the theory of multistep methods. Some

particular methods are examined in greater detail in the following sections. A

more complete theory is given in Section

6.8.

As before, let h > 0 and define the nodes by xn = x

0

+ nh, n

~

0.

The

general form

of

the multistep methods to be considered is

p p

Yn+l

= L ajYn-j + h L

bJ(xn-j•

Yn-J

n~p

(6.3.1)

j=O

j=

-1

The

coefficients a

0

,

•••

,

aP,

b_

1

,

b

0

,

.••

,

bP

are constants, and p

~

0.

If

either

a P

=I=

0 or

bP

=I=

0, the method is called a p + 1 step method, because p + 1

previous solution values are being used to compute

Yn+l·

The values y

1

,

•••

,

Yp

must

be

obtained

by

other means; this

is

discussed in later sections. Euler's

method is

an

example of a one-step method, with p = 0 and

b

0

= 1

If

b _

1

= 0, then

Yn+

1

occurs on only the left side of equation (6.3.1

).

Such

formulas are called

explicit methods.

If

b_

1

=I=

0, then

Yn+l

is present on both

sides

of

(6.3.1)

and

the formula is called an implicit method. The existence of the

solution

Yn+l•

for all sufficiently small h, can

be

shown by using the fixed-point

theory

of

Section 2.5. Implicit methods are generally solved by iteration, which

are discussed in detail for the trapezoidal method in Section 6.5.

Example

1.

The

midpoint method

is

defined

by

Yn+l

=

Yn-l

+

2hj(xn,

Yn)

n~1

(6.3.2)

and it is

an

explicit two-step method.

It

is examined in Section 6.4.

·

2.

The

trapezoidal method

is

defined by

h

Yn.+l

=

Yn

+

l[J(xn,

Yn)

+

f(xn+l•

Yn+l)]

n~O

( 6.3.3)

It

is

an

implicit one-step method, and it is discussed in Sections

6.5

and 6.6.

For

any differentiable function

Y(x),

define the truncation error for integrat-

ing

Y'(x)

by

T,(Y)

~

Y(x.+,)-

Lt

a

1

Y(x.-)

+hI~'

b

1

Y'(x._)]

n

~

p (6.3.4)

Define the function

Tn(Y)

by

( 6.3.5)

I

i

I

i

I

--------------------------

------

--------

__

-

___

_1

I

358 NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS

In order to prove the convergence of the approximate solution {

Yn

I x

0

:::;;;

xn

:::;;;

b}

of (6.3.1) to the solution

Y(x)

of the initial value problem (6.0.1), it

is

necessary

to have

T(h) = Max

l'~"n(Y)

I~

0

xP:;,x.s,b

as

h~o

(6.3.6)

This

is

often called the consistency condition for method (6.3.1). The speed of

convergence of the solution {

Yn}

to the true solution

Y(x)

is related to the speed

of

convergence in (6.3.6), and thus

we

need to know the conditions under which

(6.3.7)

for some desired choice of

m

~

1.

We now examine the implications of (6.3.6)

and (6.3.7) for the coefficients in (6.3.1). The convergence result for (6.3.1)

is

given later as Theorem

6.6.

Theorem 6.5 Let m

~

1 be a given integer. In order that (6.3.6) hold for all

continuously differentiable functions

Y(x),

that

is,

that the method

(6.3.1) be consistent, it

is

necessary and sufficient that

p p

-

'L

jaj

+

'L

bj

==

1

(6.3.8)

j=O

j=

-1

And for (6.3.7)

to

be valid for all functions

Y(x)

that are m + 1

times continuously differentiable, it is necessary and sufficient that

(6.3.8) hold and

that

p p

"'

( .)i + .

"'

(

.)i-lb

1

.t...

-1

aj

z

.t...

-J

j =

i = 2,

...

, m (6.3.9)

j=O

j=

-1

Proof Note that

(6.3.10)

for all constants

a,

f3

and all differentiable functions

Y,

W.

To examine

the consequences of (6.3.6) and (6.3.7) expand

Y(x)

about xn, using

Taylor's theorem 1.4, to obtain

m 1 .

Y(x) = L

;-(x-

xJ'y(i>(xJ

+

Rm+

1

(x)

i=O

l.

(6.3.11)

assuming

Y(x)

is m + 1 times continuously differentiable. Substituting

into (6.3.4) and using (6.3.10),

--

-~--·--

·-·

__________

j

MULTISTEP METHODS 359

Fori=

0,

Fori~

1,

This gives

p

Tn(l) = c

0

= 1 - L

aj

j=O

i

~

1

If

we write the remainder

Rm+

1

(x)

as

1

Rm+l(x)

=

(x-

X

)m+ly(m+ll(x

) + · · ·

(m

+ 1)! n n

then

(6.3.12)

(6.3.13)

{6.3.14)

c

T

(R

) =

--

~hm+ly(m+ll(x

) + O(hm+

1

)

{6

3 15)

n

m+l

(m

+

1

)!

. n • •

assuming Y

is

m + 2 times differentiable.

To

obtain the consistency condition (6.3.6),

we

need

r(h)

=

O(h),

and this requires Tn(Y) = O(h

1

).

Using (6.3.14) with m = 1,

we

must

have

c

0

,

c

1

=

0,

which gives the set of equations (6.3.8). In some texts,

these equations are referred to as the consistency conditions. To obtain

(6.3.7) for some m

~

1,

we

must have Tn(Y) =

O(h"'+

1

).

From (6.3.14)

and (6.3.13), this will be true if and only if

c;

=

0,

i =

0,

1,

...

, m. This

proves the conditions

(6.3.9) and completes the proof. •

The largest value of m for which (6.3.7) holds is called the order or order

of

convergence of the method (6.3.1). In Section 6.7,

we

examine the deriving of

methods of any desired order.

We now give a convergence result for the solution of

(6.3.1). Although the

theorem will not include all the multistep methods that are convergent, it does

include most methods of current interest. 'Moreover, the proof is much easier

than that of the more general Theorem

6.8 of Section 6.8.

!

I

__

j

360 NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS

Theorem 6.6 Consider solving the initial value problem

-y'=f(x,y)

using the multistep method (6.3.1). Let the initial errors satisfy

71(h)

=

Max

IY(x;)-

Yh(x;)

I-+

0

Osisp

as h--+ 0 (6.3.16)

Assume the method

is

consistent, that is,

it

satisfies (6.3.6). And

finally,

assume that the coefficients a j are all nonnegative,

j=0,1,

...

,p

(6.3.17)

Then the method (6.3.1)

is

convergent, and

Max I

Y(x,)

- y

11

(x,)

I ::5 c

1

T](/z)

+

C2T(/l)

(6.3.18)

.\1J:=.r,sh

for suitable constants c

1

,

c

2

•

If

the method (6.3.1)

is

of

order

m,

and if the initial errors satisfy 1/(h) =

O(hm),

then the speed of

convergence of the method

is

O(hm).

Proof Rewrite (6.3.4) and use

Y'(x)

=

f(x,

Y(x))

to get

p p

Y(x,+l)

= L

ajY(x,_)

+ h L

bjf(x,_j,

Y(x,_))

+ hT,(Y)

j-0

j-

-1

Subtracting (6.3.1), and using the notation

e;

=

Y(x;)

- Y;.

p p

e,+

1

= L

ajen-j

+ h L

bj[J(x,_j,

Y,_j)

j-0

j-

-1

Apply the Lipschitz condition and the assumption (6.3.17) to obtain

p p

le,+d

::;;

L ajlen-jl + hK L

!bjlle,_jl

+ hT(h)

j-0

j-

-1

Introduce the following error bounding function,

n =

0,

1,

...

, N(h)

Using this function,

p p

len+d

::;;

L

aJ,

+

hK

L lb)fn+l +

h-r(h)

j-0

j-

-1

Atkinson K. An Introduction to Numerical Analysis

Подождите немного. Документ загружается.