Barber J.R. Intermediate Mechanics of Materials
Подождите немного. Документ загружается.

5.7 Unloading, springback and residual stress 265
This reduction in curvature is known as ‘springback’. The final radius of curvature
R
u
on complete unloading can be determined as
1
R
u
=
1
R
max
−
1
R
∗
=
S
Y
Ed
−
M
max
EI
, (5.36)
where (1/R)
max
is the curvature at the maximum bending moment M
max
.
Example 5. 9
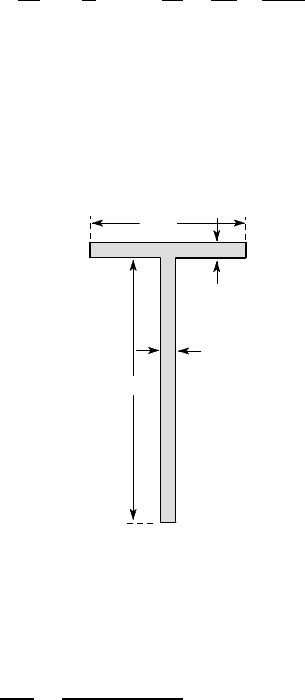
The T-beam of Figure 5.26 is made of an aluminium alloy with E = 80 GPa and
S
Y
= 200 MPa. It is bent to a radius of 10 m and then released. Find the final radius
of curvature and the residual stress distribution.
10
10
170
100
all dimensions in mm
Figure 5.26
We must first determine the applied moment M
max
and the corresponding stress
distribution. From equation (5.15), we have
d =
S
Y
R
E
=
200 ×10
6
×10
80 ×10
9
= 0.025 m = 25 mm.
The location of the neutral axis is determined by the condition that the axial force
F =0. However, since d is considerably less than the total depth of the section, it is
likely that there is an upper plastic zone and that it extends down into the web as
shown in Figure 5.27 (a). In this case, the stress distribution will be as shown in
Figure 5.27 (b), where c is an unknown dimension to be determined. The condition
F = 0 then requires that
(0.1 ×0.01 + c ×0.01)S
Y
−([0.17 −0.05 −c] ×0.01)S
Y
= 0 ,
since the elastic region makes self-cancelling contributions to the axial force. Solving
for c, we have
c = 0.01 m.
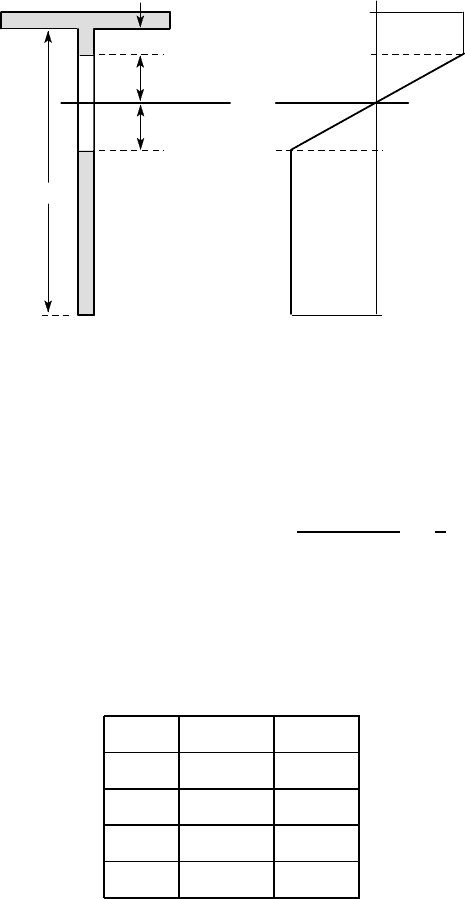
266 5 Non-linear and Elastic-Plastic Bending
170
neutral
axis
d
d
c
A
B
C
D
A
B
C
D
S
Y
-S
Y
(a) (b)
Figure 5.27
The corresponding bending moment is
M
max
= S
Y
(0.1 ×0.01 ×0.04 + 0.01 ×0.01 ×0.03)
−S
Y
(0.11 ×0.01 ×(−0.08)) + 2S
Y
0.01 ×0.025
2
2
3
×0.025
= 200 ×10
6
×13.517 ×10
−3
= 27,033 Nm.
For the unloading problem, we require the location of the centroid and the second
moment of area I
x
. Using the method of §4.3 and treating the web and the flange as
areas A
1
,A
2
respectively, we can construct the first three rows of Table 5.1 (in mm).
Distances are measured from the bottom of the section.
i 1 2
A
i
1700 1000
¯y
i
85 175
I
i
x
4.09 ×10
6
8.3 ×10
3
( ¯y
i
− ¯y) −33.3 56.7
Table 5.1
Thus, the total area is
A = 1700 + 1000 = 2700 mm
2
and the location of the centroid is defined by
5.7 Unloading, springback and residual stress 267
A ¯y = 1700 ×85 + 1000 ×175 ,
giving
¯y = 118.3 mm.
This permits us to complete the last row of the table, after which we obtain
I
x
= 4.09 ×10
6
+ 8.3 ×10
3
+ 1700 ×33.3
2
+ 1000 ×56.7
2
= 9.202 ×10
6
mm
4
= 9.202 ×10
−6
m
4
.
The residual curvature is therefore given by (5.36) as
1
R
u
=
1
10
−
27033
80 ×10
9
×9.202 ×10
−6
m
−1
from which
R
u
= 15.8 m.
Notice that this represents a substantial springback from the radius of 10 m at M
max
.
The final stress distribution is obtained by subtracting the distribution
σ
zz
=
M
max
y
I
=
27033y
9.202 ×10
−6
= 2938y MPa
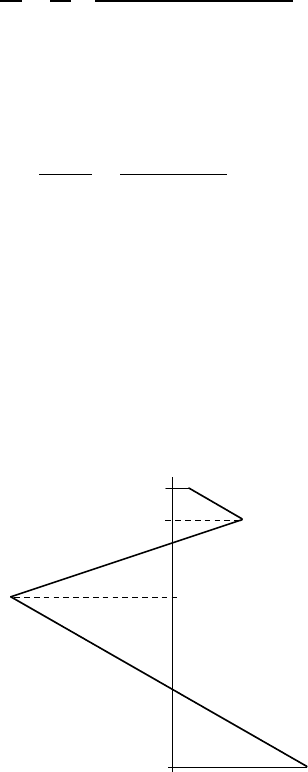
(y in mm) from the distribution of Figure 5.27 (b), noting however that y is mea-
sured from the elastic neutral axis. This gives the piecewise linear stress distribution
sketched in Figure 5.28, which is completely determined by the stresses at the points
A,B,C,D, in Figure 5.27 (a), which are
σ
A
= 200 −2938(0.18 −0.1183) = 18.7 MPa
σ
B
= 200 −2938(0.16 −0.1183) = 77.5 MPa
σ
C
= −200 −2938(0.11 −0.1183) = −175.6 MPa
σ
D
= −200 −2938(−0.1183) = 148 MPa.
A
B
C
D
148
-175.6
77.5
18.7
Figure 5.28

268 5 Non-linear and Elastic-Plastic Bending
5.7.2 Reloading and shakedown
The results of the last section show that a beam that is plastically deformed and then
unloaded will generally exhibit a state of residual stress opposite to that experienced
at the most extreme loading condition. This residual stress is beneficial if the beam is
subsequently loaded again in the same direction. Indeed, since the unloading process
is completely elastic, it is clear that we could reload the beam to within an arbitrarily
small value below the initial maximum moment M
max
without producing any addi-
tional plastic deformation. Perhaps more important from an engineering perspective
is the fact that loading the deformed beam between zero and a moment lower than
M
max
will result in maximum stresses lower than those that would be experienced
by a beam without residual stresses. This means that the fatigue resistance of a beam
subjected to zero to maximum loading can be enhanced by applying an initial over-
load in the direction of the maximum loading, sufficient to produce some plastic
deformation. In effect, the residual stress induced shifts the mean value of the cyclic
stresses closer to zero, without affecting the alternating component.
If the bending moment in a beam oscillates from zero to a maximum value in the
range M
Y
< M < M
P
, plastic deformation will occur during the first loading cycle,
but in subsequent cycles it will just reach the yield limit but not surpass it and no
subsequent plastic deformation will occur. This is a common phenomenon in elastic-
plastic structures subjected to cyclic loading and is known as shakedown. In effect,
the structure tends to deform plastically early in the process in such a way as to
develop a state of residual stress that discourages further plastic deformation. Indeed,
there is a theorem, known as Melan’s theorem
4
, which proves that if any state of
residual stress can be found that would be sufficient to inhibit plastic deformation
during cyclic loading, the structure will in fact shake down until the behaviour is
purely elastic. It is almost as though the structure would do its utmost to avoid its
being subjected to repeated plastic deformation!
It is clear, however, that if the beam is plastically deformed under a bending
moment M and is then subjected to a bending moment of opposite sign, the residual
stress from the first loading will increase the tendency for plastic deformation, so
that a smaller moment is needed to cause first yield in the reverse direction. In most
cases, if a beam is plastically deformed by a bending moment M
1
, (M
Y
< M
1
< M
P
),
elastic deformation will persist on reversed loading as long as
M
1
−2M
Y
< M < M
1
. (5.37)
In other words, the range of bending moments under which the defomation is purely
elastic is equal to 2M
Y
as it would be for a beam without residual stress (−M
Y
<
M < M
Y
), but the mean value is shifted in the direction of the original moment M
1
.
Equation (5.37) may overstate the elastic range under initial unloading if the beam
is unsymmetric and M
1
is close to the fully plastic moment, but under cyclic loading
the system will still shake down eventually as long as (5.37) is satisfied.
4
P.S.Symonds (1951), Shakedown in continuous media, ASME Journal of Applied Mechan-
ics, Vol.18, pp.85–89.
5.8 Limit analysis in the design of beams 269
5.8 Limit analysis in the design of beams
We have seen in §§ 5.4–5.6 that the fully plastic moment M
P
is generally easier to
calculate than M
Y
and exceeds M
Y
by a fairly modest percentage. Since all design
calculations are subject to safety factors to allow for unforeseen overloads and other
uncertainties, an alternative procedure is therefore to perform a fully plastic ‘col-
lapse’ or ‘limit’ analysis of the problem and apply a somewhat larger safety factor.
5.8.1 Plastic hinges
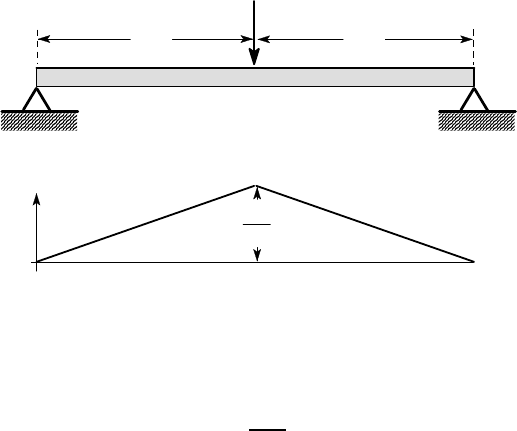
Figure 5.29 shows a simply supported beam with a central load and the correspond-
ing bending moment diagram.
F
A
B
C
A
B
C
FL
4
M
L /
2
L /
2
Figure 5.29: A simply supported beam with a central load
Failure will occur when the maximum bending moment FL/4 reaches M
P
and
hence
F =
4M
P
L
.
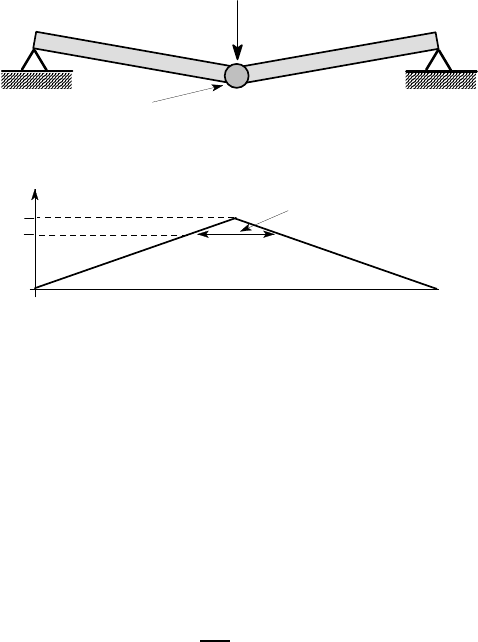
Once this happens, unlimited bending of the beam will occur at B without further
increase in F and the beam will collapse as shown in Figure 5.30 (a).
Some plastic deformation will occur at all points where M > M
Y
and this defines
a range of points around B as shown in Figure 5.30 (b). However, for most beam sec-
tions, the greater part of the deformation is concentrated near B as in Figure 5.30 (a)
and the beam behaves as though it had a sticky hinge at B which requires a moment
M
P
to move it. We describe this process by saying that the beam develops a plastic
hinge at B. Once the hinge is developed, the beam becomes a mechanism in the sense
that unlimited further deformation can occur at the hinge without further increase in
force or additional deformation elsewhere in the beam.
270 5 Non-linear and Elastic-Plastic Bending
F
plastic hinge
A
B
C
A
B
C
M
plastic deformation
range
M
Y
M
P
(a)
(b)
Figure 5.30: (a) Mode of plastic collapse for the simply supported beam, (b) the
corresponding bending moment diagram
5.8.2 Indeterminate problems
For indeterminate problems, collapse requires that the beam or structure develop
enough plastic hinges to remove the redundancy and convert the structure to a mech-
anism. It is usually fairly easy to determine where these hinges must occur. A good
method is to sketch the probable shape of the shear force and/or bending moment
diagrams. Remember that
dM
dz
= V , (5.38)
where V is the shear force, so the maximum and minimum values of bending moment
correspond to points where the shear force passes through zero. In particular, no
plastic hinge can develop in the middle of a beam segment with no lateral load, since
the shear force there must be constant.
Once a probable arrangement of plastic hinges is identified, the problem is re-
duced to one which can be solved using equilibrium considerations alone. This is
almost always a great deal easier than the solution of the corresponding elastic inde-
terminate problem — for example using Castigliano’s Second Theorem (§3.10).
Example 5. 10
The built-in beam of Figure 5.31 (a) is loaded by a uniformly distributed load w per
metre. The beam is made of steel with S
Y
=300 MPa and its cross section is as shown
in Figure 5.31 (b). Find the value of w at plastic collapse.
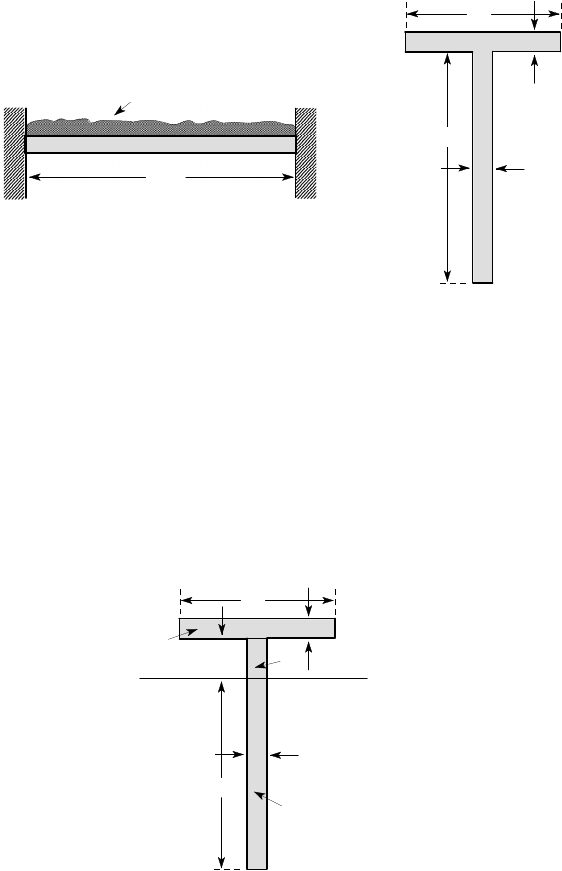
5.8 Limit analysis in the design of beams 271
10
10
120
80
all dimensions in mm
(a) (b)
Figure 5.31
We first need to determine the fully plastic moment M
P
. The total area of the
section is
A = 80 ×10 + 120 ×10 = 2000 mm
2
,
so the median line cuts the section at a distance 100 mm (1000 mm
2
/10 mm) from
the bottom of the section as shown in Figure 5.32.
10
10
80
neutral
axis
20
100
1
A
A
3
A
2
all dimensions in mm
Figure 5.32
Taking moments about the bottom of the section, the fully plastic moment is then
determined as
M
P
= 300 ×10
6
(0.08 ×0.01 ×0.125 + 0.02 ×0.01 ×0.11 −0.1 ×0.01 ×0.05)
= 21600 Nm.
8 m
w per metre
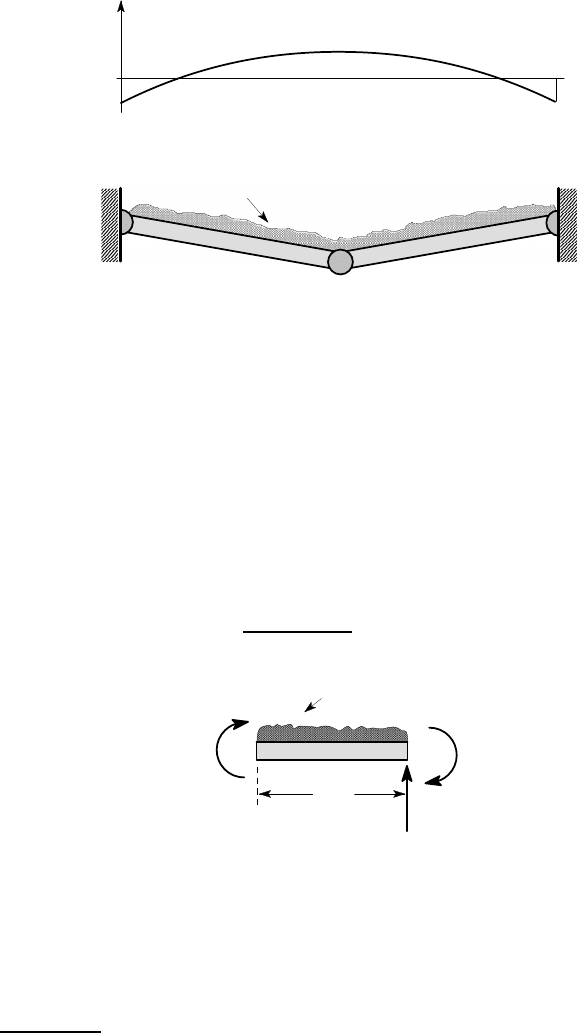
272 5 Non-linear and Elastic-Plastic Bending
A
B
C
M
(a)
Figure 5.33
The bending moment diagram will be as shown in Figure 5.33 (a), so first yield
will occur either at the supports or at the mid-point. However, the development of a
single plastic hinge is not sufficient to cause the beam to collapse. The load can be
increased further until the beam is converted to a mechanism by the establishment of
plastic hinges at all three points ABC as shown in Figure 5.33 (b). Taking moments
about C in the free-body diagram
5
for the segment BC (Figure 5.34) then yields the
equilibrium equation
2M
P
−4w ×2 = 0
and hence
w =
2M
P
(4 m ×2 m )
= 5400 N/m.
w per metre
Figure 5.34
5.9 Summary
In this chapter, we have developed methods for determining the stress distribution
and the curvature for beams that are loaded into the plastic range. The same methods
can also be used for non-linear elastic materials. The strain is always a linear function
5
Notice that the moments M
P
must oppose the relative rotations in Figure 5.33 (b).
(b)
A
B
C
w per metre
4 m
4 w
M
P
M
P
B
C
5.9 Summary 273
of position in the section and the three constants describing this deformation can in
principle always be found from three equilibrium equations defining the transmitted
force and moments.
If a beam is bent about an axis of symmetry, this will also be the neutral axis if
there is no axial force. Symmetric regions yielded in tension and compression are
separated by an elastic region. If the moment axis is not an axis of symmetry, the
neutral axis generally moves as plastic deformation progresses.
The maximum bending moment (the fully plastic moment) corresponds to the
situation where the elastic zone has shrunk to zero and the beam then develops a
plastic hinge. For a rectangular beam section, the shape factor f = 1.5, meaning that
the load can be increased by 50% beyond first yield before collapse occurs. This
‘residual strength’ for an elastic-beam is a useful reserve in design to accommodate
unlikely extreme loading events. However, more ‘efficient’ sections such as I-beams
have values of f much closer to unity, since most of the section area is concentrated
at the same distance from the neutral axis. In such cases, a good design strategy is to
calculate the fully plastic moment and use an appropriate safety factor. This method
is particularly useful in designing complex indeterminate structures for strength.
If a beam is loaded into the plastic range and then unloaded, it will be left in a
self-equilibrated state of residual stress and will have some residual curvature. This
is important in forming operations involving bending, since the elastic recovery or
‘springback’ must be allowed for in designing appropriate forms and tools. Also, the
tensile residual stresses may influence the fatigue life of formed components.
Further reading
Elastic-perfectly plastic stress distributions
W.F. Riley and W. Zachary (1989), Introduction to Mechanics of Materials, Wiley,
New York, NY, Chapter 10.
Nonlinear constitutive laws
J.M. Gere and S.P. Timoshenko (1997), Mechanics of Materials, PWS Publishing
Company, Boston, MA, 4th edn., §6.10.
Limit analysis
E.P. Popov (1998), Engineering Mechanics of Solids Prentice Hall, Upper Saddle
River, NJ, 2nd edn., Chapter 20.
I.H. Shames and F.A. Cozzarelli (1992), Elastic and Inelastic Stress Analysis, Pren-
tice Hall, Engelwood Cliffs, NJ, Chapter 10.
W.F. Riley and W. Zachary (1989), loc. cit.
274 5 Non-linear and Elastic-Plastic Bending
Problems
Section 5.4
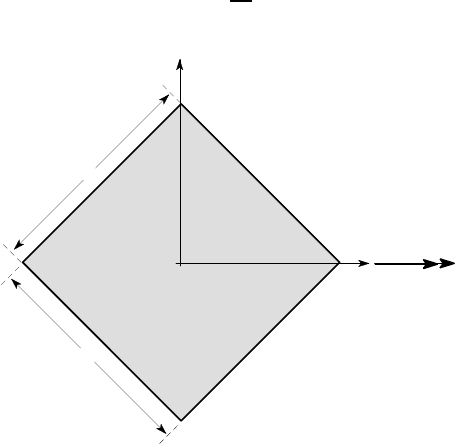
5.1. A beam of square cross section a×a is bent about a diagonal axis by a moment
M, as shown in Figure P5.1. Find the relation between M and the radius of curvature
R, if the material obeys the constitutive law
σ
zz
= E
e
zz
+
e
3
zz
e
2
0
.
M
a
a
y
O
x
Figure P5.1
5.2. A certain polymer fails in tension at a stress
σ
0
and its uniaxial constitutive law
is approximated by the equation
σ
zz
= 0.6
σ
0
e
0.2
zz
; e
zz
> 0
= −0.6
σ
0
|e
zz
|
0.2
; e
zz
< 0 .
It is used for a rectangular beam of width b and height h. Find the maximum bending
moment that can be transmitted by the beam without failure.
5.3. Find the fully plastic moment M
P
for the I-beam shown in Figure P5.3, if the
uniaxial yield stress of the material is S
Y
=100 MPa.
At what percentage of the fully plastic moment will the flanges of the beam be
fully plastic, whilst the web remains elastic?
