Barber J.R. Intermediate Mechanics of Materials

Подождите немного. Документ загружается.

6.1 Derivation of the shear stress formula 295

In general, if the section crosses the neutral axis only once, the stress there will be

in the same direction as V

and the shear ﬂow will continue along the section, dimin-

ishing in magnitude towards the extremities of the section. At all points it remains

locally parallel to the wall of the section.

Example 6. 1

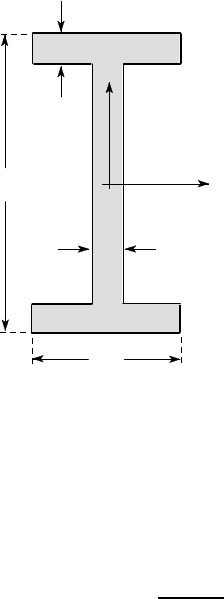
The I-beam of Figure 6.11 is loaded by a vertical shear force of 50 kN. The ap-

propriate centroidal second moment of area for the section is I

= 39.4 ×10

Find

(i) the complete distribution of shear stress in the section,

(ii) the maximum shear stress,

(iii) the average vertical shear stress,

(iv) the proportion of the shear force that is carried by the web,

(v) the average shear stress in the web.

200

100

all dimensions in mm

Figure 6.11

(i) To determine the complete shear stress distribution, we need to make two cuts at

arbitrary points — one in the web and one in the ﬂange as deﬁned in Figure 6.12.

For the web, we use the cut BC of Figure 6.12 (a), obtaining

∗

¯y

∗

= A

¯y

+ A

¯y

= (80 −y) ×20 ×

(80 + y)

+ 100 ×20 ×90

= 244, 000 −20y

(y in mm)

and hence

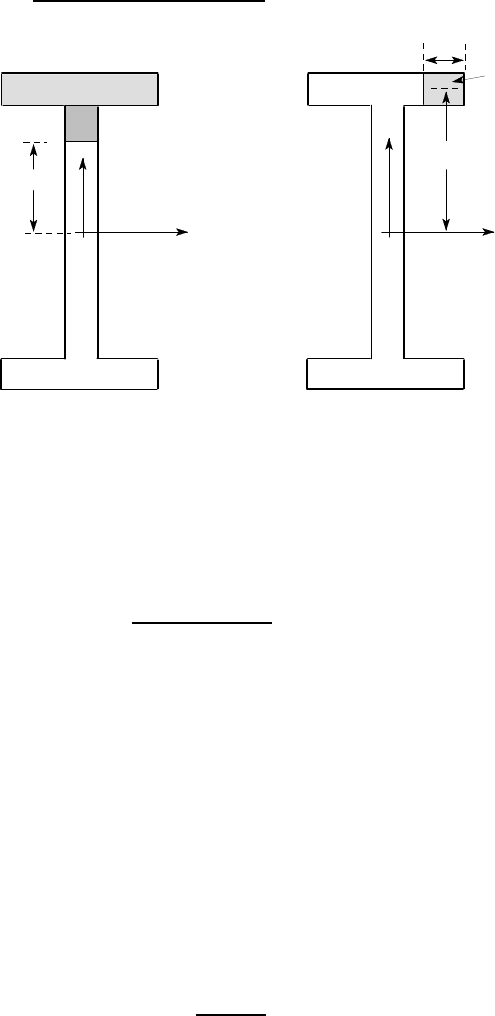
296 6 Shear and Torsion of Thin-walled Beams

50 ×10

×(244,000 −20y

)

39.4 ×10

×20

= 15.5 −1.27 ×10

−3

MPa .

(a) (b)

Figure 6.12: (a) cut BC, (b) cut DE.

For the ﬂange, we use the cut DE of Figure 6.12 (b), obtaining

∗

¯y

∗

= x ×20 ×90 = 1800x mm

(x in mm)

and hence

50 ×10

×1800x

39.4 ×10

×20

= 0.1142x MPa .

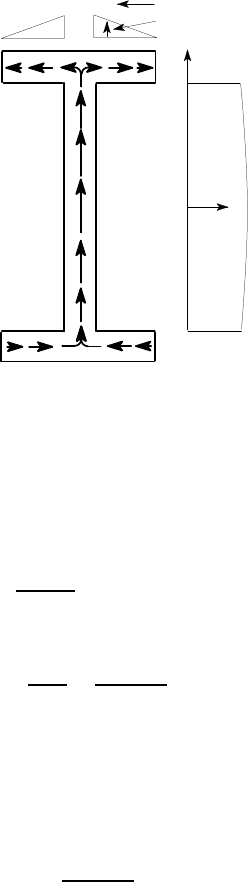
Thus, the shear stress varies linearly in the ﬂanges and quadratically in the web, as

shown in Figure 6.13.

(ii) Since t is the same at all sections, the maximum shear stress occurs in the web at

the neutral axis (y = 0), where A

∗

¯y

∗

is maximum. We obtain

max

= 15.5 MPa .

(iii) The average vertical shear stress is simply the shear force divided by the total

area of the section which is

A = 2 ×100 ×20 + 160 ×20 = 7200 mm

Hence

ave

50 ×10

7200

= 6.9 MPa .

6.1 Derivation of the shear stress formula 297

flange

web

Figure 6.13: Shear stress distribution in the I-beam

(iv) The total shear force carried in the web can be obtained by summing (integrating)

the shear stress over the web. We obtain

F =

−80

(15.5 −1.27 ×10

−3

)20dy = 49,167 N (49 kN) .

Thus the proportion of the shear force carried by the web is

49,167

50,000

= 0.983 (98.3%) .

(v) The average shear stress in the web is

web

ave

web

49167

160 ×20

= 15.4 MPa .

Notice, from (iv) above, that almost all the vertical shear force is carried by the

web. Also, there is only a modest variation in shear stress over the web. Even at the

top of the web, where y = 80 mm, the shear stress is 11.4 MPa, from (i) above with

y=80 mm. For this reason, a reasonable estimate of the maximum shear stress in the

I-beam can be obtained very quickly by just dividing the shear force by the web area

— i.e.

max

≈

50,000

160 ×20

= 15.6 MPa ,

which is a very good quick approximation to the correct value obtained in (ii) above.

6.1.2 Location and magnitude of the maximum shear stress

In equation (6.9), only A

∗

, ¯y

∗

and t vary with position in the section and hence the

maximum transverse shear stress occurs at the point where the ratio A

∗

¯y

∗

/t is a max-

imum. Elemental areas dA make a positive contribution to

298 6 Shear and Torsion of Thin-walled Beams

∗

¯y

∗

ydA

if and only if y > 0 — i.e. if they are above the neutral axis. It follows that the

maximum value of A

∗

¯y

∗

occurs when the cut is made at the neutral axis, in which

case A

∗

comprises that part of the section above the neutral axis. If the thickness t is

constant, as in Example 6.1, the maximum shear stress will therefore always occur

at the neutral axis.

neutral

plane

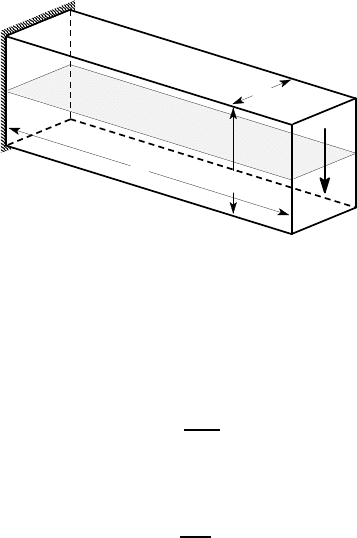
Figure 6.14: Cantilever beam of rectangular cross section

For a beam of rectangular cross section, the transverse shear stresses are always

substantially smaller than the normal stresses due to bending. Consider, for example,

the rectangular cantilever beam of Figure 6.14, loaded by an end force F. Elementary

calculations show that the maximum bending stress occurs along the line AB and is

max

6FL

(6.10)

and the maximum shear stress, calculated from equation (6.9) occurs at the neutral

plane and is

max

2bh

. (6.11)

Thus,

max

will exceed

max

if and only if L<h/4 — i.e. if the beam is only a quarter

as long as its height, which takes the problem well outside the range of application

of beam theory, for which we require L ≫h,b.

Larger transverse shear stresses will be obtained if the section has a locally re-

duced thickness t, particularly if this occurs at or near to the neutral axis, as shown in

Figure 6.15. However, it is still comparatively rare to encounter an application where

the shear stresses due to shear loading are comparable with those due to bending. For

this reason, it is frequently appropriate in design to neglect shear stresses altogether,

or else to use a crude approximation for them such as

≈V

/A or

≈V

web

. In

Example 6.1, these approximations gave at least an order of magnitude estimate of

the maximum shear stress and could therefore have been used to determine whether

this magnitude was sufﬁciently high to justify the effort involved in a more exact

calculation.

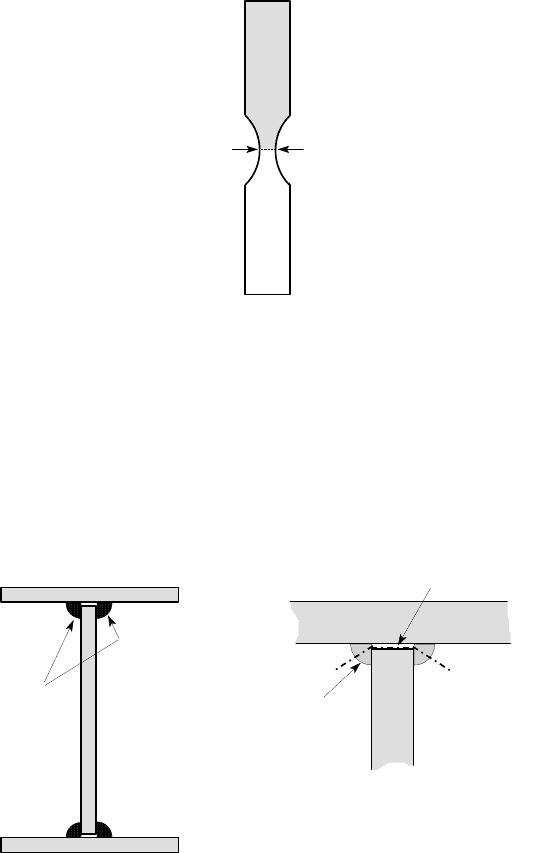
6.1 Derivation of the shear stress formula 299

Figure 6.15: Beam with a reduced thickness at the neutral axis

6.1.3 Welds, rivets and bolts

There are not many applications where we would need to use a beam with a locally

reduced thickness t, but a similar effect is produced when a beam is fabricated by

welding three plates together as shown in Figure 6.16 (a). In this case, the thickness

at the weld may be smaller than that of the rest of the section. Also, the stresses in

the weld are of particular interest, since the weld material may contain defects and

hence be weaker than the rest of the material.

welds

air gap

cut

weld

(a) (b)

Figure 6.16: A beam fabricated from three rectangular plates

To determine the maximum shear stress in the weld, we make the shortest cut

that would be sufﬁcient to cause the ﬂange to drop off, since the cut must separate

the section into two parts in view of the argument of §6.1. This can be achieved by

cutting through both welds as shown in Figure 6.16 (b).

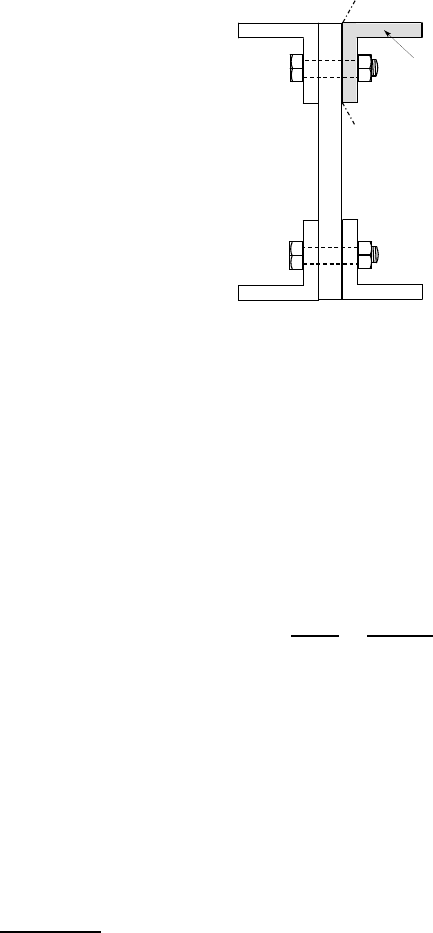
300 6 Shear and Torsion of Thin-walled Beams

Notice that the cut doesn’t even have to be a plane or to be connected. The thick-

ness t is the total length along the cut line, not including air. Here we would get twice

the smallest thickness through the weld.

cut

Figure 6.17: A beam assembled with bolts

A similar technique can be used if rivets or bolts are used to attach the ﬂange

instead of welds, as shown in Figure 6.17. This time, we imagine cutting through

the bolts to make one angle drop off. However, we cannot deﬁne a thickness t here,

since the angle is joined to the rest of the section by a set of discrete areas. Instead,

we must go back to the concept of shear ﬂow q, which is the horizontal shear force

per unit length transmitted through the bolts. This must be transmitted through the

total bolt cross-sectional area per unit length, which in turn is the cross-sectional area

of one bolt multiplied by the number of bolts N per unit length. If the bolts are of

diameter d, we have a shear area of

/4 per unit length and the average shear

stress in the bolts is therefore

bolts

∗

¯y

∗

, (6.12)

where we note that A

∗

and ¯y

∗

relate to the section that would be removed by the cut,

as in more conventional problems.

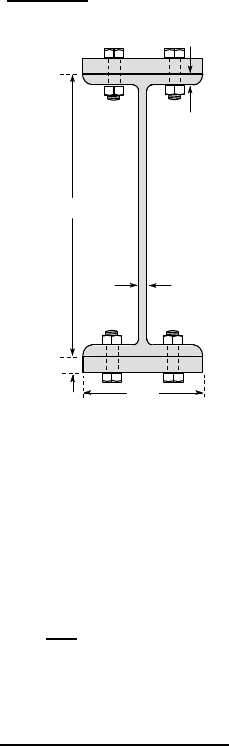
Example 6. 2

Figure 6.18 shows a W610×101 I-beam that has been stiffened against bending by

the attachment of two 230×25 mm rectangular plates. The plates are secured to the I-

beam by 10 mm diameter bolts with an axial spacing of 100 mm. The second moment

of area of the I-beam without the stiffeners is 764×10

. Find the average shear

stress in the bolts if the beam transmits a shear force of 50 kN.

In calculating the shear stress for this cut using equation (6.9), we can neglect the small

contribution to A

∗

¯y

∗

from the fragments of weld adhering to the section removed.

6.1 Derivation of the shear stress formula 301

We ﬁrst calculate the second moment of area I

for the stiffened section, using

the parallel axis theorem, with the result

= 764 ×10

+ 2



230 ×25

+ 230 ×25 ×314



= 1898 ×10

14.9

603

230

10.5

Figure 6.18

If we cut through the top ﬂange bolts, the area cut off (A

∗

) is 230×25 and

∗

¯y

∗

= 230 ×25 ×314 = 1.806 ×10

The axial bolt spacing is 100 mm and there are two bolts at each axial location,

so the number of bolts per unit length is

N =

100

= 0.02 bolts per mm .

Substituting these results into equation (6.12), we obtain

bolts

4 ×50, 000 ×1.806 ×10

×10

×0.02 ×1898 ×10

= 30 MPa .

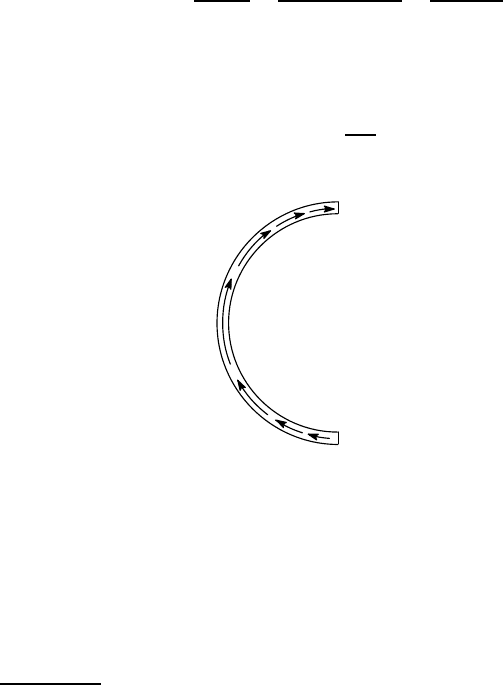
6.1.4 Curved sections

If a thin-walled beam contains curved sections, the procedure for determining the

transverse shear stress is the same, but integration will generally be needed in deter-

mining I

and A

∗

¯y

∗

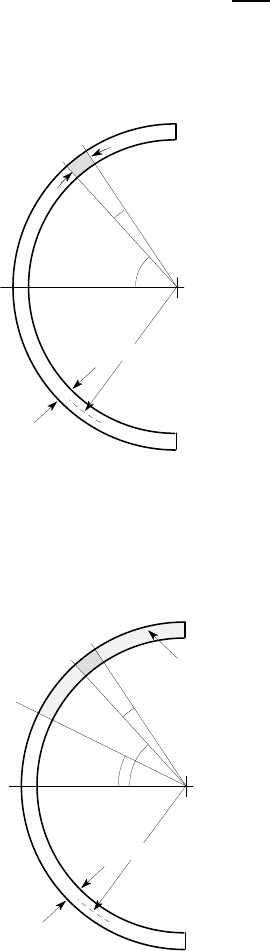
. We illustrate this with the example of the semicircular section of

Figure 6.19, with radius a and thickness t, where t ≪a.

To determine I

, we consider a small element dA =atd

shown shaded in Figure

6.19. Then

302 6 Shear and Torsion of Thin-walled Beams

dA =

−

(asin

)

atd

= a

−

sin

. (6.13)

Notice that I

is a property of the whole section, so the integral is performed over the

entire semi-circle from end to end.

dθ

adθ

Figure 6.19: Thin-walled semi-circular cross section

We now make a cut at a general point

to determine the shear stress, as

shown in Figure 6.20.

dθ

cut

Figure 6.20: Cut for determining the shear stress in the semi-circular section

6.2 Shear centre 303

The quantity A

∗

¯y

∗

relates only to the section cut off, which is deﬁned by

/2. These are therefore the limits of integration.

We obtain

∗

¯y

∗

ydA =

(asin

)atd

= a

t cos

. (6.14)

It is important to ensure that the limits of integration correspond to the edges of the

area A

∗

and that the lower limit is smaller than the upper limit.

The shear stress at the point

∗

¯y

∗

×(a

t cos

)

(

t/2) ×t

cos

. (6.15)

We see from equation (6.15) that the shear stress varies sinusoidally around the

section from zero at the ends (

= ±

/2) to a maximum at the neutral axis (

= 0),

given by

max

. (6.16)

It is parallel to the section wall at all points, as shown in Figure 6.21.

Figure 6.21: Shear stress distribution for the semi-circular section

6.2 Shear centre

The theory presented above gives a unique solution for the shear stress throughout the

section for a given value of V

. This implies that the line of action of V

is prescribed,

since the distribution of

over the section has a resultant in magnitude, direction and

line of action.

Notice that it is necessary to deﬁne two indeﬁnite angles

in order to calculate the stress

at a general point. One of these angles (

) deﬁnes the point under consideration and the

other (

) serves as a variable of integration in the summation for A

∗

¯y

∗

. A common error

is to use only one such variable and then use deﬁnite limits in the integration. At best, this

will only yield the stress at a particular point.

304 6 Shear and Torsion of Thin-walled Beams

If the actual shear force applied has a different line of action from that implied

by the theoretical distribution, there will be some twisting of the section and a more

complex shear stress distribution will be developed.

There is a unique point C for any given beam section, such that if the line of

action of V passes through C, the section does not twist. This point is called the

shear centre. For a doubly-symmetric section, like an I-beam, the shear centre will

coincide with the intersection between the two axes of symmetry. For sections with

one axis of symmetry, the shear centre lies on that axis, but it’s location must be

found by determining the line of action of the shear force implied by the distribution

of shear stress from the preceding analysis.

6.2.1 Finding the shear centre

To ﬁnd the shear centre of a thin-walled section, we must determine the line of action

of the resultant force due to the shear stress distribution

of equation (6.9). The shear

stress is everywhere locally parallel to the thin wall and it generates an elemental

force dF =

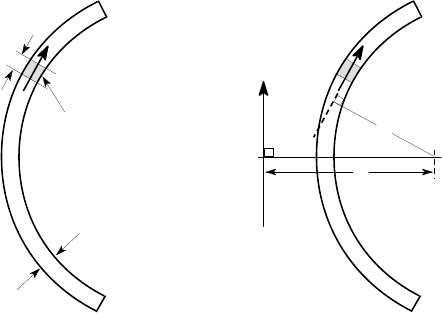
dA on the elemental area dA shown in Figure 6.22 (a). We can write

dA=tdS, where dS is an element of the perimeter and hence

dF =

tdS = qdS . (6.17)

(a) (b)

Figure 6.22: (a) The elemental force dF, (b) deﬁnition of the dimensions c and n

The shear force V

is the resultant of the elemental forces dF and it must therefore

have the same moment about any point O. We conclude that

c =

ndF =

tdS =

nqdS , (6.18)

where the integration is performed over the entire perimeter of the section, c deﬁnes

the location of the shear centre and n is the moment arm for the elemental force dF,

i.e. the perpendicular distance from O to the line of action of dF (the local tangent

to the mean line of the section), as shown in Figure 6.22 (b).