Barnes D.J., Chu D. Introduction to Modeling for Biosciences
Подождите немного. Документ загружается.


3.4 Malaria Model in Repast Using Java 123
Fig. 3.13 Scatter plots of human and mosquito infection levels
plotted and what information is required from the chart. We will use a basic scatter
plot to visualize how the infection numbers vary over time.
The chart can be given a name, and the data set it is based on must be selected.
A drop-down list of mappings allows the data for the x-axis to be selected and
the Add button adds other mappings to be plotted on the y-axis. Note that if there
are more than two mappings in the data set then these can be plotted on the same
chart.
The Visual Settings dialog is where the type of chart is selected, and the behavior
of the axes; for instance, whether these have a fixed range or vary according to the
data. We will select a scatter plot and use an auto range for the y-axis but not the
x-axis. We create separate charts for human and mosquito infection levels because
it is not possible to mix the data from different data sets in the same chart. Running
the model results in the two charts being updated continuously, with the x-axis range
increasing at each tick. We can use the floating window control in the chart display
to view both charts together (Fig. 3.13). In Sect. 3.4.13 we will look at a way to
include data about different types of agents on a single chart.

124 3 ABMs Using Repast and Java
3.4.12 Outputting Data
The data plotted on a chart represents the results of a single run of the model, and is
lost at the end of the run. However, by setting up an outputter from the scenario tree,
we can preserve the results both for future investigation and either comparative or
aggregated analysis over multiple runs. We could easily perform that analysis with
a tool such as gnuplot (Chap. 5).
Right-clicking Outputters offers Add File Outputter. The dialog allows the output
to be named and the data set to be selected. The data will be output as a delimited
file. The columns of the data set to be included in the output have to be indicated by
transferring their names from the left column to the right. The next dialog is where
the file properties are specified; in particular, the name of the file and how the output
from different runs is to be distinguished, such as by inserting the time of the run
in the file name. At the end of a run, the output file is listed in the package explorer
of the main Eclipse window. Once again, we note that it is not possible to combine
the output from different data sets in a single output set, but we will address this in
Sect. 3.4.13.
3.4.13 A Statistics-Gathering Agent
In both Sects. 3.4.11 and 3.4.12 we noted that having separate data sets for humans
and mosquitoes effectively enforced separate charting and separate outputting of
that data. This was because data sets are based on agent types, as listed in the score
file. In addition, we note that data gathering involves a separate pass over every
agent, obtaining one or more properties and processing or aggregating those values.
With a large number of agents, this separate pass could add significantly to the
run time of the model, depending upon the relative complexity of the regular agent
actions.
One way to get around these potential limitations is to introduce an artificial
agent into the model, whose role is to gather the required data during the course of
the normal agents’ actions. This extra agent could store information on the different
agent types (thus allowing data on multiple types to be displayed on a single chart or
within a single output file) and only needs to be a singleton instance
13
(potentially
reducing the runtime cost of data gathering at the end of each step).
As the introduction of this new agent, which we will call AgentStatistics,
will require some significant refactoring of the current Repast project, we will ac-
tually make the changes in a copy of the project: MalariaModelVersion2. Unfortu-
nately, it is not possible simply to copy and paste a Repast project in Eclipse via
the package explorer as the copy will still refer to the original project in too many
places. Instead, we create a new Repast project and copy the source files across from
the original project, then create a new score file.
13
A singleton class permits at most one instance of the class to be created.
3.4 Malaria Model in Repast Using Java 125
Although our new singleton agent does not play any part in the interactions
within the model, it still needs to be stored within the root context so that the
data gathering process can interact with it when building a data set. This presents a
slight problem, because the context is currently configured to store only infectable
agents. It would not be appropriate to define AgentStatistics as a subclass
of InfectableAgent because there is no similarity at all between it and the
Human and Mosquito classes. We resolve this in the following way, which is a
general solution for issues of this type:
• We define a new Java interface called Agent that is completely empty: it has no
methods or fields. It acts as the supertype of all agents in the model, in much the
same way as the standard Java class Object acts as the supertype of all classes
in ordinary programs.
• We specify that both AgentStatistics and InfectableAgent imple-
ment this interface. Because the interface is empty, this requires no implementing
code to actually be written in these classes.
• We change the context builder so that it is now parameterized, and builds contexts
of Agents rather than InfectableAgents.
Since humans are infectable agents, which are agents, they can still be added to the
context. There are some knock-on changes in the sources of the existing classes—
primarily to change most of the references to InfectableAgent to be references
to Agent—but these are relatively easy to achieve with source-code refactoring
support from Eclipse.
Code 3.9 shows how the singleton class, AgentStatistics, is defined. The
idea is that the single instance is created directly within the class itself (note that the
class has a private constructor) and the getInstance method is called instead to
access the lone instance. The following is added to the context builder to place the
instance in the root context:
// Store an agent in the main context for gathering statistics.
context.add(AgentStatistics.getInstance());
As can be seen from Code 3.9, it is assumed that there is a static get-
InfectedPercentage method in the Human and Mosquito classes. The idea is
that these classes keep track of the overall infection numbers as the agents go from
healthy to infected and vice versa. This work is shared between InfectableAgent,
Human and Mosquito:
• Human and Mosquito each maintain a static variable containing the number of
objects of that type—this is set by the context builder when it reads the model
parameters.
• Human and Mosquito each maintain a static variable that counts the number of
infected instances.
• Human and Mosquito define two methods: one to increment the infected count
and one to decrement it. These methods are declared as abstract in InfectedAgent.
• When the infect method in InfectedAgent is called, if the agent was previously
healthy then the increment method is called.

126 3 ABMs Using Repast and Java
/**
* Provide access to agent statistics via a singleton instance.
*/
public class AgentStatistics implements Agent
{
// The singleton instance.
private static final AgentStatistics singleton =
new AgentStatistics();
/**
* Create an AgentStatistics object.
* This may only be created locally.
*/
private AgentStatistics()
{
}
/**
* @return The singleton instance.
*/
public static AgentStatistics getInstance()
{
return singleton;
}
/**
* @return The percentage of infected mosquitoes.
*/
public double getMosquitoInfectedPercentage()
{
return Mosquito.getInfectedPercentage();
}
/**
* @return The percentage of infected humans.
*/
public double getHumanInfectedPercentage()
{
return Human.getInfectedPercentage();
}
}
Code 3.9 The singleton AgentStatistics class
• When the setHealthy method in InfectedAgent is called, if the agent was
previously infected then the decrement method is called.
These rules are implemented in the MalariaModelVersion2 project.
With the AgentStatistics class registered as an agent in model.score, it becomes
available when setting up a data set in the scenario tree. We add a data set called
Health statistics and select AgentStatistics as the agent class. We then add
three simple mappings: the tick, getHumanInfectedPercentage and get-
MosquitoInfectedPercentage. When creating a chart we select the tick for
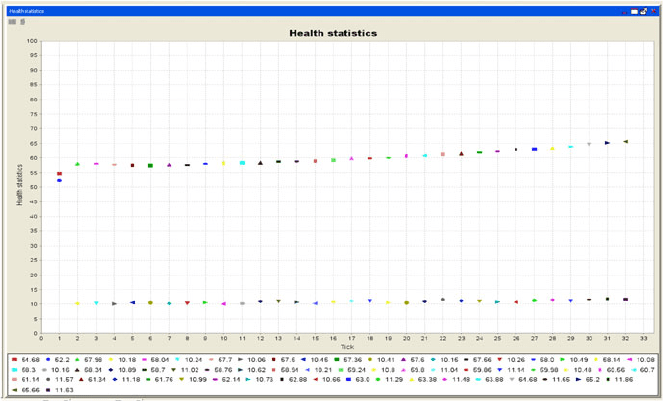
3.4 Malaria Model in Repast Using Java 127
Fig. 3.14 Percentage infection rates for humans and mosquitoes on a single chart
the x-axis and the two percentage columns for the y-axis. We use a scatter with
no auto-range on the x-axis and a fixed range on the y-axis as we are displaying
percentages: a minimum of 0 and a maximum of 100.0. Figure 3.14 illustrates how
this might look for a particular set of parameters. In a similar way, when defining an
outputter, we are able to record both percentages against each tick in a single output
file, because they are all recorded in the same data set.
3.4.14 Summary of Concepts Relating to the Malaria Model
Working with the malaria model offered us the opportunity to explore how to create
a simulation in a way that is much closer to how we might write a program from
scratch in Java. However, in doing so we were still able to take advantage of the
features that Repast offers in the form of a simulation infrastructure—agent orga-
nization and event scheduling—plus the visualization, charting, data storage tools,
and so on. Therefore, nearly all of our programming effort was focused on the model
itself: the agents, their properties, behaviors and interactions. Some additional effort
was required in order to work with the Repast API: context builders, runtime envi-
ronments, parameters, etc., but the cost here is largely of the type associated with
any start-up operation. These features will be used in every model built with Repast.
While it was still necessary to define a score file, we took a different approach
to model initialization—preferring to program that ourselves within the context
builder. This also involved using a projection factory. We made use of the fact that
the score file allows us to parameterize the model for different runs, accessing exter-
nally set values via a Parameters object. We also saw how to differentially prioritize
128 3 ABMs Using Repast and Java
behaviors to ensure correct sequencing within the model. For agent visualization we
looked at how to customize the default style by overriding just a couple of methods
of the DefaultStyle2D class.
3.4.15 Running Repast Models Outside Eclipse
It will often be the case that the results obtained from a single run of a model are not,
themselves, of particular significance. Rather, it is the average behavior observed
over a number of runs that we are interested in. For instance, we might find that
the infection rate among humans at the end of a run is 43.17%, yet averaged over
100 runs it might turn out to be 47.82%; the average value is of more significance
than any single result within those 100 runs. In addition, a full understanding of
a model’s behavior will often only be obtained when it is run multiple times with
varying parameters. For instance, how is the average final infection rate affected by
the density of humans within the model’s space? If we are to answer questions such
as these in an efficient fashion with Repast then we need a way: (i) to run the model
multiple times, and; (ii) to be able to vary the parameters between runs. Running
interactively is not efficient, and editing the model.score file between runs is also
not efficient. Fortunately, Repast provides a way to allow us to run our models in
batch mode.
Running Repast in batch mode means that it does not display its user interface or
the runtime GUI. A special starting point, called BatchMain, has to be executed
rather than Eclipse. This is executed from a command-line window and the exact
details will depend upon the particular operating system, e.g., Windows, Mac or
Linux. See Appendix A.1 for specific details. The basic execution in batch mode
will look something like this:
java -cp classpath repast.batch.BatchMain [ options ] target
The elements that have to be customized are:
• classpath: A list of folders and jar (Java archive) files making up the Repast
program. There may be a large number of these.
• options: Options customizing the batch run. The only one we will consider here
is -params as it allows us to name a file of parameters values to be used during
the run.
• target: The file system path of the Repast scenario (folder containing the file
model.score).
Full details of the variations available for the options and target elements can be
found in the Repast S Reference document.
To illustrate Repast in batch mode, we will use a further variation on the malaria
model, which we will maintain as a separate Repast project called MalariaModel-
Batch. The dynamics of this model are identical to the previous versions; the
changes relate purely to its use in batch mode:

3.4 Malaria Model in Repast Using Java 129
• Rather than using a fixed initial infection rate of 50% for both humans and
mosquitoes, we have added parameter values to the score file to allow the rates to
be individually configured.
• Rather than collecting infection rates at every time tick we are only interested in
the final infection rate for humans, so we have adapted the outputter to reflect
this.
• In addition to the final infection rate, we output the density of humans within
the model. This requires a new method in the AgentStatistics class. Having these
values output together makes it easier to plot the results.
• It is important to bear in mind that, when running in batch mode, any static vari-
ables in the Java code are only initialized right at the beginning of the first run, and
not before every single execution of the model. Where a static variable is being
used to accumulate information during a run (the infectedCount variables in
the agent classes, for instance), it is essential to reset these variables explicitly be-
fore each run. We have added resetInfectedCount methods to the Human
and Mosquito classes, therefore, and call these in the context builder immediately
before creating the agent objects for each run. It is easy to overlook this kind of
thing!
The number of runs and the parameter values for each run are configured
from a file we will call the sweep file. An empty copy of a sweep file, called
batch_params.xml, is included in every Repast project’s file structure within
its batch sub folder:
<?xml version="1.0"?>
<sweep runs="1">
</sweep>
Once the required parameter settings have been added, it is the sweep file that is
named on the command line after the -params option. The contents of the sweep
file are straightforward: each parameter of the particular model is named and the
values the parameter is to take on are listed. The runs attribute at the head of the
file governs how many times the model will be run with the parameters values. This
makes it easy to run the model multiple times with fixed parameters and obtain an
average from the individual runs.
Every parameter of the model must have an entry in the sweep file. Here is an
example of a parameter that will be set to a constant value on every run:
<parameter name="humanInfectionPeriod" type="constant"
constant_type="number" value="40.0" />
For parameters whose values are varied on different runs there are two forms: a list
of values or a stepped sequence.
14
If we wanted the size of the model to vary in
step sizes of 100 we might write:
14
Rather confusingly, a stepped sequence is referred to as a number.
130 3 ABMs Using Repast and Java
<parameter name="size" type="number"
start="100" end="500" step="100" />
Note that the type of this parameter will be inferred to be int from the fact that
only integers have been used in defining the start, end and step values. If we
wanted to vary the number of human agents in powers of 10 then we might use the
following list form:
<parameter name="numHumans" type="list" value_type="int"
values="10 100 1000 10000" />
In general, we will often want to run the model with all values of one parameter
against all values of another parameter. This is achieved by nesting the parameter
specifications:
<parameter name="size" type="number"
start="100" end="500" step="100" >
<parameter name="numHumans" type="list" value_type="int"
values="10 100 1000 10000" />
</parameter>
Note that nesting requires that we use the form “</parameter>” to end the
outer parameter specification rather than “/>”.
3.4.16 Going Further with Repast S
With the two models we have developed in this chapter we have illustrated most of
the basic features of Repast that are necessary to get started writing practical models.
This is the case whether the choice is to use flowcharts to describe agent properties
and behaviors, or to handle these directly in Java source code. Nevertheless, within
a book such as this, it is only really possible to scratch the surface of what can
be done with Repast Simphony. Just the API is enormous, for instance. Some of
the features we do not have space to cover are things such as watchers, layers and
data in contexts. For the reader who wishes to develop sophisticated models with
Repast, it will be essential to make use of the official documentation available from
the Repast web site [35]. We would also strongly recommend joining the Repast
mailing list, where much help with practical issues is available.
Chapter 4
Differential Equations
Differential equations are the bread and butter of mathematical modeling in the sci-
ences. Many of the most fundamental equations in theoretical physics—the most
basic of all sciences—are differential equations. An important activity of physicists
is to formulate differential equations, solve them and interpret the solutions. Simi-
larly, in biological modeling differential equations are of high importance. They are
the right tool to describe many phenomena ranging from population dynamics and
chemical kinetics through to evolution and epidemiology.
This chapter will give the reader an introduction to the use of a specific type
of differential equations, namely ordinary differential equations (ODEs). The in-
troduction provided here is not intended as a replacement for substantive specialist
texts on this topic, such as Murray’s excellent volume “Mathematical Biology” [30].
Instead, this chapter aims to introduce the reader to both the power and limitations
of differential equations. The emphasis is twofold. Firstly, it will remind the reader
of the basic ideas of calculus and, following from that, motivate the underlying ideas
of a differential equations. It will also describe some elementary methods to solve
these equations. The second aim is to guide the reader through the exploration of
a few examples; by the end of this tour she will have developed a basic intuition
for the appropriate method to use and will be able to formulate her own models,
find solutions and analyze them. At the very least, she will have the background to
understand research papers on differential equation models.
We begin this tour with a brief introduction to the basic principles of calculus.
This introduction is primarily aimed at motivating ideas, rather than developing a
rigorous mathematical apparatus.
4.1 Differentiation
Consider the following question:
Kurt often travels from Graz (Austria) to Hermagor (also Austria). The trip takes him ex-
actly 2 hours and 20 minutes. The distance between the two towns is exactly 220 km. At
what speed does he travel?
D.J. Barnes, D. Chu, Introduction to Modeling for Biosciences,
DOI 10.1007/978-1-84996-326-8_4, © Springer-Verlag London Limited 2010
131

132 4 Differential Equations
The solution to this problem is easy enough, at least at a first glance. All one needs
to do is to divide the distance traveled by the time it takes to complete the trip.
Following this we can compute the speed to be v =60 ×
220 km
140 mins
≈94.3km/h.
Straightforward as it seems at first, there is a problem with this result. The curious
reader might take a look at the actual route taken by Kurt. She will then conclude
that this value is very unlikely to reflect the actual speed at which Kurt traveled at
any one time. For example, he started in Graz, which is a small town. In continental
Europe towns have a speed limit of 40 km/h. Assuming Kurt is a law abiding citizen
he would not drive faster than allowed by the law; we would therefore expect that
he stayed at or below the speed limit. On the other hand, a large part of the route is
a motorway (A2) with a speed limit of 130 km/h. Again, being impatient, Kurt will
normally try to keep at this speed. So, the 94.3 km/h we calculated as an average
speed, is not a very good estimate of the actual speed Kurt traveled. How can we
find a more realistic estimate?
One approach we can take is to divide the route into stages and measure the time
taken to complete these stages. As it turns, out, from Graz to Presseggen (which is
a village on the way) it took Kurt 2 hours and 13 minutes, which corresponds to an
average speed of 60 ×
213 km
133 mins
≈96.1 km/h. The remaining 7 kms from Presseggen
to Hermagor took a mere 7 mins, but at a speed of 60 km/h. The slower speed is
not surprising, because the last part of the trip is not on the motorway, but on a
countryside road (B111) with variable speed limits as it passes the villages on the
way. This last estimate is perhaps somewhat closer to the speed Kurt was traveling
during the last 7 minutes of his trip, before arriving; it certainly is quite different
from our first estimate of his speed as obtained above.
We can now draw a first conclusion: The speed averaged over the entire trip,
leading to an estimate of about 94.3 km/h is a poor guideline for the actual or typical
speeds Kurt traveled. As a matter of fact, he probably did not actually travel at this
speed for more than a small fraction of the entire time on the road, and was either
much faster (on the motorway) or much slower (in villages and cities). We can gain
a better idea of the actual speed traveled at various points in time by taking averages
over smaller distances. Averaging over only the last 7 km gave us a much better
estimate of the speed during the last part of the trip.
We can now take this insight further. In order to get a good estimate of the actual
speed traveled, we should further reduce the distance over which we average. So,
for example, Khünburg is 3.3 km from Presseggen en route to Hermagor. It took
Kurt exactly 3 mins to cover this distance. There is no need here now to repeat the
details of how to calculate the speed given a distance and time. Instead, we will now
introduce a new notation for this very familiar calculation. Let us write the distance
between the 2 villages as follows:
(Distance Khünburg-Graz) −(Distance Presseggen-Graz)
Time taken
=
3.3km
0.5hrs
=66 km/h
(4.1)
By “Distance Kürnburg-Graz” we mean the distance from Khünburg to the origin
of Kurt’s trip in Graz, which is 216.8 km; “Distance Presseggen-Graz” has a similar
