Barnes D.J., Chu D. Introduction to Modeling for Biosciences

Подождите немного. Документ загружается.

4.3 Differential Equations 153

Another, slightly clearer way of writing this is:

(x +ay) =0 (4.25)

This means that the expression x +ay is constant in time, because the derivative

is constant. Since (4.25) is true at any time during the evolution of the system, it is

certainly true at time t =0. Denoting x(0) by x

we get:

x +ay =x

+ay

(To interpret this equation, it is useful to remember that x is an abbreviation

for x(t).) We can now use this equation to express y as a function of x.

y =

+ay

−

(4.26)

We have now nearly succeeded in decoupling the differential equations in (4.24).

All that remains to be done is to substitute the newly found expression for y into the

differential equation for ˙x, abbreviating x

+ay

by b.

˙x =bx −x

(4.27)

We have now genuinely reduced the coupled system (4.24) to a single differential

equation. We only need to solve this differential equation because we can then obtain

the solution for y(t) by using (4.26).

The solution, as follows, can be obtained by using the separation of variables

technique again.

x(t) =

bC exp(bt)

C exp(bt) −1

(4.28)

4.9 Use the separation of variables technique to show that the solution for x(t) is

(4.28).

We still need to determine the integration constant C. As usual, we do this by

specifying the initial conditions.

x(0) =x

C −1

=⇒ C =

−x

−y

−b

4.10 What happens when x

=b?

The steady state behavior can again be obtained by considering the behavior at

inﬁnite times. In this case, the exponential terms become very large and the fraction

will approach 1. Therefore, at steady state, the size of the bacterial colony will be

given by,

x(∞) =b (4.29)

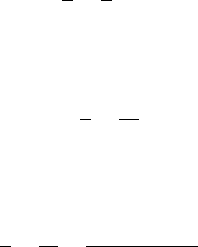
154 4 Differential Equations

We can obtain the same result directly from the differential equation (4.27) by ana-

lyzing the case of no change of the state variables, in this case ˙x =0.

˙x =0 =bx −x

=⇒ x =b

In addition to x

∗

= b the system also allows a trivial steady state given by x

∗

= 0

(steady states are commonly indicated by the variable name followed by a star).

Now that we have the solution for the time behavior of the bacterial colony, we

can also solve for the concentration of nutrients. For this we use our solution for

x(t) and (4.26).

y =

−

Just to convince ourselves of the soundness of the solution, let us check that the

initial and steady state values are correct.

∗

=y(∞) =

−

∗

This can be obtained by substituting the steady state solution of x(t) for x

∗

.Forthe

initial value we get,

=y(0) =

−

+ay

−x

For illustration, we plot the solution of our differential equation in Fig. 4.6 for

various initial conditions.

Note that, in this particular model the steady state depends on the initial con-

ditions. This is essentially due to the fact that there is a conserved property in the

model, as discussed above. This is not the typical case for differential equation mod-

els in biology. Normally, cells die or molecules are broken down. This introduces

dissipative elements into the model which prevent conservation relations from re-

maining valid. Yet, even when there are no conservation properties to be obeyed, it

can still be the case that the steady state depends on the initial conditions. This is

the case when the system supports more than a single steady state. This situation

partitions the phase space of the system into so-called basins of attraction for the

relevant steady states. We have already encountered a trivial example of this above,

in the case of the bacterial growth model. Any initial condition corresponding to no

bacteria being in the system causes the system to remain in this state forever. In this

instance, the basin of attraction corresponds to all states x(0) =0. We will see more

interesting examples of this below.

4.4 Case Study: Malaria

With these introductory remarks behind us let us now look in more detail at some-

what more advanced models. As a speciﬁc system let us consider a model of Malaria

4.4 Case Study: Malaria 155

Fig. 4.6 The dynamic behavior of (4.28)forx

= 0.01, a = 1 and various initial amounts of

nutrient

(or, in fact, any other vector borne disease) and its spread. Extensive details of a sim-

ilar model were given in Chap. 2, in the context of agent-based modeling. We have

vectors of infection (the mosquitoes) that infect humans by biting them; mosquitoes

are only infectious if they have been infected themselves. We assume that both

mosquitoes and humans remain infected for a certain amount of time before they

return to health again.

This rather qualitative information does not completely specify the differential

equation model we want to formulate, but it helps us to develop a ﬁrst model that

will then enable us to obtain an idea of the behavior of the system. We approach the

modeling process as in the examples above; that is, we start by thinking about how

changes in the variables affect the spread of an infection.

Considering the infection dynamics for humans ﬁrst. Qualitatively we can state

that the more infected mosquitoes there are, the more humans will get infected.

To be more precise: The greater the number of infected mosquitoes there are the

higher the chance per time unit that an uninfected human becomes infected. It is

unclear, at ﬁrst, exactly what the dependence of the infection rate on the prevalence

of infection among mosquitoes is. As a ﬁrst model and in the absence of better data,

we can assume linear proportionality. Since only uninfected humans can become

infected, we need to assume that the infection rates among humans also depend on

the number of uninfected individuals (rather than on the total number of humans).

Next we need to decide on how humans lose their infection. In reality, there are

two possible routes. Either one is cured or one dies. Once one has suffered a bout

156 4 Differential Equations

of Malaria one tends to acquire some immunity against the disease, making future

infections both less likely and less severe. Including this in a differential equation

model would require introducing a third category of humans beside the infected and

the uninfected ones. This is fully feasible, yet we are not primarily interested in

Malaria here, but in the general process of how to construct differential equation

models. Therefore, we will ignore this additional complicating factor. Similarly, we

will not explicitly model the fact that infected sufferers can die of the disease. Our

model population will be constant and we will assume that individuals lose their in-

fection after some time and return to the pool of uninfected individuals. Differential

equations can of course not keep track of individuals, but always consider large pop-

ulations. The way to model the “curing” process is to assume that infected humans

lose their infection at a certain constant rate. Formally, the problem is equivalent

to the case of protein decay above. In any time period, the actual number of curing

events will depend on the number of infected individuals as well as the curing rate.

Hence, altogether, the total rate of curing is proportional to the ﬁxed curing rate

constant and the number of infected humans.

As far as the mosquitoes are concerned, we can make exactly the same arguments

regarding the infection and curing rates, although with different proportionality con-

stants. This reﬂects that the infection dynamics of mosquitoes should be assumed to

be distinct, if for no other reason than that they live for a much shorter time.

Before we can formulate our model mathematically, we need to pay attention to

one detail. As far as the infection rate is concerned, what counts is not the absolute

number of infected individuals, but the proportion of infected individuals in the

entire population. To reﬂect this aspect in our model let us denote the proportion

of infected humans by s(t); the proportion of healthy individuals is then given by

1 − s(t), assuming that there are no states between healthy and sick. Similarly, let

us denote the proportion of infected mosquitoes by m(t); in close analogy with the

human population, the proportion of uninfected individuals is given by 1 − m(t).

By adopting this form, we do not need to write separate formulas for infected and

uninfected populations, since the proportion of infected and uninfected individuals

can be immediately obtained from one another.

Taking all this into account, we arrive at a differential equation model for Malaria

infection.

˙s =a(1 −s)m −bs

˙m = c(1 −m)s −dm

(4.30)

This model formulates our assumptions about the factors affecting the growth of

infections in Malaria. The ﬁrst term on the right hand side of the ﬁrst line reﬂects

the fact that the growth of the infections among humans depends on the size of the

uninfected population (represented by 1 −s) and the size of the infected mosquito

population m. Note that other terms also have parameters, denoted by a, b, c and d.

These system parameters assign weights to the various growth and shrinkage terms

and normally need to be measured (that is, they cannot be inferred by an armchair

modeler).

In this particular model, the parameter c can be interpreted physically. It sum-

maries two effects, namely the probability of transmitting a disease should a human

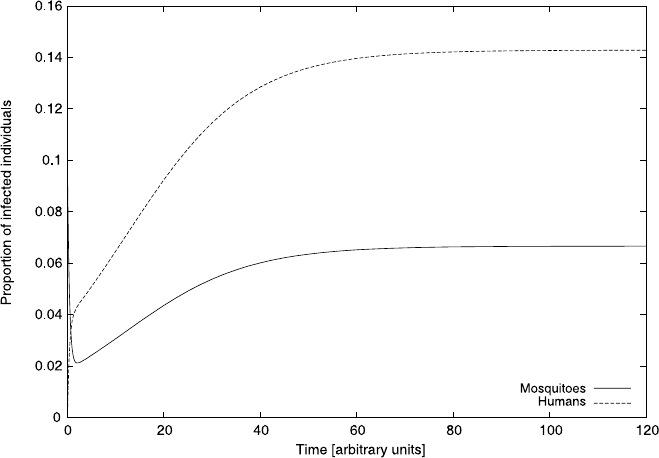
4.4 Case Study: Malaria 157

Fig. 4.7 A possible solution for the differential equation system (4.30) describing the spread of

Malaria. Here we kept the parameters, a =1, b =0.4, c =1, d = 2

be bitten by a mosquito, and the probability of a human being bitten in the ﬁrst

place should human and mosquito “meet.” The parameter a is interpreted in an

analogous fashion. The parameters b and d determine the rate with which humans

and mosquitoes, respectively, lose their infection.

Unlike the simpler models we have encountered so far in this section, this one

cannot be solved analytically with elementary methods, and we will therefore not

attempt to do so. This is a pity, but it is the norm for the typical model one tends to

encounter in biology. Luckily, nowadays it is easy to obtain numerical solutions to

differential equation models using computer algebra systems, such as Maxima (see

Chap. 5). The disadvantage of this approach is that, in order to generate a solution,

we need to specify values for all the parameters of the model (a,b,c,d). Any so-

lution we generate is only valid for this particular set of parameter values, and the

behavior can be quite different for other sets of values (Fig. 4.7). Unless the parame-

ters are well speciﬁed, for example experimentally measured, one has to spend quite

some time exploring the possible behaviors of the model by generating numerical

solutions for many combinations of parameters.

Even when an analytic solution is not possible using elementary techniques

alone, one can still often extract some useful general information about the behav-

ior of the system by analyzing its steady state behavior. We can easily calculate the

steady state behavior by setting ˙s =0 and ˙m = 0 and solve the resulting system of

equations in (4.30). From this we obtain a solution for the steady state behavior of

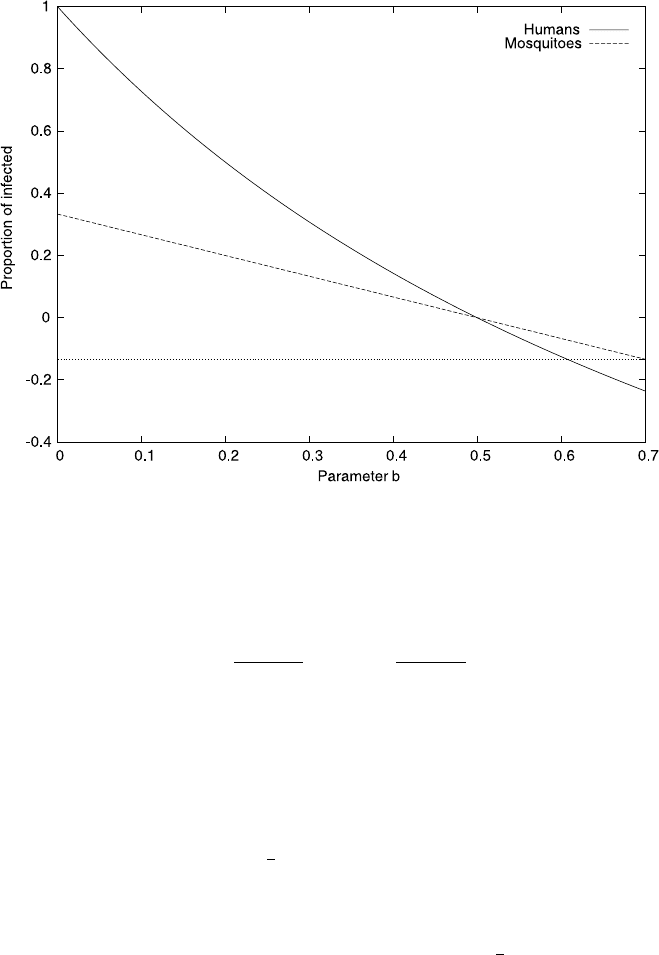
158 4 Differential Equations

Fig. 4.8 The steady state infection levels for mosquitoes and humans of the model equation (4.30);

these two curves illustrate (4.31). Here we used the parameters, a = 1, c = 1, d = 2ﬁxedand

varied b

the model in terms of the parameters.

∗

ca −db

c(a +b)

∗

ca −db

a(c +d)

(4.31)

Figure 4.8 illustrates how the steady state varies with b when we keep the other

parameters ﬁxed at a =1, c = 1 and d =2. From the ﬁgure it is clear that positive

solutions can only be obtained when b<0.5. This can also be seen from (4.31).

If we substitute the chosen values of a,c and d into the ﬁrst equation, then we

obtain the steady state number of infected humans, s

∗

, in terms of b. If we then

set s

∗

= 0 we obtain the value of the parameter b where the steady state reaches

zero. This point is exactly at b =

. For this value, or indeed larger values of b any

infection that may be introduced into the system will eventually disappear again.

Note, however, that a steady state corresponding to vanishing infection levels is

fully compatible with transient periods where Malaria is present in the system.

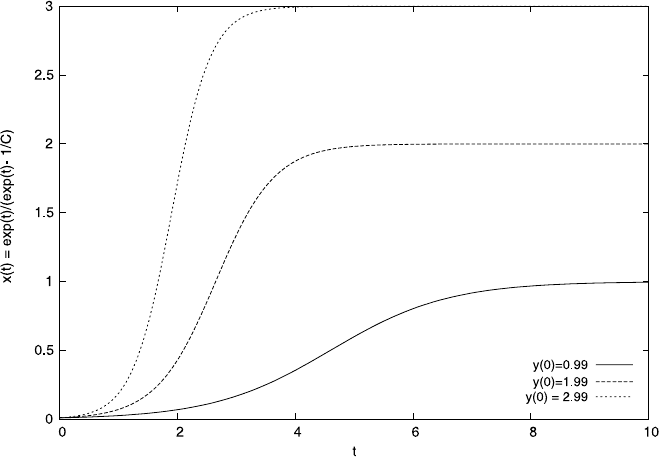
Figure 4.9 illustrates this. Here we set the parameter b =

, which means that

in the long run any infection will die out. The graph shows an example where at

time t = 0 all the humans and 10% of the mosquitoes are infected. Despite the

fact that the infection is not sustainable in the long run, initially the model even

leads to an increase of the infection levels among the mosquitoes. The levels fall

only after some time. In this particular case, the rates of decline of the infection are

4.4 Case Study: Malaria 159

Fig. 4.9 The transient behavior of model equation (4.30). We started with initial conditions where

all humans and 10% of mosquitoes are infected. We used the parameters, a = 1, b = 0.5, c = 1,

d =2. Initially, the infection level of mosquitoes even rises before it eventually falls

very high at ﬁrst, but eventually the fall in infections becomes slower and slower.

As a result, even after long transient periods there is still a low level of infection

in the system. Malaria will only be eradicated completely after inﬁnite amounts of

time have passed although, in practice, infection levels will be very low after a long

but ﬁnite time. We have encountered this type of slow approach of the steady state

above.

In biological modeling, one is normally only interested in a subset of the math-

ematically possible solutions of differential equations. Typically one wishes to pre-

dict quantities such as concentrations of molecules, particle numbers or, as in the

present case, infection levels. These quantities are all described by positive real

numbers. Similarly, the space of possible or meaningful values of parameters is of-

ten restricted by the physical meaning. For example, as far as the Malaria model is

concerned, we are only interested in positive values for the four parameters a, b,

c and d of the system. These all represent proportionality constants and it would

not makes sense to set any of these to negative values, even though mathematically

there is no reason not to do this. A negative value for any of these parameters would

completely pervert the meaning of the model.

We should, however, spend some time thinking about the areas where our

model might predict negative infection rates, which would make no physical sense.

A glance at Fig. 4.8 reveals, rather troublingly, that for b>

there will be a negative

steady state. The reader is encouraged to convince herself of this using (4.31).

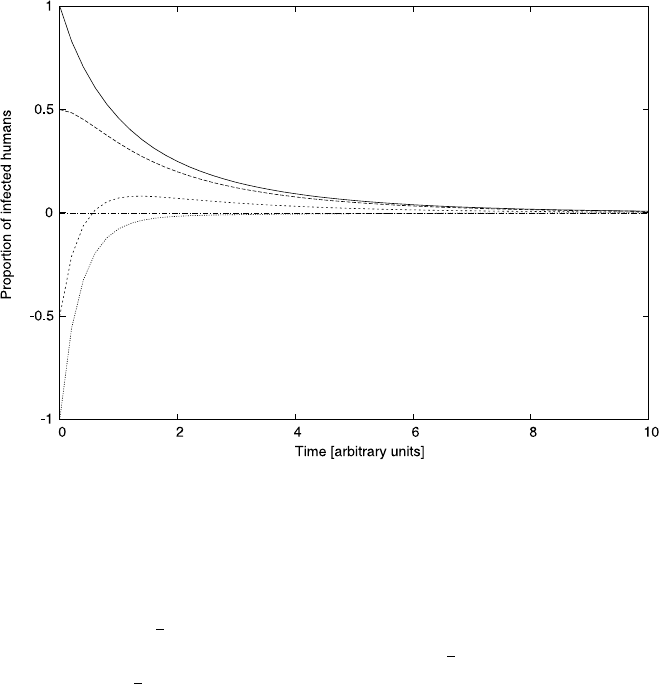
160 4 Differential Equations

Fig. 4.10 The transient behavior of model equation (4.30) for various initial conditions. We used

the parameters, a =1, b =0.6, c =1, d =2, and an initial condition of m(0) =1

This is potentially a problem for the interpretation of the model with respect

to the real situation. There is nothing inherently unphysical or unreasonable about

assuming that b>

; the parameter b simply formulates how fast people recover

from Malaria. It might well be that in real systems b<

, but this does not change

the fact that b>

still is a meaningful choice of parameter. Still it seemingly leads

to the unphysical prediction of negative infection levels in the long run. If this was

indeed so, then this would indicate a problem of the model: There is no use having

a model that sometimes produces unrealistic behavior.

Let us see what happens when we increase the parameter b beyond 0.5. Fig-

ure 4.10 illustrates the dynamics predicted by the model for b =0.6 for various ini-

tial conditions ranging from s(0) =−1tos(0) = 1 (all graphs shown assume that

m(0) = 1). All the example curves we plotted predict that, in the long run, infec-

tions among humans will vanish, that is the negative steady state is not approached

after all. If we start with negative infection rates then, at least for a transient time

s(t) < 0 but again in the long run, infection levels tend to zero. The negative tran-

sient levels are neither surprising nor disconcerting. After all, by choosing initial

conditions corresponding to physically unrealistic values, we provided garbage as

input, and are accordingly rewarded with garbage as output. On the other hand, if

we start with the physically realistic initial conditions, that is 0 ≤s(0) ≤1 then the

model predicts positive infection rates throughout, only tending to zero in the long

run. This is reassuring. It is not watertight evidence for the correctness of the model

4.4 Case Study: Malaria 161

(whatever we mean by “correct”), but, at least it means that if fed on reasonable

input, the model does not produce meaningless output.

While we can feel a little reassured about the predictions of the model in this

particular case, we should start to have some doubts about the predictions of the

steady state behavior of the model. Following our steady state analysis in (4.31) and

Fig. 4.8 we would expect the model to show a negative steady state. This is clearly

not what we observe, at least in the example depicted in Fig. 4.10.

One immediate resolution for this apparent discrepancy is that the system allows

more than two steady states, as discussed above. One of them corresponds to vanish-

ing infection levels in both mosquitoes and humans, or simply s

∗

=0. While

trivial, this is a physically realistic steady state. The second, for b>0.5, corresponds

to physically infeasible solutions s

∗

< 0 and m

∗

< 0.

In order to understand the situation in more depth, it is necessary to introduce a

new concept, namely that of stability of a steady state point. Mathematically, much

is known about the stability of steady state points. A thorough treatment of the

topic that would do justice to the wealth of available knowledge is far beyond the

scope of this book. The reader who wishes to deepen her knowledge on this issue

is encouraged to consult a more advanced text such as Casti’s excellent and very

accessible two volume “Reality Rules” [5, 6]. Yet, even without entering the depths

of dynamical systems theory, it is possible to convey the main ideas. Despite being

elementary this basic understanding is often sufﬁcient to master the demands of real

world modeling enterprises in biology.

4.4.1 A Brief Note on Stability

Let us assume a population of uninfected humans and mosquitoes, i.e., s(t) =

m(t) = 0. Clearly, unless Malaria is somehow actively introduced into the system,

the infection levels will remain at zero for all time. The question we want to ask

now is the following: What happens to the system if we introduce the infection into

the system at a small level, for example by releasing a few infected mosquitoes, or

by the arrival of a few people who carry Malaria?

There are two answers to this question: (i) It could be that an infection will gain

a foothold and establish itself. Alternatively, (ii) it might not establish itself and the

system reverts, after a short spell of Malaria, to the state where s(t) = m(t) = 0.

In essence, this is the intuition behind what mathematicians call the stability of a

steady state point of a system of differential equations: How does a system at steady

state respond to a small disturbance. The ﬁrst case, where a small disturbance to

the steady state spreads and leads to the infection establishing itself in the long run,

represents the case where the steady state corresponding to m

∗

=0 is unstable.

The second case, where the disturbance does not spread, the steady state is stable. In

general, when modeling biological systems, we are interested in stable steady states,

because these are the ones we will observe in reality. Real systems are permanently

subject to more or less violent shocks that push them away from any unstable steady

162 4 Differential Equations

states they might inhabit. Unstable steady states persist just as long as a ping-pong

ball would rest at the top of a convex surface, or a pool cue would remain upright

balanced on its tip when exposed to a slight draught or vibration.

As it turns out, there is a fairly simple method to determine the stability of a

steady state. It is based on determining the eigenvalues (see Appendix A.5.1)ofthe

Jacobian matrix of the system at the steady state. Again, very much is known and

can be said about the stability of dynamical systems (this is what systems of differ-

ential equations are sometimes called). However, much can be done with elementary

methods that can be learned with relatively little effort. In the following paragraphs

we will therefore introduce some methods that can be applied without going into

the theory of the topic. Nevertheless, the reader is urged to eventually consult more

specialized volumes to acquire more sophisticated skills backed up by a thorough

understanding of the theoretical background.

Before describing how to determine the stability of steady states, we need to

brieﬂy deﬁne what the Jacobian matrix is. Assume a system of differential equations

of the general form:

˙x

,...,x

) (4.32)

˙x

,...,x

) (4.33)

... (4.34)

˙x

,...,x

) (4.35)

This system of equations is nothing but a generalized form of the differential equa-

tions we have encountered before. In the Malaria model (4.30)wehavetotake

≡s and x

≡m, f

(s, m) ≡a(1 −s)m −bs and so on.

Using this form the Jacobian is deﬁned as the n × n matrix of derivatives of f

with respect to x

i,j

(x) =

∂f

,...,x

)

∂x

(4.36)

In the case of n =3, for example, the Jacobian would be a 3 ×3 matrix.

J(x

) =

⎡

⎢

⎣

∂

∂x

)

∂

∂x

)

∂

∂x

)

∂

∂x

)

∂

∂x

)

∂

∂x

)

∂

∂x

)

∂

∂x

)

∂

∂x

)

⎤

⎥

⎦

(4.37)

The basic structure of a Jacobian matrix is very simple. It is a list of derivatives

of the right hand sides of the differential equations with respect to all the system

variables.

It is not the Jacobian directly that provides insight into the stability properties of

a steady state, x

∗

=(x

∗

,...,x

∗

), but rather the set of eigenvalues E of the Jacobian

matrix at the relevant steady state, i.e., the matrix J(x

∗

). The members in the set E

are numbers, possibly complex numbers, although we are primarily interested in the