Басниев К.С. Энциклопедия газовой промышленности

Подождите немного. Документ загружается.

СНГ

5.6.

СЖИЖЕННЫЕ НЕФТЯНЫЕ ГАЗЫ И БЕЗОПАСНОСТЬ

По своим характеристикам сжиженные нефтя-

ные газы представляют всегда значительный го-

рючий потенциал, часто весьма значительный. Их

хранение,

перекачка, транспорт сопровождаются

особыми опасностями, с которыми хорошо должно

быть

знакомо каждое предприятие, для того

чтобы

ними справиться.

Существует строгая регламентация относитель-

но строительства, оборудования и эксплуатации

складов, изготовления материалов и транспорта

продуктов.

Помимо

необходимости строгого соблюдения

этой

многочисленной

регламентации,

многочислен-

ные правила производства работ, формализиро-

ванные

или нет (директивы, правила, способы про-

ведения работ и

т.д.),

должны строго соблюдаться.

Особое внимание должно

быть

уделено обору-

дованию, обслуживанию и обучению в процессе

работы:

— средства защиты (надежные электрические це-

пи,

равнопотенциальные соединения и

зазем-

ление,

средства безопасности, обнаружения

утечек

газа,

загородки, вывески и

т.п.);

— устройства безопасности (клапаны-отсекатели

предохранительные клапаны, обратные кла-

паны, пневматические или гидравлические се-

ти

безопасности, дренажные линии и

т.д.);

— средства противопожарной защиты (водоводы,

брандспойнты, оросительные системы, огнету-

шители

т.п.);

— персональные средства защиты (специальные

рукавицы, очки, огнестойкая одежда, противо-

искровая

обувь,

огнезащитная одежда, каски с

защитным

экраном и

т.п.).

Каждый,

кто эксплуатирует или имеет дело с

СНГ, должен

быть

соответствующим образом обу-

чен,

осознавать опасность и соблюдать правила,

он должен

быть

в состоянии постоянной готовнос-

ти

защите.

534

ТРАНСПОРТ

ПО ТРУБОПРОВОДАМ

6.1.

КОНЦЕПЦИЯ ТРАНСПОРТНОЙ СЕТИ

6.1.1.

Определение

Транспортные сети представляют собой соору-

жения,

предназначенные для транспорта

газа

под

высоким давлением между одним или нескольки-

ми

источниками и одним или несколькими потреби-

телями с определенным числом более мелких про-

межуточных потребителей.

В это определение входят:

— международные газовые

сети;

— ответвления от транспортных сетей и местные

сети

газоснабжения.

Концепция транспортной сети включает опреде-

ление

конфигурации сети и оптимальных характе-

ристик

сооружений, состоящих из трубопроводов и

компрессорных станций. Стоящая проблема вклю-

чает

разнообразные исходные и физические дан-

ные, которые оставляют место для разнообразных

решений,

среди которых критерий

выбора

позво-

ляет находить наилучшее решение.

6.1.1.1.

Данные

Исходные данные:

— физические характеристики транспортируемо-

го

газа;

— расположение источника и условия получения

газа

в этой точке;

— расположение и характеристика потребителей

газа;

— количество транспортируемого

газа.

Если рас-

ход

газа

не постоянен, то необходимые исход-

ные данные должны

быть

определены предва-

рительным расчетом.

6.1.1.2.

Характеристики, которые

должны

быть

определены

Характеристики

транспортной сети следующие:

— структура сети и трассы трубопроводов;

— максимальное рабочее давление и диаметры

газопроводов;

— место расположения и мощность компрессор-

ных станций.

6.1.1.3.

Физические уравнения

проблемы

Физические

уравнения решения проблемы

включают:

— поддержание расхода в каждом узле

сети.

Эти

решения

необходимы для определения режима

движения

газа

по рассматриваемой

сети.

Ука-

занные уравнения недостаточны в случае за-

кольцованной

сети;

— уравнения потерь давления, которые связыва-

ют распределение давления на расчетном уча-

стке

с определенной длиной, диаметром и рас-

ходом.

Кроме указанных выше, необходимы

следующие

параметры: физические характери-

стики

газа,

температура

газа,

шероховатость

трубопровода, характеризующая состояние

внутренней поверхности трубопровода, и преж-

де

всего

профиль

трассы;

— формулы, дающие возможность определять

мощность в зависимости от давления на входе

выходе

из компрессорной станции и расхода

газа.

Физические характеристики

газа

и темпе-

ратура на всасывании компрессора. Для расче-

та

мощности привода компрессора необходимо

учитывать

высоту

расположения станции над

уровнем моря и температуру наружного воз-

духа.

535

ТРАНСПОРТ ПО ТРУБОПРОВОДАМ

6.1.1.4.

Критерии

выбора

Среди различных вариантов, отвечающих про-

блеме (т.е. исходным техническим данным), эконо-

мический критерий должен позволить

выбрать

оп-

тимальное решение. В общем эта оптимизация со-

стоит в нахождении решения, которое дает

максимальную

прибыль

и еще постоянный доход в

соответствии с

выбранным

решением, минималь-

ные текущие расходы (стоимость транспорта мини-

мальная). В том случае, если предприятие

из-за

финансовых

сложностей не может

получить

мак-

симальную

прибыль,

можно принять как оптималь-

ный критерий степень получения максимальной

прибыли (отношение доходов от реализованного

проекта к сумме капвложений).

Надо заметить, что экономические критерии не

могут корректно применяться, когда различие

между

несколькими решениями незначительно

(учитывая неопределенность экономических гипо-

тез).

Тем не

менее,

другие факторы, трудно оцени-

ваемые экономически, должны

быть

учтены

при

принятии решения:

— надежность и безопасность разных решений;

— нагрузка на окружающую среду.

Здесь

будет рассматриваться

только

экономи-

ческий критерии т.к. другие элементы

выбора

рас-

сматриваются в

особых

случаях.

6.1.1.5.

Общая методика рассмотрения

концепции транспортной сети

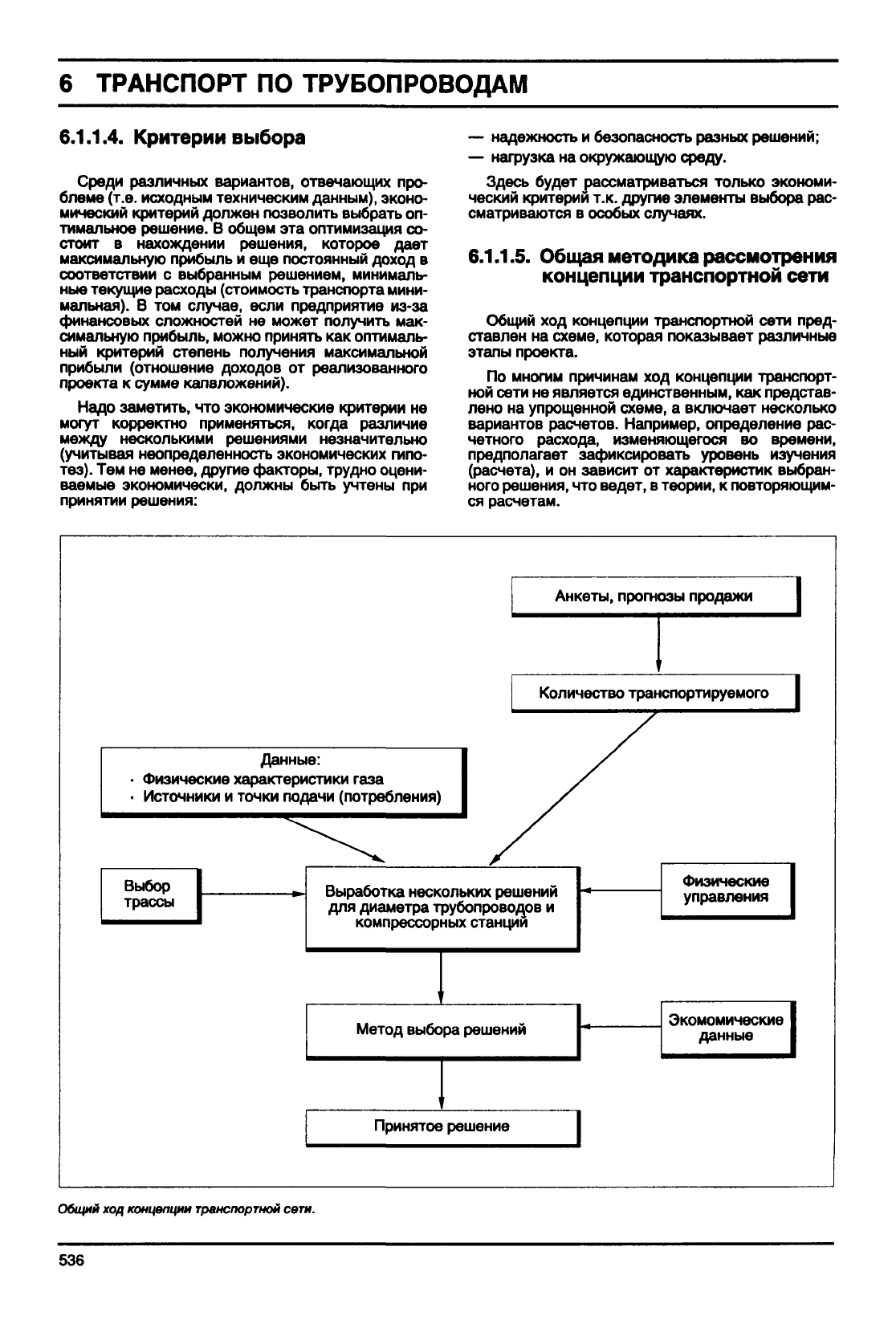
Общий ход концепции транспортной сети пред-

ставлен на схеме, которая показывает различные

этапы проекта.

По многим причинам ход концепции транспорт-

ной сети не является единственным, как представ-

лено на упрощенной схеме, а включает несколько

вариантов расчетов. Например, определение рас-

четного расхода, изменяющегося во времени,

предполагает зафиксировать

уровень

изучения

(расчета),

и он зависит от характеристик выбран-

ного решения, что ведет, в теории, к повторяющим-

ся расчетам.

Данные:

• Физические характеристики

газа

• Источники и точки подачи (потребления)

Выбор

трассы

Анкеты, прогнозы продажи

Количество транспортируемого

Выработка нескольких решений

для диаметра трубопроводов и

компрессорных станции

Метод

выбора

решений

Принятое решение

Физические

управления

Экомомические

данные I

Общий

ход

концепции

транспортной

сети.

536

ТРАНСПОРТ

ПО

ТРУБОПРОВОДАМ

Проблемы экономики ставят также вопросы:

нужно ли уложить газопровод с диаметром D поз-

воляющим подавать клиентам газ N лет, подразу-

мевая,

что затем прокладывается

новый

парал-

лельный

газопровод диаметром D' для снабжения

клиентов еще N'

дополнительных

лет или сразу по-

ложить газопровод диаметром D'(D* > D), который

будет

полностью

загружен

только

через N + N'

лет? Второе решение, которое требует более

высоких

капвложений, тем предпочтительней:

— чем ниже процент реализации,

— чем стоимость постоянной части цены строи-

тельства трубопровода больше части стоимос-

ти,

зависимой от диаметра (особенно в случае

небольшого диаметра).

В случае сложной задачи (например, определе-

ние характеристики нового сооружения внутри су-

ществующей закольцованной сети) это комплекс

последовательных решений, которые должны по-

вторяться

несколько раз, рассматривая разные

варианты: различные расходы в точке врезки в за-

висимости от климатических условий, прекраще-

ние газоснабжения от одного из источников и т.д.

Использованные методы реализации концепции

транспортной сети рассматриваются ниже.

6.1.2.2.

Расход,

изменяющийся

во

времени

Это участки газопроводов или ответвления ре-

гионального уровня, для которых увеличение про-

дажи

приводит со временем к увеличению рас-

хода.

Прогноз продажи

газа

через коммерческие

предприятия для среднеклиматического года

включает:

— потребление "вне отопления" (вне дополни-

тельного потребления в

холодный

период

H.C.S.P.F.);

— потребности систем отопления (потребление

дополнительное в отопительный период

C.S.P.F.).

Схематически по методике "градиент" расчет-

ный расход представляет сумму

двух

составляю-

щих:

— первая составляющая - это максимальный

часовой расход на коммунально-бытовые

нужды без отопления

H.C.S.P.F.

6.1.2.

Определение

расчетного

расхода

газа

Рассматриваются два случая, когда расход

газа

постоянный и переменный во времени.

6.1.2.1.

Расход

газа

постоянен

определен

процессе

проектирования

Это характерно:

— для международных газопроводов, соединяю-

щих

источники снабжения с границей;

— для

национальных

газопроводов, являющихся

источниками поставки определенного количе-

ства

газа.

В этих случаях годовая поставка

газа

определя-

ется контрактом Q,, а часовой расход Q

опреде-

ляющий размеры сооружений равен:

~ 8

760m

где:

m - коэффициент колебания расхода, который

учитывает гибкость контракта и, в первую оче-

редь, степень безопасности.

Расход Q может

быть

округлен в

большую

сто-

рону для увеличения гибкости работы. Величина т

обычно

составляет 0,85 - 0,9.

где:

- газовое число часов использования

газа;

обычно

составляет

5500

7000

часов

— вторая составляющая - это максимальный

часовой расход

газа

на отопление

C.S.P.F.

(Т.-Т^

где:

Т, - температура, ниже которой появляется рас-

ход

газа

на отопление;

Ту- среднегодовая дневная температура;

- число часов работы в день. Представляет су-

точное изменение потребностей;

- расчетная температура, которая в зависимос-

ти от климата должна перекрываться с опреде-

ленным риском ее возникновения;

Т, - различается для регионов и составляет от 14°

ДО17°С;

- равно 15 часам для малых ответвлений и

часам для больших транспортных

сетей.

6.1.3.

Выбор

трассы

Знание

расположения источника и точки или то-

чек

потребления позволяет определить трассу или

трассы, которая позволяет определить:

— длину различных отрезков газопровода;

— характеристику фунта, что позволит опреде-

лить

стоимость прокладки трубопровода.

537

ТРАНСПОРТ ПО ТРУБОПРОВОДАМ

6.1.4.

ФиЗИЧеСКИе

уравнения

6.1.4.1.2. Формула Колебрука (обычная)

6.1.4.1.

Формулы потерь давления

Обычно пренебрегают местными потерями по

сравнению с линейными потерями. Эти последние

могут

определяться по формулам, которые для го-

ризонтального газопровода представляются в виде

где:

- константа, величина которой зависит от раз-

мерности

давления и условий (температура,

давление) определения расхода. При стандартных

условиях для давления в бар 1 атм (1013 бар) и

0°С, К - 6 000 Р, и Р

- давление в

начале

и конце

участка соответственно;

Оо - часовой расход газа с учетом температуры и

давления;

L - длина участка (в км);

D - внутренний диаметр трубопровода (в мм);

5- плотность

газа;

- средняя температура газа (К);

- коэффициент сжимаемости газа для среднего

давления и средней температуры транспортируе-

мого

газа;

Х- коэффициент трения, зависящий от числа Рей-

нольдса (R.) и относительной шероховатости —,

где

е-абсолютная шероховатость.

6.1.4.1.1.

Формула Панхандля

Формула

Панхандля

не включает коэффици-

ент X, как функцию от числа R. и относительной

шероховатости, т.к. используется эмпирическая

формула:

Х =

°'

о1о7

[о-;

где

v - кинематическая вязкость

газа,

сантистокс;

- полином в D и в (величина Е

от 0,7 до 1,0).

Таким образом

что позволяет использовать в расчетах формулу

, -rz M

й039

V-

288lo,16 J I Ep J

Коэффициент потерь давления дается в виде

неявной формулы

1 _ 2

3.71D

6.1.4.1.3.

Улучшенная формула Колебрука

В ходе экспериментов было установлено два ти-

па турбулентного режима: режим частично турбу-

лентный для числа Рейнольдса ниже 10

и режим

полностью турбулентный для числа R, выше этой

величины. Это приводит к новой формулировке

коэффициента потерь давления в формуле Колеб-

рука

(эта формулировка X явная).

*•-*•

Г5.оз!дя.-4,32^']

{

R; ) у

К, - 3,941 К.

где:

tf - шероховатость в явном виде в микрометрах,

принимаемая в расчет, и плюс шероховатость всех

элементов, могущих создавать турбулентность при

течении флюидов;

f- фактор торможения близкий 1, принимающий в

расчет

изгиб

трубопровода и состояние его внут-

ренней поверхности.

Эта последняя формулировка кажется

лучше

всего

подходит для обычных условий транспорта.

6.1.4.2.

Формулы для расчета

мощности

сжатия

Точная

методика состоит в последовательном

расчете:

— теоретической мощности при адиабатическом,

изотермическом

или политропическом процес-

се

сжатия;

— реальной мощности сжатия путем деления тео-

ретической

мощности на адиабатический, изо-

термический

или политропический КПД (в соот-

ветствии с выбранной теоретической форму-

лой) - для

того,

чтобы учесть необратимость

термодинамических процессов, так же как

внешний КПД, чтобы учесть механическое тре-

ние;

— мощности на

валу,

необходимой для определе-

ния реальной мощности привода, путем округ-

ления ее в большую сторону с учетом влияния

вспомогательных устройств антипульсаторов и

других

причин потерь мощности.

Практически,

на стадии проекта можно исполь-

зовать упрощенную формулу непосредственно для

определения по

валу:

w =

»(li)&)

p7'

где:

W - необходимая мощность по

валу,

кВт;

Оо - расход сжимаемого газа нм

/ч;

538

ТРАНСПОРТ ПО ТРУБОПРОВОДАМ

и Р, - давление нагнетания и сжатия;

- среднеарифметическое значение коэффици-

ента сжимаемости при условии всасывания и на-

гнетания;

Т, - абсолютная температура на всасывании.

Значение величины К дается в таблице:

\. Р,

Тип компрессора ^^^^

Поршневой компрессор

Центробежный компрессор

От 1,3 до 2,0

0,085

0,095

От 2,0 до 3,0

0,095

0,100

6.1.5.

Экономические данные

6.1.5.1.

Определение капвложений

6.1.5.1.1.

Трубопроводы

Стоимость трубопровода может

быть

представ-

лена

тремя составляющими:

— поставка неизолированных труб с завода;

— укладка труб (подготовка трассы, рытье тран-

шеи,

раскладка труб, сварка, укладка в тран-

шею, засыпка, сдача в эксплуатацию);

— разнообразные элементы строительства: изо-

ляция, транспорт и хранение труб, разнообраз-

ные работы.

В общем, капитальные вложения в единицу дли-

ны трубопровода диаметром D могут выразиться

одной из

двух

следующих

формул

(давление и ди-

апазон диаметров, для которых формула может

применяться, зависят от числа уточняющих пара-

метров).

Приблизительные величины уточняющих пара-

метров для условий среднего строительства со-

ставляют:

— фиксированная часть соответствует примерно

25%

общей стоимости трубопровода диаметром

400 мм;

-с=

1,5;

— в • 0,65 для

малых

диаметров (5300);

— в

1,3 для больших диаметров

(£400).

6.1.5.1.2.

Компрессорные станции

Капитальные вложения одной компрессорной

станции включают:

— одна часть, пропорциональная числу установ-

ленных

компрессоров, которые соответствуют

стоимости

машин, здания и их коммуникаций;

— вторая часть - постоянная В, соответствующая

общим газопроводам и общеинженерным соору-

жениям.

Первая

часть зависит от единичной мощности

установленных машин, вторая часть - от общей

мощности.

Более просто, можно удовлетвориться

формулой типа:

где:

W - общая мощность, или еще,

Приблизительная величина параметра уточ-

нения

х - 0,65.

Фиксированная часть В представляет примерно

30%

общей стоимости станции.

6.1.5.2.

Оценка годовых

эксплуатационных расходов

N на экс-

Различают, с одной стороны,

плуатацию и на рабочую силу, с другой стороны,

расходы энергии (для привода компрессоров).

6.1.5.2.1.

Расходы на эксплуатацию

персонал

Эти годовые расходы принимаются, как заранее

оговоренный процент от суммы капитальных вло-

жений,

и составляют:

— для трубопроводов - до 3%;

— для компрессорных станций - от 3 до 5%.

6.1.5.2.2.

Энергетические затраты

Необходимая энергия сжатия зависит от кривой

изменения расхода во времени. Кроме некоторых

особых

случаев

(расход постоянный или монотон-

ный,

близкий к линейному) подсчет энергетичес-

ких затрат состоит в определении плановой про-

граммы использования компрессорной станции на

основе программы транзита газа. Определяют рас-

ход энергии для отрезка времени и путем суммиро-

вания - годовой расход энергии.

6.1.5.3.

Экономические критерии

Применение предыдущих

формул

позволяет оп-

ределить:

— сроки окупаемости капитальных вложений,

— сроки окупаемости (реестра) эксплуатационных

расходов, которые имеют место в течение все-

го

срока реализации проекта.

Общие приведенные

реальные

расходы получа-

ются из этих

двух

составляющих путем примене-

ния к общим расходам (капвложения плюс эксплу-

атационные расходы) п-го года коэффициента при-

ведения, равного ; затем суммированием

(1+а)"

539

ТРАНСПОРТ ПО ТРУБОПРОВОДАМ

для всех лет рассматриваемого (а - коэффициента

приведения (актуализация)).

6.1.6.

Метод

определения

оптимального решения

Для принятия оптимального решения проблемы

транспорта газа

(см.

предыдущий параграф), могут

быть

применены два метода:

— метод

дифференциальных

расчетов;

— метод замены

реальных

сложных проблем ис-

кусственными,

упрощенными (моделирование).

6.1.6.1.

Метод

дифференциальных расчетов

Этот классический подход для решения про-

блем оптимизации систем под напряжением

(давлением).

случае

транспорта газа с учетом сложности

постановки

включающей большое число нелиней-

ных уравнений, необходимо значительно упрос-

тить оптимизируемые функции (экономические

критерии),

число влияющих факторов и парамет-

ров при необходимости получения полного реше-

ния.

Поэтому метод

дифференциальных

расчетов

применяется редко, при решении типовых про-

блем.

6.1.6.2.

Метод

моделирования

Он состоит в нахождении определенного числа

вариантов, относящихся к характеристике транс-

портной

сети (трасса, диаметр трубопроводов, чис-

ло, место расположения, мощность компрессорных

станций),

затем в расчете каждого варианта транс-

порта в соответствии с последовательностью схе-

мы,

представленой в § 6.1.1.5. Это ведет к

опти-

мальному решению, если варианты

были

выбраны

достаточно исчерпывающе.

Этот метод подходит ко всем достаточно слож-

ным исходным данным. Его основной недостаток:

продолжительность расчета, устраняемый по мере

применения ЭВМ.

Обоснованность принятых

гипотез,

полнота

выбранных для изучения вариантов, критический

анализ соответствия

полученных

результатов с

учетом их чувствительности к неопределенности

исходных

данных,

остаются основными условиями

качества исследования, выполненного по методу

моделирования.

6.1.7.

Классические

результаты

типовых

проблем

дифференци-

ального

метода

6.1.7.1.

Общие упрощенные гипотезы,

используемые для решения

типовых

проблем

6.1.7.1.1.

Физические уравнения

6.1.7.1.1.1.

Трубопроводы

Общая

формула, используемая для расчета по-

терь давления, с обозначениями § 6.1.4.1

„г

где

К, - const.

Это значит, что пренебрегают всеми изменения-

ми

К, в зависимости от диаметра, состояния трубо-

провода,

физических условий температуры,

давления, расхода и природы

газа.

Применяя эту

гипотезу

постоянства коэффициента, можно рас-

считать диаметр одного трубопровода, эквива-

лентного нескольким

параллельным

трубопрово-

дам такой же длины и диаметром D/ или

(

2/5

6.1.7.1.1.2. Компрессорные станции

Общая

формула, используемая для расчета

мощности

компрессора с обозначениями § 6.1.4.2

Q log

где

= const.

Здесь

также не учитывается изменение, вызы-

ваемое условиями температуры на всасывании и

физическими

характеристиками газа (коэффици-

ент сжимаемости).

6.1.7.1.2.

Экономическая зависимость

Общие и

отдельные

гипотезы, применяемые для

определения экономических критериев, состоят в

том,

что относительные расходы, капитальные

вложения, относящиеся к транспортной

сети,

име-

ют место в одно и то же время. Это позволяет

только обосновать нахождение общих годовых

расходов сложением эксплуатационных расходов

с капитальными в виде амортизационных отчисле-

ний,

которые сами пропорциональны чистым

капи-

тальным

вложениям.

6.1.7.1.2.1.

Трубопроводы

Годовые расходы для участка трубопровода ди-

аметром D и длиной L, обозначенные как D сапа,

может выражаться формулой

D сапа = Я сапа = /(а + ЬО%,

540

ТРАНСПОРТ ПО ТРУБОПРОВОДАМ

где:

фактор, который включает коэффициент амор-

тизации

коэффициент расходов

на

персонал

эксплуатацию.

6.1.7.1.2.2.

Компрессорные станции

коды компрессорной станции,

обо-

значаемой

соглр, может выражаться формулой:

comp

- П

сотр

+ eW,

где:

фактор, включающий коэффициент амортиза-

ции

расходы

на

персонал

обслуживание,

фактор, который включает стоимость энергии,

отношение

среднего расхода

предельному

КПД

привода

число часов работы

в год.

Капитальные вложения

для

строительства

од-

ной компрессорной станции определяются

по фор-

муле

comp met

+ &W,

мощность сжатия

формулой

- К log r,

где:

Годовые

расходы

для

одной станции выразятся

формулой:

comp

> fa' + {ft/ +

e)K

log r

или

соответствии

классической теорией

comp

- С + 2AQ log г.

6.1.7.2.

Случай транспорта

со

сжатием

в одной точке

в начале трубопровода

Схема

обозначения

для

типовой задачи пред-

ставлены ниже.

Диаметр

О, Длина L

РасходО

Поиск минимума

F - С + 2А Q log

•=-

I + i(a +

при потерях давления Р

-Р

—

приводит

отношению

Р?

5AQ

-2е/5

Это

отношение позволяет определить опти-

мальное давление нагнетания

Pi,

если известен

расход

длина,

также необходимое давление

на-

гнетания

Находят

оптимальный диаметр

тру-

бопровода.

6.1.7.3.

Случай транспорта

газа

из

одной точки в другую

помощью одного трубопро-

вода без изменения расхода

промежуточным

сжатием

Схема

обозначения представлены ниже. Учас-

ток

трубопровода

имеет диаметр

длину

Расход

газа

постоянен

по

всей длине. Полная

задача

расчета транспорта состоит

определении

диаметров участков, давлений всасывания

и на-

гнетания компрессорных станций

мест

их

распо-

ложения:

П+1

Qto

g^)

при следующих ограничениях

вводя:

РА-Р,(1),

РВ-Р

(л+1)

—

потери давления:

(/)-Рг(')

KL,Q

для всех/;

—

максимальное рабочее давление

трубопроводе

Р^/)

£ P.M.S. для

всех

/£ 2

или

еще

—

общая длина сети

п+1

Компрессорная станция

Участок 1

V!"S/

Участок

Давление

(1) Pi(2) P

(2) Р,{3)

Участок п + 1

Рг(п)

541

ТРАНСПОРТ ПО ТРУБОПРОВОДАМ

Решение

этой задачи позволяет сделать следу-

ющие

выводы:

— все участки трубопровода и в том числе 1 и "л"

имеют

одинаковый диаметр D;

— все компрессорные станции имеют одинаковое

давление нагнетания, равное максимальному

рабочему

(P.M.S.);

— все компрессорные станции находятся на оди-

наковом расстоянии друг от друга и, следова-

тельно, давление всасывания и степень сжатия

всех станций одинаковы;

— длина участка 1 не равна

нулю

(сжатие в нача-

ле),

если

только

ниже, чем давление всасы-

вания компрессорных станций.

В ходе разрешения проблемы находят отноше-

ние,

связывающее оптимальный диаметр с опти-

мальной степенью сжатия - г, так же как и отноше-

ние,

связывающее число станций со степенью сжа-

тия

газа

на станциях.

D =

5KAQV

tbc(P

-PB

=!^!

юг

.M.S.)

(P.M.s.)

f-L-i)

(1)

(2)

Система

уравнений (1) и (2) - неопределенное

уравнение, которое имеет одно неизвестное г, ес-

ли число л фиксировано. Полное решение состоит

в расчете г для различных величин и нахождении

и S(n). Оптимальное решение соответствует ве-

личине п, которое минимизирует S(n).

Расчетная величина D - это диаметр теоретиче-

ский.

Это ведет к необходимости

выбрать

один из

двух

ближайших стандартных диаметров и уточ-

нить

его в зависимости от степени сжатия компрес-

сорных

станций, т.е. к необходимости изучения не-

скольких вариантов. Эта типовая проблема хоро-

шо

иллюстрирует возможности и пределы

применения дифференциального метода, который

не

позволяет достичь полного решения

из-за

упро-

щения

рассматриваемого случая, но который

уменьшает число рассматриваемых вариантов.

6.1.7.4.

Газопровод без компремиро-

вания с расходом

газа

по пути

Проблема состоит в нахождении

длины

L единого

трубопровода диаметром D,, транспортирующего

расход Qf, эквивалентного с точки зрения потерь

давления ряда

"п"

участков длиной Ly и диаметром

Dy и транспортирующих расход Qy (т.е. подающего

расход Qy - Qy,.

в узле j); количество "п" отрезков

соответствует оптимуму с точки зрения капиталь-

ных вложений.

Задача

формулируется так:

— капитальные вложения в "rf участков

—- эквивалентные потери давления

-P'-KL^ = о.

Оптимизация капитальных вложений в зависи-

мости

от диаметров при наличии ограничений по-

терь давления может осуществляться с помощью

метода

множителей Лагранжа (приравнивание ну-

лю частной производной по D, от функции S + AF с

A,-const

const - С при любой/.

Откуда

2с

Q. I

. 1 /

L =

Приняв В/ -

\-Р?,

с/{с

Ъ)

имеем

следующий ре-

зультат. Оптимальная последовательность участ-

ков эквивалентна одному участку, который транс-

портировал бы расход Q

первого участка и длина

которого L будет такой, что коэффициент В равен

2e/(e+s>

или равен сумме коэффициентов В каж-

дого участка

этому

имеем:

p?-p?*i

fL,v<M7

•йй)й)

из уравнения для потерь давления

т.к.

—'— - С оптимум капвложений:

U-

Да,

2с

_ By

Qi-Q

-Q

Qn-i-Qn

Участок

Давление

Р,

Давление

Рг

Давление

Р„.,

Давление

Р„

Длина

Диаметр

Длина

Диаметр

ДлинаU

Диаметр

542

ТРАНСПОРТ ПО ТРУБОПРОВОДАМ

Это демонстрирует второй результат:

Для участков, расположенных последователь-

но,

оптимальная структура такова, что квадратич-

ные потери

давления

каждого участка пропорцио-

нальны

коэффициенту В, которые их характеризу-

ют.

6.1.7.5.

Трубопровод с расходом

газа

по

пути с

компремированием

в начале

Проблема решается заменой последовательно-

сти

участков одним эквивалентным участком в со-

ответствии с методикой в § 6.1.7.4. Затем по фор-

муле

§ 6.1.7.2 рассчитывают давление нагнетания

компрессора,

расположенного в

начале

эквива-

лентного участка.

Определяют серию диаметров

D,«

1/5

2с

=L,Q;

где:

Р,- давление нагнетания;

Р„-

давление в конце

сети.

6.1.7.6.

Разветвленная сеть

метод

Комбета

6.1.7.6.1.

Промежуточный результат

для сети в виде звезды

Рассмотрим

сначала

сеть, все участки которой

выходят

из одной точки и в конце которых давле-

ние одинаковое (идентичное):

Участок!

диаметром

длиной

транспортирует

расход

О/.

Находится один участок диаметром D и длиной L,

транспортирующий

расход Q = £Q

таким образом,

чтобы

давление в

начале

и конце

было

бы Р

и Р,

соответственно и так, что составляющая,

зави-

сящая от диаметра в капитальных вложениях,

была

бы равна сумме составляющих, зависящих от диа-

метра в капитальных вложениях каждого участка.

Эти два условия могут формулироваться также:

L = У Ь0%,

для всех/.

Откуда

1 +

2с „

i +

e 2с

= V L,

*Q7

« JU i I

У-1

Принимая А = L

•

C/S

отсюда находим следу-

ющий

третий результат:

число п участков в звезде, все концы которых

имеют такие же давление, падение

давления

и ка-

питальные

вложения (составляющая, независимая

от диаметра), как и один участок, коэффициент А

которого

равен сумме коэффициентов А каждого

отрезка.

Кроме

того,

А = L

(LQ

C+5

)

В (равенство 1).

6.1.7.6.2.

Метод

Комбета

Метод

Комбета применяется к

случаю

разветв-

ленной

сети,

имеющей один источник, известное

давление и одинаковое давление на конце всех

участков.

Сеть

состоит из участков, соединенных после-

довательно или звездой известной длины, транс-

портирующих известный расход, и на конце каждо-

го

может

быть

отбор

газа.

Проблема состоит в том,

чтобы

найти диаметр каждого участка таким обра-

зом,

чтобы

получить минимальные капитальные

вложения (т.е. капитальные вложения, зависящие

от диаметра, т.к. капитальные вложения, незави-

симые от диаметра, постоянны, независимы от

выбранного решения, известных длин участков).

Решение проблемы опирается на три результа-

та,

показанных в § 6.1.7.4 и

6.1.7.6.1.

Применяемая

Участок

вх<*|

Участок

„С

-Е

Каждый

участок

имеет

длину Ц и

диаметр

Df.

методика

может

быть

обобщена на основе просто-

го

примера, приведенного ниже.

Участок BDE, эквивалентный с точки зрения оп-

тимизации

капитальных вложений одного трубо-

543