Baumgarte T., Shapiro S. Numerical Relativity. Solving Einstein’s Equations on the Computer

Подождите немного. Документ загружается.

4.3 Harmonic coordinates and variations 111

be better to impose an alternative condition that drives K back to zero. We can accomplish

this task by employing the condition

∂

K =−cK, (4.35)

where c is some positive constant. Note that the above condition is completely consistent

with (4.11). Inserting the above relation into equation (4.9)wenowﬁnd

α = α



+ 4π(ρ + S)



+ β

K + cK, (4.36)

which is still an elliptic equation for the lapse α.

We now convert equation (4.36) into a parabolic equation by adding a “time” derivative

of the lapse,

∂

α = D

α − α



+ 4π(ρ + S)



− β

K − cK, (4.37)

where λ is some time parameter. Setting λ = t, we can convert this expression into

∂

α =  D

α − α



+ 4π(ρ + S)



− β

K − cK, (4.38)

where the parameter  now acts as an effective diffusion constant. We note that we can

write the new lapse condition (4.38) more compactly as

∂

α =−(∂

K + cK). (4.39)

This slicing condition is often referred to as a K-driver condition.

Equation (4.35), corresponding to the exponential decay of K to zero as time increases,

is the solution to equation (4.39)as →∞. However, setting  too large may produce a

numerical instability, since some numerical prescriptions for solving parabolic equations

must satisfy a Courant condition that limits the size of the allowed time step (see Chap-

ter 6.2.4). For sufﬁciently large , this time step may have to be chosen signiﬁcantly smaller

than the one used to evolve the gravitational ﬁeld equations. In this case equation (4.38)

or (4.39) can be solved by breaking up each evolution time step into several substeps. This

approach is equivalent to solving equation (4.36) by relaxation, except that the relaxation

process is not necessarily carried out to convergence, since it sufﬁces to impose maximal

slicing only approximately.

4.3 Harmonic coordinates and variations

Consider a contraction of the 4-dimensional connection coefﬁcients

(4)



≡ g

bc (4)



=−

|g|

1/2

∂



|g|

1/2



. (4.40)

See also Duez et al. (2003), who typically use ﬁve substeps per evolution time step, with  ≈ 0.6andc ≈ 0.1.

112 Chapter 4 Choosing coordinates: the lapse and shift

One way to impose a gauge condition is to set these quantities equal to some predetermined

gauge source functions H

(4)



= H

. (4.41)

In particular, we may choose these gauge source functions to vanish, which deﬁnes

harmonic coordinates

(4)



= 0. (4.42)

Exercise 4.8 explains why these coordinates are called “harmonic”.

Exercise 4.8 Show that in harmonic coordinates, the coordinates x

themselves are

harmonic functions,

∇

≡∇

∇

= 0. (4.43)

Inserting the metric (2.119) into equation (4.40) shows that in harmonic coordinates the

lapse and shift satisfy the coupled set of hyperbolic equations

(∂

− β

∂

) α =−α

K (4.44)

(∂

− β

∂

) β

=−α



∂

ln α + γ





. (4.45)

Exercise 4.9 Derive equations (4.44)and(4.45).

Harmonic coordinates have played an important role in the mathematical development of

general relativity, since they bring the 4-dimensional Ricci tensor

(4)

into a particularly

simple form.

Exercise 4.10 Show that in terms of

(4)



, the Ricci tensor

(4)

can be written

(4)

=−

∂

+ g

c(a

∂

(4)



(4)



c (4)



(ab)c

+2g

ed (4)



e(a

(4)



b)cd

+ g

cd (4)



(4)



ecb

. (4.46)

With the Ricci tensor expressed in terms of second derivatives of the metric (as in

equation 2.143), the second derivatives appear in four different terms with the free indices

appearing in all possible different positions. As demonstrated in exercise 4.10, three of these

four terms can be absorbed in the derivative of the connection coefﬁcients

(4)



, leaving

only one term that acts as a wave operator. In harmonic coordinates, where

(4)



= 0,

Einstein’s equations therefore reduce to a set of nonlinear wave equations,

which is

why all of the early hyperbolic formulations of Einstein’s equations are based on these

coordinates.

We will return to these considerations in Chapter 11.

See Smarr and York (1978b); Yo r k , J r . (1979).

De Donder (1921); Lanczos (1922).

E.g., Choquet-Bruhat (1952); Fischer and Marsden (1972).

4.3 Harmonic coordinates and variations 113

Completely harmonic coordinates have been adopted in only a few 3 + 1 simulations,

although a formalism based on “generalized harmonic coordinates”, has been employed

very successfully.

We will discuss this approach in much greater detail in Chapter 11.3.

Morecommonin3+ 1 calculations is harmonic slicing, in which only the time-component

(4)



is set to zero. Combining harmonic slicing with a zero shift yields a particularly simple

equation for the lapse,

∂

α =−α

K, (4.47)

which, after inserting equations (2.136)forα K , can be integrated to yield

α = C(x

)γ

1/2

. (4.48)

Here C(x

) is a constant of integration that may depend on the spatial coordinates x

but not on time. This condition is identical to keeping the densitized lapse ¯α = γ

−1/2

constant (see equation 3.100).

Exercise 4.11 Show that t = constant slices of the Schwarzschild spacetime in

isotropic coordinates (equations 2.145 through 2.148) are harmonic.

The harmonic slicing condition (4.48) is just about as simple as the geodesic slicing

condition (4.1), but it provides for a much more stable numerical evolution.

It does

not focus coordinate observers and in some cases has allowed for long time evolutions.

However, there is no guarantee that harmonic slicing will lead to well-behaved coordinates

in more general situations

and it has been pointed out that the singularity avoidance

properties of harmonic slicing are weaker than those, for example, of maximal slicing.

Equation (4.48) is an example of a coordinate condition in which the lapse can be found

algebraically, without having to solve complicated and computer-intensive differential

equations, as is necessary for maximal slicing. To generalize this condition, we can decorate

the right hand side of equation (4.47) with a positive but otherwise arbitrary function

f (α),

∂

α =−α

f (α)K . (4.49)

For f = 1 this condition obviously reduces to the harmonic slicing condition (4.47) above.

For f = 0(andα = 1 initially), it reduces to geodesic slicing (Section 4.1). Formally,

maximal slicing (Section 4.2) corresponds to f →∞.

For f = 2/α, the condition

See Landry and Teukolsky (1999); Garﬁnkle (2002).

See Pretorius (2005a,b).

Other time-independent harmonic slices of Schwarzschild and Kerr–Newman spacetimes for which the lapse does not

vanish on the horizon have been derived by Bona and Mass

o (1988)andCook and Scheel (1997).

See, e.g., Shibata and Nakamura (1995); Baumgarte and Shapiro (1998).

See Cook and Scheel (1997)andBaumgarte et al. (1999) for some examples.

See, e.g., Alcubierre (1997); Alcubierre and Mass

o (1998); Khokhlov and Novikov (2002).

Shibata and Nakamura (1995); Garﬁnkle (2002).

See Bona et al. (1995).

See exercise H.4 for an example.

114 Chapter 4 Choosing coordinates: the lapse and shift

(4.49) can be integrated to yield

α = 1 + ln γ, (4.50)

wherewehaveusedequation(2.136) and have chosen the constant of integration to be unity.

This quite popular slicing condition is often called “1+log” slicing. As an algebraic slicing

condition it has the virtue of being extremely simple to implement and fast to solve. It has

also been found to have stronger singularity avoidance properties than harmonic slicing.

The latter can be motivated by the observation that f becomes large when α becomes

small, so that it probably behaves more like maximal slicing than harmonic slicing.

In the above derivation we assumed β

= 0, which may or may not be a good choice.

Allowing for a nonzero shift, the condition (4.49) with f = 2/α may be generalized to

include an advective shift term,

(∂

− β

∂

)α =−2αK . (4.51)

Equation (4.51) deserves to be boxed, since it has proven to be an extremely successful and

robust (hyperbolic) slicing condition. It is currently adopted in in many “moving puncture”

binary black hole simulations. We will discuss these simulations, and the role of the slicing

condition (4.51), in much greater detail in Chapter 13.1.3.

Before proceeding we point out that the “advective” version of the 1+log condition,

equation (4.51), can be written as

∇

α = L

α =−2K. (4.52)

This means that this slicing condition is covariant in the sense that it does not depend

on the choice of the shift. The “nonadvective” version (4.49), on the other hand, is not

covariant, since the “direction” of the partial derivative ∂

α does depend on the shift. Stated

differently, the nonadvective derivative ∂

α takes a derivative in the direction of the time

vector t

, which is coordinate dependent, whereas the advective term −β

∂

α shifts the

direction back along the normal vector n

, which has a geometric, coordinate-independent

meaning.

4.4 Quasi-isotropic and radial gauge

In the previous sections we have focused primarily on time slicing conditions that specify

the lapse function α. We now turn to gauge conditions for the spatial coordinates, i.e., con-

ditions that specify the shift vector β

. As is the case when picking a lapse, an important

goal when choosing a shift is to provide for a stable, long-term dynamical evolution. In

addition, it is often desirable to bring the spatial metric into a simple form. For asymp-

totically ﬂat spacetimes, for example, one might like the metric at large distances to be

related straightforwardly to the Schwarzschild metric in some familiar coordinate system.

One might also like gravitational radiation to be easily identiﬁable as, for example, the

transverse-traceless components of an asymptotically ﬂat metric.

4.4 Quasi-isotropic and radial gauge 115

Loosely speaking, two different strategies can be employed when constructing a spatial

gauge condition. One strategy is to deﬁne a geometric condition on the spatial metric

from which a gauge condition can be derived. An example of such a condition is the

minimal distortion gauge, which we will discuss in Section 4.5. Alternatively, we can

impose an algebraic condition on the spatial metric directly. For example, we can set

some of its components to zero in order to simplify the Einstein equations. This latter

approach is the basis of the quasi-isotropic and radial gauge conditions, which we will

discuss in this section. Both of these gauges have played important roles in the evolution of

axisymmetric spacetimes. We shall assume that the spacetimes considered in this section

are axisymmetric and we will adopt spherical polar coordinates to treat them.

In general the spatial metric γ

has six independent components. Using our three degrees

of spatial coordinate freedom we can impose three conditions on the metric, and thereby

reduce the number of its independent variables to three. In spherical polar coordinates, the

quasi-isotropic gauge is deﬁned by the three conditions

rθ

= γ

rφ

= 0 (4.53)

and

θθ

φφ

− (γ

θφ

)

= γ

φφ

, (4.54)

which reduces the metric to the form

= A

(dr

dθ

) + B

(sin θdφ + ξ dθ)

. (4.55)

Demanding that conditions (4.53) and (4.54) hold at all times, we can insert them into the

evolution equation (2.134), and this results in a set of three coupled differential equations

for the three components of the shift β

Exercise 4.12 For axisymmetric spacetimes in the absence of net angular momen-

tum we can set ξ = 0andK

= 0. Argue that in this case the quasi-isotropic shift

satisﬁes β

= 0and

r∂





− ∂

= α(2K

+ K

), (4.56)

r∂

+ ∂





= 2α

. (4.57)

To introduce a somewhat more “natural” set of variables, we can replace A and B by

the conformal factor

= A

B (4.58)

and deﬁne a new variable,

η = ln(A/B), (4.59)

See, e.g., Smarr (1979b); Bardeen and Piran (1983); Evans (1984); Abrahams and Evans (1988); Shapiro and Teukolsky

(1992a); Abrahams et al. (1994).

116 Chapter 4 Choosing coordinates: the lapse and shift

which is a measure of the anisotropy of the spatial slices. The two variables η and ξ are

“dynamical” or “radiative” variables that serve to measure gravitational waves at large

distance from the gravitating source. We will explore some concrete examples that use

these variables in Chapter 10.

In terms of ψ, η and ξ, the line element (4.55)nowtakes

the form

= ψ



2η/3

(dr

dθ

) + e

−4η/3

(sin θdφ + ξ dθ)



. (4.60)

In spherical symmetry we can set, without loss of generality, η = ξ = 0, in which case

the spatial metric reduces to the familiar form ψ

. In vacuum we therefore recover the

Schwarzschild solution in isotropic coordinates, which explains the name “quasi-isotropic”

gauge.

A related coordinate condition is the radial gauge, for which condition (4.54) is replaced

by the relation

θθ

φφ

− (γ

θφ

)

= r

sin

θ, (4.61)

while conditions (4.53) remain unchanged. The spatial metric then takes the form

= A

+ B

−2

dθ

+ B

(sin θdφ + ξ dθ)

. (4.62)

Equations for the shift vector can again be derived from equation (2.134) by demanding

that conditions (4.53) and (4.61) hold at all times.

In spherical symmetry we can set B = 1andξ = 0 without loss of generality, in

which case the metric (4.62) takes the form of the Schwarzschild metric in Schwarzschild

coordinates (see equation 3.22). This result again suggests that natural dynamical variables

in the radial gauge are ξ and η.

Exercise 4.13 The radial gauge has been used quite often with polar slicing in

axisymmetry.

Polar slicing is deﬁned by

≡ K

+ K

= 0. (4.63)

Show that in spherical symmetry (for which β

= β

= 0) the radial gauge and

polar slicing conditions in vacuum imply β

= 0.

While both the quasi-isotropic and radial gauges have been used extensively for calcu-

lations in spherical symmetry and axisymmetry, they are particularly convenient only in

spherical polar coordinates. Such coordinates are natural for spherical and axisymmetric

spacetimes, but they suffer from coordinate singularities at r = 0 and along the symmetry

axis where θ = 0andθ = π. Most calculations in full 3 +1 dimensions have adopted

Cartesian coordinates, which do not have such singularities. In addition, given that in

spherical symmetry the radial gauge reduces to Schwarzschild coordinates, this gauge

See also Appendix F.

Bardeen and Piran (1983) take η = B

− 1 for the dynamical variable in place of equation (4.59).

See, e.g., Bardeen and Piran (1983); Shapiro and Teukolsky (1986).

4.5 Minimal distortion and variations 117

condition is susceptible quite generally to developing coordinate singularities near the

horizon of any black hole that may be present in the spacetime.

4.5 Minimal distortion and variations

In Chapter 3 we found that the conformally related metric ¯γ

has ﬁve independent func-

tions, two of which correspond to true dynamical degrees of freedom and three to coordinate

freedom. For a stable and accurate numerical evolution it is desirable to eliminate purely

coordinate-related ﬂuctuations in ¯γ

. To accomplish this, one may want to construct a

gauge condition that minimizes the time rate of change of the conformally related metric.

This gauge condition is called minimal distortion.

A related but recently less popular

gauge condition is minimal strain, which minimizes the time rate of change of the spatial

metric instead of the conformally related metric.

In Chapter 3.3 we introduced u

as the traceless part of the time derivative of the spatial

metric,

≡ γ

1/3

∂

(γ

−1/3

), (4.64)

(see equation 3.92). Since u

is traceless, we can decompose it into a transverse-traceless

and a longitudinal part

= u

+ u

, (4.65)

similar to the decomposition of the traceless part of the extrinsic curvature in Chapter 3.2.

The divergence of the transverse part vanishes,

= 0, (4.66)

and the longitudinal part can we written as the vector gradient of a vector X

= D

+ D

−

= (LX)

. (4.67)

Since ¯γ

= γ

−1/3

is a vector density of weight −2/3, the right hand side of (4.67) can

be identiﬁed with the Lie derivative of ¯γ

along the vector X

= γ

1/3

¯γ

(4.68)

(see exercise A.10 in Appendix A). Evidently, the longitudinal part can be interpreted as

arising from a change of coordinates, generated by X

. It represents the coordinate effects

in the time development, which can therefore be eliminated by choosing u

to vanish. This

leaves only the transverse part u

, which implies that the divergence of u

itself must

vanish

= 0. (4.69)

See Smarr and York (1978a,b), whose derivation we will follow closely.

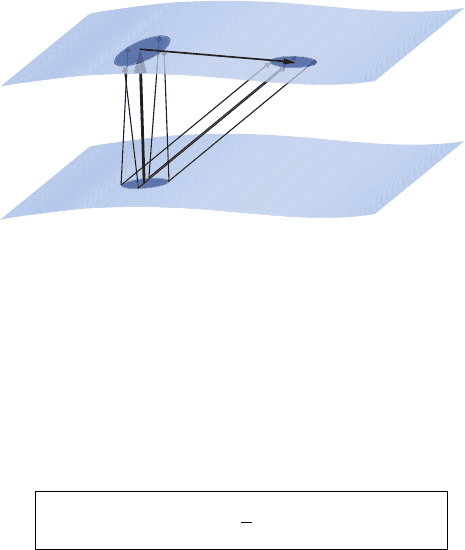
118 Chapter 4 Choosing coordinates: the lapse and shift

Figure 4.3 Schematic illustration of mimimal distortion, where the shift vector is chosen so that it minimizes

coordinate shear in the metric. If a sphere is transported from one time slice at t to a neighboring slice at t + dt

along the normal vector, it typically will be sheared into an ellipse. By adopting a minimal distortion shift vector,

some of the shear can be eliminated, depending on the spacetime geometry and the choice of time coordinate.

[After Smarr and York (1978a).]

Combining this with equation (3.99) yields

(Lβ)

= 2D

(α A

) (4.70)

(

β)

= 2A

α +

αγ

K + 16παS

, (4.71)

where we have replaced the divergence of A

with the momentum constraint, equa-

tion (3.38).

Equation (4.71)istheminimal distortion condition for the shift vector

. The geometric interpretation of minimal distortion is elucidated in exercise 4.14 and

Figure 4.3. The quantity u

can be viewed as a “distortion tensor” that measures the change

in the shape (but not the size) of a small spheroid as it evolves from one time slice to a neigh-

boring one. It is analogous to the shear strain instrinsic to a thin shell as it is deformed.

Exercise 4.14 Derive the minimal distortion condition (4.71) by varying the action

A ≡



1/2

x (4.72)

with respect to β

, keeping the boundary ﬁxed, and requiring δA = 0. Note that A

it is a nonnegative global measure of the magnitude of the time rate of change of

the conformal metric. The quantity u

is analogous to the energy density and the

integral

A to the total shear stretching energy of a deformed thin shell. Taking a

second variation with respect to β

shows that equation (4.71) minimizes A.

Hint: Substitute equation (3.93) into equation (4.72).

It is also useful to express equation (4.71) in terms of conformally related quantities.

Using (Lβ)

= ψ

−4

(

Lβ)

and D

= ψ

−10

(ψ

) for any symmetric, traceless

Equation (4.71) also follows from equation (3.102), using equation (4.69).

Yo r k , J r . (1979).

4.5 Minimal distortion and variations 119

tensor, we ﬁnd

(

β)

= ψ

−4



(



β)

+ (

Lβ)

ln ψ



, (4.73)

and hence

(



β)

+ (

Lβ)

ln ψ

= 2ψ

−6

α +

α ¯γ

K + 16πψ

αS

. (4.74)

Exercise 4.15 Adopt the conformal scaling relation of equation (3.97), u

= ψ

and show that condition (4.69) is equivalent to the relation

(ψ

) = 0. (4.75)

Then derive equation (4.74) directly from equation (4.75).

The relation between the shift condition that we found in the context of the conformal

thin-sandwich formalism (see Chapter 3.3) and the minimal distortion shift is explored in

exercise 4.16.

Exercise 4.16 Derive the minimal distortion shift condition (4.74) by starting with

the momentum constraint as expressed by equation (3.102). Adopt equation (4.75)

and use equation (3.101) to eliminate

The minimal distortion condition (4.74) is a set of coupled elliptic equations for the

components of the shift vector. In higher dimensions, it requires appreciable computational

resources to solve such a system numerically. But just as we discussed in Section 4.2 for the

case of maximal slicing, it is reasonable to expect that an “approximate minimal distortion”

condition may lead to a coordinate system with similar geometric properties. One possible

simpliﬁcation lies in replacing the covariant derivative operators in equation (4.74) with

the corresponding ﬂat space operators.

The operators then become ordinary partial

derivatives in Cartesian coordinates, which simpliﬁes the form of the equations and reduces

the computational effort required to solve them.

A related spatial gauge condition is based on the “connection functions”



≡ ¯γ



(4.76)

that we shall introduce in Chapter 11.5 in connection with the BSSN formulation of the

3 + 1 equations. The BSSN formulation also assumes that ¯γ = det( ¯γ

) = 1 in Cartesian

coordinates, so that



=−∂

¯γ

. (4.77)

In Section 4.3 we introduced their 4-dimensional counterparts (4.40) which we set to zero

to deﬁne harmonic coordinates. In complete analogy we could now set the connection

Shibata (1999b).

120 Chapter 4 Choosing coordinates: the lapse and shift

functions



to deﬁne “conformal three-harmonic” coordinates. Alternatively, consider

setting their time derivative to zero

∂



= 0. (4.78)

We can compute the time derivative of the connection functions by combining equa-

tion (4.77) with the evolution equation for the spatial metric, equation (2.134). Insert-

ing the result (see equation 11.43) into equation (4.78) then yields the Gamma-freezing

condition

¯γ

∂

¯γ

, jl

+ β

∂



−



∂



∂

= 2

∂

α − 2α





−

¯γ

∂

K − ¯γ

+ 6

∂

ln ψ



(4.79)

Here we have used the rescaling law

= ψ

, (4.80)

that is used more commonly in the context of the BSSN formulation than the law (3.35)

that we employed earlier. To distinguish the two rescaling laws we use a tilde instead of

a bar in equations (4.79) and (4.80). The relation to minimal distortion can be seen by

combining equations (4.78), (4.77) and (3.94), which yields

∂

(

) = 0. (4.81)

Exercise 4.17 Derive equation (4.81).

Equation (4.81) can now be compared to the corresponding divergence criterion (4.75)

for minimal distortion.

The condition (4.79) forms a complicated set of coupled elliptic equations for the

components of the shift vector. In analogy to our conversion of maximal slicing into

a parabolic evolution equation via the K-driver condition (4.39), we can convert these

elliptic equations for the shift into parabolic evolution equations by approximating the

Gamma freezing condition (4.78) with the Gamma-driver,

∂

= k(∂



+ η



), (4.82)

where k and η are positive constants. Inserting equation (11.43)for∂



results in a

parabolic equation for β

, in complete analogy to the K-driver condition (4.38) for the

lapse. We can go a step further and construct a hyperbolic Gamma-driver as follows

∂

= ∂



− ηB

(4.83)

Alcubierre and Br

ugmann (2001).

See Alcubierre and Br

ugmann (2001); Duez et al. (2003).

Campanelli et al. (2006).