Baumgarte T., Shapiro S. Numerical Relativity. Solving Einstein’s Equations on the Computer

Подождите немного. Документ загружается.

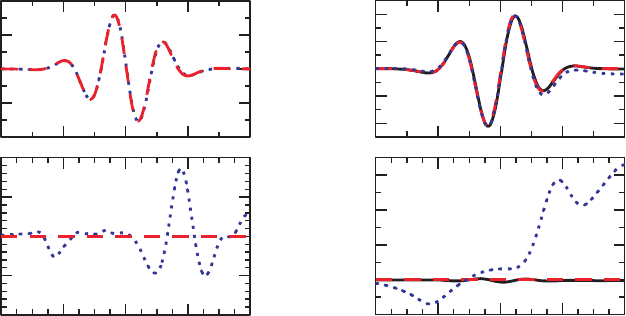
9.4 Extracting gravitational waveforms 351

0.008

0.001

0.004

0.0005

−0.004

−0.0005

−0.001

−0.008

Im(y

)

Re(y

)

−0.0001

−5×10

−5

−2×10

−5

−4

−2

0.0001

t − r

5×10

−5

6×10

−5

4×10

−5

2×10

−5

Figure 9.8 The left panels show the Weyl scalar ψ

for an even-parity l = 2, m = 0 linearized wave at a point

(r,θ,φ) = (6.0, 0.79, 0.52). The dotted (blue) line shows numerical results, and the dashed (red) line analytical

values. The right panels show the gravitational waveforms h

and h

for the same wave. The dashed (red) lines

show the analytical waveforms (which are computed in exercise 9.8), the solid (black) lines are the numerical

waveforms based on the Moncrief formalism (computed from R

, shown in Figure 9.7, using equation 9.109),

and the dotted (blue) line shows the numerical waveforms constructed from the Weyl scalar ψ

equation (9.126).

is that the Moncrief formalism requires taking only a ﬁrst derivative of the metric (in

equations 9.88 and 9.89 for the even-parity modes, or equation 9.101 for the odd-parity

modes) to ﬁnd the Moncrief functions, and only one integration (in equation 9.108)to

reconstruct the gravitational waveforms. In the Newman–Penrose formalism, by contrast,

we need second derivatives of the metric to compute ψ

(which are hidden in the Weyl

tensor

(4)

abcd

in equation 9.121), and then two integrations (in equation 9.126) to compute

and h

. Not surprisingly, the additional derivative and integration introduce additional

numerical error.

Another difference in our particular calculation is that we computed the Moncrief

quantities from their modes, and the Newman–Penrose quantities locally, without doing a

modal decomposition. Computing the modes involves surface integrals, which effectively

ﬁlters out some of the numerical noise present in the higher-order modes. Many applications

that employ the Newman–Penrose formalism therefore also compute the modes (9.134)

and then reconstruct ψ

locally from the decomposition (9.133). This procedure yields

more accurate results, at least for the dominant, lowest-order modes.

Collapse of collisionless

clusters in axisymmetry

As we learned in Chapter 8, where we studied spherical systems, collisionless clusters

provide a simple relativistic source for exploring the nature of Einstein’s equations and

experimenting with numerical techniques to solve them. Once we relax the restriction

to spherical symmetry, the spacetimes can exhibit two new dynamical features: rotation

and gravitational waves. Not much is known about nonspherical collisionless systems in

general relativity, even for stationary equilibria. Some interesting results have emerged

by exploiting numerical relativity to investigate the equilibrium structure and collapse of

nonspherical rotating and nonrotating clusters in axisymmetry.

To highlight the power of

the technique, we shall summarize a few of the simulations and their key ﬁndings in this

chapter.

The examples discussed below are chosen to demonstrate how numerical relativity, quite

apart from providing accurate quantitative solutions to dynamical scenarios involving

strong gravitational ﬁelds, can provide qualitative insight into Einstein’s equations in

those cases where uncertainty still prevails. It can even be helpful as a guide to proving

(or disproving) theorems about strong-ﬁeld spacetimes in those instances where analytic

means alone have not been adequate.

10.1 Collapse of prolate spheroids to spindle singularities

It is well-known that classical general relativity admits solutions with singularities, and that

such solutions can be produced by the gravitational collapse of nonsingular, asymptotically

ﬂat initial data. The Cosmic Censorship Conjecture of Penrose

states that such singularities

will always be clothed by event horizons and hence can never be visible from the outside (no

naked singularities). If cosmic censorship holds, then there is no problem with predicting

the future evolution outside the event horizon. If it does not hold, then the formation of a

naked singularity during collapse would pose a dilemma for general relativity theory. In this

situation, one cannot say anything precise about the future evolution of any region of space

For calculations of nonspherical equilibrium clusters see, e.g., Shapiro and Teukolsky (1993a,b). For the collapse of

nonrotating clusters, see, e.g., Shapiro and Teukolsky (1991a,b), and for a review and additional references, Shapiro

and Teukolsky (1992a); see also Abrahams et al. (1994, 1995). For collapse of rotating clusters, see, e.g., Shapiro and

Teukolsky (1992a); Abrahams et al. (1994); Hughes et al. (1994); Shapiro et al. (1995).

Penrose (1969).

352

10.1 Collapse of prolate spheroids to spindle singularities 353

containing the singularity since new information could emerge from it in a completely

arbitrary way.

No deﬁnitive theorems guarantee that an event horizon always emerges to clothe a

singularity. Proving the validity of cosmic censorship remains one of the most outstanding

problems in the theory of general relativity.

Counter-examples have all been restricted to

spherical symmetry and typically involve shell crossing, shell focusing, or self-similarity.

We also discussed in Chapter 8.4 how scalar ﬁeld collapse in spherical symmetry generates

a critical solution that produces a naked singularity. A key issue is whether such singularities

are accidents of spherical symmetry.

In the absence of general theorems, and prior to simulations of nonspherical collapse,

Thorne

proposed the hoop conjecture: Black holes with horizons form when and only

when a mass M (= M

ADM

) gets compacted into a region whose proper circumference in

every direction is

∼

4π M. If the hoop conjecture is correct, aspherical collapse with one

or two dimensions appreciably larger than the others might lead to naked singularities.

That such a scenario is at all possible is suggested by the Lin–Mestel–Shu instabil-

ity, which concerns the collapse of a nonrotating, homogeneous spheroid of collisionless

matter in Newtonian gravity.

Such a conﬁguration remains homogeneous and spheroidal

throughout collapse. However, if the spheroid is slightly oblate at the onset, the conﬁg-

uration ultimately collapses to a ﬂat pancake, while if the spheroid is slightly prolate,

it collapses to an inﬁnitesimally thin spindle. While in both cases the density becomes

inﬁnite, the formation of a spindle during prolate collapse is particularly severe. The grav-

itational potential, gravitational force, tidal force, kinetic and potential energies all blow

up to inﬁnity in this case.

Might the Lin–Mestel–Shu instability in Newtonian gravitation have relevance to gen-

eral relativity? In general relativity it is known that inﬁnite cylinders do collapse to line

singularities which, in accord with the hoop conjecture, are not hidden by event horizons.

Of course, these conﬁgurations are not asymptotically ﬂat, hence they do not qualify as

counterexamples to cosmic censorhip. But what about conﬁgurations of ﬁnite size?

Shapiro and Teukolsky (1991a,b) explored this question by employing a mean-ﬁeld,

particle simulation scheme to solve Einstein’s equations for the evolution of nonrotating,

collisionless matter in axisymmetric spacetimes.

Their 2 + 1 axisymmetric scheme is an

extension of their 1 + 1 spherical code described in Chapter 8.2.

The code was tailored

to handle cases in which collisionless matter could collapse to a singularity, as in oblate

collapse to a ﬂat pancake or prolate collapse to a thin spindle.

See Berger (2002) for a discussion and references.

Thorne (1972); see also Misner et al. (1973), p. 867.

Lin et al. (1965).

Thorne (1972).

See Shapiro and Teukolsky (1991a) for a popular discussion.

For the Newtonian version of this scheme in axisymmetry, with applications, see Shapiro and Teukolsky (1987).

354 Chapter 10 Collapse of collisionless clusters in axisymmetry

The metric is written in the form

=−α

+ A

(dr + β

dt)

+ A

(dθ + β

dt)

+ B

sin

θdφ

. (10.1)

The full set of gravitational ﬁeld and matter equations is listed in Appendix F.The

code is fully constrained. Maximal slicing and quasi-isotropic spatial coordinates were

adopted as the gauge choices. A large battery of test-bed calculations were performed

to ensure the reliability of the code. These tests included the propagation of linearized

analytic gravitational waves with and without matter sources and nonlinear Brill waves in

vacuum spacetimes;

maintaining equilibria and identifying the point of onset of radial

instability for spherical equilibrium clusters; reproducing Oppenheimer–Snyder collapse

of homogeneous dust spheres and the collapse of homogeneous Newtonian spheroids in

the weak-ﬁeld limit.

A number of geometric probes were constructed to diagnose the

evolving spacetime. For example, the total mass and outgoing radiation energy ﬂux were

calculated to monitor mass-energy conservation. To conﬁrm the formation of a black

hole, the spacetime was probed for the appearance of an apparent horizon

and its area

and shape were computed when it is present. To assess the growth of a singularity, the

Riemann invariant I ≡

(4)

abcd

(4)

abcd

, which measures the strength of the gravitational

tidal ﬁeld, was computed at every spatial grid point. To test the hoop conjecture, the

minimum equatorial and polar circumferences outside the matter were determined.

Typical simulations were performed in equatorial symmetry with a spatial grid of 100

radial and 32 angular zones, and with 6000 test particles. A key adaptive grid feature that

enabled the simulations to snuggle close to singularities was that the angular grid was

allowed to fan and the radial grid was allowed to contract to follow the matter. In addition,

the particles were permitted to move on larger time steps than the ﬁeld variables, which

were restricted by the Courant condition. In particular, the particles were only advanced on

a time step comparable to the local dynamical time scale, as in equation (8.64). They were

thus held frozen until the ﬁeld variables caught up after being advanced every Courant

time step (see, e.g., equation 6.72, with v = c = 1).

The code was utilized to track the collapse of nonrotating relativistic prolate and oblate

spheroids of various initial sizes and eccentricities. The matter particles comprising the

spheroids were taken to be instantaneously at rest at t = 0. The technique adopted for

constructing exact, time-symmetric prolate spheroids

is given in exercise 10.1.Inthe

Newtonian limit, these initial conﬁgurations reduce to homogeneous spheroids, but rela-

tivistic conﬁgurations are inhomogeneous with density increasing outwards. Given a den-

sity proﬁle, particles are distributed to sample the initial phase-space distribution function.

When the spheroids are large (size  M in all directions) the code correctly tracks the

Newtonian solutions.

Brill waves are gravitational waves resulting from time-symmetric initial data in axisymmetric, vacuum spacetimes;

see exercise 3.5. See also Eppley (1977) for numerical evolutions of Brill waves.

Lin et al. (1965); Shapiro and Teukolsky (1987).

See Chapter 7.3.

Nakamura et al. (1988).

10.1 Collapse of prolate spheroids to spindle singularities 355

Exercise 10.1 For a homogeneous spheroid in Newtonian gravitation, Poisson’s

equation ∇



= 4πρ

relates the potential 

to the rest-mass density ρ

where







4πa

c/3

, R

+ z

≤ 1,

0, elsewhere.

(10.2)

Here M

is the total Newtonian rest mass, a is the equatorial radius, c is the polar

radius and R and z are cylindrical coordinates. The solution for the potential is well-

known, but is not needed for this exercise. The resulting Newtonian gravitational

binding energy for a prolate spheroid of eccentricity e = (1 − a

)

1/2

is given by

=−





x =

1 + e

1 − e

. (10.3)

(a) Consider a homogeneous spheroid of collisionless particles momentarily at rest

in general relativity. To try and minimize the initial radiation content of the space-

time, choose a conformally ﬂat spatial metric γ

= ψ

(i.e., A = B = ψ

equation 10.1) and argue that the only nontrivial equation that the initial data must

satisfy is the Hamiltonian constraint

(3)

R = 16πρ,whereρ = T

is the mass

density (= rest-mass density in this case), T

is the stress-energy tensor for colli-

sionless matter and n

is the normal vector to the initial t = 0 hypersurface. Show

the constraint condition reduces to

∇

ψ =−2πψ

ρ, (10.4)

with the boundary conditions

∇ψ = 0, at r = 0,ψ→ 1 +

, as r →∞, (10.5)

where M = M

ADM

is the total mass-energy of the conﬁguration.

(b) Choose the density proﬁle ρ according to 2πψ

ρ ≡ 4πρ

, for which the solution

to equation (10.4) is immediately given by ψ = 1 − 

. The density ρ is therefore

inhomogeneous, increases outward from the center, and is constant on self-similar

coordinate spheroidal surfaces. From this conclude that the total rest-mass energy

of the spheroid is

= 2M

+ 4W

, (10.6)

and the total mass-energy is

M = 2M

1 + (1 + αM

)

1/2

, (10.7)

where, for a prolate spheroid,

α =

5ce

1 + e

1 − e

. (10.8)

(4)

abcd (4)

abcd

= R

ijkl

in Cartesian

coordinates to ﬁnd

I = 96ψ

−12



∂

ψ∂



− 96ψ

−11

∂

ψ∂

ψ + ψ

−10

∂

ψ∂

∂

ψ.

(10.9)

356 Chapter 10 Collapse of collisionless clusters in axisymmetry

Evaluating equation (10.9) reveals

that as e → 1, prolate conﬁgurations form spindle

singularities located just outside the matter on the axis. When the spheroids are sufﬁciently

compact (

∼

M in all of its spatial dimensions) solving equation (7.51) shows that there is an

apparent horizon; otherwise there is none. A sequence of these momentary static prolate

spheroids of ﬁxed rest mass, but increasing eccentricity, foreshadows the evolutionary

collapse sequence of Shapiro and Teukolsky (1991b) that we shall now describe.

The left panels of Figure 10.1 show the fate of a typical, highly compact prolate conﬁgu-

ration; such a conﬁguration always collapses to a black hole. To appreciate the scale, recall

that in isotropic coordinates a Schwarzschild black hole on the initial time slice would have

aradiusr = 0.5M, corresponding to a Schwarzschild radius r

= 2M. The right panels

in Figure 10.1 depict the outcome of prolate collapse with the same initial eccentricity but

from a larger semi-major axis. Here the conﬁguration collapses to a spindle singularity

at the pole without the appearance of an apparent horizon. A search for either a single

global horizon centered on the origin, or a small disjoint horizon around the singularity

in each hemisphere, comes up empty. The spindle consists of a concentration of matter

near the axis in the vicinity of r ≈ 5M. Figure 10.2 shows the growth of the Riemann

invariant I at r = 6.1M on the axis, just outside the matter.

Prior to the formation of the

singularity, the typical size of I at any exterior radius r on the axis is ∼ M

 1.

With the formation of the spindle singularity, the value of I rises without bound in the

region near the pole. The maximum value of I determined numerically is limited only by

the resolution of the angular grid: the better the spindle is resolved, the larger the measured

value of I before the singularity causes the code (and possibly the spacetime!) to break

down. Unlike shell-crossing singularities, where I blows up in the matter interior whenever

the matter density is momentarily inﬁnite, the spindle singularity also extends outside the

matter beyond the pole at r = 5.8M (Figure 10.3). In fact, the peak value of I occurs in

the vacuum at r ≈ 6.1M.Heretheexterior tidal gravitational ﬁeld is blowing up, which is

not the case for shell crossing.

Probing the spacetime in the vicinity of the singularity suggests that it is is not a point,

but rather an extended region which, while including the matter spindle, grows most

rapidly in the vacuum exterior above the pole. The local geometry near the spindle exhibits

behavior similar to the late-time geometry near the axis along which a naked singularity

forms following the collapse of an inﬁnite cylinder. The spatial metric components grow

slowly with time, rising to a maximum of A ≈ B ≈ 1.7. The maximum occurs near the

origin and is only moderately larger than one, the value at large distance from the spheroid.

However, the tidal-ﬁeld invariant I , which depends on second derivatives of the metric,

diverges much more rapidly. This behavior mimics the logarithmic divergence of the metric

found along an analytic, prolate sequence of momentary static conﬁgurations of increasing

Nakamura et al. (1988).

The calculation of I during a 3 +1 simulation is simpliﬁed by decomposing it into spatial ﬁeld and matter variables

on each time slice; see Yo r k (1989), equation (109).

Recall that in Schwarzschild geometry, I = 48M

,wherer

is the Schwarzschild areal radius.

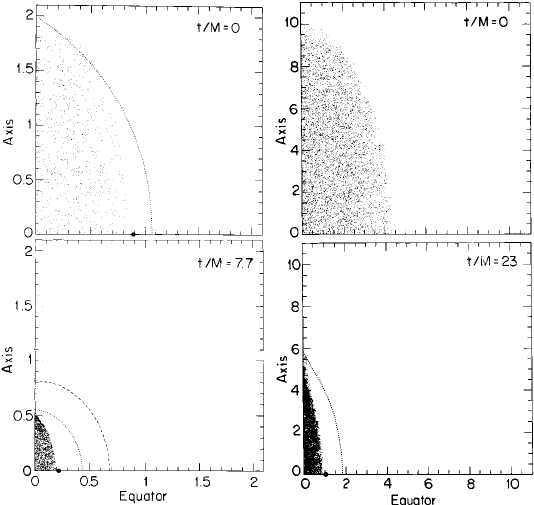
10.1 Collapse of prolate spheroids to spindle singularities 357

Figure 10.1 Left panels. Snapshots of the particle positions at initial and late times for prolate collapse. The

positions (in units of M) are projected onto a meridional plane. Initially the semi-major axis of the spheroid is

2M and the eccentricity is 0.9. The collapse proceeds nonhomologously and terminates with the formation of a

spindle singularity on the axis. However, an apparent horizon (marked by the dashed line) forms to cover the

singularity. At t/M = 7.7 its area is

A/16π M

= 0.98, close to the expected value of unity (gravitational

radiation losses are negligible). Its polar and equatorial circumferences at that time are

pole

/4π M = 1.03 and

/4π M = 0.91, at later times these circumferences become equal and approach the expected value of unity.

The minimum exterior polar circumference is shown by a dotted line and does not coincide with the matter

surface. Likewise, the minimum equatorial circumference, which is a circle, is indicated by a solid dot. Here

min

/4π M = 0.59 and C

min

pole

/4π M = 0.99. The formation of a black hole here is thus consistent with the hoop

conjecture. Right panels. Snapshots of the particle positions at the initial and ﬁnal times for prolate collapse with

the same initial eccentricity as in the left panel but with initial semi-major axis equal to 10M. The collapse

proceeds as in the left panel and terminates with the formation of a spindle singularity on the axis at

t/M = 23. The minimum polar circumference is

min

pole

/4π M = 2.8. There is no apparent horizon, in

agreement with the hoop conjecture. This may be a candidate for a naked singularity. [From Shapiro and

Teukolsky (1991b).]

eccentricity.

Of course, any such description of the singular region and the metric depends

on the time slicing and may be different for other choices of time coordinate. In principle

the spindle singularity might ﬁrst occur at the center rather than the pole with a different

time slicing.

See exercise 10.1.

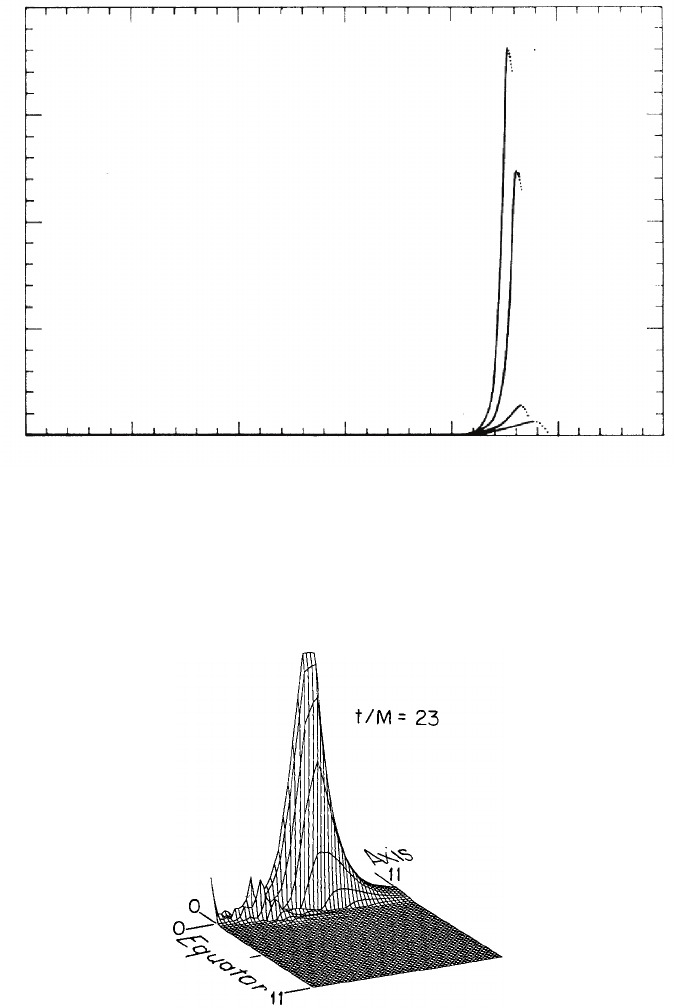
358 Chapter 10 Collapse of collisionless clusters in axisymmetry

0 5 10 15 20 25 30

t/ M

Figure 10.2 Growth of the Riemann invariant I (in units of M

−4

) vs. time for the collapse shown in the right

panels of Figure 10.1. The simulation was repeated with various angular grid resolutions. Each curve is labeled

by the number of angular zones used to cover one hemisphere. Dots indicate where the singularity has caused the

code to become inaccurate. [From Shapiro and Teukolsky (1991b).]

Figure 10.3 Proﬁle of I in a meridional plane for the collapse shown in the right panels of Figure 10.1.Forthe

case shown here employing 32 angular zones to cover one hemisphere, the peak value of I is 24/M

and occurs

on the axis just outside the matter. [From Shapiro and Teukolsky (1991b).]

10.2 Head-on collision of two black holes 359

The key question is whether or not this spindle singularity is naked or not. The absence

of an apparent horizon does not necessarily imply the absence of a global event horizon,

although the converse is true. This point has been emphasized by showing

that even

Schwarzschild spacetime can be sliced with nonspherical slices that approach arbitrarily

close to the singularity without any trapped surfaces. Because such singularities cause

numerical integrations to terminate, one cannot map out a spacetime arbitrarily far into the

future, which would be necessary to completely rule out the formation of an event horizon.

It may be telling that in the case of collapse from an initially compact state, outward

null geodesics are always found to turn around near the singularity, as expected when the

singularity resides inside an event horizon. By contrast, for collapse from large radius,

outward null geodesics are still propagating freely away from the vicinity of the singularity

up to the time the integrations terminate. It remains an open question for future research

whether any time slicing can be found which will be more effective in snuggling up to the

singularity without actually hitting it. Such a slicing might enable one to conﬁrm whether

all outward null geodesics manage to propagate to large distances, thereby determining

whether or not the singularities arising from nonrotating, prolate collapse are truly naked.

Vacuum simulations of highly prolate, Brill-wave initial data may shed additional light

on the issue of prolate collapse in general relativity. Prolate initial wave packets can be

constructed without apparent horizons but with arbitrarily large curvatures.

What is the

fate of such conﬁgurations – black holes or naked singularities? The original attempt

evolve these data used a partially constrained, axisymmetric scheme that could not proceed

sufﬁciently long to settle the question, due to a lack of resolution on the compactiﬁed spatial

grid. Subsequently, however, a fully constrained scheme, which used a multigrid method

for the elliptic equations and ﬁxed mesh reﬁnement, was able to evolve the same initial

data for much longer.

The same gauge conditions employed by Shapiro and Teukolsky

(1991a,b) were used here, but the code was written in cylindrical, rather than spherical polar,

coordinates. The longer evolution ultimately revealed an apparent horizon, conﬁrming the

formation of a black hole rather than a naked singularity.

10.2 Head-on collision of two black holes

As we know from high energy physics, a good way to to probe the underlying ﬁeld theory

governing the interactions of a relativistic system is to perform a collision experiment.

This is the motivation behind the simulations we shall summarize in this section, where we

will consider the the head-on collision of two identical clusters of “collisionless” particles

Wald and Iyer (1991).

Abrahams et al. (1992).

Garﬁnkle and Duncan (2001).

Rinne (2008a).

But as pointed out by Garﬁnkle and Duncan (2001), highly prolate Brill waves tend to become less prolate during

collapse rather than more, in contrast to prolate collisionless matter spheroids. So the ﬁnal fates of the two systems

may be qualitatively different.

360 Chapter 10 Collapse of collisionless clusters in axisymmetry

in general relativity.

Recall that these particles are called “collisionless” because they

interact exclusively by gravity and hence obey the relativistic Vlasov equation. Such

particles could represent stars in a cluster, massive neutrinos, axions, or any other form

of collisionless matter. Simulations of head-on collisions have been performed for several

nonrotating, initial conﬁgurations including: (1) a binary consisting of identical spheres of

particles, all momentarily at rest; (2) a binary of identical spheres of particles, where each

sphere is boosted towards each other; and (3) a binary of identical spheres of particles,

where the particles in each sphere are in randomly oriented, circular orbits about their

respective centers. In the ﬁrst two cases, the particles in the two spheres implode towards

their respective centers before colliding and form two, well-separated, black holes. Such

scenarios have been very useful for studying the head-on collision of binary black holes.

In the third case, each cluster is constructed to be in near-equilibrium initially, so it

does not implode prior to merger. Their collision from rest leads either to coalescence

and virialization to a new equilibrium conﬁguration, or to collapse to a black hole. This

third collision scenario is the collisionless analog of colliding neutron stars in relativistic

hydrodynamics.

Exercise 10.2 Consider the following quantity as a diagnostic of virial equilibrium

in a particle simulation,

=−



(1 + u

), (10.10)

where u

is the 4-velocity of the jth particle and the sum is over all the particles.

(a) Why does E

become constant in time in virial equilibrium?

(b) What is the meaning of E

in the Newtonian limit?

equilibrium has been achieved?

Hint: Consider various mass measures of the conﬁguration.

Shapiro and Teukolsky (1992b) used the same mean-ﬁeld particle simulation scheme

discussed in Section 10.1 and summarized in Appendix F to tackle these scenarios. This

scheme adopts the same form of the metric and gauge conditions as before and handles

general nonrotating, axisymmetric spacetimes containing collisionless matter. The simu-

lations took the system center of mass in each case to reside in the equatorial plane and

then exploited symmetry across the equator. The simulations then employed approximately

250 radial zones and 32 angular zones to cover the spatial grid in the upper hemisphere.

The initial data for the two spheres was constructed from prescriptions similar to the one

described in exercise 10.1 for single spheroids. The approach described in that exercise

was generalized to allow for binary systems, and modiﬁed to account for an initial velocity

boost in scenario two and for circular particle velocities in scenario three.

Shapiro and Teukolsky (1992b).