Baumgarte T., Shapiro S. Numerical Relativity. Solving Einstein’s Equations on the Computer

Подождите немного. Документ загружается.

16.3 Fully relativistic simulations 551

1.5

Γ = 2.00

(M/R)

∞

(M/R)

∞

= 0.10

= 0.14

0.5

(t − z

obs

) / P

t=0

(t − z

obs

) / P

t=0

−0.5

−1

0.5

−0.5

−1

0.5

−0.5

−1

0.5

−0.5

−1

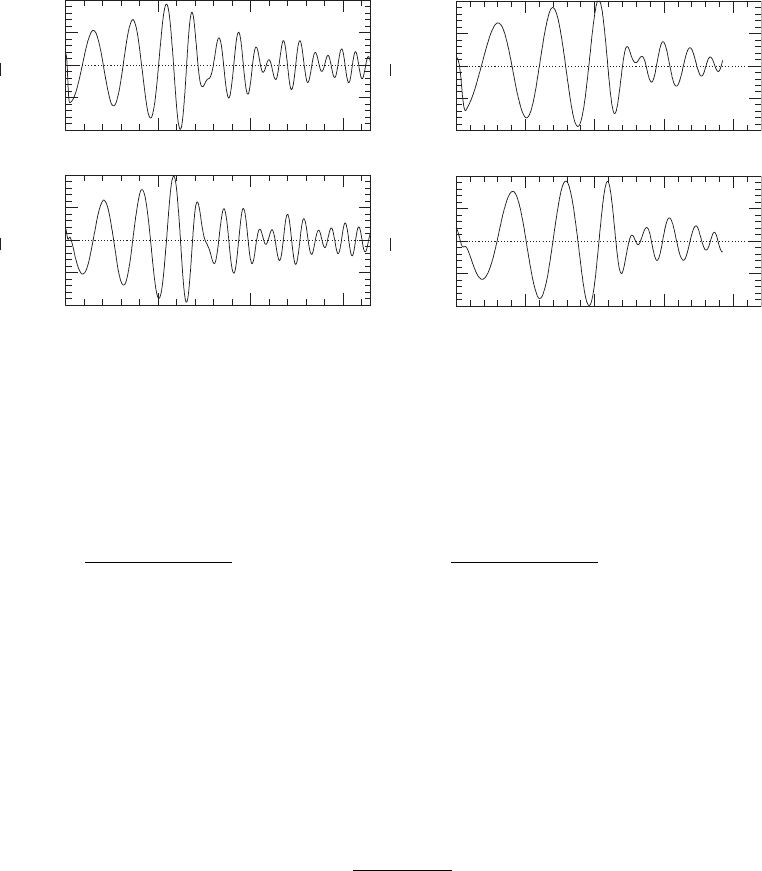
Figure 16.8 Gravitational wave amplitudes

and

as functions of retarded time for the n = 1 irrotational

binary neutron star models E and H of Shibata and Ury

u (2002). Model E (left panel) corresponds to a slightly

smaller mass then I1 and results in a differentially rotating hypermassive neutron star, while model H (right

panel) is similar to model I2 and results in a black hole. [From Shibata and Ury

u (2002).]

according to

≡

obs

ADM

(

M/R

)

∞



¯γ

− ¯γ



≡

obs

ADM

(

M/R

)

∞



¯γ



. (16.9)

Here z

obs

is the location of the observer. The quantities

and

calculated here are

expected to provide a reasonable approximation to the asymptotic gravitational waves, since

the adopted gauge condition is approximately transverse-traceless in the wave zone.

Note

that the wave amplitude attains its maximum along the z-axis, along which it is composed

only of |m|=2 modes.

Exercise 16.4 Show that at the point of contact of two equal-mass, spherical,

Newtonian stars in a circular binary, the quadrupole formula gives the amplitude of

gravitational waves along the z-axis to be

2M(M/R)

∞

obs

. (16.10)

This result explains the adopted normalization in equation (16.9).

The difference between the formation of a hypermassive remnant versus a black hole

immediately upon merger is reﬂected in their waveforms, as seen in Figure 16.8. Quasiperi-

odic oscillations are observed to persist for a long duration for the hypermassive remnant,

In the wave zone, the conformally related spatial metric used in equation (16.9) and the physical spatial metric are

nearly equal.

552 Chapter 16 Binary neutron star evolution

while such oscillations last only for a short time scale in the case of a prompt black hole

formation.

Unequal-mass binaries

Following up these simulations, Shibata et al. (2003b) next considered the merger of binary

neutron stars of unequal mass. Here again they adopted a simple -law EOS with  = 2

to explore the effect of varying the mass ratio q between 0.85 and 1. This is an appropriate

range to consider, since the mass ratio for all the observed galactic binary neutron stars

for which each mass is determined accurately resides in the this range.

The numerical

implementation has been improved in these simulations, beginning with the hydrody-

namics, which is performed by means of an HRSC scheme. Also, the conﬁgurations are

followed beginning from the late inspiral phase through the merger phase; this “early start”

allows the transition from inspiral to plunge to be triggered more properly by gravita-

tional radiation reaction, rather than by an artiﬁcial initial angular momentum depletion.

A hyperbolic shift equation similar in spirit to the one given by equation (14.44)isusedto

replace the time-consuming elliptic AMD gauge condition. A typical spatial grid size of

633 × 633 × 317 zones is employed in these simulations.

A number of interesting results emerge from this study. If the total rest mass of the system

exceeds approximately 1.7 times the maximum allowed rest mass of a spherical neutron

star, a black hole forms promptly upon merger, independently of the mass ratio. Otherwise

a hypermassive neutron star forms. The disk mass around the black holes increases with

decreasing rest-mass ratios and with increasing neutron star compactness. The merger

process and the gravitational waveforms are sensitive to the rest-mass ratios, even in the

restricted range q = 0.85–1. For example, the maximum amplitude is smaller for models

with smaller mass ratios. This behavior is due to the enhanced role of tidal effects for

smaller mass ratios, causing tidal disruption at larger orbital separation.

Also, emission

in modes of odd values of m, which is absent in the case of equal-mass binaries due to

π-rotation symmetry, is not negligible for the merger of unequal-mass binaries, although

the amplitude of this radiation never exceeds 5% of the l = 2, m = 2 mode.

Binaries with realistic EOSs

Having succeeded in simulating binary neutron star mergers for simple polytropes and

-law EOSs, Shibata et al. (2005) proceeded to explore mergers with more realistic

EOSs. They constructed a convenient “hybrid” hot nuclear EOS consisting of two parts,

P = P

cold

+ P

. For the cold nuclear matter contribution P

cold

they used both the SLy

and

Stairs (2004).

This effect was reported earlier in Newtonian and post-Newtonian studies; see Rasio and Shapiro (1994); Faber and

Rasio (2000, 2002).

Douchin and Haensel (2001).

16.3 Fully relativistic simulations 553

FPS

nuclear EOSs, for which the maximum allowed ADM mass of an isolated spherical

neutron star is 2.04M



and 1.80M



, respectively.

For the thermal contribution P

, they

adopted the law P

= (

− 1)ρ



,whereρ

is the rest-mass density, and 

=  − 

cold

is the speciﬁc thermal energy density. To match the stiff behavior of the cold contribution,

they chose 

= 2, but also experimented with other values.

Exercise 16.5 Assuming that the stars are completely cold when they begin

their plunge towards each other, what physical effect causes them to acquire

nonzero thermal energy? Estimate the resulting characteristic gas temperature in the

gas.

Simulations were performed for binary systems with total ADM mass in the range

between 2.4M



and 2.8M



and with rest-mass ratios q is the range 0.9

∼

1. Uniform

grids with as many as 633 × 633 ×317 zones were employed. They found that when the

total ADM mass exceeds a threshold M

thr

, a black hole forms promptly after merger,

independently of mass ratio. Otherwise a differentially rotating hypermassive neutron star

remnant forms. The value of M

thr

is found to be approximately 2.7M



for SLy and 2.5M



for FPS, which is larger than the maximum spherical or uniformly rotating mass in each

case.

For binaries with total masses exceeding M

thr

, over 99% of the rest-mass forms a black

hole promptly on merger. The spin of the black hole falls in the range J/M

≈ 0.7–0.8,

not very different from the spins typically arising from the collapse of rapidly spinning

stars.

The quasinormal mode ringdown radiation of the hole will then be at a frequency

f ≈ 6.5–7(2.8M



/M) kHz, which, unfortunately, exceeds the frequency range of optimal

sensitivity of all current laser interferometers.

For M < M

thr

the binary results in a hypermassive remnant. In contrast to the remnants

governed by a pure  = 2 EOS, the hypermassive remnants formed here are characterized

by a large ellipticity, a consequence of their high spin and high effective adiabatic index.

A typical relativistic ellipsoidal remnant is shown in Figure 16.9.

The remnant shown here results from the merger of an irrotational binary consisting of

identical neutron stars, each of which has an ADM mass of 1.3M



in isolation. The matter

is governed by the SLy hybrid EOS. The simulation begins from a quasiequilibrium circular

orbit just beyond the ISCO; the initial orbital period is about 2 ms and the merger occurs

after about one orbit. As a result of its spin and high ellipticity, the hypermassive remnant

Pandharipande and Ravenhall (1989).

For comparison, a -law EOS of the form P = Kρ



with  = 2 has a maximum ADM mass of 1.72(K /1.6 ×

)

1/2



,whereK is given in cgs units. However, the radii of neutron stars with this -law EOS are considerably

larger than the radii given by the adopted realistic EOSs; see Shibata et al. (2005), Figure 2b.

See Chapter 14.2.

See Chapter 9.3.

Rapidly rotating, nonaxisymmetric quasiequilibria do not exist unless the adiabatic index is sufﬁciently high. In

Newtonian theory, a uniform rotating Jacobi-like ellipsoid exists only if 

∼

2.25 and T /|W |

∼

0.14; James (1964);

Tassoul (1978).

Such triaxial ellipsoids were ﬁrst seen in the Newtonian coalescence calculations of Rasio and Shapiro (1994).

554 Chapter 16 Binary neutron star evolution

10.138

0.3c

(

)

Y (km)

−10

−20

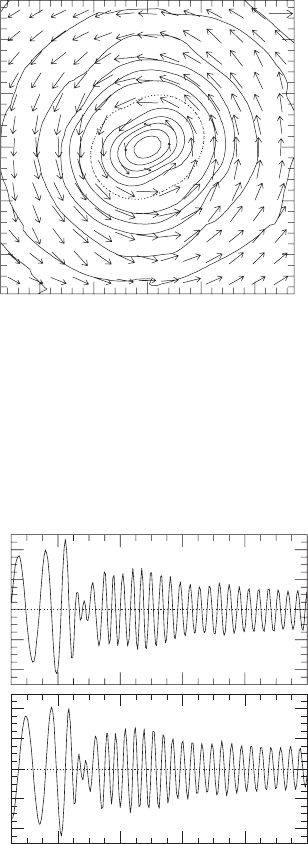
Figure 16.9 Contours of rest-mass density ρ

in the equatorial plane of an ellipsoidal hypermassive

remnant at time t = 10.138 ms. The simulation begins at t = 0 and merger occurs at t ∼ 2 ms. The solid

curves are drawn for contours deﬁned by ρ

= 2 × 10

× i g/cm

(i = 2,...,10) and for

2 ×10

× 10

−0.5i

g/cm

(i = 1,...,7). The dotted curve denotes the contour near nuclear density,

= 2 × 10

g/cm

. Vectors indicate the local velocity ﬁeld (v

), where the scale is shown in the upper

right-hand corner. [From Shibata (2005).]

246

ret

(ms)

810

4×10

−22

2×10

−22

−2×10

−22

2×10

−22

−2×10

−22

−4×10

−22

4×10

−22

−4×10

−22

Figure 16.10 Waveforms for the binary merger that produced the ellipsoidal hypermassive neutron star remnant

depicted in Figure 16.9. The observer is located along the rotational axis of the binary at a distance of 50 Mpc

and t

ret

is retarded time. [From Shibata (2005).]

is a strong emitter of quasiperiodic gravitational waves. The waveforms for the simulation

depicted in Figure 16.9 are shown in Figure 16.10. Their characteristic frequency is about

3 kHz and their amplitude is roughly 1.5 × 10

−22

(assuming a distance of 50 Mpc). These

features hold constant over many rotation periods since the emission damping time, about

50 ms, is very long.

16.3 Fully relativistic simulations 555

Exercise 16.6 Consider gravitational radiation emission in the quadrupole approx-

imation from a uniformly rotating, homogeneous, Newtonian ellipsoid.

(a) Show that the energy and angular momentum loss rates are given by





= 





=−



− I

)

, (16.11)

where I

= Ma

/5 are the components of the star’s quadrupole moment along the

principle axes in its equatorial plane, a

are the semimajor axes in the equatorial

plane, M is the mass, and  is the angular velocity, which points in the polar

direction.

(b) Show that the waveform amplitudes of the two polarization states are



− I

)cos(1 + cos

θ), (16.12)



− I

)sincosθ, (16.13)

where D is the distance to the source, θ is the angle between the rotation axis of

the star and line of sight from the Earth, and  ≡ 2



dt is twice the orbital

phase.

Gravitational radiation emitted by the nonaxisymmetric hypermassive remnant carries

off angular momentum. Since angular momentum is crucial in holding up the hypermas-

sive remnant against collapse, its dissipation by wave emission will eventually lead to a

“delayed” collapse to a rotating black hole. Unfortunately, the simulations performed here

were forced to terminate long before the collapse. The presence and ampliﬁcation of a

seed magnetic ﬁeld can accelerate the process, as demonstrated by simulations presented

in Chapter 14.2.5. Which mechanism dominates the dissipation of angular momentum

probably depends on the initial ﬁeld strength, the degree of differential rotation, the EOS,

the importance of other dissipative agents, like neutrino emission, and other factors. But

the ﬁnal fate – delayed collapse – is almost certain.

Shibata (2005) has pointed out that the quasiperiodic radiation from an ellipsoidal

remnant may be sufﬁciently strong for detection by advanced laser interferometers, even

though the frequency is near the high-end of their current dectability limit. The reason

is that a long-term integration over the many cycles of the wavetrain may increase the

effective peak amplitude above the noise level of detectors like Advanced LIGO. Also,

identifying the chirp signal from the binary during the inspiral phase prior to merger should

improve the search for a quasiperiodic signal from a hypermassive remnant. Detecting such

a quasiperiodic signal will then provide a lower limit to M

thr

, and will therefore constrain

the neutron star EOS. In fact, only a single detection of such a signal is necessary to

furnish a useful constraint. Since the theoretical values for M

thr

found from these binary

merger simulations are quite close to the total masses of the observed binary neutron stars

with accurate mass determinations, binary neutron star mergers leading to hypermassive

remnants might occur frequently.

556 Chapter 16 Binary neutron star evolution

0.7 0.8

0.0001

Disk mass (M )

0.001

0.01

SLy, M 2.76M

0.1

0.9 1

APR, M 2.96M

Figure 16.11 Baryon rest mass of the disk around the black hole as a function of the mass ratio Q

in the case

of prompt black hole formation. The disk mass is evaluated 0.5 ms after the appearance of an apparent horizon.

The open circles and squares denote the results with 633 ×633 × 317 zones for the APR and SLy EOSs,

respectively; the ﬁlled circles and squares denote the results with 377 × 377 ×189 zones. The results for the

APR and SLy EOSs are obtained for a total initial binary ADM mass of M ≈ 2.96M



and 2.76M



, respectively.

[From Shibata and Taniguchi (2006).]

Shibata and Taniguchi (2006) have extended some of these calculations in two areas.

First, they use a stiff cold nuclear EOS by Akmal et al. (1998) (APR) in place of FPS. This

choice was motivated by reports of the discovery of a heavy neutron star (pulsar) with a

mass of 2.1 ± 0.2M



Such measurement would establish a lower limit on the maximum

ADM mass of a spherical neutron star, and it is consistent with the APR maximum mass

(2.18M



), but not the FPS value. Their other motivation was to apply black hole excision

in cases of prompt black hole formation to evolve longer and thereby better determine the

ﬁnal state of the black hole system. In particular, they wanted to determine the ﬁnal mass

of the quasistationary disk surrounding the black hole. The disk is an important ingredient

in black hole models of the central engine of short-hard GRB sources, as we have noted in

Chapter 14.2.5. Finally, they wanted to simulate a wider range of mass ratios, 0.65

∼

Collecting their results, Shibata and Taniguchi (2006) conclude that the the value of M

thr

depends on the adopted cold nuclear EOS, but can be approximated by 1.3–1.35M

sph

,where

sph

is the maximum mass of a spherical neutron star constructed with the same EOS. Since

uniform rotation can account for mass increases of at most about 20%, differential rotation

is again required to support hypermassive neutron star remnants.

Shibata and Taniguchi

PSR J0751+1807; Nice et al. (2005). But note that more recent timing observations have led to a substantially lower

mass for this pulsar, 1.26 ± 0.14M



; Nice et al. (2008).

ThevalueofM

thr

sph

is thus smaller for stars constructed from realistic nuclear EOSs than for polytropes. This

result is consistent with the ﬁnding of Morrison et al. (2004) that, while the maximum mass of a differentially rotating,

hypermassive star is typically 50% larger than the maximum mass of a nonrotating star constructed from the same

realistic nuclear EOS, the increase is less than that for a polytrope.

16.3 Fully relativistic simulations 557

Merger

Black hole

0.7− 0.8

< 0.7− 0.8

Black hole

+ small disk

no SGRBno SGRB

SGRBSGRB

+ massive

disk

B-field

J-transport

Spheroi

HMNS

Ellipsoid

Black hole

+ heavy disk

M < M

thr

M > M

thr

M M

thr

Figure 16.12 Plausible routes for the formation of a short-hard gamma-ray burst (SGRB) central engine

following the merger of a binary neutron star. Here “HMNS” stands for hypermassive neutron star remnant and

represents the mass ratio of the initial stars. For HMNS remnants, “GW” vs. “B-ﬁeld J-transport” denotes the

outward transport of angular momentum dominated by gravitational wave emission vs. magnetic torques. [From

Shibata and Taniguchi (2006).]

(2006) also ﬁnd that in the case of prompt black hole formation the disk mass increases

sharply with decreasing q for a ﬁxed ADM mass and EOS, as shown in Figure 16.11.

By contrast, in the case of hypermassive remnant formation, followed by delayed collapse

to a black hole, the disk mass is likely to exceed 0.01M



, independently of the mass ratio.

If the dissipation of angular momentum responsible for inducing the collapse is due solely

to the emission of gravitational waves from the ellipsoidal remnant, the disk mass can only

be estimated, and amounts to 0.01–0.03M



If, however, the dissipation is accelerated

by the ampliﬁcation of a seed magnetic ﬁeld in the remnant, the evolution of the system

following collapse can be followed using black hole excision until a quasistationary state

is reached. At this point the disk mass is found to be roughly 0.1M



(see Figure 16.11).

Several scenarios now suggest themselves by which the merger of a binary neutron star

can trigger a short-hard GRB. Some plausible routes are summarized in Figure 16.12.

Another scenario for forming the central engine of a short-hard GRB is the merger of a

black hole-neutron star binary, which we will discuss in Chapter 17. While all of these

Shibata and Taniguchi (2006) therefore suggest that a merger with a smaller q may be a better candidate for producing

a short-hard gamma-ray burst central engine.

The duration of this nonaxisymmetric secular dissipation process, which typically lasts 50 ms, is too long to be tracked

reliably using a fully relativistic 3 +1 hydrodynamic code like the one of Shibata and Taniguchi (2006). However, it

has been possible to follow this dissipation epoch for incompressible (Miller 1974; Detweiler and Lindblom 1977)and

compressible (Ipser and Managan 1984; Lai and Shapiro 1995a) triaxial ellipsoids in Newtonian gravitation. These

treatments allow for differential rotation (vorticity) and viscosity and incorporate a gravitational radiation-reaction

potential. It is found that in the absence of viscosity, radiation-reaction forces typically drive a Jacobi-like ellipsoid

to a nonradiating triaxial state (a Dedekind ellipsoid), for which  = 0 in the inertial frame (a “stationary football”).

Other possibilites exist, however, depending on the vorticity and (conserved) circulation of the conﬁguration. For every

scenario, the emitted quasiperiodic waves exhibit a unique signature that may be detectable by a gravitational wave

laser interferometer; see Lai and Shapiro (1995a) and references therein.

558 Chapter 16 Binary neutron star evolution

Z/R

X/R

0.5

−0.5

−1

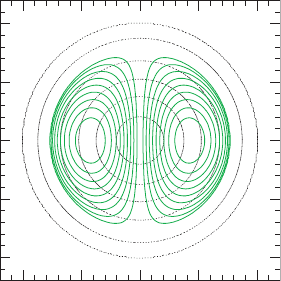
Figure 16.13 Magnetic ﬁeld lines in a widely separated, spherical neutron star companion as viewed in the

meridional plane. The star is an n = 1 polytrope with a rest mass

= 0.146 (the maximum being 0.180 for this

EOS). Dotted (black) concentric circles are rest-mass density contours drawn for

/ρ

max

= 0.9, 0.7, 0.5, 0.3, 0.1, and 0.001. Solid (green) lines show representative magnetic ﬁeld lines; the ﬁeld

is purely poloidal. Coordinates are in units of the stellar radius R.[FromLiu et al. (2008).]

scenarios still await detailed analyses, it seems clear that numerical relativity is capable of

supplying the computational ﬁrepower necessary to construct viable theoretical models.

Perhaps one of the most important roles of numerical relativity will prove to be laying the

theoretical groundwork for the simultaneous detection and identiﬁcation of a gravitational

wave signal and gamma-ray burst from the same cosmic source.

Magnetized binary neutron star mergers

Since neutron stars are threaded by magnetic ﬁelds, it is important to assess the effect of

such ﬁelds on binary mergers. The exterior ﬁelds of the two neutron stars will interact

during the inspiral phase, and in principle this could affect the dynamics and gravitational

waveforms. However, calculations show

that an exterior dipole ﬁeld has a negligible

inﬂuence provided the surface ﬁeld strength is below 10

G. Typical neutron stars are

expected to have ﬁelds much smaller than this, and only for extreme “magnetars” do

the inferred strengths begin to approach this limit. Any appreciable dynamical effect from

magnetic ﬁelds must thus originate from interior magnetic ﬁelds and can occur only during

and/or after the merger phase.

The effects of an interior ﬁeld on binary neutron star merger have been investi-

gated by Liu et al. (2008), who adopted the same basic HRSC GRMHD scheme of

Also, simulations coupled with broadband gravitational wave observations at frequencies between 500 and 1000 Hz

may constrain the neutron star EOS and measure its radius to an accuracy of δ R ∼ 1 km at 100 Mpc; Read et al.

(2009).

Ioka and Taniguchi (2000).

16.3 Fully relativistic simulations 559

t = 0.0 M

0.5c

Y/ M

−3

−6

−9

t = 49.7 M

0.5c

−3

−6

−9

t = 101.4 M

0.5c

−3

−6

−9

t = 151.0 M

0.5c

−3

−6

−9

t = 300.0 M

0.5c

X / M

−3

−6

−9

t = 347.6 M

0.5c

−3

−6

−9

t = 391.0 M

0.5c

−3

−6

−9

t = 188.3 M

0.5c

−3

−6

−9

t = 235.9 M

0.5c

−3

−6

−Z

−9

Figure 16.14 Snapshots of the rest-mass density and velocity ﬁeld in the equatorial plane during the merger of a

magnetized, neutron star binary. The initial binary is irrotational with n = 1 polytropic companions of

unequal-mass (the ratio of rest masses is q = 0.855). The binary has a total ADM mass

M = 0.290, a rest mass

= 0.317 and an angular momentum J/M

= 0.933. Density contours are drawn for

/ρ

max

(0) = 0.9, 0.8,...,0.1, 0.01, 0.001, and 0.0001. The initial magnetic ﬁeld proﬁle in each star is depicted

in Figure 16.13. The 3-velocity vectors are normalized as indicated above each frame. The black circle locates

the apparent horizon. [From Liu et al. (2008).]

Duez et al. (2005b) described earlier in the book and used to evolve rotating, magnetized

stars in Chapter 14.2.5. Liu et al. (2008) evolve binaries constructed via the conformal

thin-sandwich approach for n = 1 irrotational polytropes. Adopting equatorial symmetry,

they employ spatial grids with as many as 400 × 400 × 200 zones in x–y–z directions

560 Chapter 16 Binary neutron star evolution

0.004

−0.004

0.008

0.004

0.02

−0.02

−0.004

−0.008

200

100

300

500200

200

400

(t − r) / M

600

(a)

(b)

(c)

800

Re (rM

)

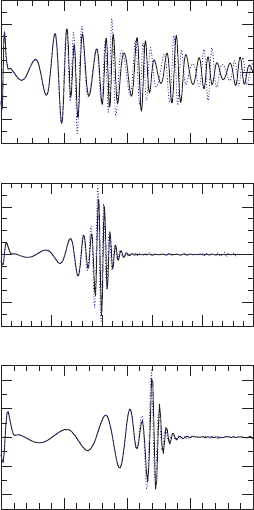
Figure 16.15 A comparison of gravitational waveforms for neutron star mergers in three different binary

systems; each system is treated with and without magnetic ﬁelds. Binary system (a) has low, equal-mass

companions and a total ADM mass

M = 0.269 and rest mass

= 0.292; it produces a hypermassive remnant.

Binary system (b) has high, equal-mass companions and a total ADM mass

M = 0.292 and rest mass

= 0.320; it leads to prompt collapse to a black hole. Binary system (c) has high, unequal-mass companions

and a total ADM mass

M = 0.290 and rest mass

= 0.317; it also leads to prompt collapse to a black hole.

The merger of system (c) is highlighted in Figure 16.14. The solid (dotted) lines show the waveforms for

unmagnetized (magnetized) binaries. [After Liu et al. (2008).]

(with the binary rotation axis along z) and use a simple FMR scheme

to enhance the

resolution and dynamic range. As a check, they ﬁrst repeated the simulations of Shibata

et al. (2003b) for several unmagnetized cases, using the same initial data as in Shibata et al.

(2003b), and found good agreement. For cases in which the mergers result in a prompt

collapse to a black hole, Liu et al. (2008) employ moving puncture gauge conditions

(Chapter 4.3) to extend the simulations in time to better determine the ﬁnal mass of any

debris that remains in an ambient disk about the remnant hole. They ﬁnd that the disk mass

is less than 2% of the total rest mass in all the cases studied. Liu et al. (2008) then add a

poloidal magnetic ﬁeld with a volume-averaged strength of about 10

G to the initial

conﬁgurations and explore the subsequent evolution; Figure 16.13 shows the initial

“Multiple-transition ﬁsheye” coordinates; see Chapter 14.2.3