Bayer R.G. Mechanical Wear Fundamentals and Testing, Revised and Expanded

Подождите немного. Документ загружается.

could then be represented as the sum of individual wear processes, for example,

total

¼ W

þ W

ð4:1Þ

where W

total

is the total wear, W

s-c-d

is the wear due to single-cycle deformation, and W

r-c-d

is the wear due to repeated-cycle deformation. Utilizing the expressions developed for

single-cycle deformation and fatigue wear, Eqs. 3.25 and 3.44, and assuming that a is

the fraction of the real area of contact that is wearing by single-cycle deformation, the

following equation can be proposed for this system:

total

¼ 2k

tan y

S þ OMGG

ð1  aÞ P

1þt=3

S ð4:2Þ

Figure 4.10 Examples of mild and severe wear scar morphologies for sliding. ‘‘Left side’’ shows an

example of mild wear scars obtained in a pin-on-disk test; ‘‘Right side’’ shows severe wear scars.

(From Ref. 80, reprinted with permission from ASME.)

Note that in this equa tion, P is the normal load and S is the distance of sliding. The other

symbols are as previously deﬁned for Eqs. (3.25) and (3.44). Sinc e each of the individual

mechanisms do not depend on the same parameters in the same manner, the dependency

of W

total

on these parameters would depend on the relative contribution of the individual

mechanisms to the total wear. For example, if a is very small, that is to say single-cycle

deformation is minor, the load dependency would be nonlinear and the wear behavior

would not be sensitive to the sharpness and size of the asperities. If a was near unity

(i.e., fatigue is minor), the wear would be sensitive to the asperities’ sharpness and the load

dependency would approach a linear one. For intermediate values of a, there would be

both a nonlinear dependency on load and a dependency on asperity size and shape, which

Figure 4.11 Transitions from mild to severe wear in the case of sliding wear of plastics. ‘‘A’’, poly-

imide=steel couple in a thrush washer test; ‘‘B’’, TFE composite=steel couple in a journal bearing

test. (‘‘A’’ from Ref. 23; ‘‘B’’ from Ref. 81.)

would be different from the ones associated with e ither mechanism. This trend is illus-

trated in Fig. 4.13, where it is assumed that a can be related to the load range. For light

loads, it was assumed that fatigue is negligible but at high loads, it predominates. Conse-

quently, the possibility of the simultaneous occurrence of several mechanisms can lead to a

wider range of behavior than those based on the individual mechanisms.

Figure 4.12 Sliding wear scars on ceramics, showing evidence of single-cycle deformation and

repeated-cycle deformation wear. (From Ref. 82; reprinted with permission from ASME.)

Figure 4.13 Example of combined wear behavior when there are two mechanisms present.

The individual mechanisms can also interact in a sequential fashion, giving rise to

another possible factor for complex wear behavior. For example, fatigue wear can weaken

the surface by the formation of cracks and allowing an adhesive event to remove the wear

particle. Mathematically, the wear may be described by the equation for adhesive wear,

where the wear coefﬁcient K is now dependent on the fatigue parameters of the system

in addition to the normal parameters associated with adhesion. In Eq. 3.7 for adhesive

wear, K is the probability that a given junction will result in wear. Assuming that this

probability is proportional to the fatigue wear rate (see Eq. (3.4 4)), the following equation

may be proposed for such a system:

W ¼

OMGG

2þt=3

S ð4:3Þ

where K

is the constant of proportionality. Comparison of this equation with Eq. 3.7 illus-

trates the complexity that the concept of one wear mechanism initiating another intro-

duces. Additional dependencies are introduced (e.g., the fatigue parameter t), and other

dependencies change (e.g., the dependency on load is no longer linear). Another example

of this type of sequential interaction would be either fatigue or adhesive wear mechanisms

forming debris, which then acts as an abrasive.

In considering these ways in which the basic wear mechanisms may interact in a

given situation, two points should be noted. In the case of parallel interaction, modiﬁca-

tion of the parameters effecting one of the wear modes may have little or no effect on the

overall wear behavior. However, in the sequential interaction, it should always have an

effect on the overall behavior. With the ﬁrst example, changing parameters to reduce fati-

gue wear would have negligible effe ct on the wear in the low load range, where abrasion

predominates. In the seco nd example, the overall wear would be reduced since it would

tend to reduce the effective probability of an adhesive failure. The second point to note

is that it is also possible to have both types of interactions (i.e., parallel and sequential)

occur in a given wear system. This confounded type of interaction can also contribute

to the complex nature of wear behavior.

While such interactions may make it necessary to consider more than one type of

mechanism as signiﬁcant, it is frequently not necessary to do so. It is generally possible

to consider one mechanism or type of mechanism as being the dominant and controlling

mechanism within limited ranges of tribosystem parameters, as illustrated by the wear

maps discussed in Sec. 3.9. In addition to different wear mechanisms being dominant

mechanisms in different ranges of operating parameters, wear mech anisms also differ in

their severity. This is illustrated in Fig. 4.14, where nominal ranges of a normalized and

dimensionless wear rate, O, for different mechanisms for sliding are plotted.



The dimen-

sionless wear rates are based on wear rates from wear situations in which the mechanism is

considered to be the dominan t type. There are several equivalent ways of deﬁning this rate,

which is shown by the following equations:

O ¼



ð4:4Þ



This wear coefﬁcient, O, is equivalent to the wear coefﬁcient, K, of a linear wear relationship, W ¼

KPS=p, where P is load, S is sliding distance, p is hardness, and W is wear volume.

O ¼



ð4:5Þ

In these equations, W is wear volume; h, wear depth; p, hardness; P, load; v, velocity;

s, contact pressure. The dot indicates wear rate with respect to time and the apostrophe

indicates wear rate with respect to sliding distance. In this ﬁgure, the limiting value

for O, which can be tolerated in engineering, is also indica ted. Applications requiring

long life and low wear values often require values of O one to two orders of magnitude

lower than this. It can be seen from this ﬁgure that adhesive, severe single-cycle defor-

mation, severe repeated-cycle deformation, and thermal mechanisms tend to be undesi-

rable forms of wear. Wear rates associated with these mechanisms tend to be higher

than those of the other types and generally unacceptable for two reasons. One is their

intrinsic severity, as indicated by the ranges of O. The other is that these forms of wear

tend to occur at higher velocities, pressures and loads than the milder forms of wear,

essentially compounding their undesirability in applications.

There is an overall trend in wear behavior with contact stress. In general, the severity

of wear increases with increasing stress. Not only does the severity of individual wear

mechanism tend to increase with increasing stress, increasing stress tends to lead to the

occurrence of more severe wear mechanisms. Both trends are indica ted in the wear maps

shown in Figs. 3.81–3.83 and in 4.15

. Empirical models for sliding, roll ing, and impact

wear also illustrate such a trend, as well as the general nature of the wear mechanisms.

For many wear situations, it is possible to correlate wear severity with the ratio of a

Figure 4.14 Nominal empirical ranges for normalized wear rates [(wear volume  hardness)=

(distance  load)] for different types of generic wear mechanisms.

contact stress to a strength parameter, such as contact pressure to hardness (30); see

Secs. 3 and Chapter 2 in Engineering Design for Wear: Second Edition, Revised and

Expanded (EDW 2E).

Important corollaries to these two trends are that materials and other design para-

meters should be selected to avoid severe wear mechanisms from occurring and that stress

levels should be reduced as much as possible to minimize wear.

4.3. TRIBOSURFAC ES

Since wear is primarily a surface phenomenon, surface properties are major factors in

determining wear behavior. Changes to surfaces are a frequent factor in transitions in wear

and friction behavior. Before discussing these, it is important to consider the general

nature of a tribosurface. A tribosurface consists of the basic or nominal material of the

surface plus any layers and ﬁlms that are present. This is illustrated by the schematic

cross-section for a typical metal surface shown in Fig. 4.16. There are numerous surface

properties that are associated with wear and friction that can affect overall behavior

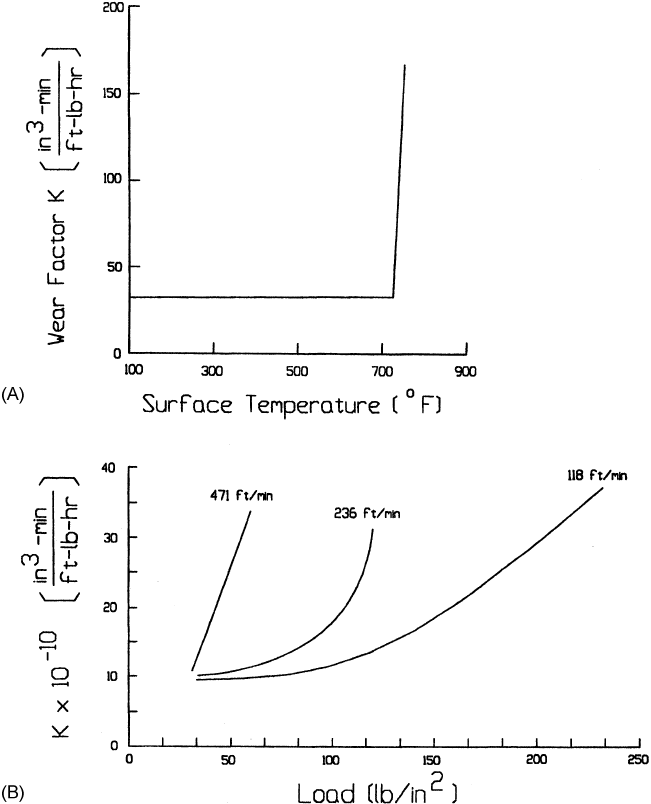
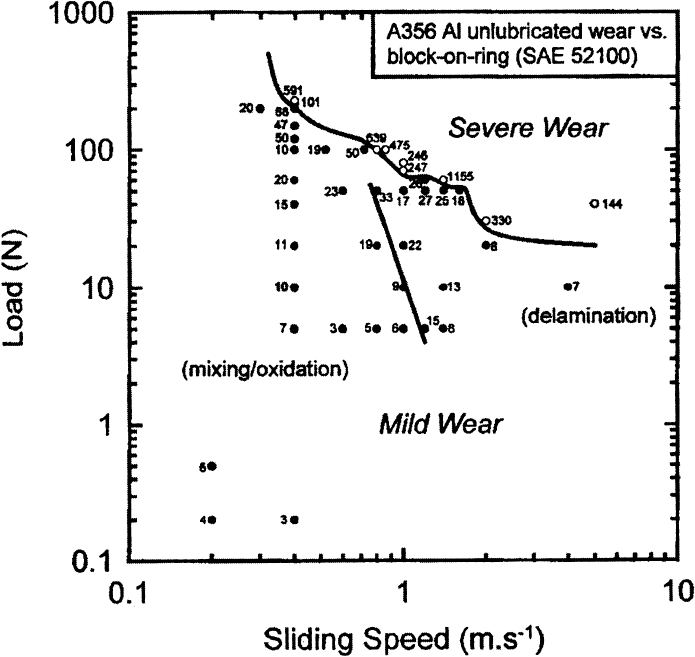
Figure 4.15 Empirical wear rate map for dry sliding wear of an aluminum block against a hard

steel ring. Contact stress increases with load. (From Ref. 80, reprinted with permission from Elsevier

Sequoia S.A.)

and cause transitions. The models for the primary wear mechanisms indicate that

geometrical, mechan ical, physical, and chemical parameters are involved. Geometrical

parameters include the overall shape of the contacting surfaces, as well as the distribution

and shapes of asperities. Mechanical parameters would include elastic moduli, hardness,

and fatigue parameters. Physical parameters could be work hardening characteristics,

diffusion constants, and lattice parameters. Composition and polarity of the surface are

examples of chemical factors. Thicknesses and other pro perties of the various layers

and ﬁlms are additional factors.

While surface parameters inﬂuence wear, surface parameters can be inﬂuenced by

wear. In effect, this means that wear and surface parameters are mutually dependent

and a stable wear situation would be one in which the surface pro perties do not change

with wear . If the wear process and the set of surface parameters are not mutually consis-

tent, the wear behavior will be unstable until a mutually consistent condition can be estab-

lished. This interdependency means that in addition to identifying the relationships

between wear and the initial parameters of tribosurfaces, as was done in the treatment

of the primary mechanisms, it is necessary to consider how the tribosurface may be modi-

ﬁed as a result of wear. The principle types of mo diﬁcations are treated in this section. The

manner in which these modiﬁcations can result in transitions in wear behavior is discussed

in the subsequent section.

Wear can cause geometrical changes both on a macro- and micro-scale. On a macro-

scale, the nature of the contact between two bodies changes, effecting the distributions of

stress and load across the contact region. An example of this would be a contact situation,

which initially is a point contact (e.g., a sphere against a plane). As wear occurs, one of the

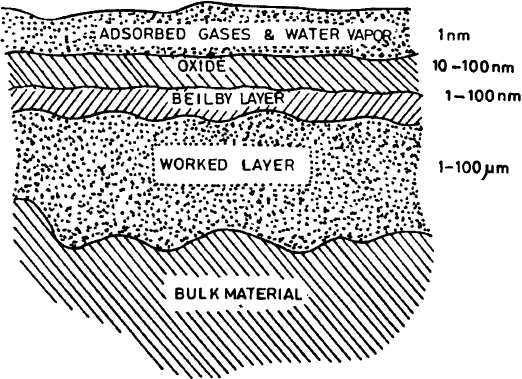
Figure 4.16 Illustration of an unlubricated metal surface. The worked layer is a region of the bulk

material that is worked-hardened as result of maching. The Beilby Layer is an amorphous or micro-

crytalline layer, resulting from melting and surface ﬂow of molecular layers during machining and

hardened by subsequent quenching. While all these layers are typical of most engineering surfaces,

an oxide layer, Beilby Layer, and worked layer may not be present with all metals and maching pro-

cesses. In general, the thickness and properties of these layers depend on the material, environmental

exposure, and maching processes. (From Ref. 84, reprinted with permission from The McGraw-Hill

Companies.)

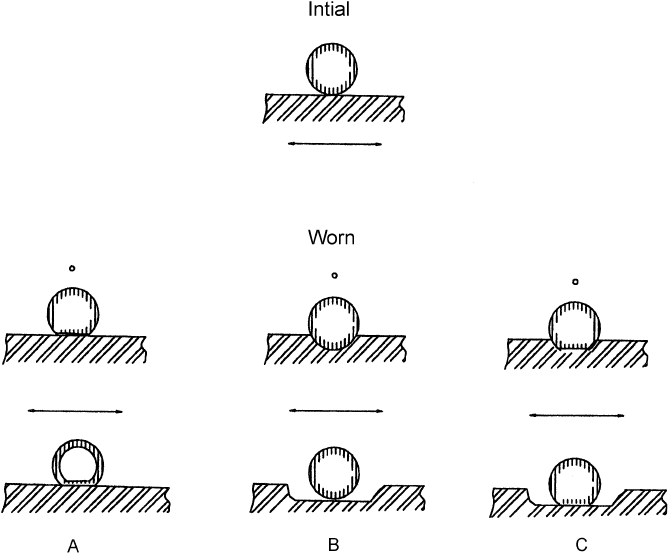
three contact situations indicated in Fig. 4.17 evolves. In two of these cases, the ﬁnal con-

tact situation is a conforming contact. In the third, ‘‘b’’, it changes from a point contact to

a line contact. This type of change is further illustrated in Fig. 4.18, which shows proﬁlo-

meter traces of a ﬂat surface and a sphere after some wear was produced on the ﬂat sur-

face. Another example of a macro-geometrical change is that which takes place between

two ﬂat surfaces, which are initially misaligned. Initially, the contact is conﬁned to the

region near the edges; with wear, however, contact over the entire surface can be estab-

lished. Such changes are extremely signiﬁcant in situations in which the wear depends

on stress, such as in mild sliding and impact wear situations (3,31). Such a change is related

to run-in behavior.

One way for micro-geometrical changes to occur is the result of asperity deforma-

tion as a result of contact. An example of this is shown in Fig. 4.19, where a proﬁl-

ometer trace through a wear track on a ﬂat surface is shown. A micrograph of the

surface is also shown. In this case, the tips of the asperities in the worn region appear

to be more rounded; asperity heights appear to be more uniform in the wear track as

well. In general, initial wear in sliding and rolling systems tends to increase the radius

of curvature of the asperities and to provide a more uniform distribution of asperity

heights. These changes tend to increase the number of asperities involved in the contact

as well as to reduce the stress associated with each junction. Initially, the asperity defor-

mation tends to be in the plastic range, while subsequent engagem ents would likely

Figure 4.17 Changes in the contact conﬁguration as a result of wear for a sphere sliding against a

plane. ‘‘A’’, only the sphere wears; ‘‘B’’, only the ﬂat wears; and ‘‘C’’, both the sphere and the ﬂat

wears.

result in elastic deformation as a result of these changes. As material is worn from the

surface, the general result is a different micro-geometry or topography, characteristic of

the wear processes involved. An example of this would be the striations that result from

abrasive wear; another might be adhesive wear fragments attached to the surface or the

roughening on the surface caused by erosion. Micrographs illustrating the morphologi-

cal features of worn surfaces are shown in Fig. 4.20 for a variety of conditions. Signiﬁ-

cant changes in surface topography are evident in these micrographs.

In addition to these geometrical changes associated with wear, other changes which

inﬂuence the physical and mechanical properties of tribosurfa ces can occur, as can changes

in material composition and structure. An example of these types of changes is the

Figure 4.18 (‘‘A’’) Proﬁlometer traces of sphere and a wear scar, produced by the sphere, are

superimposed, illustrating the conforming nature of the worn contact. (‘‘B’’) Micrographs of the

sphere and ﬂat after wear are also shown. (Unlubricated sliding between a 52100 steel sphere and

a 1050 steel ﬂat.) (From Ref. 52, reprinted with permission from Elsevier Sequoia S.A.)

Figure 4.19 An example of asperity modiﬁcations in the early stages of wear. The micrograph and

the proﬁlometer trace are for a Monel C Platen, worn by a 52100 steel sphere in lubricated sliding.

The wear track is located between the vertical lines on the trace. (From Ref. 52, reprinted with per-

mission from Elsevier Sequoia S.A.)

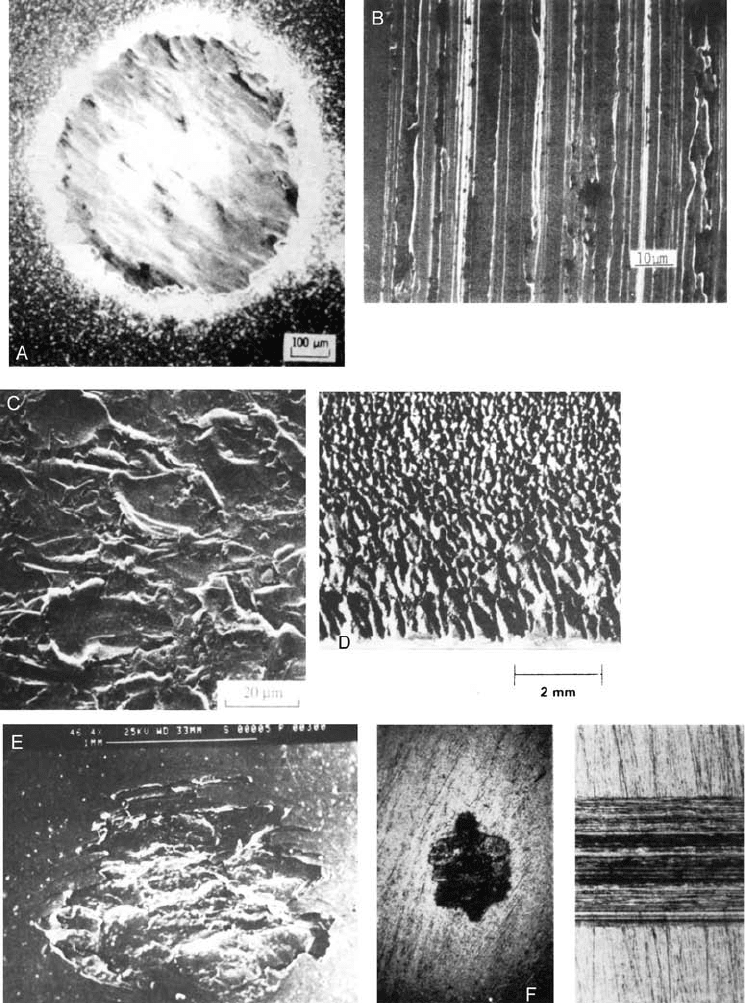
Figure 4.20 Examples of changes in surface topography as a result of wear under different condi-

tions. ‘‘A’’, fretting; ‘‘B’’, sliding; ‘‘C’’, erosion; ‘‘D’’, erosion; ‘‘E’’, rolling; ‘‘F’’, sliding; ‘‘G’’ and

‘‘H’’, compound impact; ‘‘I’’, erosion; ‘‘J’’, slurry erosion. (‘‘A’’ from Ref. 85; ‘‘B’’ from Ref. 83;

‘‘C’’ from Ref. 87; ‘‘D’’ from Ref. 88; ‘‘E’’ from Ref. 89; ‘‘F’’ from Ref. 52; ‘‘G’’ and ‘‘H’’ from

Ref. 3; ‘‘I’’ from Ref. 90; and ‘‘J’’ from Ref. 91. ‘‘A’’, ‘‘B’’, ‘‘E’’, ‘‘I’’, and ‘‘J’’ reprinted with permis-

sion from ASME; ‘‘G’’ and ‘‘H’’ reprinted with permission from Elsevier Sequoia S.A.; and ‘‘C’’ and

‘‘D’’ reprinted with permission from ASM International.)