Bayer R.G. Mechanical Wear Fundamentals and Testing, Revised and Expanded

Подождите немного. Документ загружается.

Because of this difference, it is necessary to modify the equation for single-cycle wear for

applicability to erosion situations. A simple way of extending this equation to particle ero-

sion is as follo ws (70).

The equation for single-cycle wear, Eq. (3.20), relates wear to the normal load. The

ﬁrst step in the derivation is to convert from normal load to frictional load, F. This is done

by means of Amontons’ Law, Eq. (1.1), namely,

F ¼ mP ð3:98Þ

Equation (3.20) then becomes

V ¼

KðFxÞ

ð3:99Þ

where the product Fx represents the energy dissipated by sliding during the impact.

The total kinetic energy of a particle stream of total mass, M, and particle velocity, n ,is

given by

E ¼

ð3:100Þ

As a result of the impact with the surface, a fraction, b, of the energy is dissipated in the

form of wear. Equating this loss to Fx, the following expression is obtained:

V ¼

KbMv

2mp

ð3:101Þ

In erosion, it has been established that the angle at which the stream impi nges the

surface inﬂuences the rate at which material is removed from the surface and that this

dependency is also inﬂuenced by the nature of the wearing material (70,159). This is shown

in Fig. 3.80. Such a dependency is to be anticipated. This can be seen by considering the

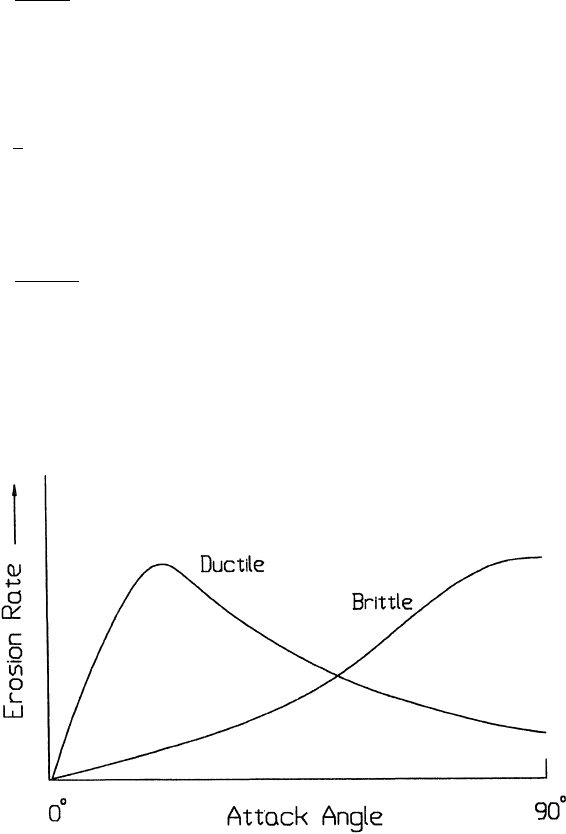
Figure 3.80 The effect of attack angle on erosion rates of ductile and brittle materials. (From Ref.

194.)

impact of a single particle with a surface. The angle determines the relative magnitude of

the two velocity components of the impact, namely the component normal to the surface

and the one parallel to the surface. The normal component will determine how long the

impact will last, that is, the contact time, t

, and the load. The product of t

and the tan-

gential velocity component determine the amount of sliding that takes place. The tangen-

tial velocity component also provides a shear loading to the surface, which is in addition to

the normal load related to the normal component of the velocity. Therefore, as the angle

changes, the amount of sliding that takes place also changes, as does the nature and mag-

nitude of the stress system. Both of these aspects inﬂuence the way a material wears. These

changes would also imply that different types of materials would exhibit different angular

dependencies as well.

As can be seen in Fig. 3.80, the effect of angle on erosion rate is signiﬁcantly different

for ductile and brittle materials. W ith brittle material, the maximum erosion rate occurs at

normal impact, while for ductile material s it occurs at some intermediate and generally

much smaller angle. These differences can be understood in terms of the predominant

modes of damage associated with these types of materials.

As discussed in Sec. 3.3, brittle fracture tends to increase the amount of wear over

that caused by displacement, that is by cutting and plowing. As indicated in Fig. 3.20, this

could be by as much as 10 . As a general rule, brittle materials are more likely to fracture

under normal impact conditions, that is, impacting velocity perpendicular to the surface,

than ductile materials. Consequently, as the erosive condition moves from a more grazing

situation to a more normal impact, brittle materials would experience a greater tendency

to experience brittle fracture, which would tend to increasingly mask the ductile or cutting

contributions. For brittle materials, the erosion rate would then be expected to mono-

tonically increase with the angle.

For ductile materials, cutting and plowing are the predominant modes and fracture

is negligible. The model for single-cycle deformation indicates that the wear due to cutting

and plowing is proportional to the product of load and distance (see Eq. (3.20)). Since load

increases with angle and sliding decreases with angle, an intermediate angle should exist

where the product of the two is maximum.

This angular dependency is contained in b in Eq. (3.101). Assuming that b can be

separated into an angular factor, F, and a factor independ ent of angle, b

, and combining

several of the material-sensitive parameters and num erical factors into one, K

, the follow-

ing expression can be obtained:

V ¼

FMv

ð3:102Þ

Examining this equation for erosive-wear volume, it can be seen that it does not provide

an explicit dependency on duration or exposure. However, such a dependency is implicitly

contained in M, the total mass of particles. If Q is particle mass per unit time, then M is

Qt, where t is the time of exposure to the particle stream. Including this into Eq. (3.102),

the following form is obta ined for particle erosion:

V ¼

ð3:103Þ

Another variation of Eq. (3.102) is frequently encountered in the literature. Compar-

ison of erosive wear situations and resistance to erosion is often done in terms of the rela-

tive amount of material removed from the surface to the amount of abrasive particle

causing the wear (160). With d as the density of the particles, the following equation can be

obtained:

dFv

ð3:104Þ

where V

is the volume of abrasive used to produce the wear.

A compilation of values for the erosive wear coefﬁcient, K

, is given in Table 3.9.

Comparing these values to the values for wear coefﬁcients for abrasion, Table 3.8, it

can been seen that they are very similar. This is consistent with the underlying hypothesis

that the same wear mechanisms occur in both situations.

Equations for solid particle erosion, which are equivalent to Eqs. (3.94) and (3.96)

for abrasion, can be developed in a similar manner. These are:

V ¼ K

Qt ð3:105Þ

V ¼

ð3:106Þ

Equation (3.106) applies when the surface is harder than the particles. In general, the ero-

sive wear coefﬁcients in these equations for particle erosion have similar sensitivities to

their counterparts for abrasion , that is, they can be affected by characteristics of the abra-

sives, type of material or simply material, atmosphere, and ﬂuid media (161).

In controlling abrasive wear, the most signiﬁcant feature is that once the wearing

surface becomes harde r than the abrasive, wear rates are dramatically reduced. The effect

here is equivalent to the use of lubricants to control adhesive wear. Both give orders-of-

magnitude improvement. Further discussion and examples of abrasion and particle ero-

sion can be found in Chapter 9, and in Chapters 5 and 7 of Engineering Design for Wear:

Second Edition, Revised and Expanded.

3.9. WEAR MAPS

Wear maps are graphical techniques used to characterize various aspect of wear behavior in

terms of independent operational parameters of the tribosystem, such as speed and load.

Various forms of wear maps are typically used to identify ranges of these parameters with

wear mechanisms, wear rates, and acceptable operating conditions. Generally, they are two-

dimensional graphs where the axes are the independ ent operati onal parameters. Curves are

plotted on these grap hs to separate regions of different wear behavior and to represent

conditions of constant wear rate. In addition to the generic name of wear map such plots

are also referred to as wear mechanism maps, wastage maps, material performance maps,

wear transition maps, wear rate maps, and contour wear maps, depending on their nature

and use. Examples of different types of wear maps are shown in Figs. 3.81–3.84 and

3.86–3.90. Figures 3.81–3.84 are examples of ones used for sliding wear; Figs. 3.86

and 3.87, for tool wear; and Figs. 3.88, 3.89, and 3.90, for solid particle erosion. While

maps of these types can be developed on a purely theoretical or experimental basis, most

are primarily empirical-based. However, theoretical considerations are often involved to

facilitate the construction and to minimize the amount of data required (106,109,162–

170).

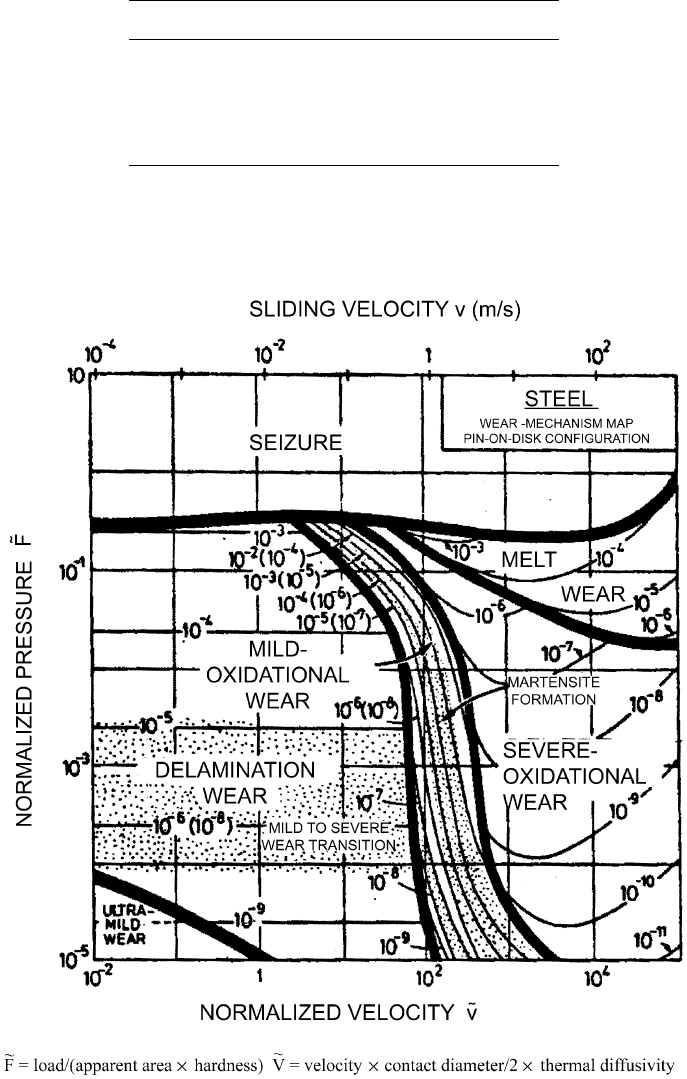
Table 3.9 K

Values for Erosion

Target material K

Soft steel 8  10

3

–4 10

2

Steel 1  10

2

–8 10

2

Hard steel 1  10

2

–1 10

1

Aluminum 5  10

3

– 1.5  10

2

Copper 3  10

3

– 1.3  10

2

Figure 3.81 Wear map developed for unlubricated sliding between self-meted steel. (From Ref.

109, reprinted with permission from Elsevier Science Publishers.)

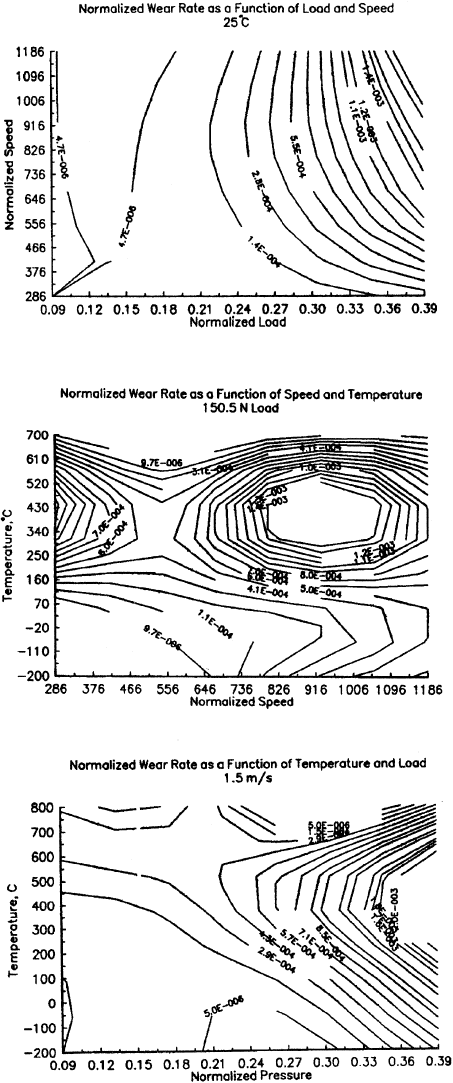
Figure 3.82 Wear mechanisms maps used to characterize the unlubricated sliding wear behavior of

self-mated 440C stainless steel. (From Ref. 163, reprinted with permission from Elsevier Sequoia

S.A.)

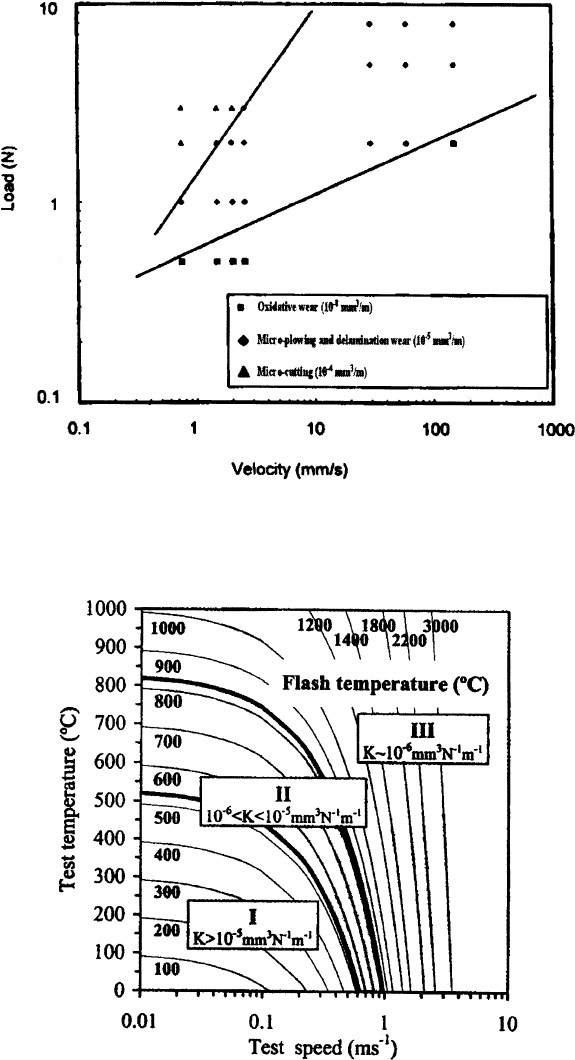
Figure 3.83 Wear map characterzing the wear behavior of Cr ion-implanted iron sliding against a

hard steel counterface and lubricated with liquid parafﬁn. (From Ref. 168, reprinted with permission

from Elsevier Sequoia S.A.)

Figure 3.84 Example of wear maps used to characterize the unlubricated wear behaviour of silicon

nitride ceramics sliding against steel. These maps are referred to as wear transition maps and show

the transition in wear behavior of the ceramic as function of ambient temperature and speed. (From

Ref. 136, reprinted with permission from Elsevier Sequoia S.A.)

Figure 3.85 Examples of wear scars on silicon nitride ceramics in the different regions identiﬁed in

wear transition maps, such as illustrated in Fig. 3.84. ‘‘A’’ is for 22



C and 0.5 m=s; ‘‘B’’ is for 200



and 0.5 m=s; ‘‘C’’ is for 22



C and 3.5 m=s. (From Ref. 136, reprinted with permission from Elsevier

Sequoia S.A.)

Figure 3.86 Wear map for ﬂank wear of Ti-N coated steel tool. Map is used to identify acceptable

regions of operation. (From Ref. 167, reprinted with permission from Elsevier Sequoia S.A.)

Figure 3.81 shows the ﬁrst wear map that was developed to illustrate the wear

map concept (109). This map is one proposed for unlubricated or dry sliding between

steels, using normalized pressure and normalized velocity as the axes. In it the bound-

aries between regions of different wear mechanisms are identiﬁed, as well as the locus

of pressures and velocity conditions for a constant normalized wear rate within those

regions.

Figure 3.87 Wear map for ﬂank wear of Ti-N coated steel tools, identifying regions of different

wear behavior. These regions are superimposed on those used to identify acceptable performance

(see Fig. 3.86). (From Ref. 167, reprinted with permission from Elsevier Sequoia S.A.)

Figure 3.88 Example of wear maps used to characterize erosion. This type of map is referred to as

velocity-particle size wastage maps. Axes are particle velocity and particle size. (From Ref. 164,

reprinted with permission from Elsevier Sequoia S.A.)

Another example of a wear map is the contour wear maps developed for 440C stain-

less steel for use in high-pressure oxygen turbopumps, shown in Fig. 3.82 (163). In these

maps contour lines of constant wear rate are plotted. For these applications, it was desir-

able to characterize wear behavior in terms of three operating parameters, load, speed, and

ambient temperature. To accomplish this, wear maps were developed for different combi-

nations of these parameters, as illustrated in the ﬁgure. In this case, the wear map can be

thought of as a three-dimensional wear space with axes of load, speed, and temperature,

where surfaces of constant wear rate can be identiﬁed. The two-dimensional graphs can

then be thought of as planes in that space and the contour lines are the intersection of

those planes with these surfa ces.

A less complex wear map than these two examples is shown in Fig. 3.83. In this

case load and speed are the operating variables of interest (168). This wear map is an

example of a wear mechanism map. In this map, three regions of diff erent wear

mechanisms, each with a characteristic order-of-magnitude wear rate, are identiﬁed.

These regions were identiﬁed by physical examination of the worn surfaces and wear

rate determination.

Wear transition maps are illustrated in Fig. 3.84. In this case, ambient temperature

and speed are the axes (165). In this map, three different regions of wear behavior are iden-

tiﬁed and correlated with different ranges of a wear coefﬁcient for a ceramic slider. In this

tribosystem, wear behavior can be correlated to ﬂash temperature and isothermal contours

for ﬂash temperature are also plotted on the map. For this tribosystem, the three different

Figure 3.89 An example of the types of wear maps used to characterize erosion. This type is

referred to as materials performance maps. In these, the different regions are used to identity wastage

conditions for individual materials. In this particular map, the various shaded regions are regions of

low wastage for the individual materials. The clear region is a region of medium wastage for all the

materials. (From Ref. 164, reprinted with permission from Elsevier Sequoia S.A.)

wear regions are a result of differences in the formation of triboﬁlms on the surface of the

ceramic, as shown in Fig. 3.85. In region I, there is no evidence of transfer and a triboﬁlm

is not formed. In regions II and III, higher ﬂash temperature promotes adhesion of tool

steel wear particles to the ceramic surface. In region II, there is partial ﬁlm formation.

In region III, the ﬁlm is more uniform and extensive.

Wear maps are also used to characterize tool wear and to determine optimum oper-

ating conditions for least tool wear (162,166,167,169). Example of a wear rate map used

for this purpose is shown in Fig. 3.86 (167). In this case, the axes are feed rate and cutting

speed. The boundaries of the regions are based on wear rate. Mechanism information can

also be placed on the map to provide a wear mechanism map. This is shown in Fig. 3.87,

where three regions of different dominant mechanism are identiﬁed. It is can be seen in this

map that the least wear region includes two different mechanism regions. With tools, such

maps are used to characterize both ﬂank wear, as illustrated in the ﬁgures, and crater wear

(169).

The use of wear maps in solid particle erosion is illustrated in Figs. 3.88, 3.89, and

3.90. Three different types of wear maps are used (164). One is referred to as wastage maps

and the axes are generally particle size and velocity. Figure 3.88 is an example of this. In

this case, the maps identify regions of high medium, and low wastage rates, which were

based on the depth of wear, x, in a standard test. High wastage rate was equivalent to

x  8 mm; medium, 4 mm  x < 8 mm; low, x  4 mm. These levels were based on the

approximate levels of wastage that can typically be tolerated in a ﬂuid bed conveyer.

Material performance maps are developed from this by overlaying the wastage maps

obtained for different materials. In this case, it was for diffe rent metal matrix compo-

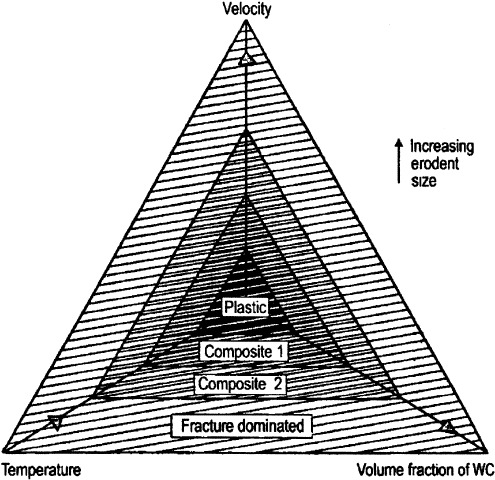
Figure 3.90 An example of four-variable wear map used to describe erosion behavior. This map is

used to characterize wear behavior in terms of wear mechanisms and use erodent size, erodent velo-

city, temperature, and material composition as parameters controlling the wear. (From Ref. 164,

reprinted with permission from Elsevier Sequoia S.A.)