Bayer R.G. Mechanical Wear Fundamentals and Testing, Revised and Expanded

Подождите немного. Документ загружается.

following equation (37):

F ¼



1=2

3=2

ð3:39Þ

Substituting in Eq. (3.38) and reducing, the following equation is obtained:

V ¼ OMGG

1:5

L ð3:40Þ

where

O ¼ 0:42  0:64

ð3:41Þ

M ¼

ðt1:5Þ=3

ð3:42Þ

G ¼

ðt1:5Þ=2

t=3

ðt1:5Þ=2

ð3:43Þ

This simple model provides a general identiﬁcation of the typical parameters, which inﬂu-

ence fatigue wear. Fatigue parameters of the mate rial are one type of parameter which

affect fatigue wear, as illustrated by t and S

in the wear equation. In addition several

of what might be termed mechanical parameters of the system are also involved. These

are the geometrical features of the surfaces (roughness and apparent area of contact), load,

elastic constants of the materials (Young’s modulus and Poisson’s ratio), and the co-

efﬁcient of friction of the material pair. The signiﬁcance of individual parameters is inﬂu-

enced by the overall fatigue behavior of the material, as illustrated by the effect of t, the

exponent of Wohler’s equation, on exponents associated with these parameters. This over-

riding inﬂuence of the fatigue behavior can be illustrated with the present model by noting

that in fatigue studies values of t as low as 2 and in excess of 20 have been found for dif-

ferent materials (78,90).

While the gen eral nature of this equation for fatigue wear does not change with the

nature of the asperity distribution, the exponents can change. For example, if a uniform

distribution is assumed, the following is obtained:

V ¼ OMGG

ð1þt=3Þ

L ð3:44Þ

O ¼ 0:36  0:58

ð3:45Þ

M ¼

ð2t=31Þ

ð3:46Þ

G ¼

ðt=30:5Þ

t=3

ð2t=31Þ

ð3:47Þ

As illustrated by these results, different fatigue relationships and assumptions regarding

asperity loading and distribut ions can affect the depe ndency on load. Other models for

fatigue wear and experimental data indicate that the load dependency can generally be

represented by a power relationship, P

. While some models for fatigue wear result in

values of n near 1 for speciﬁc conditions, signiﬁcantly larger values, for example, 3 or

larger are also possible (26,27,78,85,86,91,92). Equations (3.40) and (3.44) illustrate this.

This range of n values is consistent with empirical observations. For example, the wear

test data for bainitic steels, shown in Fig. 3.41, indicate a range of 2–6 for n. In studies

by the author values in the range of > 1to < 4 have been observed, as well (93).

On the other ha nd, a near-linear relationship was found in some studies of polymer

wear (94).

Theoretical models and empirical observations suggest that the general form for fati-

gue-like repeated-cycle deformation wear is

V ¼ KP

S; n  1 ð3:48Þ

where S is the distance of sliding. For rolling and impact, S can be replaced by number of

impacts or revolutions. As can be inferred by comparison with Eqs. (3.40) and (3.44),

K depends on a range of material and contact parameters, as well as the type of fatigue

process, but not directly on hardness. As a result, there are two signiﬁcant differences

between this equation and the ones for adhesive, Eq. (3.7), and single-cycle deformation

wear, Eq. (3.25). One is that the relationship for repeated-cycle deformation does not

contain an explicit dependency on hardness as the ones for adhesive and single-cycle

deformation wear. The other is that the dependency on load is different. For adhesion

and single-cycle deformation, there is a linear relationship, while for repeated-cycle defor-

mation, it is generally non-linear. Models and empirical information indicate that n is a

function of materials, wear process, and asperity distribution.

Figure 3.41 The effect of load on the unlubricated sliding wear of several bainitic steels. (From

Ref. 96.)

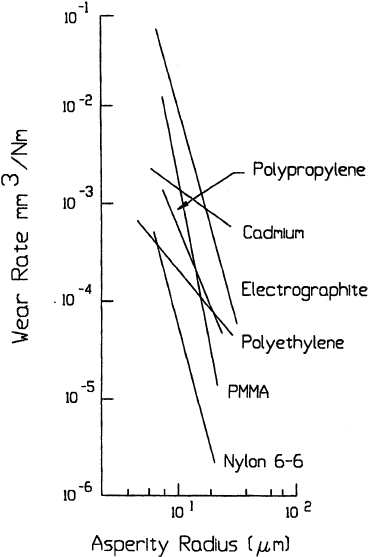
The dependency of fatigue wear on the radius of the asperity tip, b, was investigated

for a variety of materials (95). In general, a high-order de pendency on b was found. Some

of the data are shown in Fig. 3.42. These data suggest that wear rate is proportional to b

6

or b

5

for severa l of the system investigated. In terms of the Wohler-based models, this

implies a value of the order of 10 for t, which is similar to the exponents relating stress

and incubation cycles, as illustrated by Eq. (3.30).

More fundamental approaches to fatigue wear have also been proposed, such as

dislocation theory (26,27,96), and fracture mechanics (85, 86). These models, while indi-

cating some of the underlying features and concerns in fatigue wear, have not been as

useful in practice, as the models or concepts based on more simple engineering concepts

for fatigue or using Eq. (3.44) as an empirical relationship. However, such concepts can

provide some insight into the relative behavior of different materials with respect to this

type of wear.

Because of the incubation period of fatigue-like repeated-cycle deformation mechan-

isms, these mechanisms tend not to be signiﬁcant in the early stages of wear or early life of

a component. Adhesive and single-cycle deformation mechanisms tend to be more signiﬁ-

cant in these. Fatigue-like mechanisms become more signiﬁcant and often are the domi-

nant mechanisms in later stages of wear associated with long-term behavior. The

severity of the wear resulting from repeated-cycl e deformation mechanisms tend to be pro-

portional to (stress=strength parameter)

. The exponent is typically greater than 1 and can

be high, for example, in the range of 10. Ho wever, the strength parameter is generally

something other than hardness.

Figure 3.42 Effect of asperity radius on initial wear rate of several materials sliding against an

unlubricated mild steel surface. (From Ref. 22.)

3.5. OXIDATIVE WEAR PROCESSES

The basic concept for these processes is that wear occurs by the continuous removal of

oxide layers as a result of sliding contact between asperities. In between contacts, the oxide

regrows on these denuded areas of the surface and is again removed with subsequent

asperity engagem ent. Characteristic of such processes is the formation of a glassy-like

layer on the surface and subsequent appearance of fractures and denuded regions in the

layer (97,98). Examples of this are shown in Fig. 3.43. Under these conditions, the wear

rate is generally low and ﬁne wear particles of oxides are observed.

A simple model for metals can be used to describe the basic elements of oxidative

wear (99,100). The implicit assumption of the model is that the weakest point is at the

interface between the substrate and the oxide and that as the result of sliding engagement

the oxide layer ﬂakes off at the interface, much like a coating or plating with poor adhe-

sion. The overall sequence is shown in Fig. 3.44.

It is assumed that the real area of contact can be represented as a uniform array of

circular junctions as sho wn in Fig. 3.45. The wear rate associated with a junction, w

,is

given by

ð3:49Þ

pad

ð3:50Þ

where 2a is the diameter of the circular junction and d is the thickness of the oxide ﬁlm.

The wear rate of the surface would then be

w ¼

pnad

ð3:51Þ

where n is the number of junctions.

Assume that the growth of the oxide follows a logarithmic law, which is gen erally

true for the initial growth on clean metal surfaces (99). In this case, the thickness, d,is

given by the following equation:

d ¼ b ln

þ 1



ð3:52Þ

where t is time and b and t are parameters associated with the kinetics of the oxidation

process. b is a constant dependent on material and temperature and t is a constant depen-

dent on material. Assuming that each time a junction is formed, the oxide layer is

removed, t would be the average time it takes for a junction to reform. If S is the average

spacing between junctions,

t ¼

ð3:53Þ

where v is the sliding velocity. For many sliding situations, this relationship may be sim-

pliﬁed by noting that t=t is frequently less than 1. For example, for the case of iron, t is in

the range of seconds. For a sliding speed of 0.01 in.=s and asperity spacing of 0.002 in., t is

less than 1 s. Hence, for sliding Eq. (3.52) can be written as

d 

ð3:54Þ

Figure 3.43 Examples of sliding wear surfaces after the formation of an oxide layer. In ‘‘A’’, the

layer appears continuous and uniform. In ‘‘B’’ and ‘‘C’’, the layers are cracked and fractured. ‘‘A’’

and ‘‘C’’ are for self-mated unlubricated fretting between Incone1 specimens at elevated temperature,

540



C and 700



C, respectively. ‘‘B’’ shows the appearance of the wear scar on a steel pin after sliding

on an unlubricated molybdenum disk. (‘‘A’’ and ‘‘C’’, from Ref. 182; ‘‘B’’, from Ref. A107; reprinted

with permission from ASME.)

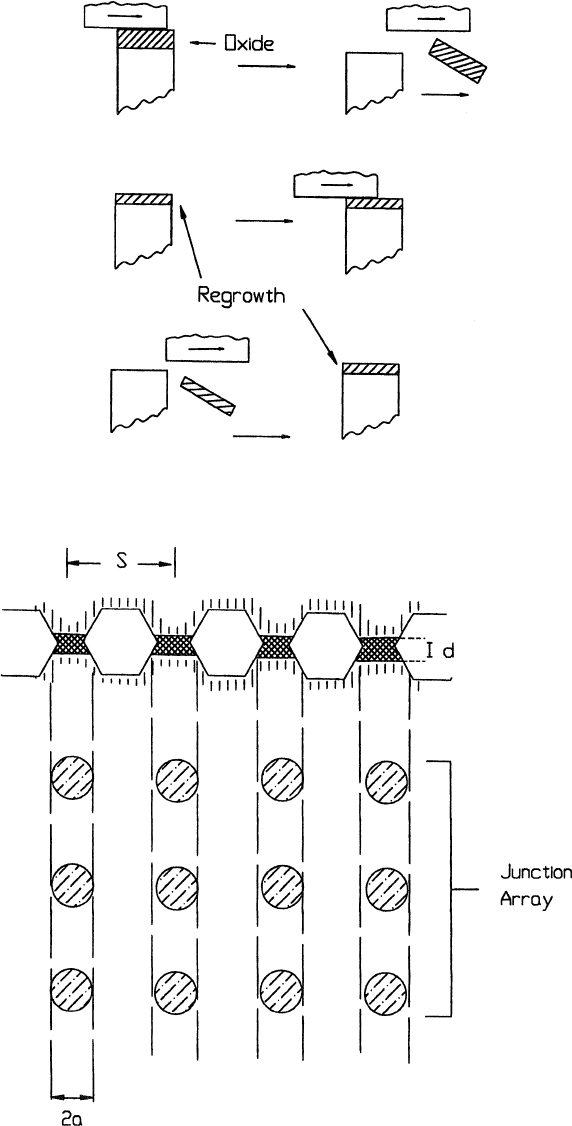
Figure 3.44 Model for oxidative wear.

Figure 3.45 Junction array used with model for oxidative wear.

d ¼

ð3:55Þ

The average spacing of junctions, S, is given by

S ¼



1=2

ð3:56Þ

where A

is the apparent area of contact. Assume that the oxide layer is too thin to sig-

niﬁcantly affect the mechanical properties of the surface and consequently the contact

situation. Assuming that the asperi ties are plastically deformed, the real area of contact

is equal to the load, P, divided by the penetration hardness of the softer material, p. Con-

sequently,

n ¼

ð3:57Þ

Utilizing these relationships, it can be shown that

w ¼

2tv



1=2

ð3:58Þ

W ¼

2tv



1=2

L ð3:59Þ

where W is the volume of wear and L is the distance of sliding.

The same equation would result if one did not assume that the oxide is always

removed at each junction formation. If K is the probability that the rupture of a junction

would result in the formation of a wear particle, the average time for oxide growth would

be K

1

(S=v) and the K’s would cancel in the ﬁnal expression. Simply, this means that fre-

quent removal of a thin oxide layer is equivalent to infrequent removal of thick oxide layer.

Other assumptions regarding the real area of contact can modify the dependencies

on mechanical parameters. For example, a reﬁned version of this model, which assumes

that the surface topography is describe d as a Gaussian distribution of conical asperities,

results in the following equation for W (101):

W ¼



1 

fðxÞ

fðxÞdx

ð3:60Þ

where

fðxÞ¼

ð2pÞ

1=2

x

ð3:61Þ

x ¼

ð3:62Þ

C is the separation of the center lines of the surfaces and s is the composite surface rough-

ness for the surfaces. x

is the value of x corresponding to the separation when there is

initial contact. As can be seen by comparison of the two equations for W, the dependencies

on the reaction parameters and speed remained the same but the dependencies on appar-

ent area of con tact, load, and hardness changed. Analysis of the term in the bracket shows

that while x depends on both load and roughness, its value is almost independent of load,

hardness, and roughness (101). This does not mean, however, that the wear is independent

of these parameters. As was stated previously, b is a function of temperature. This implies

that b is also a function of load, hardness, and sliding speed.

In general, b is related to temperature by means of an Arrhenius type of relationship,

namely,

b ¼ b

Q

=RT

ð3:63Þ

where b

is the Arrhenius constant for the reaction, Q

is the activation energy associated

with the oxide, R is the gas constant, and T is the temperature of the surface. On the basis

of a simple model for asperity temperature (102), T can be related to P, p and n by the

following:

T ¼ T



4Jðk

þ k

Þa

ð3:64Þ

where T

is the nominal temperature of the surface; m, the coefﬁcient of friction; P



, the

load on the junction; a, the radius of the junction; J, Joule’s constant; the k’s are the ther-

mal conductivities of the two bodies. P



and a are functions of P, p, and the asperity dis-

tribution as illustrated by Eq. (3.57). (See Sec. 3.6 for a discussion of frictional heating and

alternate equations for T.)

This simple model for oxidative wear indicates the various facto rs or parameters of a

tribosystem that can inﬂuence these types of mechanisms. These processes are dependent

on the chemical nature of the surface, reaction kinetics, mechanical and thermal properties

of the materials, micro- and macro-geometrical features of the two surfaces, and operating

conditions, that is, load, speed, and environment.

It has been shown that a simila r model can be used to describe some of the general

trends observed for cases of dry, sliding wear of steel surfaces (98,103,104). In this model,

it is assumed that there is a thin layer of oxide on the surface at all times. Since the growth

rate on clean surfaces and on oxidized surfaces tend to be different, this model uses a dif-

ferent relationship for oxide growth. Growth on oxide layers tends to follow a parabolic

relationship rather than a logarithmic one. As a result, this model uses the following equa-

tion rather than Eq. (3.52):

¼ bt ð3:65Þ

where m is the amount oxygen a unit area of surface has taken up in time t. m is related to

oxide thickness by the following equation:

m ¼ f r

d ð3:66Þ

is the density of the oxide and f is the fraction of the oxide that is oxygen. b again is

described in terms of an Arrhenius relationship.

This model allows the possibility of multiple engagements before a wear particle is

formed by assuming that a critical oxide thickness, d

, is required for fracture to occur.

This model resulted in the following equation for wear rate:

w ¼

3=2

Q

=RT

1=2

3=2

1=2

ð3:67Þ

In using this model to explain the behavior of wear rates observed in dry sliding experi-

ments with steels, it is necessary to make additional assumptions, primarily regarding n

and d

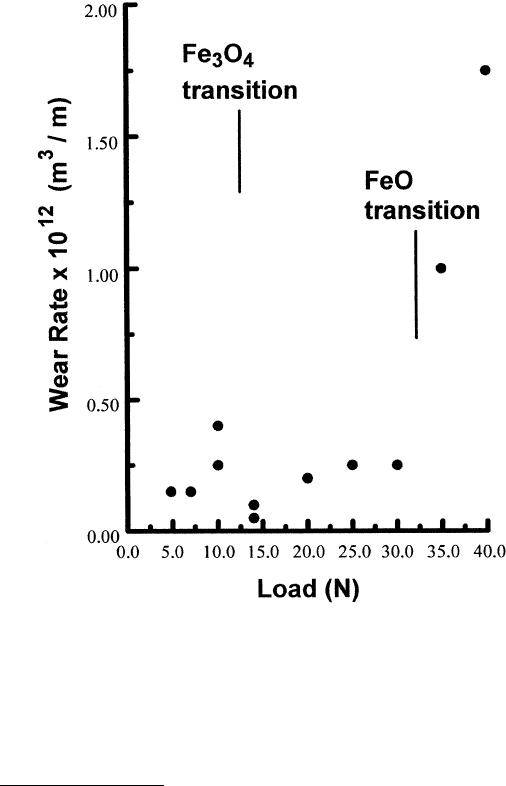
. Dry sliding data for EN8 steel are shown in Fig. 3.46. As can be seen in the ﬁgure,

transitions in wear rate were found to correlate with the occurrence of different oxides.

Oxidation studies have shown that there are three distinct regions of oxide growth with

different activation energies (105). These regions are described in Table 3.6. Regression

analysis of that data using this model indicated that it was necessary to assume that n

and d

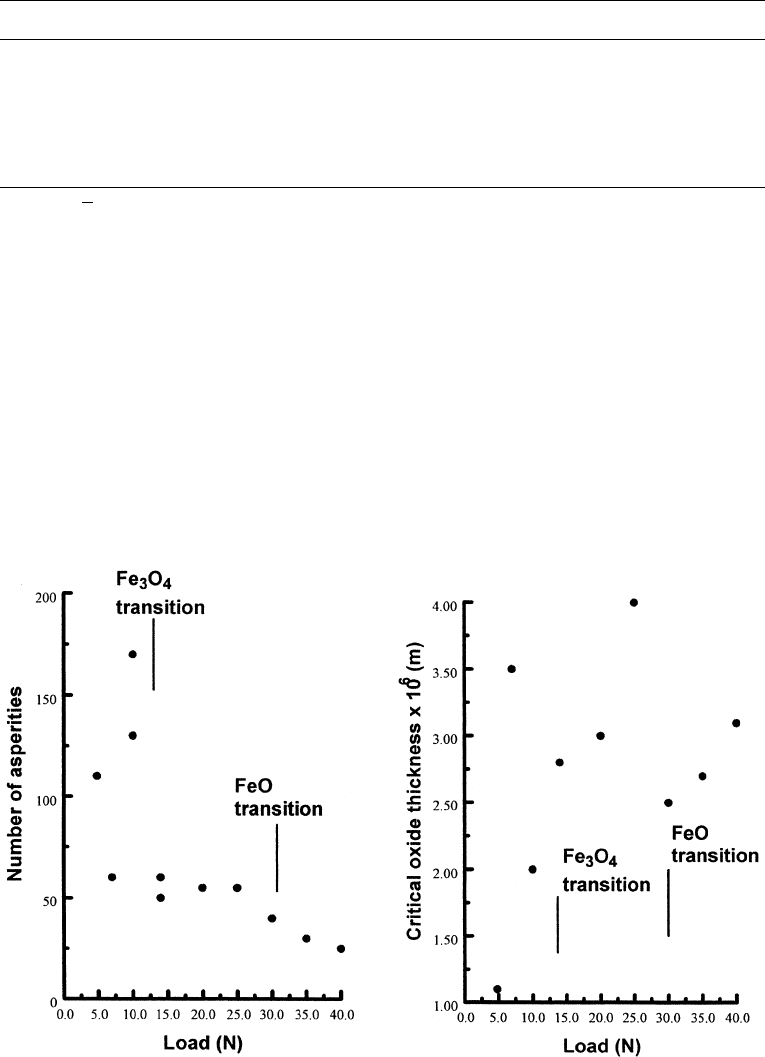
were functions of load (104). This is shown in Fig. 3.47 for one sliding speed. It

can be seen that speed and the region of oxidat ion affect the relationships between these

parameters and load. A similar regression analysis of dry sliding data for EN31 was also

done. These data are shown in Fig. 3.48. In this case, it was found that a correlation

existed between these parameters, T, and the state of oxidation of the surface, that is,

the mixture of Fe

and Fe

. These correlations are shown in Fig. 3.49 (98). These

results imply that n, d

, T and w are interrelated and characteristic of a state of oxidation.

Figure 3.46 Wear rate as a function of load for unlubricated sliding between self-mated steel. The

transitions in oxide formation are also shown. (From Ref. 104, reprinted with permission from

ASME.)

The state of oxidation is determined by the operating conditions and the heat ﬂow char-

acteristics of the interface which is affected by the properties of the oxide. The regression

analysis used in these studies involved the simultaneous satisfaction of wear and heat ﬂow

conditions.

Oxidative wear is primarily a sliding wear mechanism. It generally does not occur

with lubrication. Since this mechanism is related to the chemical reactivity, it is more sig-

niﬁcant with metals than other materials. However, oxidative wear processes have been

found to occur with ceramics, as well (106). It is important to recognize that not all unlu-

bricated sliding situations with metals involve oxidative wear processes. For example, in

Table 3.6 Oxidation Kinetics of Steel Surfaces

Temperature (



C) Oxide b

(kg

(kJ=mole)

T < 45 Fe

208

45 < T < 600 Fe

0.96

600 < T Fe

210

FeO

¼ b



Symbols: Dm, mass oxygen taken up per unit time; R, gas constant.

Determined by regression analysis of wear data.

Source: Ref. 104.

Figure 3.47 Variation in the number of junctions and critical oxide thickness as a function of load

for unlubricated sliding between self-mated steel. The transitions in oxide formation are also shown.

(From Ref. 104, reprinted with permission from ASME.)