Bayro-Corrochano E., Scheuermann G. Geometric Algebra Computing: in Engineering and Computer Science

Подождите немного. Документ загружается.

228 B. Cruz et al.

Table 1 Results of the classiﬁcation phase

Data Set Patterns used in FS Classiﬁcation of FS Classiﬁcation of TS

Iris Plant 15 100% 90%

Iris Plant 25 100% 93.3%

Iris Plant 30 100% 94.6%

Wines 15 90.6% 71.9%

Wines 25 91.1% 80.9%

Wines 30 97.7% 84.8%

was adopted, the Iris Plant Data Base. This data set contains three classes of 50

instances each, where each class refers to a type of iris plant. One class is linearly

separable from the other two; the latter two classes are NOT linearly separable from

each other. Each instance has four numeric, predictive attributes (sepal length, sepal

width, petal length, and petal width).

For the second trial, the Wine Recognition Data Base was used. These data are

the results of a chemical analysis of wines grown in the same region in Italy but

derived from three different cultivations. The analysis determined the quantities of

13 constituents found in each of the three types of wines. This data set contains three

classes of 59, 48, and 71 instances, respectively, where each class refers to a type of

wine. Each instance has 13 continuous attributes.

Both data bases were obtained from [3]. As in the previous section, the func-

tion quadprog of the optimization toolbox of Matlab was used in order to solve the

quadratic programming problem.

15, 25, and 30 instances, respectively, were used to form the Fundamental Set

(FS) for each type of problem. All of the instances were used to form the Test Set

(TS). In the training phase, patterns of each FS were used to build the GAMs. In

the classiﬁcation phase, patterns of the TS were classiﬁed; the results are shown in

Table 1. The ﬁrst column shows the number of patterns used for the learning phase,

and the second and third columns show the percentages of the patterns correctly

classiﬁed using the FS and the TS, respectively. In the case of the GAM from Iris

Plant data set, perfect recall was obtained because the patterns used for the FS are

spherically separable. In the case of the GAM from the Wine data set, perfect re-

call is not obtained because the patterns are not spherically separable. Thus some

patterns of a speciﬁc class may fall outside their respective class sphere.

It can be observed that classiﬁcation rate of the patterns of the TS (for both data

sets) increases when the number of patterns used in the FS increases. When the FS

has more patterns, the corresponding spheres grow, and then more patterns of the

TS could fall inside of the class spheres.

7 Conclusions and Future Work

Geometric Algebra allows one to model situations and to formulate problems in

terms of high-level symbolic expressions. Nevertheless, it is possible to achieve an

Geometric Associative Memories and Their Applications to Pattern Classiﬁcation 229

implementation working in an elementary coordinate system. Of course, in some

cases, it is possible to ﬁnd a solution by purely handling symbolic expressions, but

this is rare for realistic problems.

In this work, a new associative memory model based on Conformal Geometric

Algebra has been described, the Geometric Associative Memory (GAM). The train-

ing phase is done by ﬁnding an optimal sphere with quadratic programming. GAMs

can perfectly operate when the classes are spherically separable.

For classiﬁcation purposes, an inner product between the unclassiﬁed pattern and

the GAM was applied. Then a minimum function is used to obtain the index class.

Numerical and real examples were given to show the potential of the proposal. As

shown, the method can operate both with linearly and nonlinearly separable patterns.

The proposed model can also cope with distorted patterns.

Patterns located on the border of the sphere might not be well classiﬁed. At this

moment, a way to extend the radius of the sphere is been developing. The basic idea

is to change the restrictions of the optimization problem.

Formal conditions under which the proposed model can work were also given

and proven. In particular, the case of the perfect classiﬁcation was presented. A brief

explanation about the functioning of the GAMs against the noise was presented; the

GAMs can cope with noise patterns when the noise version falls inside of the class

sphere.

Nowadays, we are also interested to test our method in more realistic situations

and in comparison (in computing time and performance) between the proposed

model and other geometric classiﬁcation models. We are working too in GAMs

that work with separation surfaces other than spheres, like ellipses, squares, or other

irregular shapes; then, the GAMs can work with nonspherically separable classes.

Acknowledgements The authors thank the National Polytechnic Institute of Mexico (SIP-IPN)

under grants 20090620 and 20091421. Authors also thank the European Union, the European Com-

mission, and CONACyT for the economical support. This paper has been prepared for economical

support of the European Commission under grant FONCICYT 93829. The content of this paper is

an exclusive responsibility of the CIC-IPN, and it cannot be considered that it reﬂects the position

of the European Union. We thank also the reviewers for their comments for the improvement of

this paper.

References

1. Anderson, J.: A simple neural network generating an interactive memory. Math. Biosci. 14,

197–220 (1972)

2. Arena, P., Baglio, S., Fortuna, L., Xibilia, M.: Chaotic time series prediction via quaternionic

multilayer perceptrons. Syst., Man and Cybern., Intell. Syst. for the 21st Century, IEEE Int.

Conf., vol. 2, pp. 1790–1794 (1995)

3. Asuncion, A., Newman, D.: UCI machine learning repository (2007). http://www.ics.uci.edu/

mlearn/MLRepository.html

4. Banarer, V., Perwass, C., Sommer, G.: The hypersphere neuron. 11th Eur. Symp. on Artif.

Neural Netw. Evere, Belgium: d-side publ., pp. 469–474 (2003)

5. Barron, R.: Memorias asociativas y redes neuronales morfologicas para la recuperacion de

patrones. Ph.D, thesis, Mexico, DF: National Institute Politechnic—Center of Computing Re-

search (2006)

230 B. Cruz et al.

6. Barron, R., Cruz, B., Sossa, H., Laguna, G.: Conformal geometric algebra for spherical convex

hull optimization. In: Proc. 3rd Internat. Conf. on Appl. of Geom. Algebras in Comput. Sci.

and Eng., AGACSE 2008 (2008)

7. Bayro, E., Vallejo, R.: Geometric feedforward neural networks and support vector machines.

In: Bayro-Corrochano, E., Sobczyk, G. (eds.) Geometric Algebra with Applications in Science

and Engineering, pp. 309–325. Birkhäuser, Basel (2001)

8. Buchholz, S.: A theory of neural computation with Clifford algebras. Thesis, Kiel: Christian-

Albrechts-Universitat (2005)

9. Buchholz, S., Tachibana, K., Hitzer, E.: Optimal learning rates for Clifford neurons. In: Proc.

of ICANN 2007, Part I. LNCS, vol. 4668, pp. 864–873. Springer, Berlin (2007)

10. Clifford, W.: Applications of Grassmann’s extensive algebra. Am. J. Math. 1(4), 350–358

(1878)

11. Cruz, B., Sossa, H., Barron, R.: A new two level associative memory for efﬁcient pattern

restoration. Neural Process. Lett. 25, 1–16 (2007)

12. Cruz, B., Barron, R., Sossa, H.: Geometric associative memory model with application to

pattern classiﬁcation. In: Proc. 3rd Internat. Conf. on Appl. of Geom. Algebras in Comput.

Sci. and Eng., AGACSE 2008 (2008)

13. Hitzer, E.: Euclidean geometric objects in the Clifford geometric algebra of origin, 3-space,

inﬁnity. Bull. Belg. Math. Soc. 11(5), 653–662 (2004)

14. Hestenes, D., Sobczyk, G.: Clifford Algebra to Geometric Calculus. Springer, Berlin (1984)

15. Hestenes, D.: Old wine in new bottles. In: Bayro-Corrochano, E., Sobczyk, G. (eds.) Geomet-

ric Algebra: A Geometric Approach to Computer Vision, Quantum and Neural Computing,

Robotics, and Engineering, pp. 498–520. Birkhäuser, Basel (2001)

16. Hestenes, D., Li, H., Rockwood, A.: New algebraic tools for classical geometry. In: Som-

mer, G. (ed.) Geometric Computing with Clifford Algebras. vol. 40, pp. 3–23. Springer, Hei-

delberg (2001)

17. Hildebrand, D.: Geometric computing in computer graphics using conformal geometric alge-

bra. Tutorial, TU Darmstadt, Germany: Interact. Graph. Syst. Group (2005)

18. Hopﬁeld, J.: Neural networks and physical systems with emergent collective computational

abilities. Proc. Natl. Acad. Sci. 79, 2554–2558 (1982)

19. Kohonen, T.: Correlation matrix memories. IEEE Trans. Comput. C-21(4), 353–359 (1972)

20. Li, H., Hestenes, D., Rockwood, A.: Generalized homogeneous coordinates for computational

geometry. In: Sommer, G. (ed.) Geometric Computing with Clifford Algebras. vol. 40, pp. 27–

52. Springer, Heidelberg (2001)

21. McCulloch, W., Pitts, W.: A logical calculus of the ideas immanent in nervous activity. Bull.

Math. Biophys. 5, 115–133 (1943)

22. Nakano, K.: Associatron a model or associative memory. IEEE Trans. Syst., Man Cybern 12,

380–388 (1972)

23. Ritter, G., Sussner, P., Diaz-de-Leon, J.: Morphological associative memories. IEEE Trans.

Neural Netw. 9(2), 281–293 (1998)

24. Sossa, H., Barron, R.: New associative model for pattern recall in the presence of mixed noise.

IASTED Fifth Int. Conf. on Signal and Image Process. (SIP 2003), pp. 485–490 (2003)

25. Steinbouch, K.: Die Lernmatrix. Kybernetik 1(1), 26–45 (1961)

26. Sussner, P.: Observations on morphological associative memories and the kernel method. Neu-

rocomputing 31, 167–183 (2003)

27. Yañez, C., Diaz-de-Leon, J.: Introducción a las memorias asociativas. Mexico: Res. in Comp.

Sci. (2003)

Classiﬁcation and Clustering of Spatial Patterns

with Geometric Algebra

Minh Tuan Pham, Kanta Tachibana,

Eckhard M.S. Hitzer, Tomohiro Yoshikawa,

and Takeshi Furuhashi

Abstract In ﬁelds of classiﬁcation and clustering of patterns most conventional

methods of feature extraction do not pay much attention to the geometric properties

of data, even in cases where the data have spatial features. This paper proposes to

use geometric algebra to systematically extract geometric features from data given

in a vector space. We show the results of classiﬁcation of handwritten digits and

those of clustering of consumers’ impression with the proposed method.

1 Introduction

Nowadays classiﬁcation and clustering of patterns are of central importance for dis-

covery of information from enormous amounts of data available in various practical

ﬁelds. An appropriate method to extract features from patterns is needed for good

classiﬁcation and clustering. But so far most conventional methods of feature ex-

traction ignore the geometric properties of data even in the case where the data have

spatial features. For example, when m vectors are measured from an object in three-

dimensional space, conventional methods represent the object by x ∈R

which is

the vector made by arranging m groups of three coordinates of each vector in a row.

However, using only these coordinate values fails to capture geometric relationships

among m vectors, e.g., the coordinate values depend on the deﬁnition of the coordi-

nate system, and inference or classiﬁcation becomes remarkably bad when objects

are measured in a coordinate system different from the one used for learning. Some

conventional methods may extract coordinate-free features, but whether such fea-

tures arise and are adopted depends on experience of the model builder. For example,

some image recognition methods used moment vectors [1, 2] as feature vectors for

learning. The moment vectors are the generalization moments of inertia of each spa-

tial vector, and it is expressed by a linear sum of {x

i,1

i,2

|i =1,...,m;a,b ∈ N},

M.T. Pham (



)

Nagoya University, Furou 1-1, Chikusa, Nagoya, Japan

e-mail: minhtuan@cmplx.cse.nagoya-u.ac.jp

E. Bayro-Corrochano, G. Scheuermann (eds.), Geometric Algebra Computing,

DOI 10.1007/978-1-84996-108-0_12, © Springer-Verlag London Limited 2010

231

232 M.T. Pham et al.

where (x

i,1

i,2

) is the coordinate of vector i. However, the relations between dif-

ferent spatial vectors are not considered in the moment, i.e., the components of

i,1

j,2

|i =j } are not considered at all. So, it is hard to classify data that contain

relations between spatial vectors.

In this study, we use geometric algebra (GA) [3–5] to systematically undertake

various kinds of feature extractions and to improve precision and robustness in clas-

siﬁcation and clustering problems. There are already many successful examples of

its use in, e.g., colored image processing or multidimensional time-series signal pro-

cessing with low-dimensional GAs [6–12]. In addition, GA-valued neural network

learning methods for learning input–output relationships [13] are well studied. In

our proposed method, geometric features extracted with GA can also be used for

learning a distribution and for semi-supervised clustering.

We use geometric features to learn a Gaussian mixture model (GMM) with the

expectation maximization (EM) algorithm [14]. Because each feature extraction de-

rived by the proposed method has its own advantages and disadvantages, we apply

a plural mixture of GMMs for a classiﬁcation problem. As an example of multiclass

classiﬁcation of geometric data, we use a handwritten digit dataset. When classify-

ing new handwritten digits in practice with the learning model, it is natural to expect

that the coordinate system in a real new environment differs from the one used for

obtaining the learning dataset. Therefore, in this paper, we evaluate the classiﬁcation

performance for randomly rotated test data.

As a second application, we analyze a dataset of questionnaire for a newly devel-

oped product. Characteristics of this dataset are:

1. The same m questions are asked for n different objects (usage scenes of the

product).

2. Each respondent answers his/her willingness to buy for either of three different

prices and does not answer for the other prices.

Considering the ﬁrst characteristic, we regard a pattern of answering to the ques-

tions by a respondent as a tuple of m points in an n-dimensional space. This aims

to extract features of n-dimensional shape formed by the m vectors with GA. For

the second characteristic, we utilize harmonic functions [17] for the semi-supervised

learning. In our proposed method, geometric features extracted with GA can be used

for deﬁning a weighted graph over unlabeled and labeled data where the weights

are given in terms of a similarity between respondents. To evaluate the effect of fea-

tures extracted with GA, we examine kernel matrices induced from the geometric

features using kernel alignment [18] between them. This paper reports a result of

semi-supervised clustering of respondents taking geometric properties of question-

naire into consideration.

2Method

This section describes our proposal to extract geometric features from spatial pat-

terns for classiﬁcation and clustering. Our general scheme is based on a description

of shape formed by m-tuple of n-dimensional vectors by GA.

Classiﬁcation and Clustering of Spatial Patterns with Geometric Algebra 233

2.1 Feature Extraction for Geometric Data

An orthonormal basis {e

, e

,...,e

} can be chosen for a real vector space R

.The

GA of R

, denoted by G

, is constructed by an associative and bilinear product of

vectors, the geometric product, which is deﬁned by



1 (i =j),

−e

(i =j).

(1)

GAs are also deﬁned for negative squares e

=−1 of some or all basis vectors. Such

GAs have many applications in computer graphics, robotics, virtual reality, etc. [5].

However, for our purposes, deﬁnition (1) will be sufﬁcient.

The geometric product of linearly independent vectors a

,...,a

(k ≤n) has its

maximum grade term as the k-blade a

∧···∧a

. Linear combinations of k-blades

are called k-vectors, represented by



I ∈I

, where I

={i

...i

| 1 ≤ i

···<i

≤n}.ForG



denotes the set of all k-blades, and G

denotes set of

k-vectors. The geometric product of k vectors yields

...a

∈



⊕···⊕G

k−2

⊕



(odd k),

⊕···⊕G

k−2

⊕



(even k).

(2)

Now we propose a systematic derivation of feature extractions from a series or a

set of spatial vectors ξ ={p

∈R

,l =1,...,m}. Our method is to extract the scalar

part of products of k-vector data that encode the different features.

First, assuming that ξ is a series of n-dimensional vectors, n



+1 feature extrac-

tions are derived, where n



=min{n, m}.Fork =1,...,n



(ξ) =



...p

l+k−1

−1



,I ∈I

,l =1,...,m−k +1



∈R

(m−k+1)|I

, (3)

where · denotes the operator that selects the scalar part, |I

| is the number of

combinations of k elements from n elements, and e

−1

is the inverse of e

.ForI =

...i

, e

−1

...e

. When k>n



, this means that ∀l ∈{1,...,m−k +1},

p

...p

l+k−1

−1

=0. This feature is not possible in the case of classiﬁcation prob-

lem or clustering. We further deﬁne

(ξ) =



p

l+1

,l =1,...,m−1



∈R

m−1

. (4)

Next, assuming that ξ is a set of vectors, n



+1 feature extractions can also be

derived in the same way:

(ξ) =



···p

−1



,I ∈I



∈R

(

)|I

, (5)

(ξ) =



p





∈R

(

+m)

. (6)

The dimension of the feature space becomes different from the case where ξ is a

series.

234 M.T. Pham et al.

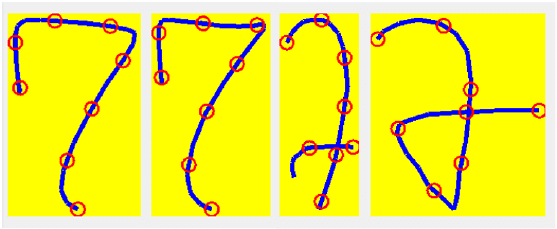
Fig. 1 Examples of handwritten digit “7”

We denote by f

a feature vector extracted by a feature extraction f

. f

is the

scalar part in the geometric product of two vectors chosen from n vectors. f

con-

sists of the coefﬁcient of k-blade in the geometric product of k vectors chosen from

n vectors. f

and f

do not depend on the measurement coordinate system.

Below we show several feature extractions for the case of handwritten digit data

of the UCI Machine Learning Repository [15] and the case of questionnaire data.

Each of the digit data is given by eight points ξ ={p

,...,p

}, measured by

dividing the handwritten curves in equally long curve segments. A two-dimensional

point is given by p

with



l=1



l=1

=0. Using GA, various

kinds of feature extraction can be undertaken systematically. Figure 1 shows some

examples of the handwritten digit “7”. They are shown with straight line segments,

different from the real curved trajectories of a pen.

The simplest feature extraction f

, which is also used in conventional methods,

(ξ) =



−1





−1



,...,



−1





−1



=[p

·e

, p

·e

,...,p

·e

, p

·e

]

=[x

,...,x

]∈R

. (7)

A second feature extraction f

uses the directed magnitudes of outer products of

consecutive points:

(ξ) =



−1



,...,



−1



=[x

−x

,...,x

−x

]∈R

. (8)

A third feature extraction f

uses the inner product of consecutive points:

(ξ) =



p

,...,p





=[x

,...,x

]∈R

. (9)

Each respondent gave evaluation values to the same ten questions for six ob-

jects. We therefore regard a ﬁlled out questionnaire as m(=10) points in an n(=6)-

Classiﬁcation and Clustering of Spatial Patterns with Geometric Algebra 235

dimensional space: ξ ={p

,...,p

}, p



l,i

with x

l,i

∈{−2, −1, 0, 1, 2}.

Using GA, various kinds of feature extractions can be undertaken systematically. In

this paper, we use three kinds of features extracted from ξ with GA.

The simplest feature extraction f

, which is coordinate value, also used in con-

ventional methods, is

(ξ) =



−1



,...,



−1



,...,



−1



,...,



−1



=[x

1,1

1,2

,...,x

10,5

10,6

]∈R

. (10)

A second feature extraction f

uses the inner product of two points:

(ξ) =



p

, p

,...,p





∈R

. (11)

If two questions are correlated for six objects, then the corresponding element of f

becomes large.

Finally, a third feature extraction f

uses outer product of two points:

(ξ) =



−1



,...,



−1



,...,



−1



,...,



−1



∈R

675

. (12)

Each |I

| elements of f

express independence of two questions and the direction

of hyper-plane spanned by the two questions in the six-dimensional space. If two

questions are uncorrelated, then the corresponding element becomes large.

2.2 Distribution Learning and Its Mixture for Classiﬁcation

A GMM is useful to approximate a data distribution in a data space. A GMM is

characterized by parameters Θ ={β

,μ

,Σ

}, where β

, μ

, and Σ

are the mix-

ture ratio, the mean vector, and the variance covariance matrix of the j th Gaussian,

respectively. The output is

p(ξ |Θ) =



j=1



f(ξ)−μ

;Σ



, (13)

where N

(·;·) is the d-dimensional Gaussian distribution function with center ﬁxed

at the origin.

To train M Gaussians with given incomplete data X ={x

=f(ξ

) |1 ≤i ≤N},

the EM algorithm [14] is often utilized. The algorithm identiﬁes both parameters Θ

and latent variables Z ={z

∈{0, 1}|1 ≤ j ≤ M}.Thez

are random variables

with z

=1 indicating that the individual datum x

belongs to the j th of M Gaus-

sian distributions. Thus



j=1

P(z

) =1. The EM algorithm repeats the E-step and

236 M.T. Pham et al.

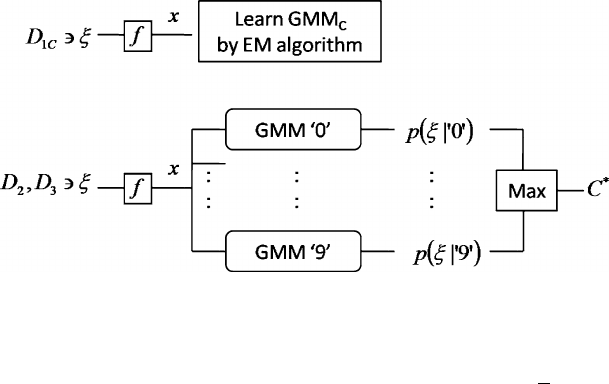
Fig. 2 Flow of multiclass classiﬁcation. The top diagram shows the training of the GMM for class

C ∈{‘0’,...,‘9’}.TheD

denotes a subset of training samples with label C.Thef :ξ →x

shows feature extraction. Either of {f

} is chosen as f . The bottom diagram shows esti-

mation by the learned GMMs. The same f chosen for training is used here. The GMM

outputs

p(ξ | C). The ﬁnal estimation is C

∗

= argmax

p(ξ | C)P (C),whereP(C) =

is the prior

distribution. The set D

consists of independent test data

the M-step until P(Z)and Θ converge. The E-step updates the probabilities of Z ac-

cording to Bayes’ theorem P(Z |X, Θ) ∝p(X |Z,Θ). The M-step updates the pa-

rameters Θ of the Gaussians to maximize the likelihood l(Θ,X,Z) =p(X |Z,Θ).

A major drawback of the GMM is its large number of free parameters whose

order is O(Md

). Moreover, when the correlation between any pair of features is

close to 1, the calculation of the inverse matrix is numerically unstable. So, the

GMM becomes unable to compute the correct probability distribution. To remedy

this, Tipping and Bishop [16] proposed to use only the eigencomponents with the

largest q eigenvalues, where q is a preset value of a Gaussian distribution. For fur-

ther better approximation of a probability distribution, Meinicke and Ritter [19]

proposed to use only the eigencomponents of Gaussian distributions that are larger

than a certain cutoff. The cutoff eigenvalue is set at λ

−

= αλ

max

, where α ∈ (0, 1]

is a hyperparameter, and λ

max

is the largest eigenvalue of the variance covariance

matrix of incomplete data X. This means that we develop (13) as follows:

p(x |Θ) =



j=1



k=1



(x −μ

) ·v

;λ



≈



j=1





k=1



(x −μ

) ·v

;λ







(x −μ

)

−

;λ

−



d−q

, (14)

where λ

is the kth largest eigenvalue of the j th Gaussian distribution, and v

the corresponding eigenvector. Because k ≤q

is equivalent to λ

>λ

−

, the bracket

(x − μ

)

−

=(x − μ

) · v

is the length of the component which is perpendicular

to all of the q

eigenvectors with the largest eigenvalues.

Classiﬁcation and Clustering of Spatial Patterns with Geometric Algebra 237

Fig. 3 Mixture of GMMs. Three GMMs via different feature extractions are mixed to yield output

p(ξ |C)

The ﬂow of training and estimation of handwritten digit classiﬁcation, as an ex-

ample of multiclass classiﬁcation, is shown in Fig. 2.TheM and α for each GMM

are decided by validation with dataset D

Each feature extraction derived with GA has advantages and disadvantages. A

big merit of adopting learning of distributions rather than learning of input–output

relations is that the learned distributions allow us to obtain reliable inference by

mixing plural weak learners. In this study, we therefore use a mixture of GMMs.

Inferences are mixed as

p(ξ |C) =



k=0



(ξ) |C



. (15)

Figure 3 shows the mixture of different GMMs. Inferences via different feature

extractions are mixed to produce the output p(ξ |C).

2.3 GA Kernel and Alignment and Semi-Supervised Learning

for Clustering

For feature extractions f

,k=0, 1, 2, with GA, we deﬁne a similarity between two

instances i, j ∈{1,...,p} as

ij ;k

=exp



−

f

(ξ

) −f

(ξ

)



, (16)

where ·is the Euclidean distance in the feature space, and a parameter σ

decided by Zhu et al. [17] as described below. The kernel matrix W

=[w

ij ;k

] is a

symmetric matrix with p rows and p columns.

In this study, we combine three kinds of feature extractions to cluster instances.

The effect of combining two feature extractions becomes small if their kernel ma-

trices are aligned. The alignment [18] between two kernel matrices is deﬁned as

A(W

) =



i,j

w

ij ;k

w

ij ;l

∈(0, 1], (17)