Bayro-Corrochano E., Scheuermann G. Geometric Algebra Computing: in Engineering and Computer Science

Подождите немного. Документ загружается.

QWT: Retrospective and New Applications

Yi Xu, Xiaokang Yang, Li Song,

Leonardo Traversoni, and Wei Lu

Abstract Quaternion wavelet transform (QWT) achieves much attention in recent

years as a new image analysis tool. In most cases, it is an extension of the real

wavelet transform and complex wavelet transform (CWT) by using the quaternion

algebra and the 2D Hilbert transform of ﬁlter theory, where analytic signal rep-

resentation is desirable to retrieve phase-magnitude description of intrinsically 2D

geometric structures in a grayscale image. In the context of color image process-

ing, however, it is adapted to analyze the image pattern and color information as

a whole unit by mapping sequential color pixels to a quaternion-valued vector sig-

nal. This paper provides a retrospective of QWT and investigates its potential use

in the domain of image registration, image fusion, and color image recognition.

It is indicated that it is important for QWT to induce the mechanism of adaptive

scale representation of geometric features, which is further clariﬁed through two

application instances of uncalibrated stereo matching and optical ﬂow estimation.

Moreover, quaternionic phase congruency model is deﬁned based on analytic signal

representation so as to operate as an invariant feature detector for image registra-

tion. To achieve better localization of edges and textures in image fusion task, we

incorporate directional ﬁlter bank (DFB) into the quaternion wavelet decomposition

scheme to greatly enhance the direction selectivity and anisotropy of QWT. Finally,

the strong potential use of QWT in color image recognition is materialized in a

chromatic face recognition system by establishing invariant color features. Exten-

sive experimental results are presented to highlight the exciting properties of QWT.

1 Introduction

Quaternion wavelet transform (QWT) attracts increasing research interests recently

as a new analysis tool for various image processing tasks. It is usually formulated as

L. Traversoni (



)

Ciencias Básicas e Ingenieria, Univ. Autonoma Met. (Iztapalapa), 09340 Mexico, Mexico

e-mail: ltd@xanum.uam.mx

E. Bayro-Corrochano, G. Scheuermann (eds.), Geometric Algebra Computing,

DOI 10.1007/978-1-84996-108-0_13, © Springer-Verlag London Limited 2010

249

250 Y. Xu et al.

an extension of the real wavelet transform and complex wavelet transform (CWT) by

using the quaternion algebra and the 2D Hilbert transform of ﬁlter theory. Typically,

analytic signal representation is desirable to retrieve phase-magnitude description

of intrinsically 2D geometric structures in a scalar image. The amplitude compo-

nent reveals the energy of the ﬁlter response and therefore serves for the detection

of events, while the phase component uncovers the type of the detected event and

encodes the relative location of image structures [1]. In the applications involved

in comparison of series of images, such as optical ﬂow [1, 2] and stereo matching

[3, 4], the phases of quaternion wavelet transformed image are very important to

provide essential features and inherent 2D shift clues at corresponding points. In

addition, the conﬁdence map of the movement measurement can be built according

to the complementary amplitude spectrum [4].

Meanwhile, some preliminary research works provide an insight of the use of

QWT in vector signal representation, such as the spectrum analysis for quaternion-

valued color image [5] and color pattern estimation [6, 7]. Compared with the tra-

ditional color image ﬁltering techniques, which are commonly based on separate

processing of the color components, quaternion ﬁlters can depict a color pixel as a

whole unit, namely pure quaternion, and naturally compute transformation in three-

dimensional color/vector space. This operation would make full use of inter-channel

color information and efﬁciently suppress the artifacts. The pioneer work of Ell uti-

lized quaternion Fourier transform (QFT) to treat color as a single entity and achieve

higher color information accuracy [5]. To improve the strength of local quaternion

ﬁltering in color space, some face recognition systems deﬁned a family of quater-

nion Gabors to extract local color features for high face recognition accuracy [6, 7].

Philippe Carré and Patrice Denis built a color quaternionic ﬁlter bank called the

color Shannon wavelet based on a windowing process in the quaternionic Fourier

space and established joint spatio-frequential representation of color images [8].

Aforementioned discussion demonstrates that QWT is a very useful image analy-

sis tool and could be applied in extensive scalar/vector image processing tasks. This

paper is motivated to give a suggestive reference for the use of QWT. It attempts

to summarize the lessons from the QWT development experience and explores the

potential applications of QWT. The remainder parts of this paper are structured as

follows. Section 2 surveys the evolution of QWT and presents the basic principles of

quaternion wavelet construction for analytic signal analysis. Section 3 indicates that

the mechanism of adaptive scale representation of geometric features is important

for image analysis, which is testiﬁed in two application instances of uncalibrated

stereo matching and optical ﬂow estimation. Sections 4 and 5 switch the focus to the

potential use of QWT in two new applications, namely image registration and im-

age fusion. As for image registration application, the quaternionic phase congruency

model is deﬁned to give an invariant feature detector in scale space. The accordingly

extracted features are matched to robustly estimate the image afﬁne transformation

in registration task. With regard to image fusion application, we incorporate direc-

tional ﬁlter bank (DFB) into the quaternion wavelet decomposition scheme to en-

hance the direction selectivity and anisotropy of QWT. Consequently, the modiﬁed

QWT scheme could provide a better representation of edges and textures. Section 6

QWT: Retrospective and New Applications 251

materializes the strong potential use of QWT in color image recognition by estab-

lishing invariant color features in a chromatic face recognition system. Section 7 is

devoted to conclusions and future work.

2 Evolution of Qwt and Principles of Quaternion Wavelet

Construction

The notion of quaternion was introduced by Hamilton in 1843 [9]. Recently, a new

research branch called quaternion Fourier transform (QFT) has been developed

based on quaternion algebra and is important for quaternion linear time-invariant

system analysis [10, 11]. In analogue to complex Fourier space, the earliest deﬁni-

tion of QFT is the two-side form as follows [1]:

(u, v) =



∞

−∞



∞

−∞

−iux

f(x,y)e

−jvy

dx dy. (1)

In fact, there are many variants of QFT, e.g., the right-side QFT

(u, v) =



∞

−∞



∞

−∞

f(x,y)e

−μ(ux+vy)

dx dy (2)

where μ is a unit pure quaternion. Similar to 1D wavelets, the existing quaternion

wavelets have been constructed as a family of functions based on windowing process

in the quaternionic Fourier space [1–4, 8].

2.1 Evolution of QWT

Unlike Fourier basis functions, the locality of quaternion wavelet basis leads to

sparse representation of singularity-rich signals by compacting the signal energy

into a small number of coefﬁcients. The generated spatial features associated with a

given scale and spatial support form the foundation for the analysis of linear time-

varying system, commonly the various procedures of local image analysis and esti-

mation.

One of the ﬁrst applications of quaternion wavelet is Bülow’s work [1]. He de-

ﬁned the concept of quaternion Gabor, i.e., a Gaussian windowed basis function of

the QFT, for use with scalar images. Nowadays, quaternion Gabors are the most

commonly used quaternion wavelets and can be obtained from tensor product ex-

tension of complex Gabors in quaternion domain:

Quaternion Gabor:

(x, u,m)=

2πm

−0.5(

mσ

)

−0.5(

mσ

)

−i2πux

−j2πvy

, (3)

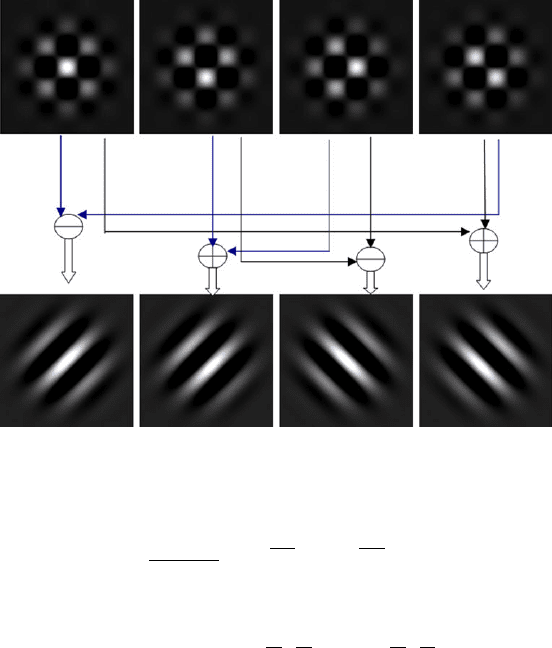
252 Y. Xu et al.

Fig. 1 Two complex Gabors (bottom) contained in a quaternion Gabor (top)

Complex Gabor:

G(x, u,m)=

2πm

−0.5(

mσ

)

−0.5(

mσ

)

−i2π(ux+vy)

(4)

where u =(u, v)

is the radial center frequency of the ﬁlter, and the Gaussian enve-

lope is truncated by the window x ∈[−

], y ∈[−

]. Parameter m is the

number of wavelength included in the window, and σ

denotes the fraction of the

window size that corresponds to one standard deviation of the Gaussian envelope

along x,y directions. Since 99.7% of the envelope is located within three standard

deviations from the origin, usually we select σ

=1/6. Fixing parameter and vary-

ing radial center frequency u, we get a family of constant-octave quaternion Gabors.

From (3) and (4) it is noted that two quaternion bases i and j (i

=−1

and i ·j =k) replace the single complex root i in the complex Gabor ﬁlter. Therefore

the quaternion Gabor in (3) contains the complex Gabor in (4) and can generate an-

other complex Gabor, which is the complementary part to represent a real 2D signal

in the complex Fourier frequency domain, as shown in Fig. 1. The use of quaternion

Gabors in biometrics is justiﬁed since the proﬁles of cortical receptive were found

to strongly resemble the impulse responses of complex Gabors. Meanwhile, one can

deduce that quaternion Gabors share with their complex counterparts the property

of being jointly optimally localized in the spatial and frequency domains [1].

Similar to complex Gabor, a quaternion Gabor has side-slopes in negative fre-

quency quadrants. In addition, a typical quaternion Gabor image analysis is nonin-

vertible and expensive to compute due to the Fourier kernel. Some researchers built

quaternion wavelets from tensor products of Kinsbury’s q-shift Dual-Tree complex

QWT: Retrospective and New Applications 253

Fig. 2 Three quaternion wavelets built from Dual-Tree complex wavelet [12], capturing horizon-

tal, vertical, and diagonal subbands respectively from row (a)torow(c)[3]. (From left to right at

each row: the real part, three imaginary parts, and the quaternion magnitude)

Fig. 3 Three quaternion wavelets built from biorthogonal wavelet basis [13] based on quaternion

algebra and Hilbert transform, capturing horizontal, vertical, and diagonal subbands respectively

from row (a)torow(c). (From left to right at each row: the real part, three imaginary parts, and

the quaternion magnitude) [4]

wavelets [3] or from biorthogonal wavelet basis based on the quaternion algebra and

2D Hilbert transform [4]. These quaternion wavelets have been constructed through

ﬁnite impulse response (FIR) ﬁlter banks and thus have a fast invertible implementa-

254 Y. Xu et al.

tion.

Moreover, these quaternion wavelets have the general formulation as a Hilbert

quadruple:

(x, y) = φ(x)ψ(y) +iφ

(x)ψ(y) +jφ(x)ψ

(y) +kφ

(x)ψ

(y), (5)

(x, y) = ψ(x)φ(y) +iψ

(x)φ(y) +j ψ(x)φ

(y) +kψ

(x)φ

(y), (6)

(x, y) = ψ(x)ψ(y)+iψ

(x)ψ(y) +jψ(x)ψ

(y) +kψ

(x)ψ

(y). (7)

In (5)–(7), φ and ψ represent the low-pass and high-pass ﬁlter pair. Subscript H

denotes the 1D Hilbert transform along the given axis. Therefore the quaternion

wavelets Ψ

,Ψ

respectively capture the horizontal, vertical, and diagonal sub-

bands of the input 2D scalar signal.

In terms of analytic signal construction, QWT is an extension of the real wavelet

transform and complex wavelet transform (CWT) by using the quaternion alge-

bra and the 2D Hilbert transform of ﬁlter theory. The concept of the analytic sig-

nal is important in signal theory and introduced in 1946 by Gabor [14]. It makes

the instantaneous amplitude and phase of local signal directly accessible. As the

strengthening extension of CWT, QWT preserves the properties of CWT and adds

new features by extending local signal phase from 1D complex phase to 2D quater-

nionic phase. QWT can realize the analysis of intrinsically 2D features (corner-like).

In contrast, CWT provides a powerful tool in intrinsically 1D features (edge-like)

analysis, while real wavelet transform cannot be exactly analytic. There were four

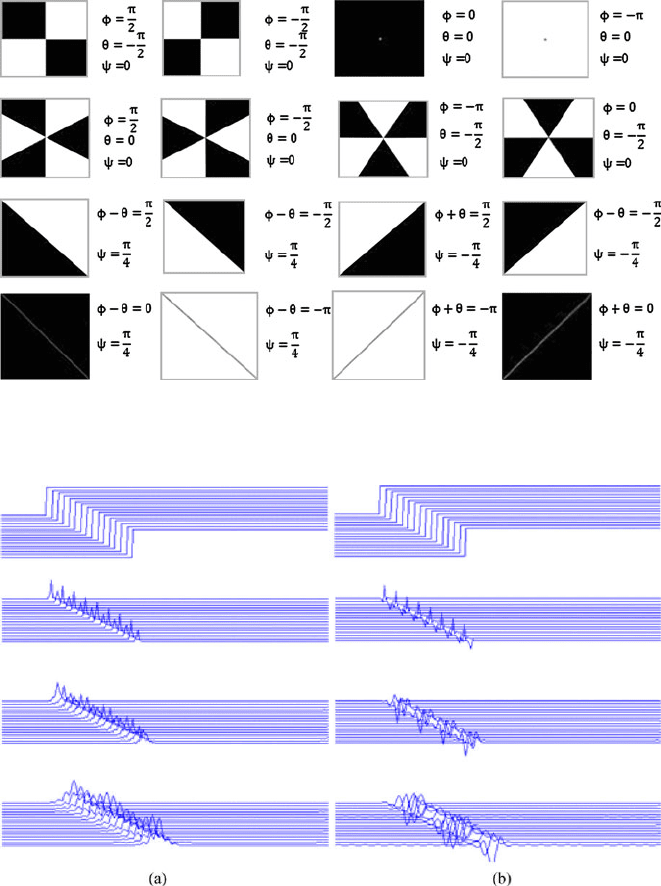
fundamental local structures which could be distinguished from the 1D local phase,

while we can ﬁnd sixteen such structures using the 2D local phase, as compared in

Figs. 4 and 5, where the phase value is determined by the signal and the ﬁlter.

2.2 Principles of Quaternion Wavelet Construction

In the existing works, researchers have paid much attention to the particular use of

quaternion wavelets and the comparison of QWT with DWT and CWT [2, 3]. The

principles of quaternion wavelet construction are somewhat fragmentary to present

in these works. To seek for such a guideline, we would investigate the desirable

properties of the quaternion wavelets in this section.

Linear-Phase and Shift-Invariance Property

It is noted that the linear-phase property of quaternion wavelets is important for

analytic signal representation, and thus no phase compensation is needed in multi-

scale signal decomposition. Besides the most common quaternion Gabors, the tensor

Invertible quaternion wavelet transform (QWT) for quaternion-valued color images is still an open

problem. Section 2 discusses the invertible QWT for scalar images.

The ﬁlter’s shape should match the local variation of the image structures.

QWT: Retrospective and New Applications 255

Fig. 4 Four fundamental 1D local structures and the local complex phases φ evaluated at the

central points

products of linear-phase complex wavelets are usually exploited to build quaternion

wavelets [3, 4]. To capture geometric image features nonoscillatorily, one impor-

tant property of the ﬁlter is that a shift in the time domain should cause no change

in the magnitude spectrum. As an instance to demonstrate the importance of shift-

invariance property, Fig. 6 shows two examples of 1D shifted step responses. It is

noted in (b) that the magnitude of DWT varies signiﬁcantly across time-scale do-

main. The smoothly varied response in (a) indicates the near shift-invariance of

Dual-tree CWT. Similarly, this is also a fundamental assumption for supporting

QWT to resolve those problems involved in comparison of time-variant signals.

Hilbert Quadruple with no DC Response

Four real 2D functions f

,η∈{1, 2, 3, 4}, are called a Hilbert quadruple if



)





)





)



, (8)

256 Y. Xu et al.

Fig. 5 Sixteen fundamental 2D structures and the local quaternionic phases (φ, θ, ψ)

evaluated

at the central points

Fig. 6 (a) Magnitude of 1D shifted step response of Dual-Tree CWT at three successive scales.

(b) Magnitude of 1D shifted step response of the real part of Dual-Tree CWT at three successive

scales

for some permutation of pairwise different k,λ,μ,v ∈{1, 2, 3, 4}, where

=f +if

+jf

+kf

. (9)

QWT: Retrospective and New Applications 257

Operators I(·), J (·), K(·) in (8) respectively extract the three imaginary parts of

the quaternion analytic signal (f

)

that are in turn related to quaternion units i, j, k.

Subscripts Hi

, Hi

in (9) respectively represent the partial Hilbert transform along

x-axis and y-axis, while Hi

denotes the total Hilbert transform in x–y coordinates.

To constitute a bandpass analytic signal, we could use the following conﬁguration:

=Ψ

⊗f =(Ψ +iΨ

+jΨ

+kΨ

) ⊗f. (10)

Due to the commutability of convolution operation ⊗and Hilbert transform, we can

ﬁrst build a quaternion wavelet from real-valued ﬁlters through Hilbert transform

and then construct an analytic signal using convolution operator. The resultant ana-

lytic signal is supported only on the upper right quadrant (u ≥0,v ≥0). In addition,

no DC response is expected in the ﬁltering output. Because of the substantial power

in natural signals at low frequencies, this DC sensitivity often introduces a positive

bias in the real part of the response. This is the main reason why most of authors

select the Gabors with small bandwidth (usually less than one octave) in 1D analytic

signal construction.

Short-Length Filters with Good Localization in Space–Frequency Domain

It is generally accepted that the measurement of geometric image structures should

require only local support in time–frequency domain. Quaternion Gabor ﬁlters are

appropriate when one is interested in local spectral properties of a signal since they

fulﬁll the uncertainty relation as an equality [1]. However, they are irreversible and

usually require heavy computations, especially for the calculation of the quaternion

Fourier transform. As a substitute for the quaternion Gabors, the methods in [3, 4]

formed pixel-wise quaternion wavelets by imposing Hilbert transform respectively

on q-shift orthonormal wavelets and biorthogonal wavelets. These relatively short

ﬁlters would accelerate the measurement of geometric image structures. In the fol-

lowing experiments, this kind of quaternion wavelets is used to extract multiscale

2D phase structures.

3 The Mechanism of Adaptive Scale Representation in QWT

Current works have proved that the local quaternion phase is equivariant with the 2D

spatial position in the scalar image [1, 2]. Thus it is possible to estimate the 2D dis-

parity or optical ﬂow ﬁeld based on the local quaternionic phases [3, 4]. Usually, the

phase-difference model is utilized to implement such tasks [1–3]. The main merit

of the phase use is that the measurement is insensitive to illumination variations and

geometric distortions [15]. However, most of existing phase-based matching meth-

ods have not dealt well with the issue of the inherent phase singularity. At the points

where the amplitude falls to zero, phases are undeﬁned, and thus disparity/optical

ﬂow estimation is unreliable. In the following content, we would point out that the